数制与码制(听课笔记)

数制与码制数制（1）进位制：多位数码每一位的构成以及从低位到高位的进位规则。

（2）基数：在该进位制中可能用到的数码个数。

（3）位权：进位制的数中，每一位数码相应乘上一个固定的幂，表示大小，这个固定的幂就是位权。

一、十进制计数法（D ）数码为：0~9 基数是10运算规律：逢十进一，即9 + 1 = 10十进制数的权展开形式：如：012310105105105105)555(⨯+⨯+⨯+⨯=二、二进制计数法（B ）数码为：0和1 基数是2运算规律：逢二进一，即1 + 1 = 10二进制数的权展开形式：如：2101222120212021)01.101(--⨯+⨯+⨯+⨯+⨯=三、八进制计数法（O ）数码为：0~7 基数是8运算规律：逢八进一，即7 + 1 = 10八进制数的权展开形式：如：2101288480878082)04.207(--⨯+⨯+⨯+⨯+⨯=四、十六进制计数法（H ）数码为：0~9和A~F 基数是16 运算规律：逢十六进一，即F + 1 = 10十六进制数的权展开形式：如：1011616101681613).8(-⨯+⨯+⨯=A D数制的转换将N 进制数按权展开，即可转换为十进制数。

二、八进制数转换① 二进制 八进制：由小数点开始，把每三位二进制数分成一组，不够的补零，每组则对应一位八进制数。

如：001｜101｜010｜.010 8)2.152(01.1101010== 001｜110 8)16(01110==② 二进制 八进制：由小数点开始，将每位八进制数用三位二进制数表示。

如：28)001111110()176(= 其中，八进制数1所对应的二进制数是001；八进制数7所对应的二进制数是111；八进制数6所对应的二进制数是110。

28)010110.011111100()26.374(= 其中，八进制数3所对应的二进制数是011；八进制数7所对应的二进制数是111；八进制数4所对应的二进制数是100；八进制数2所对应的二进制数是010；八进制数6所对应的二进制数是110。

单片机中的数制码制和数据一．十进制数(D)
人类日常生活中使用的计数制。

共10个数码符号（0，1，2，3，4，5，6，7，8，9）
基数 10（分析二进制数，该数为十进制）
权，以10为底的幂次方
特点，逢10进1
二．二进制数(B)
计算机及数码产品中使用的计数制。

共2个数码符号（0，1）
基数 2（分析二进制数，该数为十进制）
权，以2为底的幂次方
特点，逢2进1
表示方法：（1010110）2或 1010110B
三．十六进制(H)
本质上是二进制的一种缩写，方便使用和计数。

共16个数码符号（0，1，2，3，4，5，6，7，8，9，A，B，C，D，E，F）基数 16（分析十六进制数，该数为十进制）
权，以16为底的幂次方
特点，逢16进1
表示方法：（1A2B）16 或 1A2BH
四．数制间的转换
1．二进制、十六进制转十进制
方法: 权展开式
例：将二进制数1010110B转换成十进制数。

例：将十六进制数1A2BH转换成十进制数。

2．十进制转二进制
方法: 除以2倒取余
例：将十进制数86转换成二进制数。

3．十进制转十六进制
方法: 除以16倒取余
例：将十进制数6699转换成十六进制数。

1．二进制转十六进制
方法: 四位合一法
例：将二进制数1010110B转换成十六进制数。

2．十六进制转二进制
方法: 一位分四法
例：将十六进制数据1A2BH转换成二进制数。

五．进制数对照表。

数电知识点汇总一、数制与编码。

1. 数制。

- 二进制：由0和1组成，逢2进1。

在数字电路中，因为晶体管的导通和截止、电平的高和低等都可以很方便地用0和1表示，所以二进制是数字电路的基础数制。

例如，(1011)₂ = 1×2³+0×2² + 1×2¹+1×2⁰ = 8 + 0+2 + 1=(11)₁₀。

- 十进制：人们日常生活中最常用的数制，由0 - 9组成，逢10进1。

- 十六进制：由0 - 9、A - F组成，逢16进1。

十六进制常用于表示二进制数的简化形式，因为4位二进制数可以用1位十六进制数表示。

例如，(1101 1010)₂=(DA)₁₆。

- 数制转换。

- 二进制转十进制：按位权展开相加。

- 十进制转二进制：整数部分采用除2取余法，小数部分采用乘2取整法。

- 二进制与十六进制转换：4位二进制数对应1位十六进制数。

将二进制数从右向左每4位一组，不足4位的在左边补0，然后将每组二进制数转换为对应的十六进制数；反之，将十六进制数的每一位转换为4位二进制数。

2. 编码。

- BCD码（Binary - Coded Decimal）：用4位二进制数来表示1位十进制数。

常见的有8421 BCD码，例如十进制数9的8421 BCD码为(1001)。

- 格雷码（Gray Code）：相邻的两个代码之间只有一位不同。

在数字系统中，当数据按照格雷码的顺序变化时，可以减少电路中的瞬态干扰。

例如，3位格雷码的顺序为000、001、011、010、110、111、101、100。

二、逻辑代数基础。

1. 基本逻辑运算。

- 与运算（AND）：逻辑表达式为Y = A·B（也可写成Y = AB），当A和B都为1时，Y才为1，否则Y为0。

在电路中可以用串联开关来类比与运算。

- 或运算（OR）：逻辑表达式为Y = A + B，当A和B中至少有一个为1时，Y为1，只有A和B都为0时，Y为0。

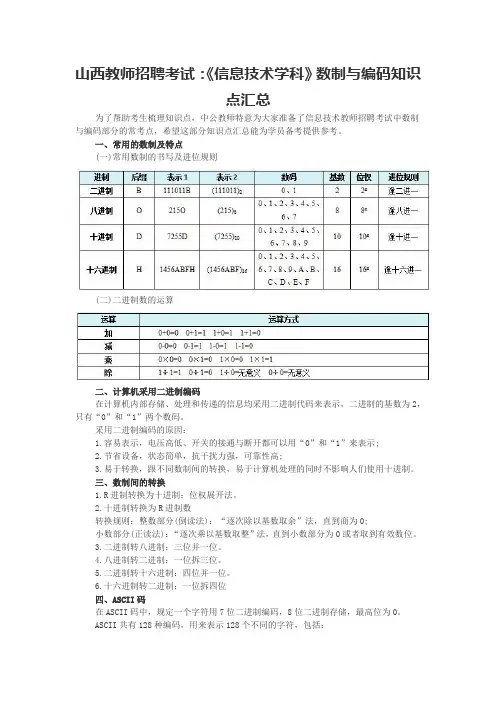
山西教师招聘考试：《信息技术学科》数制与编码知识点汇总为了帮助考生梳理知识点，中公教师特意为大家准备了信息技术教师招聘考试中数制与编码部分的常考点，希望这部分知识点汇总能为学员备考提供参考。

一、常用的数制及特点(一)常用数制的书写及进位规则(二)二进制数的运算二、计算机采用二进制编码在计算机内部存储、处理和传递的信息均采用二进制代码来表示，二进制的基数为2，只有“0”和“1”两个数码。

采用二进制编码的原因：1.容易表示，电压高低、开关的接通与断开都可以用“0”和“1”来表示;2.节省设备，状态简单，抗干扰力强，可靠性高;3.易于转换，跟不同数制间的转换，易于计算机处理的同时不影响人们使用十进制。

三、数制间的转换1.R进制转换为十进制：位权展开法。

2.十进制转换为R进制数转换规则：整数部分(倒读法)：“逐次除以基数取余”法，直到商为0;小数部分(正读法)：“逐次乘以基数取整”法，直到小数部分为0或者取到有效数位。

3.二进制转八进制：三位并一位。

4.八进制转二进制：一位拆三位。

5.二进制转十六进制：四位并一位。

6.十六进制转二进制：一位拆四位四、ASCII码在ASCII码中，规定一个字符用7位二进制编码，8位二进制存储，最高位为0。

ASCII共有128种编码，用来表示128个不同的字符，包括：五、汉字编码1.汉字输入码常见的有智能ABC、五笔字型码、搜狗输入法等。

2.汉字机内码常见的机内码有GB码、GBK码、BIG-5码等。

3.字形码字形码在显示或打印输出汉字时产生的字形，这种编码是通过点阵来实现的。

全部的字形码都放在汉字字库里。

根据对汉字质量要求不同，常用的点阵有16×16，24×24，32×32及48×48。

每个点在存储器中用一个二进制数存储，用“0”、“1”分别表示“白”、“黑”。

根据点阵大小可计算出一个汉字所需的存储空间。

例如，汉字“大”采用16*16的字形码，在计算机中存储需要16*16/8=32个字节。

数电考研阎石《数字电子技术基础》考研真题与复习笔记第一部分考研真题精选第1章数制和码制一、选择题在以下代码中，是无权码的有（）。

[北京邮电大学2015研]A．8421BCD码B．5421BCD码C．余三码D．格雷码【答案】CD查看答案【解析】编码可分为有权码和无权码，两者的区别在于每一位是否有权值。

有权码的每一位都有具体的权值，常见的有8421BCD码、5421BCD码等；无权码的每一位不具有权值，整个代码仅代表一个数值。

二、填空题1（10100011.11）2＝（）10＝（）8421BCD。

[电子科技大学2009研] 【答案】163.75；000101100011.01110101查看答案【解析】二进制转换为十进制时，按公式D＝∑k i×2i求和即可，再由十进制数的每位数对应写出8421BCD码。

2数（39.875）10的二进制数为（），十六进制数为（）。

[重庆大学2014研]【答案】100111.111；27.E查看答案【解析】将十进制数转化为二进制数时，整数部分除以2取余，小数部分乘以2取整，得到（39.875）10＝（100111.111）2。

4位二进制数有16个状态，不够4位的，若为整数位则前补零，若为小数位则后补零，即（100111.111）2＝（0010 0111.1110）2＝（27.E）16。

3（10000111）8421BCD＝（）2＝（）8＝（）10＝（）16。

[山东大学2014研]【答案】1010111；127；87；57查看答案【解析】8421BCD码就是利用四个位元来储存一个十进制的数码。

所以可先将8421BCD码转换成10进制再进行二进制，八进制和十六进制的转换。

（1000 0111）8421BCD＝（87）10＝（1010111）22进制转8进制，三位为一组，整数向前补0，因此（001 010 111）2＝（127）8。

同理，2进制转16进制每4位为一组，（0101 0111）2＝（57）16。

数制与编码1.数制和编码的基本概念▪数制数制是用一组固定的数字和一套统一的规则来表示数的方法。

常用的进位计数制有二进制(B)、八进制(O)、十进制(D)、十六进制(H)。

▪进位计数制有两个基本要素：基数和权（1）基数：数制所使用数码的个数。

例如，二进制的基数为2，十进制的基数为10。

（2）权：以基数为底，以某一数字所在位置的序号为指数的幂，称为该数字在该位置的权。

▪编码编码是采用少量的基本符号，选用一定的组合原则，以表示大量复杂多样的信息的技术。

任何信息必须转换成二进制形式数据才能由计算机进行处理、存储和传输。

2. 不同进位数制的特点▪十进制（Decimal）十进制的特点是：用10个数码（0~9）表示所有的数,基数是10, 采用逢十进一的计数方法。

▪二进制（Binary）二进制的特点是：由0、1组成，基数是2，加法采用“逢二进一”、减法采用“借一当二”的运算规则。

▪十六进制（Hexadecimal）十六进制：由0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F组成，基数是16，加法用“逢十六进一”、减法采用“借一当十六”的运算规则。

▪八进制（Octal）八进制数的特点是：由0，1，2，3，4，5，6，7组成，基数是8，加法采用“逢八进一”、减法用“借一当八”的运算规则。

3. 进制数的转换(1)二进制<-->八进制数转换(2)十进制转为八进制(3)十六进制转为八进制4. 常见的信息编码▪BCD码二进制编码的十进制数，简称BCD码(Binarycoded Decimal)。

这种方法是用4位二进制码的组合代表十进制数的0，1，2，3，4，5，6 ，7，8，9 十个数符。

▪ASCII码ASCII（American Standard Code for Information Interchange，美国信息交换标准代码），它是现今最通用的单字节编码系统，并等同于国际标准ISO/IEC 646。

计算机基础知识之数制与编码数制是计算机基础知识中非常重要的一部分，它涉及到了计算机中数字的表示和存储方式。

编码则是将数字和字符等信息转换成计算机能够识别和处理的形式。

在计算机领域中，常用的数制有二进制、十进制、十六进制等，而编码方式常见的有ASCII、Unicode、UTF-8等。

接下来，我们将详细介绍数制与编码的概念、特性以及在计算机中的运用。

一、数制1.二进制二进制是计算机中最基本的数制。

它使用了 0 和 1 两个数字，表示任何一个二进制位(bit)的状态。

二进制的每一位表示2的幂，从右到左依次是1、2、4、8、16、32...二进制数的转换和计算相对复杂，因此在计算机中常用于存储和处理数据。

2.十进制十进制是人类最常用的数制。

它使用了0-9十个数字，每一位表示10的幂。

十进制数的转换和计算相对简单，因此在日常生活和大多数计算中都使用十进制。

3.十六进制十六进制是二进制的一种表示方式，它使用了0-9和A-F十六个数字，每一位表示16的幂。

十六进制数比较紧凑且易于理解，因此在计算机领域中经常用于表示二进制值，尤其是内存地址和寄存器的值。

4.八进制八进制使用了0-7八个数字，每一位表示8的幂。

八进制在计算机领域中应用较少，通常仅用于一些特定的场景。

5.其他进制除了二进制、十进制、十六进制和八进制外，还有其他一些进制，如二十四进制、三十六进制等。

但它们在计算机领域中使用相对较少。

二、编码编码是将数字、字符和其他信息转换成计算机能够理解和处理的形式。

常见的编码方式有ASCII、Unicode、UTF-8等。

1.ASCII码ASCII (American Standard Code for Information Interchange)是计算机中最早使用的编码方式，它共定义了128个字符，包括数字、字母、符号和控制字符等。

每个字符用一个字节(8位）来表示，其中的 7位用于字符的编码，最高位用于保持数据的完整性。

第1次课数字信号数制、码制●本次重点内容：1、数字信号2、数制转换3、BCD码●教学过程1.1数字电路概述电信号按工作特点来划分，有模拟信号和数字信号两类。

模拟信号的特点是在时间上和幅度上都是连续变化的；数字信号的特点是在时间和幅度上都是离散的。

1.1.1脉冲信号脉冲信号是指在很短时间内出现的电压或电流信号。

广义上讲，凡是不连续非正弦信号都泛称为脉冲信号。

它具有不连续性和突变性。

脉冲信号是数字信号的基本形式。

常见的脉冲信号波形有：(a)尖脉冲、(b)矩形波、(c)方波、(d)锯齿波、(e)阶梯波、(f)钟形波。

分别如图1-1所示：(a) 尖脉冲 (b) 矩形波(c) 方波 (d) 锯齿波(e) 阶梯波 (f)钟形波图1-1脉冲波形1.1.2 脉冲的参数：1、脉冲幅度U m ：又称脉冲振幅，又叫脉冲峰值，用来表示脉冲信号的强弱。

它指是脉冲电压波形变化的最大值U m。

单位为伏特，符号为V。

2、脉冲上升时间t r ：又叫脉冲上升沿或脉冲前沿，是指脉冲波形0.1U m 上升到0.9U m 所需要的时间。

单位为秒，符号为s。

3、脉冲下降时间t f :脉冲波形从0.9U m下降到0.1U m所需要的时间。

单位为秒，符号为s。

4、脉冲宽度t w ：从脉冲波形上升沿0.5U m到下降沿0.5U m所需的时间。

单位为秒，符号为s。

5、脉冲周期T ：在周期性脉冲中，相临两个脉冲波形重复出现所需的时间。

单位为秒，符号为s。

6、脉冲频率f：每秒时间内脉冲出现的次数f＝1 / T。

单位为赫兹，符号为Hz。

7、占空比q ：脉冲宽度t w 与脉冲重复周期T 的比值q = t w / T。

如方波的占空比q为1/2。

q是描述脉冲波形疏密的参数，它没有单位。

实际矩形脉冲波形的几个重要参数如图1-2所示：0.10.9U0.5U图1-2 脉冲波形的主要参数1.2 数制和码制1.2.1 数制一、十进制：十进制数的特点是数字的每一位都由0～9中的一个数码组成，用于数制中表示数量特征的数称为基数。

数制和码制数字电路是数字IC设计的基础，而数制和码制往往又是数字电路的基础，因此数制和码制是数字IC设计基础的基础。

在这里，我将记录关于数制与码制的一些主要知识点，有些知识点我是学了数电半年或者一年之后才发现，原来数电还有这样子的东西，于是整理在这里，仅供参考，有误请评论指出。

一、数制这里不进行记录什么二进制、十进制之类的基本概念，只介绍一些主要的知识点。

1、数制之间的转换（1）关于二进制的一些概念这里主要记录一下位、比特对于二进制的描述，是比较基础的东西。

位宽/比特：一个二进制数，有它的位宽，有多少个0/1，它位宽就是多少；比如二进制数10110，它的位宽就是5，从第0位到第4位；也说这是一个5位宽的二进制数，或者说这个二进制数宽度大小是5比特，数值大小为22（默认数值大小一般说的是十进制的数值大小）。

最高位和最低位：对于上面的10110，最高位是1，最低位是0；最高位是第4位，最低位是0（2）二进制转换成十进制：①二进制转换成十进制方法为：把二进制数按权展开、相加即得十进制数。

②举例：二进制数10011.01,位数为1的有第4位，第1位，第0位，第-2位，那么就有：10011的十进制数值（注意说到数值，默认是转换为十进制时数的大小）为：2^4 + 2^1 + 2^0 + 2^(-2) = 19.25十进制转换成二进制：①转换方法就是：整数部分，除二取余；小数部分，乘二取整(小数部分一般会说明要精确到小数点多少位)。

②举例说明:将35.63转换成二进制数，小数部分精确到小数点后3位那么对于整数部分，除二取余：整数部分的二进制数就是100011。

对于小数部分：乘二取整0.63*2 = 1.26,取1;0.26*2 = 0.52，取0；0.52*2 = 1.04，取1；已经达到三位了。

因此小数部分就是101因此35.63的二进制表示为100011.101。

（3）二进制转换成八进制：①方法：从小数点向两边展开，每三位二进制划分为一组，每一组的的十进制就是对应的八进制，（注意，最高位或者最低位不够3位要补0）。