PLC中数制和码制的关系

plc中常用码制PLC中常用码制PLC是现代工业控制系统中的核心设备之一，其主要功能是对工业生产过程进行自动化控制。

在PLC的工作过程中，码制是一个十分重要的概念。

本文将介绍PLC中常用的码制，以及它们在自动化控制中的应用。

1. 二进制码二进制码是PLC中最基本、最常用的码制之一。

它由0和1两个数字组成，表示开/关状态。

在PLC中，所有输入和输出都是以二进制码形式表示。

例如，当传感器检测到某个工业设备发生故障时，会产生一个二进制码信号，通知PLC执行相应的控制程序。

2. BCD码BCD码是二进制码的一种扩展形式，它将0~9这10个数字分别用4位二进制码表示。

BCD码在数字控制领域应用广泛，例如在工业自动化控制中，PLC可通过BCD码来控制数字显示屏的输出。

3. 格雷码格雷码是一种二进制码，它的最大特点是相邻两个码之间只有一位二进制数不同。

在PLC中，格雷码可用于减少数字转换时的误差，提高数字控制的精度。

4. ASCII码ASCII码是一种基于拉丁字母的字符编码标准。

在PLC中，ASCII 码可用于控制文本输出。

例如，在工业自动化控制中，PLC可通过ASCII码来控制LED屏幕显示文字信息。

5. Modbus协议Modbus协议是一种基于二进制码的通讯协议，主要用于工业自动化设备之间的数据通讯。

在PLC中，Modbus协议可用于实现PLC 与其他工业设备之间的数据传输，实现设备之间的联动控制。

6. CAN总线CAN总线是一种基于二进制码的实时通讯协议，主要用于汽车、机车等移动设备的控制系统中。

在PLC中，CAN总线可用于实现PLC与车辆控制器之间的数据传输，实现车辆控制系统的自动化控制。

7. 485总线485总线是一种基于二进制码的串行通讯协议，主要用于工业自动化设备之间的数据传输。

在PLC中，485总线可用于实现PLC与其他工业设备之间的数据传输，实现设备之间的联动控制。

码制在PLC的自动化控制中起着至关重要的作用。

PLC常用数制及转换方法一、什么是进位计数制数制也称计数制,是指用一组固定的符号和统一的规则来表示数值的方法。

按进位的原则进行计数的方法,称为进位计数制。

比如，在十进位计数制中,是按照“逢十进一”的原则进行计数的。

常用进位计数制：1、十进制(Decimal notation)，有10个基数：0 ~~ 9 ，逢十进一；2、二进制(Binary notation)，有2 个基数：0 ~~ 1 ，逢二进一；3、八进制(Octal notation)，有8个基数：0 ~~ 7 ，逢八进一；4、十六进制数(Hexdecimal notation)，有16个基数：0 ~~ 9，A，B，C，D，E，F (A=10,B=11,C=12,D=13,E=14,F=15) ，逢十六进一。

二、进位计数制的基数与位权'基数'和'位权'是进位计数制的两个要素。

1、基数：所谓基数，就是进位计数制的每位数上可能有的数码的个数。

例如，十进制数每位上的数码，有'0'、'1'、'3',…，'9'十个数码，所以基数为10。

2、位权：所谓位权，是指一个数值的每一位上的数字的权值的大小。

例如十进制数4567从低位到高位的位权分别为100、101、102、103。

因为：4567＝4x103＋5x 102＋6x 101 ＋7x1003、数的位权表示：任何一种数制的数都可以表示成按位权展开的多项式之和。

比如：十进制数的435．05可表示为：435．05＝4x102＋3x 101＋5x100＋0x10－1 ＋5x 10－2位权表示法的特点是：每一项＝某位上的数字X基数的若干幂次；而幂次的大小由该数字所在的位置决定。

三、二进制数计算机中为何采用二进制：二进制运算简单、电路简单可靠、逻辑性强。

1、定义：按“逢二进一”的原则进行计数，称为二进制数，即每位上计满2 时向高位进一。

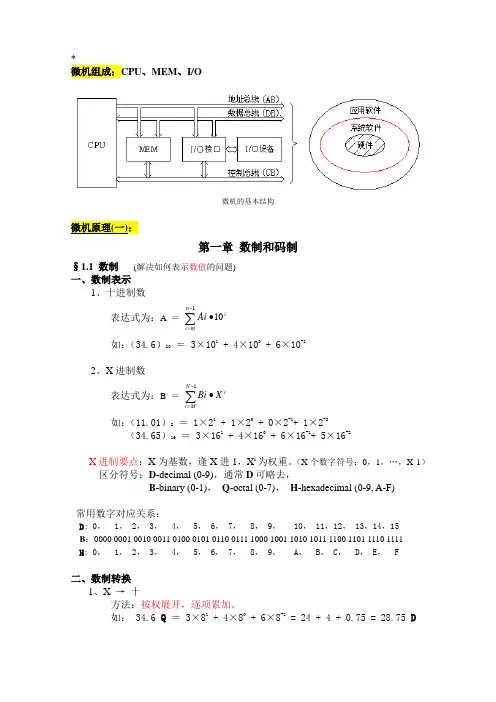
*微机组成：CPU、MEM、I/O微机的基本结构微机原理(一)：第一章数制和码制§1.1 数制(解决如何表示数值的问题)一、数制表示1、十进制数表达式为：A ＝∑-=•110 nmi iAi如：（34.6）10＝ 3×101 + 4×100 + 6×10-1 2、X进制数表达式为：B ＝∑-=•1 NM iiX Bi如：（11.01）2＝ 1×21 + 1×20 + 0×2-1+ 1×2-2（34.65）16＝ 3×161 + 4×160 + 6×16-1+ 5×16-2X进制要点：X为基数，逢X进1，X i为权重。

（X个数字符号：0，1，…，X-1）区分符号：D-decimal (0-9)，通常D可略去，B-binary (0-1)，Q-octal (0-7)，H-hexadecimal (0-9, A-F)常用数字对应关系：D: 0， 1， 2， 3， 4， 5， 6， 7， 8， 9， 10， 11，12， 13，14，15B：0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111H: 0， 1， 2， 3， 4， 5， 6， 7， 8， 9， A， B， C， D， E， F二、数制转换1、X →十方法：按权展开，逐项累加。

如： 34.6 Q＝ 3×81 + 4×80 + 6×8-1 = 24 + 4 + 0.75 = 28.75 D2、十→X即：A十进制＝B X进制令整数相等，即得：A整数＝（B N-1·X N-1 + … + B1·X1）+ B0·X0此式一次除以X可得余数B0，再次除以X可得B1，…，如此直至得到B N-1令小数相等，即得：A小数＝B-1·X-1 +（B-2·X-2 + … + B-M·X-M）此式一次乘X可得整数B-1，再次乘X可得B-2，…，如此直至得到B-M.归纳即得转换方法：除X取余，乘X取整。

PLC中数值制式转换的原理及编程在PLC编程中，对于一个整数，它的二进制或16进制或10进制的数值形式会自动转换，不需人为干预。

可是将一个整数转换为BCD码或转换为AICII码，就不能自动转换，有的PLC有这样的转换指令，如S7-200，我们需要时，直接调用对应的转换指令就可以了。

可是有的PLC没有这方面的转换指令，如需要这种数值制式转换，就得自己编写转换程序。

要想编出转换程序，应必须先了解要转换的这二种数值制式之间的数学关系，只有了解了才能编出合理的转换程序。

下面我们分别介绍几种数制转换的依据及编程。

一、16进制数转换为BCD码的数学依据及编程：BCD码是以4位二进制数表示一位十进制数的一种数制形式，它源于电子线路的计数器，该计数器是由4位二进制计数器组成，4位二进制计数器共有16种输出状态：0000、0001、0010、0011……1111，由高位向低位各位权依次代表为8、4、2、1，这4位数之和表示一位16进制数或一位10进制数。

用这16种状态表示一个数的称之为二进制（或称16进制）计数器，只用这16种状态的前10种状态表示一个数的计数器，称之为10进制计数器，这十进制编码为0000、0001、0010……1000、1001，这种每4位二进制数代表一位10进制数的编码称之为8421码，即BCD码。

个位上的4位有效数（1）分别代表10进制数的8、4、2、1，十位上的4位有效数（1）分别代表10进制数的80、40、20、10，百位上的4位有效数（1）分别代表10进制数的800、400、200、100，千位上的4位有效数（1）分别代表10进制数的8000、4000、2000、1000……一个字存储器有16个位，可记录4位BCD码，一个字记录最大的BCD码为9999。

即：1001_1001_1001_1001。

了解了这些就可以进行将整数转换为BCD码，或将BCD码转换为整数的编程：（一）整数转换为BCD码编程在PLC里，整数通常是以16进制（即2进制）数的形式存放在存储器内，将整数转换为BCD码编程思路是这样：将原整数存放在M1存储器里，M2为BCD码存放区，先将M2清0，如最大整数<10000，则M2选用一个字存储器就够，计算过程是：先判断M1是否大于10进数8000（转换16进制数为1F40），如大于，用M1值- 1F40，将差－－>M1，M2加1 ，如小于，不作减8000运算，接着将M2左移一位，再判断M1是否大于10进数4000（转算16进制数为0FA0），如大于，用M1值- FA0，将差－－>M1，M2加 1 如小于，不作减运算，接着将M2 左移一位.....接着按同样判断处理过程，判断2000、1000、800、400、200、100、80、40、20、10，判断完10后，将M2左移4位，再将M1或到M2中，此时的M2即为转换BCD码数。

数制与码制1.数制数制即计数体制，是人们进行计数方法和规则的。

数字电路中采用的是二进制，是因为二进制只有“1”和“0”两个数码，可以方便用电流的有无、电压高低、电路通断等两种状态表示。

2.不同数制间的转换2.1 其他进制转化为十进制方法是：转换时，将其他进制按权位展开，然后各项再相加，就可得到相应的十进制数。

例：N=（1011.01)B=( ? )D按权展开：N=1*2^3+0*2^2+1*2^1+1*2^0+0*2*-1+1*2^-2=8+2+1+0.25=(11.25)D B代表二进制，D代表十进制；权：小数点之前从零开始不断增加，小数点之后从-1开始不断减小2.2十进制转化为其他进制方法是：转化时，分整数部分和小数部分，整数部分除基取余逆序，小数部分乘基取整正序。

例：十进制转化为二进制302.8125整数部分： 302/2=151 余0151/2=75 余175/2=37 余137/2=18 余118/2=9 余09/2=4 余14/2=2 余02/2=1 余01/2=0 余1故整数部分转化为二进制为（302）D=（100101110）B小数部分：0.1825*2=1.625 取整10.625*2=1.25 取整10.25*2=0.5 取整00.5*2=1.0 取整1故小数部分转化为二进制为（0.1825）D=（1101）B故（302.8125）D=(100101110.1101)B2.3二进制与八进制、十六进制的相互转化二进制转化为八进制和十六进制时，将要转化的二进制从低位到高位每3位或4位一组，高位不足时在有效位前添“0”，然后把每组二进制数转化为相应的八进制数或十六进制数。

例：（0101/1110.1011/0010）B=(5E.B2)H(8FA.C6)H=(1000/1111/1010.1100/0110)B3.码制码制即编码体制，在数字电路中主要是指用二进制数来表示非二进制数字以及字符的编码方法和规则。

数制和码制计算机内部的所有的电器元件的工作状态都是0、1两种状态，计算机的基础是“二进制”。

数字电路的信号只有高、低电平两个取值。

电子器件的工作状态只有导通（开）、截止（关）。

一、基本概念定义:用一组固定的数字和一套统一的规则来表示数值的方法。

（1）数码：一组用来表示某种数制中基本数值大小的不同数字符号。

以十进制为例，十进制有0、1、2、3、4、5、6、7、8、9十个数码。

（2）基数：某数制可以使用的基本数码的个数。

例如，二进制的基数为2，八进制的基数为8，十进制的基数为10。

（3）位权：权是基数的幂，表示数制中某一位上的1在不同位置上所表示的数值大小。

例如十进制数321，3的位权是100，2的位权是10，3的位权是1。

（4）数制：计数的规则。

按进位的原则进行计数，称为进位计数制，简称数制。

例如，十进制逢十进一，二进制逢二进一。

二、十进制（D）数字符号（系数）：0、1、2、3、4、5、6、7、8、9计数规则：逢十进一基数：10权：10的幂三、二进制（B）数字符号：0、1例：（547）10=5×102+4×101+7×100计数规则：逢二进一基数：2权：2的幂四、八进制（O）数字符号：0—7计数规则：逢八进一基数：8权：8的幂五、十六进制（H）数字符号：0—9、A、B、C、D、E、F计数规则：逢十六进一基数：16权：16的幂例：（1011101）2=（1×26+0×25+1×24+1×23+1×22+0×21+1×20）10=（64+0+16+8+4+0+1）10=（93）10六、数制间的转换1.各种数制转换成十进制按权展开求和2.十进制转换为二进制整数和小数分别转换整数部分：除2取余法小数部分：乘2取整法3.二进制与十六进制间的相互转换从小数点开始，整数部分向左(小数部分向右)四位一组，最后不足四位的加0补足四位，再按顺序写出各组对应的十六进制数。

∙前言∙因为电路状态只有“开”和“关”两种状态，为了在电路中进行数字计算，所以在计算机（电路）中使用了二进制计数系统，该系统只使用0和1。

∙在存储器中，也是使用二进制的计数系统。

∙二进制是以2为基的数制。

在二进制系统中，用于表示高和低的两个逻辑电平分别是逻辑1和逻辑0。

∙在数字电路中，电平表示位（bit）。

∙由于二进制用于所有的数学系统，所以就需要有一种方式将我们常用的十进制转化为二进制。

另外，为了将数字电路输出的二进制转化为人们可使用的十进制形式，还需要一种将二进制转化为十进制的方法。

∙前言∙本章节就简单讲述以下内容：– PLC中常用的数制；–数制之间的相互转化方式；–各种数制在PLC中的存储方式。

∙数制∙在PLC中，常用的数制有以下几种：–十进制–二进制–八进制–十六进制– BCD码– BIN码–格雷码（不做讲解）– 7段码（不做讲解）∙下面分别讲述这几种编码的表述形式与转化方式∙十进制回顾一∙十进制是一个位权计数系统；所谓位权计数系统，意思就是每一个数字所在的位置都有一个特定的权（值）。

∙例如：数字5根据小数点的不同位置代表不同的值。

数字0.5，5，500都包含一个5，但是每个5的位置不同，所以这几个数大小就不一样。

∙在十进制中，使用0，1，2，3，4，5，6，7，8，9十个基本符号，每个符号称为一个数位。

∙例如：60328.4的计算方法：6x104+ 0x103 + 3x102 + 2x101 + 8x100 + 4x10-1∙十进制计数系统回顾二∙在本例中将每个位置的权值相加，用来确定十进制的值。

∙6x104+ 0x103 + 3x102 + 2x101 + 8x100. + 4x10-1=60328.4∙需要注意的是，本例中0没有值，但是对于位权而言，还需要0作为一个占位符。

∙在上面的讲述中，由于大家都已经习惯于使用十进制思考，所以这样处理就显得毫无必要，但是对于下面要讲到的数制来说，该处理过程就非常有必要了。

一、数制和码制数制即十进制、二进制、十六进制、八进制。

码制即ASCII码、BCD码等等，这些只要稍作了解即可，不必深究。

十进制：从小大到学的，我也不知道什么定义，反正就是0123456879，逢十进一嘛。

二进制：数字电路中的基本工作信号是二进制的数字信号，即0和1这两个基本数字。

8和16进制不必深究了，除非你搞网络通讯要用它来编校验码（网上一般能找到这样的校验程序）。

所以，在这里，要详究的就是十进制与二进制之间的转换了。

这个非常重要，搞不清2进制，你就不知道“定时器为什么最大值是32767”等诸如此类的问题。

二、数据类型以西门子S7-200系列说例（不同的编程软件，数据类型的长度有细微变化）数据类型分为：位（Bit）、字节（Byte）、字（Word）、双字（Double Word）、整数（Int）、双整（Double Word）、实数（Float 即浮点数，带小数点的，一定要以小数形式表示，如2.1、1.0）。

我们要知道8位=1字节，2字节=1字（整数），2字（整数）=1双字（双整）=1实数，这三个公式表示各数据间的长度比，某种意义上实数和双字、双整可相等，因为双字和双整不能表示小数，所以某种意义上又不等，但数据长度都是32位。

还有字符串等其它数据类型，因初学者不常用，故不作过多介绍，等你有一定PLC基础后再作了解会更省时间，事半功倍。

三、逻辑代数逻辑代数又称布尔代数，是研究逻辑电路的数学工具，它为分析和设计逻辑电路提供了理论基础。

逻辑代数所研究的内容，是逻辑函数与逻辑变量之间的关系。

逻辑变量和我们中学时代学的数学中的代数一样，可以用A、B、C等字母表示。

逻辑代数就是用以描述逻辑关系，反映逻辑变量运算规律的数学。

打个比方：1 1=2是我们中学时代学的普通代数a b=c是我们现在所要讲的逻辑代数，至于a、b、c具体是什么值不一定。

逻辑代数运算普通代数运算有加减乘除，在逻辑代数中，一样有它自己的运算方式。

第1章数制与码制1.1 概述电子信号可用于表示任何信息，如符号、文字、语音、图像等，从表现形式上可归为两类：模拟信号和数字信号。

模拟信号的特点是时间和幅度上都连续变化（连续的含义是在某一取值范围内可以取无限多个数值）。

交流放大电路的电信号就是模拟信号，如图1-1所示。

我们把工作在模拟信号下的电子电路称为模拟电路。

数字信号是时间和幅度上都不连续变化的离散的脉冲信号，例如图1-2所示。

用数字信号对数字量进行算术运算和逻辑运算的电路称为数字电路，或数字系统。

由于它具有逻辑运算和逻辑处理功能，所以又称为数字逻辑电路。

图1-1 图1-2数字电路通常是根据脉冲信号的有无来进行工作的，而与脉冲幅度无关，所以抗干扰能力强、准确度高。

虽然数字信号的处理电路比较复杂，但因信号本身的波形十分简单，只有两种状态—有或无，在电路中具体表现为高电位和低电位（通常用1和0表示），所以用于数字电路的半导体管不是工作在放大状态而是工作在开关状态，要么饱和导通，要么截止，因此制作时工艺要求相对低，易于集成化。

随着数字集成电路制作技术的发展，数字电路在通信、计算机、自动控制、航天等各个领域获得了广泛的应用。

数字信号通常都是用数码表示的。

数码不仅可以用来表示数量的大小，还可以用来表示事物或事物的不同状态。

用数码表示数量大小时，需要用多位数码表示。

通常把多位数码中每一位的构成方法及从低位到高位的进位规则称为数制。

在用于表示不同事物时，这些数码已经不再具有表示数量大小的含义，它们只是不同事物的代号。

比如，我们每个人的身份证号码，这些号码仅仅表示不同对象，没有数量大小的含义。

为了便于记忆和查找，在编制代码时总要遵循一定的规则，这些规则就称为码制。

考虑到信息交换的需要，通常会制定一些大家共同使用的通用代码。

例如：目前国际上通用的美国信息交换标准代码（ASCII码，见本章第1.5节）就属于这一种。

数字电子技术1.2 几种常用的数制任何一个数都可以用不同的进位体制来表示，但不同进位计数体制的运算方法和难易程度各不相同，这对数字系统的性能有很大影响。