通信原理第5章1-2(电子工业出版社张祖凡)[23页]
- 格式:ppt
- 大小:1.33 MB
- 文档页数:55



《通信原理》习题参考答案第一章1-1. 设英文字母E 出现的概率为0.105,x 出现的概率为0.002。
试求E 及x 的信息量。
解: )(25.3105.01)(log 2bit E I ==)(97.8002.01)(log 2bit X I == 题解:这里用的是信息量的定义公式)(1log x P I a =注:1、a 的取值:a =2时,信息量的单位为bita =e 时,信息量的单位为nita =10时,信息量的单位为哈特莱2、在一般的情况下,信息量都用bit 为单位,所以a =21-2. 某信息源的符号集由A ,B ,C ,D 和E 组成,设每一符号独立出现,其出现概率分别为1/4,1/8,1/8,3/16和5/16。
试求该信息源符号的平均信息量。
解:方法一:直接代入信源熵公式:)()()()()(E H D H C H B H A H H ++++=516165316163881881441log log log log log 22222++++=524.0453.083835.0++++= 符号)/(227.2bit =方法二:先求总的信息量I)()()()()(E I D I C I B I A I I ++++= 516316884log log log log log 22222++++= 678.1415.2332++++= )(093.12bit =所以平均信息量为:I/5=12.093/5=2.419 bit/符号题解:1、方法一中直接采用信源熵的形式求出,这种方法属于数理统计的方法求得平均值,得出结果的精度比较高,建议采用这种方法去计算2、方法二种采用先求总的信息量,在取平均值的方法求得,属于算术平均法求平均值,得出结果比较粗糙,精度不高,所以尽量不采取这种方法计算注:做题时请注意区分平均信息量和信息量的单位:平均信息量单位是bit/符号,表示平均每个符号所含的信息量,而信息量的单位是bit ,表示整个信息所含的信息量。

doc文档可能在W AP端浏览体验不佳。
建议您优先选择TXT,或下载源文件到本机查看。
Part (5) 1.基本概念基本概念把信号转换成适合在信道中传输的形式的一种过程。
调制-把信号转换成适合在信道中传输的形式的一种过程。
分为基带调制和带通调制(也称载波调制)广义调制-分为基带调制和带通调制(也称载波调制)。
仅指带通调制。
在无线通信和其他大多数场合,狭义调制-仅指带通调制。
在无线通信和其他大多数场合,调制一词均指载波调制。
制一词均指载波调制。
指来自信源的基带信号。
调制信号-指来自信源的基带信号。
用调制信号去控制载波的参数的过程。
载波调制-用调制信号去控制载波的参数的过程。
未受调制的周期性振荡信号,它可以是正弦波,载波-未受调制的周期性振荡信号,它可以是正弦波,也可以是非正弦波。
是非正弦波。
载波受调制后称为已调信号。
已调信号-载波受调制后称为已调信号。
解调(检波)调制的逆过程,解调(检波)-调制的逆过程,其作用是将已调信号中的调制信号恢复出来。
号恢复出来。
解调器输入信噪比定义解调器输入信噪比定义Si Ni = 解调器输入信号的平均功率解调器输入噪声的平均功率解调器输出信噪比定义2 So 解调器输出有用信号的平均功率mo (t ) = = 2 No 解调器输出噪声的平均功率no (t )输出信噪比反映了解调器的抗噪声性能。
输出信噪比反映了解调器的抗噪声性能。
解调器的抗噪声性能制度增益定义G= S0 / N 0 Si / N i门限效应输出信噪比不是按比例地随着输入信噪比下降,而是急剧恶化的现输出信噪比不是按比例地随着输入信噪比下降,象称为门限效应。
同步解调器不存在门限效应。
象称为门限效应。
同步解调器不存在门限效应。
2. 调制的目的提高无线通信时的天线辐射效率。
提高无线通信时的天线辐射效率。
无线通信时的天线辐射效率把多个基带信号分别搬移到不同的载频处,把多个基带信号分别搬移到不同的载频处,以实现信道的多路复用,提高信道利用率。


云南民族大学教案课程名称: 通信原理授课班级: 通信工程、电子信息工程任课教师: 王霞职称: 讲师课程性质: 专业必修课授课学期: 大学三年级下学期云南民族大学教案(二)通过习题课及平时作业,掌握必要的分析方法和工程计算能力。
(三)通过实验课提高实验水平,培养工程测试的能力。
五、课程教学要求的层次课程教学要求分为了解、理解、掌握三个层次。
绪论1.1通信的基本概念通信的目的:传递消息中所包含的信息。
消息:是物质或精神状态的一种反映,例如语音、文字、音乐、数据、图片或活动图像等。
信息:是消息中包含的有效内容。
实现通信的方式和手段:非电的:如旌旗、消息树、烽火台…电的:如电报、电话、广播、电视、遥控、遥测、因特网和计算机通信等。
电信发明史:1837年:莫尔斯发明有线电报1876年:贝尔发明有线电话1918年:调幅无线电广播、超外差接收机问世1936年:商业电视广播开播……………后面讲述中,“通信”这一术语是指“电通信”,包括光通信,因为光也是一种电磁波。
在电通信系统中,消息的传递是通过电信号来实现的。
1.2通信系统的组成1.2.1 通信系统的一般模型信息源(简称信源):把各种消息转换成原始电信号,如麦克风。
信源可分为模拟信源和数字信源。
发送设备:产生适合于在信道中传输的信号。
信道:将来自发送设备的信号传送到接收端的物理媒质。
分为有线信道和无线信道云南民族大学教案八、选用教材和主要参考书:教材:《通信原理》(第六版),樊昌信、曹丽娜主编,北京:国防工业出版社,2011年8月第6版。
主要参考书:1、通信原理(第3版) 周炯盘、庞沁华、续大我北京邮电大学出版社 (2008-08)2、清华大学电子与信息技术系列教材:现代通信原理曹志刚、钱亚生清华大学出版社 (2012-11)九、教学主要内容及教学安排:第一章绪论1.4 信息及其度量信息:是消息中包含的有效内容如何度量离散消息中所含的信息量?1、度量信息量的原则:能度量任何消息,并与消息的种类无关。


第五章〔正弦载波数字调制系统〕习题及其答案【题5-1】设发送数字信息为,试分别画出 2ASK 、2FSK 、2PSK 及2DPSK 信号的波形示意图。
【答案5-1】2ASK 、2FSK 、2PSK 及2DPSK 信号的波形如下列图所示。
【题5-2】确定某2ASK 系统的码元传输速率为103Band ,所用的载波信号为()6cos 410A π⨯。
1〕设所传送的数字信息为011001,试画出相应的2ASK 信号波形示意图; 2〕求2ASK 信号的带宽。
【答案5-2】1〕由题中的确定条件可知310B R Baud =因此一个码元周期为3110s B T s R -==载波频率为664102102s f Hz ππ⨯==⨯载波周期为61102T s -=⨯所以一个码元周期内有2000个载波周期。
如下列图所示我们画出2ASK 信号的波形图,为简便,我们用两个载波周期代替2000个载波周期。
2〕依据2ASK 的频谱特点,可知其带宽为 222000B B R Hz T ===【题5-3】设某2FSK 调制系统的码元传输速率为1000Baud ,已调信号的载频为1000Hz 或 2000 HZ 。
1〕假设发送数字信息为011010,试画出相应的ZFSK 信号波形;2〕摸索讨这时的2FSK 信号应选择怎样的解调器解调?3〕假设发送数字信息是等可能的,试画出它的功率谱密度草图。
【答案5-3】1〕由题意可画出ZFSK 信号波形如下列图所示。
2〕由于ZFSK 信号载波频差较小,频谱有较大重叠,接受非相干解调时上下两个支路有较大串扰,使解调性能降低。
由于两个载频人与人构成正交信号,接受相干解调可减小相互串扰,所以应接受相干解调。
3〕该2FSK 信号功率谱密度草图如下列图所示。
【题5-4】假设在某2DPSK 系统中,载波频率为 2400 Hz ,码元速率为 1200 Band ,确定相对码序列为11000101ll 。
1〕试画出2DPSK 信号波形〔注:相对偏移ϕ∆,可自行假设〕;2〕假设接受差分相干解调法接收该信号时,试画出解调系统的各点波形;3〕假设发送信息符号0和1的概率分别为0.6和0.4,试求2DPSK 信号的功率谱密度。

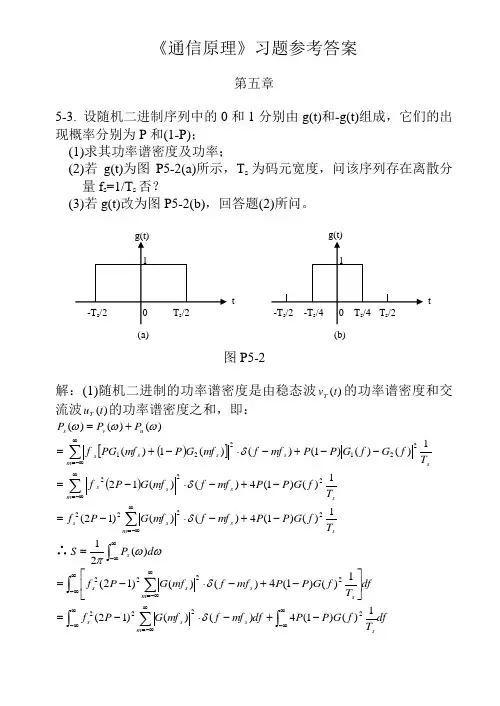
《通信原理》习题参考答案第五章5-3. 设随机二进制序列中的0和1分别由g(t)和-g(t)组成,它们的出现概率分别为P 和(1-P);(1)求其功率谱密度及功率;(2)若g(t)为图P5-2(a)所示,T s 为码元宽度,问该序列存在离散分量f s =1/T s 否?(3)若g(t)改为图P5-2(b),回答题(2)所问。
解:(1)随机二进制的功率谱密度是由稳态波)(t v T 的功率谱密度和交流波)(t u T 的功率谱密度之和,即: )()()(ωωωu v s P P P +=()[]sm s s s s T f G f G P P mf f mf G P mf PG f 1)()()1()()(1)(221221--+-⋅-+=∑∞-∞=δ ()sm s s s T f G P P mf fmf G P f1)()1(4)()(12222-+-⋅-=∑∞-∞=δ s m s s s T f G P P mf f mf G P f 1)()1(4)()()12(2222-+-⋅-=∑∞-∞=δ∴⎰∞∞-=ωωπd P S s )(21df T f G P P mf f mf G P f s m s s s ⎰∑∞∞-∞-∞=⎥⎦⎤⎢⎣⎡-+-⋅-=1)()1(4)()()12(2222δ df T f G P P df mf f mf G P f s m s s s ⎰⎰∑∞∞-∞∞-∞-∞=-+-⋅-=1)()1(4)()()12(2222δtt(a) (b) 图P5-2df f G P P T df mf f mf G P f s s m s s⎰⎰∑∞∞-∞∞-∞-∞=-+--=2222)()1(41)()()12(δ (2) 若g(t)为图P5-2(a),则g(t)经过傅立叶变化可得到它的频谱,即:)2()(ss T Sa T G ωω=将ω换为f 得: ffT f T f T T f T Sa T f G s s s ss s πππππsin sin )()(=== 判断频域中是否存在s T f 1=,就是将sT f 1=代入)(f G 中,得:0sin sin )(===ππππss T f f T f G说明sT f 1=时g(t)的功率为0,所以不存在该分量。
