(完整版)数字通信原理第五章纠错编码习题解答

信息论与编码第五章答案本页仅作为文档封面，使用时可以删除This document is for reference only-rar21year.March设信源1234567()0.20.190.180.170.150.10.01X a a a a a a a p X ⎡⎤⎧⎫=⎨⎬⎢⎥⎣⎦⎩⎭(1) 求信源熵H(X)； (2) 编二进制香农码；(3) 计算平均码长和编码效率. 解： (1)721222222()()log ()0.2log 0.20.19log 0.190.18log 0.180.17log 0.170.15log 0.150.1log 0.10.01log 0.012.609/i i i H X p a p a bit symbol==-=-⨯-⨯-⨯-⨯-⨯-⨯-⨯=∑71()0.230.1930.1830.1730.1530.140.0173.141()()/ 2.609 3.14183.1%i i i K k p x H X H X K Rη===⨯+⨯+⨯+⨯+⨯+⨯+⨯====÷=∑对习题的信源编二进制费诺码，计算编码效率.对信源编二进制和三进制哈夫曼码，计算各自的平均码长和编码效率.解：x i p(x i)编码码字k i s61s50s41s30s21x10102 x21112 x300003 x410013 x500103 s11x6001104 x7101114x i p(x i)编码码字k i s31s20s11x1221 x20002 x31012 x42022 x50102 x61112x72122设信源(1) 求信源熵H(X)；(2) 编二进制香农码和二进制费诺码；(3) 计算二进制香农码和二进制费诺码的平均码长和编码效率；(4) 编三进制费诺码；(5) 计算三进制费诺码的平均码长和编码效率；解：(1)(2)x i p(x i)p a(x i)k i码字x1010x2210x33110x441110x5511110x66111110x771111110x871111111xi p(x i)编码码字k i x1001 x210102 x3101103x41011104 x510111105x6101111106x71011111107x8111111117 (3)香农编码效率：费诺编码效率：(4)x i p(x i)编码码字k i x1001 x2111x320202x41212x5202203x612213x72022204x8122214设无记忆二进制信源先把信源序列编成数字0，1，2，……，8，再替换成二进制变长码字，如下表所示.(1) 验证码字的可分离性；(2) 求对应于一个数字的信源序列的平均长度；(3) 求对应于一个码字的信源序列的平均长度；(4) 计算，并计算编码效率；(5) 若用4位信源符号合起来编成二进制哈夫曼码，求它的平均码长，序列数字二元码字10100001110010013101000013101100001411000000015110100000016111000000001711110000000080一个来编写二进制哈夫曼码，求新符号的平均码字长度和编码效率.对题的信源进行游程编码.若“0”游程长度的截至值为16，“1”游程长度的截至值为8，求编码效率.选择帧长N = 64(1) 对00000000000000000000000000000000000000遍L-D码；(2) 对000000000010遍L-D码再译码；(3) 对000000000000000000000000000000000000000000000000000000000000000 0遍L-D码；(4) 对0遍L-D码；(5) 对上述结果进行讨论.。

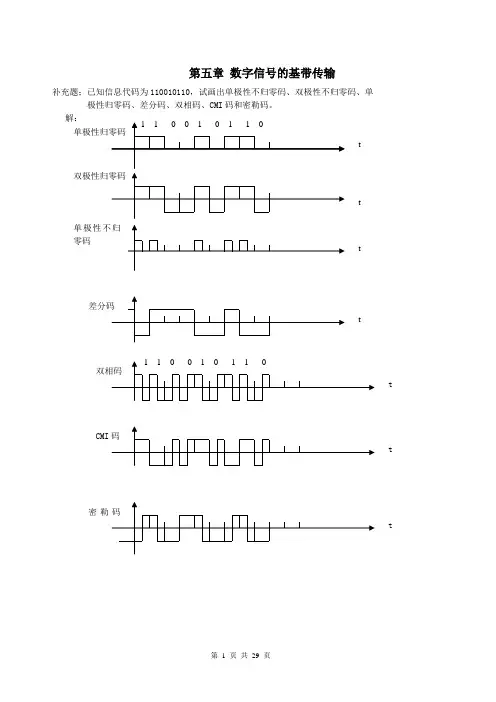
第五章习题习题5.1 若消息码序列为1101001000001，试求出AMI 和3HDB 码的相应序列。

解： AMI 码为 3HDB 码为习题5.2 试画出AMI 码接收机的原理方框图。

解：如图5-20所示。

图5-1 习题5.2图习题 5.3 设)(1t g 和)(2t g 是随机二进制序列的码元波形。

它们的出现概率分别是P 和)1(P -。

试证明：若k t g t g P =-=)](/)(1[121，式中，k 为常数，且10<<k ，则此序列中将无离散谱。

证明：若k t g t g P =-=)(/)(1121，与t 无关，且10<<k ，则有1)()]()([212=-t g t g t g P即 )()1()()()(2221t g P t g t Pg t Pg -=-=0)()1()(21=-+t g P t Pg所以稳态波为 ∑∑--+-=)()1()()(s 2s 1nT t g P nT t g P t v0)]()1()([s 2s 1=--+-=∑nT t g P nT t g P即0)(=w P v 。

所以无离散谱。

得证！习题5.4 试证明式()()()()⎰+-=1011d 2sin 2sin 4W f ft W f H Wt t h ππ。

证明：由于⎰∞∞-=df e f H t h ft j π211)()(，由欧拉公式可得⎰⎰⎰∞∞-∞∞-∞∞-+=+=fft f H ftdf f H fft ft f H t h d 2sin )(j 2cos )(d )2sin j 2)(cos ()(1111ππππ由于)(1f H 为实偶函数，因此上式第二项为0，且⎰∞∞-=f ft f H t h d )2cos()(2)(11π10100010010111000001001011+--+-++-+-+k a《通信原理》习题第五章令，'d d ,'f f W f f =+=，代入上式得⎰⎰⎰∞-∞-∞-+++=++=WWW fWt ft W f H f Wt ft W f H f t W f W f H t h d 2sin 2sin )(2d 2cos 2cos )(2'd ])'(2cos[)'(2)(1111πππππ由于)(1f H 单边为奇对称，故上式第一项为0，因此⎰⎰+=+=∞-WW fftt W f H W fftt W f H W t h 0111d 2sin )(2sin 4d 2sin )(2sin 2)(ππππ习题5.5 设一个二进制单极性基带信号序列中的“1”和“0”分别用脉冲)(t g [见图5-2的有无表示，并且它们出现的概率相等，码元持续时间等于T 。

《数字通信原理》习题解答大全第1章概述1-1 模拟信号和数字信号的特点分别是什么?答：模拟信号的特点是幅度连续；数字信号的特点幅度离散。

1-2 数字通信系统的构成模型中信源编码和信源解码的作用是什么?画出话音信号的基带传输系统模型。

答：信源编码的作用把模拟信号变换成数字信号，即完成模/数变换的任务。

信源解码的作用把数字信号还原为模拟信号，即完成数/模变换的任务。

话音信号的基带传输系统模型为1-3 数字通信的特点有哪些?答：数字通信的特点是：（1）抗干扰性强，无噪声积累； （2）便于加密处理；（3）采用时分复用实现多路通信； （4）设备便于集成化、微型化； （5）占用信道频带较宽。

1-4 为什么说数字通信的抗干扰性强，无噪声积累? 答：对于数字通信，由于数字信号的幅值为有限的离散值(通常取二个幅值)，在传输过程中受到噪声干扰，当信噪比还没有恶化到一定程度时，即在适当的距离，采用再生的方法，再生成已消除噪声干扰的原发送信号，所以说数字通信的抗干扰性强，无噪声积累。

1-5 设数字信号码元时间长度为1s μ，如采用四电平传输，求信息传输速率及符号速率。

答：符号速率为 Bd N 66101011===-码元时间 信息传输速率为 s Mbit s bit M N R /2/1024log 10log 6262=⨯=⋅==1-6 接上例，若传输过程中2秒误1个比特，求误码率。

答：76105.210221)()(-⨯=⨯⨯==N n P e传输总码元发生误码个数1-7 假设数字通信系统的频带宽度为kHz 1024，可传输s kbit /2048的比特率，试问其频带利用率为多少Hz s bit //?答：频带利用率为Hz s bit Hz s bit //2101024102048)//33=⨯⨯==（频带宽度信息传输速率η1-8数字通信技术的发展趋势是什么？答：数字通信技术目前正向着以下几个方向发展：小型化、智能化，数字处理技术的开发应用，用户数字化和高速大容量等。

第五章〔正弦载波数字调制系统〕习题及其答案【题5－1】设发送数字信息为，试分别画出 2ASK 、2FSK 、2PSK 及2DPSK 信号的波形示意图。

【答案5－1】2ASK 、2FSK 、2PSK 及2DPSK 信号的波形如下列图所示。

【题5－2】确定某2ASK 系统的码元传输速率为103Band ，所用的载波信号为()6cos 410A π⨯。

1〕设所传送的数字信息为011001，试画出相应的2ASK 信号波形示意图； 2〕求2ASK 信号的带宽。

【答案5－2】1〕由题中的确定条件可知310B R Baud =因此一个码元周期为3110s B T s R -==载波频率为664102102s f Hz ππ⨯==⨯载波周期为61102T s -=⨯所以一个码元周期内有2000个载波周期。

如下列图所示我们画出2ASK 信号的波形图，为简便，我们用两个载波周期代替2000个载波周期。

2〕依据2ASK 的频谱特点，可知其带宽为 222000B B R Hz T ===【题5－3】设某2FSK 调制系统的码元传输速率为1000Baud ，已调信号的载频为1000Hz 或 2000 HZ 。

1〕假设发送数字信息为011010，试画出相应的ZFSK 信号波形；2〕摸索讨这时的2FSK 信号应选择怎样的解调器解调？3〕假设发送数字信息是等可能的，试画出它的功率谱密度草图。

【答案5－3】1〕由题意可画出ZFSK 信号波形如下列图所示。

2〕由于ZFSK 信号载波频差较小，频谱有较大重叠，接受非相干解调时上下两个支路有较大串扰，使解调性能降低。

由于两个载频人与人构成正交信号，接受相干解调可减小相互串扰，所以应接受相干解调。

3〕该2FSK 信号功率谱密度草图如下列图所示。

【题5－4】假设在某2DPSK 系统中，载波频率为 2400 Hz ，码元速率为 1200 Band ，确定相对码序列为11000101ll 。

1〕试画出2DPSK 信号波形〔注：相对偏移ϕ∆，可自行假设〕；2〕假设接受差分相干解调法接收该信号时，试画出解调系统的各点波形；3〕假设发送信息符号0和1的概率分别为0.6和0.4，试求2DPSK 信号的功率谱密度。

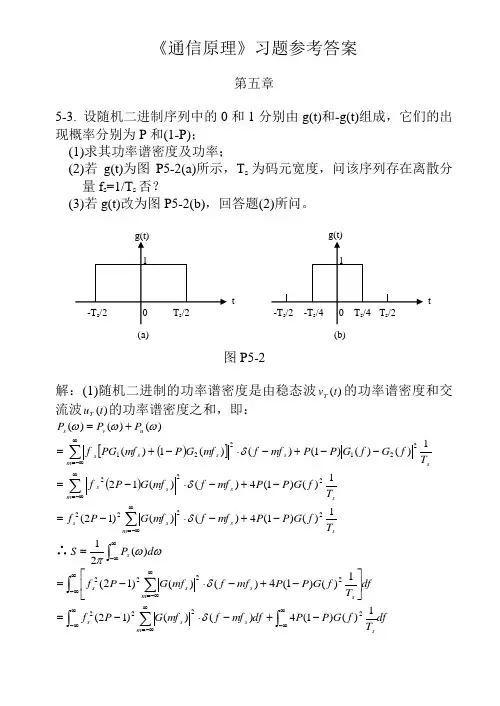
《通信原理》习题参考答案第五章5-3. 设随机二进制序列中的0和1分别由g(t)和-g(t)组成，它们的出现概率分别为P 和(1-P)；(1)求其功率谱密度及功率；(2)若g(t)为图P5-2(a)所示，T s 为码元宽度，问该序列存在离散分量f s =1/T s 否？(3)若g(t)改为图P5-2(b)，回答题(2)所问。

解：(1)随机二进制的功率谱密度是由稳态波)(t v T 的功率谱密度和交流波)(t u T 的功率谱密度之和，即： )()()(ωωωu v s P P P +=()[]sm s s s s T f G f G P P mf f mf G P mf PG f 1)()()1()()(1)(221221--+-⋅-+=∑∞-∞=δ ()sm s s s T f G P P mf fmf G P f1)()1(4)()(12222-+-⋅-=∑∞-∞=δ s m s s s T f G P P mf f mf G P f 1)()1(4)()()12(2222-+-⋅-=∑∞-∞=δ∴⎰∞∞-=ωωπd P S s )(21df T f G P P mf f mf G P f s m s s s ⎰∑∞∞-∞-∞=⎥⎦⎤⎢⎣⎡-+-⋅-=1)()1(4)()()12(2222δ df T f G P P df mf f mf G P f s m s s s ⎰⎰∑∞∞-∞∞-∞-∞=-+-⋅-=1)()1(4)()()12(2222δtt(a) (b) 图P5-2df f G P P T df mf f mf G P f s s m s s⎰⎰∑∞∞-∞∞-∞-∞=-+--=2222)()1(41)()()12(δ (2) 若g(t)为图P5-2(a)，则g(t)经过傅立叶变化可得到它的频谱，即：)2()(ss T Sa T G ωω=将ω换为f 得： ffT f T f T T f T Sa T f G s s s ss s πππππsin sin )()(=== 判断频域中是否存在s T f 1=，就是将sT f 1=代入)(f G 中，得：0sin sin )(===ππππss T f f T f G说明sT f 1=时g(t)的功率为0，所以不存在该分量。

通信原理思考题复习1.1 消息和信息有什么区别？信息和信号有什么区别？答：消息是信息的形式，信息是消息中包含的有效内容，信号是信息的载体。

1.2 什么是模拟信号，什么是数字信号？答：取值连续的信号是模拟信号，取值离散的信号是数字信号。

1.3 数字通信有何优点？答：质量好，便于差错控制和保密编码，便于存储和处理，易集成，信道利用率高信噪比高。

1.4 信息量的定义是什么？信息量的单位是什么？答：设消息x的概率为P(x),其信息量I(x)=-logap(x),.当a=2时，信息量单位为比特（bit)，当a=e时。

信息量单位为奈特（nat)，当a=10时，信息量单位为哈特莱。

1.5 按照占用频带区分，信号可以分为哪几种? 答：基带信号和带通信号。

1.6信源编码的目的是什么？信道编码的目的是什么？答：信源编码的目的是提高信号表示的有效性。

信道编码的目的是提高信号传输的可靠性。

1.7 何谓调制？调制的目的是什么？答：对信号进行调整就是调节。

调制的目的是使经过调制的信号适合信道的传输特性。

1.8 数字通信系统有哪些性能指标？答：主要有传输速率、错误率、频带利用率和能量利用率。

1.9 信道有哪些传输特性？答：噪声特性、频率特性、线性特性和时变特性等。

1.10无线信道和有线信道的种类各有哪些？答：无线信道的种类是按电磁波的频率划分的，主要分为无线电波，微波和光波。

有线信道主要有三类，即明线，对称电缆和同轴电缆，还有传输光信号的光纤。

1.11信道模型有哪几种？答：调制信道模型和编码信道模型。

1.12什么是调制信道？什么是编码信道？答：将发送端的调制器输出至接收端调制器输入端之间的部分称之为调制信道。

而将编码器输出端至解码器输入端之间的部分称之为编码信道。

1.13 何谓多径效应？答：信号经过多条路径到达接收端，而且每条路径的时延和衰减不尽相同，造成接收端的信号幅度和随机变化，这一现象称为多径效应。

1.14 电磁波有哪几种传播方式？答：电磁波有地波传播、天波传播和视线传播三种传播方式。

信息论与编码第五章习题参考答案5.1某离散⽆记忆信源的概率空间为采⽤⾹农码和费诺码对该信源进⾏⼆进制变长编码，写出编码输出码字，并且求出平均码长和编码效率。

解：计算相应的⾃信息量1)()(11=-=a lbp a I ⽐特 2)()(22=-=a lbp a I ⽐特 3)()(313=-=a lbp a I ⽐特 4)()(44=-=a lbp a I ⽐特 5)()(55=-=a lbp a I ⽐特 6)() (66=-=a lbp a I ⽐特 7)()(77=-=a lbp a I ⽐特 7)()(77=-=a lbp a I ⽐特根据⾹农码编码⽅法确定码长1)()(+<≤i i i a I l a I平均码长984375.164/6317128/17128/1664/1532/1416/138/124/112/1L 1=+=?+?+?+?+?+?+?+?=由于每个符号的码长等于⾃信息量，所以编码效率为1。

费罗马编码过程5.2某离散⽆记忆信源的概率空间为使⽤费罗码对该信源的扩展信源进⾏⼆进制变长编码，(1) 扩展信源长度，写出编码码字，计算平均码长和编码效率。

(2) 扩展信源长度，写出编码码字，计算平均码长和编码效率。

(3) 扩展信源长度，写出编码码字，计算平均码长和编码效率，并且与(1)的结果进⾏⽐较。

解：信息熵811.025.025.075.075.0)(=--=lb lb X H ⽐特/符号（1）平均码长11=L ⽐特/符号编码效率为%1.81X)（H 11==L η（2）平均码长为84375.0）3161316321631169（212=?+?+?+?=L ⽐特/符号编码效率%9684375.0811.0X)（H 22===L η（3）当N=4时，序列码长309.3725617256362563352569442569242562732562732256814=?+?+??+??+??+?+??+?=L平均码长827.04309.34==L %1.98827.0811.0X)（H 43===L η可见，随着信源扩展长度的增加，平均码长逐渐逼近熵，编码效率也逐渐提⾼。

第五章 纠错编码习题解答1、已知一纠错码的三个码组为(001010)、(101101)、(010001)。

若用于检错，能检出几位错码？若用于纠错，能纠正几位错码？若纠检错结合，则能纠正几位错码同时检出几位错码？[解]该码的最小码距为d 0=4，所以有：若用于检错，由d 0≥e +1，可得e =3，即能检出3位错码； 若用于纠错，由d 0≥2t +1，可得t =1，即能检出1位错码； 若纠检错结合，由d 0≥e +t +1 （e >t ），可得t =1，e =2，即能纠正1位错码同时能检出2位错码。

2、设某(n ,k )线性分组码的生成矩阵为：001011100101010110G ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦①试确定该(n ,k )码中的n 和k ； ②试求该码的典型监督矩阵H ； ③试写出该码的监督方程； ④试列出该码的所有码字； ⑤试列出该码的错误图样表； ⑥试确定该码的最小码距。

[解] ①由于生成矩阵G 是k 行n 列，所以k =3，n =6。

②通过初等行变换，将生成矩阵G 变换成典型生成矩阵[]100101010110001011k G I Q ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦由于101110110011011101T Q P Q ⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦，　＝＝，可知典型监督矩阵为 []110100011010101001r H PI ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦＝ ③监督方程为542431530000a a a a a a a a a ⊕⊕=⎧⎪⊕⊕=⎨⎪⊕⊕=⎩④所有码字见下表⑤错误图样表即错误图样与校正子关系表，见下表⑥线性码的最小码距为码字的最小重量（全零码除外），所以该码的最小码距为3。

3、已知一种(7,3)循环码的全部码组为：0000000 0101110 1001011 1100101 0010111 0111001 1011100 1110010试求该码的生成多项式g (x )、典型生成矩阵G 和典型监督矩阵H ；[解]由循环码的原理知，生成多项式g (x )对应的码字为前k -1位码元均为“0”的码字，即“0010111”，所以有g (x )=x 4+x 2+x +1则生成矩阵为2643253242()1011100()0101110()10010111x g x x x x x G xg x x x x x g x x x x ⎡⎤⎡⎤+++⎡⎤⎢⎥⎢⎥⎢⎥==+++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+++⎣⎦⎣⎦⎣⎦ 典型化可得典型生成矩阵[]100101101011100010111k G I Q ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦由于110101101111101110111101TQ P Q ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦，　＝＝，可得典型监督矩阵为 []1101000011010011100101010001r H PI ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦＝4、已知一个(3,1,4)卷积码编码器的输出和输入关系为：11212343134c b c b b b b c b b b ==⊕⊕⊕=⊕⊕试画出该编码器的电路方框图和码树图。

第5章 数字基带传输系统5.1 学习指导 5.1.1 要点本章的要点主要有数字基带传输系统结构及各部件功能；基带信号常用波形及其频谱特性；基带传输常用码型的编译及其特点；码间串扰和奈奎斯特第一准则；理想低通传输特性和奈奎斯特带宽；升余弦滚将特性；第一类部分响应系统；无码间串扰基带系统的抗噪声性能；眼图和均衡的概念。

1.数字基带传输系统数字基带传输系统：不经载波调制而直接传输数字基带信号的系统，其基本结构如图5-1所示。

主要有发送滤波器、信道、接收滤波器、同步提取电路以及抽样判决器组成。

发送滤波器用于产生适合于信道中传输的基带信号波形。

信道是基带信号传输媒质（通常为有线信道）。

加性n (t )是均值为零的高斯白噪声。

接收滤波器的功能接收有用信号，滤除带外噪声，对信道特性均衡，使输出的基带波形有利于抽样判决。

同步提取即从接收信号中提取用来抽样的定位脉冲。

抽样判决器用来对对接收滤波器的输出波形进行抽样、判决和再生（恢复基带信号）。

图5 - 1 数字基带传输系统的原理方框图发送滤波器信道接收滤波器抽样、判决器e (t )n (t)位同步提取y (t )2.数字基带信号及其频谱特性(1) 数字基带信号数字基带信号用不同的电平或脉冲来表示不同的消息代码。

数字基带信号的单个脉冲有矩形脉冲、余弦脉冲、升余弦脉冲、高斯脉冲等等形式。

常用的基本信号波形有：单极性与双极性波形、不归零码与归零码波形、差分波形、多电平波形等。

数字基带信号通常是一个随机的脉冲序列。

若其各码元波形相同而电平取值不同，则可表示为()()nsn s t a g t nT ∞=-∞=-∑ (5-1)式(5-1)中，a n 是第n 个码元所对应的电平值（随机量）；T s 为码元持续时间；g (t )为某种脉冲波形。

一般情况下，数字基带信号可表示为()()nn s t s t ∞=-∞=∑ (5-2)(2) 基带信号的频谱特性数字基带信号s (t )的频谱特性可以用功率谱密度来描述。

信息论与编码第五章答案5.1 设信源1234567()0.20.190.180.170.150.10.01Xa a a a a a a p X ⎡⎤⎧⎫=⎨⎬⎢⎥⎣⎦⎩⎭ (1) 求信源熵H(X)； (2) 编二进制香农码；(3) 计算平均码长和编码效率. 解： (1)721222222()()log ()0.2log 0.20.19log 0.190.18log 0.180.17log 0.170.15log 0.150.1log 0.10.01log 0.012.609/i i i H X p a p a bit symbol==-=-⨯-⨯-⨯-⨯-⨯-⨯-⨯=∑(2)(3)71()0.230.1930.1830.1730.1530.140.0173.141()()/ 2.609 3.14183.1%i i i K k p x H X H X K Rη===⨯+⨯+⨯+⨯+⨯+⨯+⨯====÷=∑5.2 对习题5.1的信源编二进制费诺码，计算编码效率.解：a i p(a i)编码码字k ia10.20002 a20.19100103 a30.1810113 a40.1710102 a50.15101103 a60.11011104 a70.011111145.3 对信源编二进制和三进制哈夫曼码，计算各自的平均码长和编码效率.解：二进制哈夫曼码：x i p(x i)编码码字k i s61s50.610s40.391s30.350s20.261x10.20102 x20.191112 x30.1800003 x40.1710013 x50.1500103 s10.111x60.1001104 x70.01101114三进制哈夫曼码：x i p(x i)编码码字k i s31s20.540s10.261x10.2221 x20.190002 x30.181012 x40.172022 x50.150102 x60.11112 x70.0121225.4 设信源(1) 求信源熵H(X)；(2) 编二进制香农码和二进制费诺码；(3) 计算二进制香农码和二进制费诺码的平均码长和编码效率；(4) 编三进制费诺码；(5) 计算三进制费诺码的平均码长和编码效率；解：(1)(2)二进制香农码：x i p(x i)p a(x i)k i码字x10.5010x20.250.5210x30.1250.753110x40.06250.87541110x50.031250.9375511110x60.0156250.968756111110x70.00781250.98437571111110x80.00781250.992187571111111二进制费诺码：xi p(x i)编码码字k i x10.5001 x20.2510102 x30.125101103 x40.06251011104x50.0312510111105 x60.015625101111106 x70.00781251011111107 x80.0078125111111117 (3)香农编码效率：费诺编码效率：(4)x i p(x i)编码码字k i x10.5001 x20.25111 x30.12520202 x40.06251212 x50.03125202203 x60.01562512213 x70.00781252022204 x80.0078125122214 (5)5.5 设无记忆二进制信源先把信源序列编成数字0，1，2，……，8，再替换成二进制变长码字，如下表所示.(1) 验证码字的可分离性；(2) 求对应于一个数字的信源序列的平均长度；(3) 求对应于一个码字的信源序列的平均长度；(4) 计算，并计算编码效率；(5) 若用4位信源符号合起来编成二进制哈夫曼码，求它的平均码长，并计算编码效率.序列数字二元码字101000011100100131010000131011000014110000000151101000000161110000000017111100000000805.6 有二元平稳马氏链，已知p(0/0) = 0.8，p(1/1) = 0.7，求它的符号熵.用三个符号合成一个来编写二进制哈夫曼码，求新符号的平均码字长度和编码效率.5.7 对题5.6的信源进行游程编码.若“0”游程长度的截至值为16，“1”游程长度的截至值为8，求编码效率. 5.8 选择帧长N= 64(1) 对001000000000000000000000000000000100000000000000 0000000000000000遍L-D码；(2) 对100001000010110000000001001000010100100000000111 0000010000000010遍L-D码再译码；(3) 对000000000000000000000000000000000000000000000000 0000000000000000遍L-D码；(4) 对101000110101110001100011101001100001111011001010 00110101011010010遍L-D码；(5) 对上述结果进行讨论.。