通信原理第五章答案

移动通信原理习题答案5章Chapter 11、为什么寻呼系统需要提供较低的数据传输速率？较低的数据速率如何实现更好的覆盖？答：寻呼系统⽤来提供⾼度可靠地覆盖，甚⾄包括建筑物内部。

⽽建筑物能削弱⽆线信号20-30dB 。

因此我们希望在信号传输过程中提⾼信噪⽐。

发射功率是⼀定的，因此提⾼信噪⽐要求降低接收端的噪声电平，因为噪声电平和射频带宽成正⽐，因此提⾼信噪⽐必然要求我们减⼩射频带宽，射频带宽的减⼩导致较低的数据传输速率。

寻呼机的接收信噪⽐随着寻呼机与基站距离的增加⽽减⼩。

若将寻呼系统的覆盖范围⽤寻呼机正确接收所需的最低信噪⽐门限来表⽰，那么为了得到更好的覆盖，可以通过降低噪声功率来使得信噪⽐满⾜门限限制，即降低频带宽度（使得速率降低）。

2、假设蜂窝电话使⽤容量为1安培⼩时的电池。

假设蜂窝电话在空闲时耗电35mA ，通话时耗电250mA 。

如果⽤户⼀直开机，并且每天通话3分钟，那么这个电池能⽤多久？每天通话6⼩时呢？该电池最多能通话多久。

答：每天通话三分钟，则每天耗电：35*（24-3/60）+250*3/60=850.75mAh ，故可⽤1000/850.75=1.175天=28.21⼩时每天通话6⼩时，则每天耗电：35*18+250*6=2130mAh>1000mAh ，故⼀天不能通话6⼩时，最长通话时间为：1000/250=4⼩时。

移动通信原理习题Chapter 31、证明对六边形系统，同频复⽤因⼦为Q =3N ,其中22N i j ij =++.答：如图，由余弦定理：RD2、⼀个FDD 蜂窝电话系统分配有24MHz 总带宽，并使⽤两个30kHz 信道来提供全双⼯语⾳和控制信道。

设每个⼩区电话⽤户的业务量为0.1 Erlang 。

假设使⽤Erlang B 公式。

()2222222233222232cos12023333D i R j R i j R i j ij R NR =??+?? ? ?-??? ???=++=233DNRQ N R R===（a ）计算在4⼩区复⽤系统中每个⼩区的信道数。

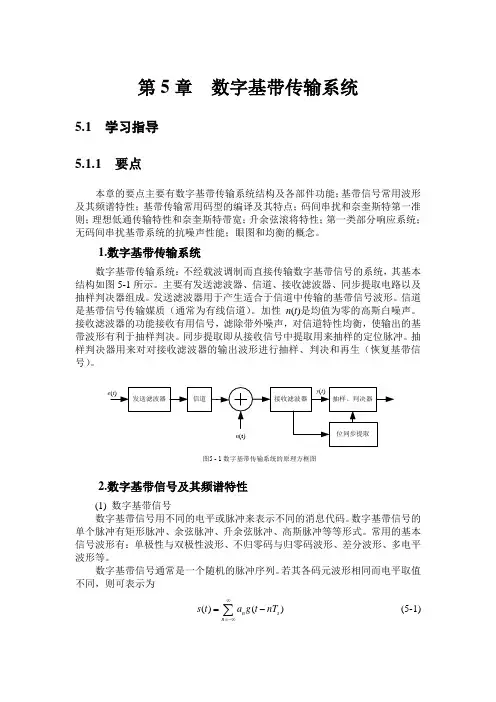
第5章 数字基带传输系统5.1 学习指导 5.1.1 要点本章的要点主要有数字基带传输系统结构及各部件功能；基带信号常用波形及其频谱特性；基带传输常用码型的编译及其特点；码间串扰和奈奎斯特第一准则；理想低通传输特性和奈奎斯特带宽；升余弦滚将特性；第一类部分响应系统；无码间串扰基带系统的抗噪声性能；眼图和均衡的概念。

1.数字基带传输系统数字基带传输系统：不经载波调制而直接传输数字基带信号的系统，其基本结构如图5-1所示。

主要有发送滤波器、信道、接收滤波器、同步提取电路以及抽样判决器组成。

发送滤波器用于产生适合于信道中传输的基带信号波形。

信道是基带信号传输媒质（通常为有线信道）。

加性n (t )是均值为零的高斯白噪声。

接收滤波器的功能接收有用信号，滤除带外噪声，对信道特性均衡，使输出的基带波形有利于抽样判决。

同步提取即从接收信号中提取用来抽样的定位脉冲。

抽样判决器用来对对接收滤波器的输出波形进行抽样、判决和再生（恢复基带信号）。

图5 - 1 数字基带传输系统的原理方框图发送滤波器信道接收滤波器抽样、判决器e (t )n (t)位同步提取y (t )2.数字基带信号及其频谱特性(1) 数字基带信号数字基带信号用不同的电平或脉冲来表示不同的消息代码。

数字基带信号的单个脉冲有矩形脉冲、余弦脉冲、升余弦脉冲、高斯脉冲等等形式。

常用的基本信号波形有：单极性与双极性波形、不归零码与归零码波形、差分波形、多电平波形等。

数字基带信号通常是一个随机的脉冲序列。

若其各码元波形相同而电平取值不同，则可表示为()()nsn s t a g t nT ∞=-∞=-∑ (5-1)式(5-1)中，a n 是第n 个码元所对应的电平值（随机量）；T s 为码元持续时间；g (t )为某种脉冲波形。

一般情况下，数字基带信号可表示为()()nn s t s t ∞=-∞=∑ (5-2)(2) 基带信号的频谱特性数字基带信号s (t )的频谱特性可以用功率谱密度来描述。

第五章（正弦载波数字调制系统）习题及其答案【题5－1】设发送数字信息为 011011100010，试分别画出 2ASK 、2FSK 、2PSK 及2DPSK 信号的波形示意图。

【答案5－1】2ASK 、2FSK 、2PSK 及2DPSK 信号的波形如下图所示。

【题5－2】已知某2ASK 系统的码元传输速率为103Band ，所用的载波信号为()6cos 410A π⨯。

1）设所传送的数字信息为011001，试画出相应的2ASK 信号波形示意图；2）求2ASK 信号的带宽。

【答案5－2】1）由题中的已知条件可知310B R Baud =因此一个码元周期为3110s B T s R -==载波频率为664102102s f Hz ππ⨯==⨯载波周期为61102T s -=⨯所以一个码元周期内有2000个载波周期。

如下图所示我们画出2ASK 信号的波形图，为简便，我们用两个载波周期代替2000个载波周期。

2）根据2ASK 的频谱特点，可知其带宽为222000B B R Hz T ===【题5－3】设某2FSK 调制系统的码元传输速率为1000Baud ，已调信号的载频为1000Hz 或 2000 HZ 。

1）若发送数字信息为011010，试画出相应的ZFSK 信号波形；2）试讨论这时的2FSK 信号应选择怎样的解调器解调？3）若发送数字信息是等可能的，试画出它的功率谱密度草图。

【答案5－3】1）由题意可画出ZFSK 信号波形如下图所示。

2）由于ZFSK 信号载波频差较小，频谱有较大重叠，采用非相干解调时上下两个支路有较大串扰，使解调性能降低。

由于两个载频人与人构成正交信号，采用相干解调可减小相互串扰，所以应采用相干解调。

3）该2FSK 信号功率谱密度草图如下图所示。

【题5－4】假设在某2DPSK 系统中，载波频率为 2400 Hz ，码元速率为 1200 Band ，已知相对码序列为11000101ll 。

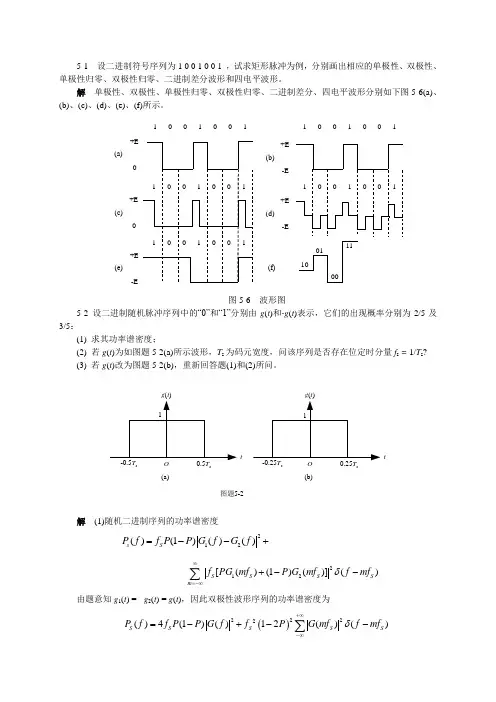
5-1 设二进制符号序列为1 0 0 1 0 0 1 ，试求矩形脉冲为例，分别画出相应的单极性、双极性、单极性归零、双极性归零、二进制差分波形和四电平波形。

解 单极性、双极性、单极性归零、双极性归零、二进制差分、四电平波形分别如下图5-6(a)、(b)、(c)、(d)、(e)、(f)所示。

图5-6 波形图5-2 设二进制随机脉冲序列中的“0”和“1”分别由g (t )和-g (t )表示，它们的出现概率分别为2/5及3/5：(1) 求其功率谱密度；(2) 若g (t )为如图题5-2(a)所示波形，T s 为码元宽度，问该序列是否存在位定时分量f s = 1/T s ? (3) 若g (t )改为图题5-2(b)，重新回答题(1)和(2)所问。

图题5-2g (t )sst(a)g (t )sst(b)解 (1)随机二进制序列的功率谱密度212()(1)()()s S P f f P P G f G f =--+212[()(1)()]()S S S S m f PG mf P G mf f mf δ∞=-∞+--∑由题意知g 1(t ) = - g 2(t ) = g (t )，因此双极性波形序列的功率谱密度为()2222()4(1)()12()()S S S S S P f f P P G f f P G mf f mf δ+∞-∞=-+--∑222241()()()2525S S S S f G f f G mf f mf δ+∞-∞=+-∑式中，G (f )⇔g (t )；等式右端第一项是连续谱成分，第二项是离散谱成分。

功率()SS P f df ∞-∞==⎰()22224(1)()12()()SS SSfP P G f df f P G mff mfdf δ∞∞∞-∞-∞-∞-+--∑⎰⎰222241(1)()()2525S S S f P P G f df f G mf ∞∞-∞-∞=-+∑⎰ (2)若基带脉冲波形g (t )为()1,20,ST t g t ⎧≤⎪=⎨⎪⎩其他则g (t )的傅里叶变换G (f )为()()S S G f T Sa T f π=因为sin ()()0s S S s SG f T Sa T f T πωπ===所以由题（1）的结果可知，该二进制序列不存在离散分量1/s s f T =。

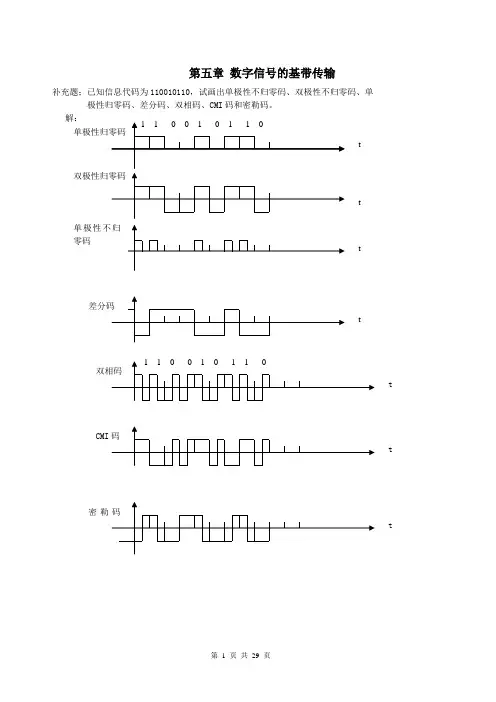
i 第五章测试 一 单选题（5*3）1、A 律13折中， 逐次比较编码后的结果送到译码器解码，解码后的结果和编码后的结果（经过7/11变换）比较，下列关系哪个是对的：a 、相等b 、大于c 、小于d 、以上都不对 (d)2、一个频带限制在0到f x 以内的低通信号x(t)，用f s 速率进行理想抽样，若要不失真的恢复x(t)，要求f s 与f x 关系满足：a 、b 、c 、d 、 (a)3 、对于ΔM 编码过程，过载量化噪声通常发生在：a 、信号幅值较大时b 、信号频率较大时c 、噪声较大时d 、信号斜率较大时 （d ）4 、以奈奎斯特速率进行抽样得到的以下抽样信号，仅用理想低通滤波器不可能将原始信号恢复出来的是。

a 、自然抽样b 、曲顶抽样c 、理想抽样d 、平顶抽样 （d ）5、PCM 均匀量化信噪比随着________增大而增大。

a 、量化级数b 、量化台阶c 、噪声功率d 、采样频率 （a ）二 计算题：（85分）1、对输入的正弦信号分别进行PCM 和ΔM 编码，要求在PCM 中进行均匀量化，量化级为Q ，在ΔM 中量化台阶σ和抽样频率fs 的选择保证不过载：(20分)（1）分别求出PCM 和ΔM 的最小实际比特率；（2）若两者的比特率相同，确定量化台阶σ的取值。

（1）PCM 最小比特速率为Q f Q f R m s B 222log log ⨯=⨯=（4分）在ΔM 中不过载要求：()s f dt t dx σ≤max 也就是σωσωmm s s m m A f f A ≥≤ΔM 中，每采样一次对应一个bit( 1 或 0) ,因此ΔM 输出比特率等于采样速率故ΔM 最小比特速率为：σωmm B A R =（2）根据题意可知Qf m 22log ⨯σωmm A =可得：QA Q f A mm m m 222log log πωσ==2、设简单增量调制系统的量化台阶σ＝50mV ，抽样频率为32kHz ，求当输入信号为800 Hz正弦波时，信号振幅动态范围。

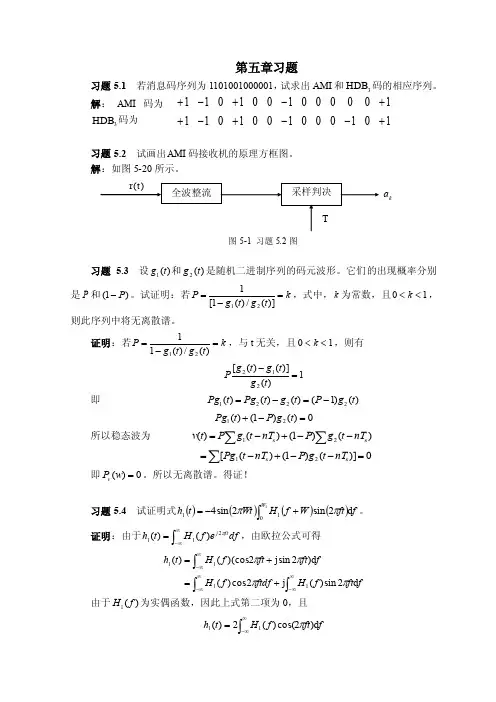
第五章习题习题5.1 若消息码序列为1101001000001，试求出AMI 和3HDB 码的相应序列。

解： AMI 码为 3HDB 码为习题5.2 试画出AMI 码接收机的原理方框图。

解：如图5-20所示。

图5-1 习题5.2图习题 5.3 设)(1t g 和)(2t g 是随机二进制序列的码元波形。

它们的出现概率分别是P 和)1(P -。

试证明：若k t g t g P =-=)](/)(1[121，式中，k 为常数，且10<<k ，则此序列中将无离散谱。

证明：若k t g t g P =-=)(/)(1121，与t 无关，且10<<k ，则有1)()]()([212=-t g t g t g P即 )()1()()()(2221t g P t g t Pg t Pg -=-=0)()1()(21=-+t g P t Pg所以稳态波为 ∑∑--+-=)()1()()(s 2s 1nT t g P nT t g P t v0)]()1()([s 2s 1=--+-=∑nT t g P nT t g P即0)(=w P v 。

所以无离散谱。

得证！习题5.4 试证明式()()()()⎰+-=1011d 2sin 2sin 4W f ft W f H Wt t h ππ。

证明：由于⎰∞∞-=df e f H t h ft j π211)()(，由欧拉公式可得⎰⎰⎰∞∞-∞∞-∞∞-+=+=fft f H ftdf f H fft ft f H t h d 2sin )(j 2cos )(d )2sin j 2)(cos ()(1111ππππ由于)(1f H 为实偶函数，因此上式第二项为0，且⎰∞∞-=f ft f H t h d )2cos()(2)(11π10100010010111000001001011+--+-++-+-+k a《通信原理》习题第五章令，'d d ,'f f W f f =+=，代入上式得⎰⎰⎰∞-∞-∞-+++=++=WWW fWt ft W f H f Wt ft W f H f t W f W f H t h d 2sin 2sin )(2d 2cos 2cos )(2'd ])'(2cos[)'(2)(1111πππππ由于)(1f H 单边为奇对称，故上式第一项为0，因此⎰⎰+=+=∞-WW fftt W f H W fftt W f H W t h 0111d 2sin )(2sin 4d 2sin )(2sin 2)(ππππ习题5.5 设一个二进制单极性基带信号序列中的“1”和“0”分别用脉冲)(t g [见图5-2的有无表示，并且它们出现的概率相等，码元持续时间等于T 。

5-2 解 (1)随机二进制序列的双边功率谱密度为由得式中，是的频谱函数，在功率谱密度中,第一部分是连续谱成分，第二部分是离散谱成分。

随机二进制序列的功率为（2）当基带脉冲波形为的付式变换为因为所以该二进制序列不存在离散分量。

（3）当基带脉冲波形为的付式变换为因为所以该二进制序列存在离散分量。

5-3 解（ 1）由图 5-7 得的频谱函数为由题意且所以代入二进制数字基带信号的双边功率谱密度函数式,可得(2) 二进制数字基带信号的离散谱分量为当代入上式得因为该二进制数字基带信号中存在离散谱分量，所以能从该数字基带信号中提取码元同步所取得频率的分量。

该频率分量的功率为5-6解 AMI 码为+10-1+1000000000-10+1HDB3 码+10-1+1000+V –B00 –V0+10-15-7解 PST码为 -++0+--+0-+0-++-双相码为01 0110 01 10 10 01 01 01 10 10 01 01 01 10 105-8解原信息代码为 1010000100001100001015-9解（ 1）令由图 5-8 可得，因为的频谱函数为所以，系统的传输函数为（2）系统的传输函数由发送滤波器，信道和接收滤波器三部分组成，即因为则所以，发送滤波器和接收滤波器为5-10 解（ 1）总特性 H（ f）可以看成是图 5-11 两个三角形特性之差，即H （ f ） =H1 （ f） -H2（ f ）其中 H 1 ( f )h1 (t )1(1)W1 gSa2(1)Wt112H 2 ( f )h2(t )(1)W1gSa2(1)W1t2h(t )h1 (t )h2 (t)所以冲激响应(1)2W1 gSa2(1)2(1)Wt`W1gSa2(1 )Wt`22（2）因为该系统克等小成理想低通特性H eq ( f )1,f W1 0,f W1它所对应的无码间串扰的最高传码率为2W1，所当传输速率为2W1 时，在抽样店无码间串扰。

通信原理第七版课后答案樊昌信(总57页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章习题习题 在英文字母中E 出现的概率最大，等于，试求其信息量。

解：E 的信息量：()()b 25.3105.0log E log E 1log 222E =-=-==P P I习题 某信息源由A ，B ，C ，D 四个符号组成，设每个符号独立出现，其出现的概率分别为1/4，1/4，3/16，5/16。

试求该信息源中每个符号的信息量。

解：b A P A P I A 241log )(log )(1log 222=-=-==b I B 415.2163log 2=-= b I C 415.2163log 2=-= b I D 678.1165log 2=-=习题 某信息源由A ，B ，C ，D 四个符号组成，这些符号分别用二进制码组00，01，10，11表示。

若每个二进制码元用宽度为5ms 的脉冲传输，试分别求出在下列条件下的平均信息速率。

（1）这四个符号等概率出现； （2）这四个符号出现概率如习题所示。

解：（1）一个字母对应两个二进制脉冲，属于四进制符号，故一个字母的持续时间为2×5ms。

传送字母的符号速率为Bd 100105213B =⨯⨯=-R 等概时的平均信息速率为s b 2004log log 2B 2B b ===R M R R（2）平均信息量为符号比特977.1516log 165316log 1634log 414log 412222=+++=H则平均信息速率为 s b 7.197977.1100B b =⨯==H R R习题 试问上题中的码元速率是多少 解：311200 Bd 5*10B B R T -===习题 设一个信息源由64个不同的符号组成，其中16个符号的出现概率均为1/32，其余48个符号出现的概率为1/96，若此信息源每秒发出1000个独立的符号，试求该信息源的平均信息速率。

第五章 数字基带传输系统第六章\设随机二进制序列中的0和1分别由g （t ）和-g （t ）组成，它们的出现概率分别为P 及（1-P ）：求其功率谱密度及功率；解：（1）随机二进制序列的双边功率谱密度为P s (ω)=f s P(1-P)|G 1(f)-G 2(f)|2 + ∑|f s [PG 1(mf s ) + (1-P)G 2(mf s )]|2δ(f- mf s ) 由g 1(t)=-g 2(t)=g(t)得P s (ω)=4f s P(1-P)G 2(f) + f s (1-2P)2∑|G(mf s )|2δ(f- mf s )式中，G(f)是g （t ）的频谱函数，在功率谱密度P s (ω)中，第一部分是其连续谱部分，第二部分是其离散成分。

随机二进制序列的功率为 S=1/2л∫P s (ω)d ω=4f s P(1-P)∫G 2(f)df + ∑|f s (1-2P) G(mf s )|2∫δ(f- mf s )df =4f s P(1-P)∫G 2(f)df + f s P(1-P)2∑|G(mf s )|2 (2)当基带脉冲波形g(t)为⎪⎩⎪⎨⎧≤=t T t t g s 其他,02||,1)(g(t)的傅立叶变换G(f)为s ssfT fT T f G ππsin )(=因为0sin )(==ss ss sT f T f T f G ππ由题（1）中的结果知，此时的离散分量为0。

（3）⎪⎩⎪⎨⎧≤=t T t t g s 其他,04||,1)(g （t ）的傅立叶变换G （f ）为2/2/sin 2)(≠==πππss s s s s T T f T f T f G所以该二进制序列存在离散分量s sT f 1=1. 设某二进制数字基带信号的基本脉冲为三角形脉冲，如图所示。

图中s T 为码元间隔，数字信号“1”和“0”分别用g(t)的有无表示，且“1”和“0”出现的概率相等：（1） 求该数字基带信号的功率谱密度，并画出功率谱密度图；（2）能否从该数字基带信中提取码元同步所需的频率ss T f 1=的分量，若能，式计算该分量的功率。

第5章习题解答1. 已知某2ASK 系统的码元速率为1000波特，所用载波信号为()6cos 410A t π⨯。

（1） 假定比特序列为{0110010}，试画出相应的2ASK 信号波形示意图； （2） 求2ASK 信号第一零点带宽。

解：由1000b sR R bps ==，6210c f Hz =⨯， 621020001000b c c b T f T R ⨯===（1）一个码元周期内有2000个正弦周期：111{}n a ()2ASK s t 0（2）022000b B R Hz ==2. 某2ASK 系统的速率为2b R =Mbps ，接收机输入信号的振幅40μV A =，AWGN 信道的单边功率谱密度为180510N -=⨯W/Hz ，试求传输信号的带宽与系统的接收误码率。

解：传输信号的带宽24T b B R MHz ==，平均码元能量：24bb A T E =。

()()22212010cos 21cos 4,0222b bT T bb c c b b b b A T A E A f t dt f t dt E E E E ππ==+==+=⎰⎰系统的接收误码率： （1）若是非相干解调，()2622618000401040444210510b b b E A T AN N R N --⨯====⨯⨯⨯⨯ 由非相干解调误码率公式，/4092211 1.03061022b E N e P ee ---≈==⨯ （2）若是相干解调：由相干解调误码率公式得，101.269810b P Q Q-===⨯3. 某2FSK 发送“1”码时，信号为()()111sin s t A t ωθ=+，0s t T ≤≤；发送“0”码时，信号为()()000sin s t A t ωθ=+，0s t T ≤≤。

式中1θ及0θ为均匀分布随机变量，0128s ωωπ==，“1”与“0”码等概率出现。

（1） 画出包络检波形式的接收机框图； （2） 设码元序列为11010，画出接收机中的主要波形（不考虑噪声）；（3） 若接收机输入高斯噪声功率谱密度为02N （W/Hz ），试给出系统的误码率公式。

习题5-1 设待发送的数字序列为10110010，试分别画出2ASK 、2FSK 、2PSK 和2DPSK 的信号波形。

已知在2ASK 、2PSK 和2DPSK 中载频为码元速率的2倍；在2FSK 中，0码元的载频为码元速率的2倍，1码元的载频为码元速率的3倍。

解：波形略5-2 已知某2ASK 系统的码元传输速率为1200B ，采用的载波信号为A cos(48π⨯102t )，所传送的数字信号序列为101100011：（1）试构成一种2ASK 信号调制器原理框图，并画出2ASK 信号的时间波形； （2）试画出2ASK 信号频谱结构示意图，并计算其带宽。

解：（1）2ASK 信号调制器原理框图如图5.2.1-2，2ASK 信号的时间波形略。

（2）2ASK 信号频谱结构示意图如图5.2.1-5，则其带宽为B 2ASK =2f s ＝2400Hz 。

5-3 若对题5-2中的2ASK 信号采用包络检波方式进行解调，试构成解调器原理图，并画出各点时间波形。

解：2ASK 信号采用包络检波的解调器原理图：cos ωc t(t )(a )图5.2.1-2 2ASK 信号调制原理框图(b )(t )开关电路图5.2.1-5 2ASK 信号的功率谱e各点时间波形：（下图对应各点要换成101100011）5-4 设待发送的二进制信息为1100100010，采用2FSK 方式传输。

发1码时的波形为A cos(2000π t +θ1)，发0码时的波形为A cos(8000π t +θ0)，码元速率为1000B ：（1）试构成一种2FSK 信号调制器原理框图，并画出2FSK 信号的时间波形； （2）试画出2FSK 信号频谱结构示意图，并计算其带宽。

解：（1）2FSK 信号调制器原理框图如下图，时间波形略。

（2）2FSK 信号频谱结构示意图如下图，其带宽221240001000210005000FSK s B f f f Hz =-+=-+⨯=。

第五章5-1 已知线性调制信号表示式如下：（1）ttcωcoscosΩ，（2）tc5.01(+。

式中，Ω=6cω。

试分别画出它们的波形图和频谱图。

5-2 根据图P5-1所示的调制信号波形，试画出DSB及AM信号的波形图，并比较它们分别通过包络检波器后的波形差别。

解：5-3已知调制信号m(t)=cos(2000πt)+ cos(4000πt)，载波为cos104πt，进行单边带调制，试确定该单边带信号的表示式，并画出频谱图。

5-4 将调幅波通过残留边带滤波器产生残留边带信号。

若此滤波器的传输函数H(ω)如图P5-2所示（斜线段为直线）。

当调制信号为f/kHz)解：设调幅波[()]cosAM cs m m t tω=+，其中()m m t，且()AM DSBs Sω⇔，根据残留边带滤波器在cω处的互补对称性，从()Hω的图中得知载频cf为10kHz，由此得到载波cos20000tπ。

因此设残留边带信号为()VSBs t，且()()VSB VSBs t Sω⇔，则()()()VSB DSBs t S Hωω⇔。

由图5-3可得10.05f kHz=±时，()10.059.50.55Hω=-=；10f kHz=±时，()0.5Hω=；9.95f kHz=±时，()9.959.50.45Hω=-=；7f kHz=±时，()0Hω=。

故5-5 某调制方框图如图P5-3（b）所示。

已知()m t的频谱如图P5-3（a）所示，载频12ωω，1Hωω>，且理想低通滤波器的截止频率为1ω，试求输出信号()s t，并说明()s t为何种已调信号。

解：上支路输入信号()m t 与1cos t ω相乘产生DSB 信号（频谱的中心频率为1ω），经过理想低通滤波器（截止频率1ω）后，产生下下边带信号输出：下支路输入信号()m t 与1sin t ω相乘产生DSB 信号（频谱的中心频率为1ω），经过理想低通滤波器（截止频率1ω）后，产生另一个下边带信号输出：1()s t 与2()s t 分别与2cos t ω和2sin t ω相乘，再相加后的输出信号11211211()[()cos ()sin ]cos [()sin ()cos ]sin 22s t m t t m t t t m t t m t t t ωωωωωω=++- 即：()s t 为载频为21ωω-的上边带信号。

第五章习题习题5.1 若消息码序列为1101001000001，试求出AMI 和3HDB 码的相应序列。

解： A MI 码为 3HDB 码为习题5.2 试画出A MI 码接收机的原理方框图。

解：如图5-20所示。

图5-1 习题5.2图习题 5.3 设)(1t g 和)(2t g 是随机二进制序列的码元波形。

它们的出现概率分别是P 和)1(P -。

试证明：若k t g t g P =-=)](/)(1[121，式中，k 为常数，且10<<k ，则此序列中将无离散谱。

证明：若k t g t g P =-=)(/)(1121，与t 无关，且10<<k ，则有1)()]()([212=-t g t g t g P即 )()1()()()(2221t g P t g t Pg t Pg -=-=0)()1()(21=-+t g P t Pg所以稳态波为 ∑∑--+-=)()1()()(s 2s 1nT t g P nT t g P t v0)]()1()([s 2s 1=--+-=∑nT t g P nT t g P即0)(=w P v 。

所以无离散谱。

得证！习题5.4 试证明式()()()()⎰+-=1011d 2sin 2sin 4W f ft W f H Wt t h ππ。

证明：由于⎰∞∞-=df e f H t h ft j π211)()(，由欧拉公式可得⎰⎰⎰∞∞-∞∞-∞∞-+=+=fft f H ftdf f H fft ft f H t h d 2sin )(j 2cos )(d )2sin j 2)(cos ()(1111ππππ由于)(1f H 为实偶函数，因此上式第二项为0，且⎰∞∞-=f ft f H t h d )2cos()(2)(11π10100010010111000001001011+--+-++-+-+k a令，'d d ,'f f W f f =+=，代入上式得⎰⎰⎰∞-∞-∞-+++=++=WWW fWt ft W f H f Wt ft W f H f t W f W f H t h d 2sin 2sin )(2d 2cos 2cos )(2'd ])'(2cos[)'(2)(1111πππππ由于)(1f H 单边为奇对称，故上式第一项为0，因此⎰⎰+=+=∞-WW fftt W f H W fftt W f H W t h 0111d 2sin )(2sin 4d 2sin )(2sin 2)(ππππ习题5.5 设一个二进制单极性基带信号序列中的“1”和“0”分别用脉冲)(t g [见图5-2的有无表示，并且它们出现的概率相等，码元持续时间等于T 。