第7讲 树和二叉树讲解
- 格式:ppt
- 大小:2.12 MB
- 文档页数:52

信息学奥赛培训之『树——二叉树』树——二叉树为何要重点研究二叉树? 引 : 为何要重点研究二叉树 ? (1)二叉树的结构最简单,规律性最强; (2)可以证明,所有树都能转为唯一对应的二叉树,不失一般性。
一、二叉树基础1. 二叉树的定义 二叉树是一类非常重要的树形结构,它可以递归地定义如下: 二叉树 T 是有限个结点的集合,它或者是空集,或者由一个根结点以及分别称为左 子树和右子树的两棵互不相交的二叉树。
因此,二叉树的根可以有空的左子树或空的右子树,或者左、右子树均为空。
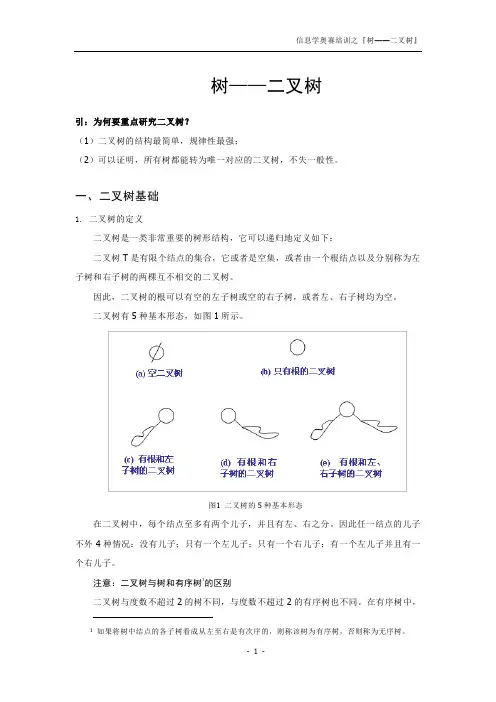
二叉树有 5 种基本形态,如图 1 所示。
图1 二叉树的 5 种基本形态在二叉树中,每个结点至多有两个儿子,并且有左、右之分。
因此任一结点的儿子 不外 4 种情况:没有儿子;只有一个左儿子;只有一个右儿子;有一个左儿子并且有一 个右儿子。
注意:二叉树与树和有序树 的区别 二叉树与度数不超过 2 的树不同,与度数不超过 2 的有序树也不同。
在有序树中,11如果将树中结点的各子树看成从左至右是有次序的,则称该树为有序树,否则称为无序树。
-1-信息学奥赛培训之『树——二叉树』虽然一个结点的儿子之间是有左右次序的,但若该结点只有一个儿子时,就无须区分其 左右次序。
而在二叉树中,即使是一个儿子也有左右之分。
例如图 2-1 中(a)和(b)是两棵 不同的二叉树。
虽然它们与图 2-2 中的普通树(作为无序树或有序树)很相似,但它们却 不能等同于这棵普通的树。
若将这 3 棵树均看作是有序树,则它们就是相同的了。
图2-1 两棵不同的二叉树图2-2 一棵普通的树由此可见,尽管二叉树与树有许多相似之处,但二叉树不是树的特殊情形。
不是 ..2. 二叉树的性质图3 二叉树性质1: 在二叉树的第 i 层上至多有 2 i −1 结点(i>=1)。
性质2: 深度为 k 的二叉树至多有 2 k − 1 个结点(k>=1)。
性质3: 对任何一棵二叉树 T,如果其终端结点数为 n0,度为 2 的结点数为 n2,则 n0=n2+1。



数据结构详细教案——树与二叉树一、教学目标1.了解树和二叉树的基本概念和特点;2.掌握树和二叉树的基本操作;3.能够通过递归遍历树和二叉树。
二、教学重难点1.树和二叉树的基本概念和特点;2.递归遍历树和二叉树。
三、教学内容1.树的概念和特点1.1树的定义树是n(n>=0)个节点的有限集。
当n=0时,称为空树;如果不为空树,则1. 树有且仅有一个特殊节点被称为根(Root);2.其余节点可分为m(m>0)个互不相交的有限集T1,T2,...,Tm,其中每个集合又是一棵树。
1.2节点间的关系- 父节点(parent)是当前节点的直接上级节点;- 子节点(child)是当前节点的直接下级节点;- 兄弟节点(sibling)是具有同一父节点的节点;- 祖先节点(ancestor)是通过从当前节点到根的任意路径可以到达的节点;- 子孙节点(descendant)是通过从该节点到子树的任意节点可以到达的节点。
1.3树的特点-树是一个有层次的结构,可以看作是一个鱼骨图;-树中的每个节点都可以有多个子节点,但只有一个父节点;-树中的节点之间是唯一的,不存在重复节点;-树中的任意两个节点之间都有且仅有一条路径连接。
2.二叉树的概念和特点2.1二叉树的定义二叉树是一种特殊的树结构,它的每个节点最多只能有两个子节点,分别称为左子节点和右子节点。
2.2二叉树的特点-二叉树的度最大为2,即每个节点最多有两个子节点;-二叉树的第i层最多有2^(i-1)个节点;-对于任意一颗二叉树,如果其叶子节点数为n0,度为2的节点数为n2,则有n0=n2+1;-完全二叉树是一种特殊的二叉树,除了最后一层的叶子节点外,每一层的节点都是满的。
四、教学过程1.讲解树和二叉树的基本概念和特点,引导学生理解树和二叉树的定义和节点间的关系。
2.分析树和二叉树的基本操作,并通过实例演示操作过程,让学生掌握操作的步骤和方法。
3.运用递归算法遍历树和二叉树的过程,详细讲解前序遍历、中序遍历和后序遍历的定义和实现方法。


树和二叉树知识考点整理●树的基本概念●树的定义●n个结点的有限集●n=0代表空树●满足条件●只有一个根的结点●其余结点是互不相交的有限集,每个集合本身是一棵树,是根的子树●树是一种递归的数据结构●树的根结点没有前驱,其余结点只有一个前驱●树中所有结点可以有零个或多个后驱●基本术语●双亲、兄弟、孩子、祖先●度:孩子个数●分支结点:度大于0●叶子结点:度为0●深度:从下往上;●高度:从上往下;●有序树:从左到右是有次序的●路径和路径长度:路径是从上往下的●森林:m棵互不相交的树的集合。
●树的基本性质●结点数=所有结点度数之和+1●度为m的树中第i层上至多有m的i-1次分个结点●高度为h的m叉树至多有(m^h-1)/(m-1)个结点●具有n个结点的m叉树的最小高度为「logm(n(m-1)+1)]●二叉树的概念●定义●一种树形结构,特点是每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点)并且二叉树的子树有左右之分,次序不可颠倒●二叉树与度为2的有序树区别●度为2的可以有三个结点,二叉树可以是空树●度为2的有序树的孩子左右之分是根据另一个孩子而言的;二叉树无论有没有,都要确定左右●特殊的二叉树●满二叉树●树中每一层都含有最多的结点●完全二叉树●高度为h,有n个结点的二叉树,当且仅当,每个结点都与高度为h的满二叉树中的编号一一对应●二叉排序树●用途:可用于元素的排序、搜索●左子树上所有结点的关键字均小于根结点的关键字;右子树上所有结点的关键字均大于根结点的关键字;左子树和右子树又是一棵二叉排序树●二叉树的性质●非空二叉树上的叶子结点数等于度为2的结点树加1,即n0=n2+1●非空二叉树上第k层至多有2^(k-1)个结点●高度为h的二叉树至多有2^h-1个结点●具有n个结点的完全二叉树的高度为log2(n+1)取顶或者log2n取底+1●二叉树的存储结构●顺序存储结构●只适合存储完全二叉树,数组从0开始●链式存储结构●顺序存储的空间利用率太低●至少三个指针域:数据域、左指针域、右指针域●增加了指向父结点后,变为三叉链表的存储结构●在含有n个结点的二叉链表中,含有n+1个空链域●二叉树的遍历和线索二叉树●二叉树的遍历●先序遍历●根左右●应用:求树的深度●中序遍历●左根右●后序遍历●左右根●应用:求根到某结点的路径、求两个结点的最近公共祖先等●三个遍历时间复杂度都是O(n)●递归算法和非递归算法的转换●层次遍历●需要借助队列●步骤●二叉树根结点入队,然后出队,访问出队结点,若有左子树,左子树根结点入队●遍历右子树,有右子树,右子树根结点入队。

数据结构树和二叉树知识点总结
1.树的概念:树是一种非线性的数据结构,由节点和边构成,每个节点只能有一个父节点,但可以有多个子节点。
2. 二叉树的概念:二叉树是一种特殊的树结构,每个节点最多只有两个子节点,一个是左子节点,一个是右子节点。
3. 二叉树的遍历:二叉树的遍历分为前序遍历、中序遍历和后序遍历三种方式。
前序遍历是先访问根节点,再访问左子树,最后访问右子树;中序遍历是先访问左子树,再访问根节点,最后访问右子树;后序遍历是先访问左子树,再访问右子树,最后访问根节点。
4. 二叉搜索树:二叉搜索树是一种特殊的二叉树,它满足左子树中所有节点的值均小于根节点的值,右子树中所有节点的值均大于根节点的值。
因此,二叉搜索树的中序遍历是一个有序序列。
5. 平衡二叉树:平衡二叉树是一种特殊的二叉搜索树,它的左子树和右子树的高度差不超过1。
平衡二叉树的插入和删除操作可以保证树的平衡性,从而提高树的查询效率。
6. 堆:堆是一种特殊的树结构,它分为最大堆和最小堆两种。
最大堆的每个节点的值都大于等于其子节点的值,最小堆的每个节点的值都小于等于其子节点的值。
堆常用于排序和优先队列。
7. Trie树:Trie树是一种特殊的树结构,它用于字符串的匹配和检索。
Trie树的每个节点代表一个字符串的前缀,从根节点到叶子节点的路径组成一个完整的字符串。
以上是数据结构树和二叉树的一些基本知识点总结,对于深入学
习数据结构和算法有很大的帮助。


树、⼆叉树、满⼆叉树、完全⼆叉树概念分清⾃由树⾃由树是⼀个连通的,⽆回路的⽆向图。
令G=(V,E)为⼀个⽆向图。
下⾯的表述是等价的。
1) G是⾃由树。
2) G中任意两个顶点由唯⼀⼀条简单路径得到。
3) G是连通的,但从E中去掉任何边后得到的图都是⾮连通的。
4) G是⽆回路的,且|E|=|V|-1。
5) G是连通的,且|E|=|V|-1。
6) G是⽆回路的,但添加任何边到E中得到的图包含回路。
⼆叉树在计算机科学中,⼆叉树是每个节点最多有两个⼦树的树结构。
通常⼦树被称作“左⼦树”(left subtree)和“右⼦树”(right subtree)。
⼆叉树的每个结点⾄多只有⼆棵⼦树(不存在度⼤于2的结点),⼆叉树的⼦树有左右之分,次序不能颠倒。
⼆叉树的第i层⾄多有2^(i-1)个结点;深度为k的⼆叉树⾄多有2^k-1个结点;(等⽐数列1+2+4+…+2^(k-1) = 2^k-1)。
对任何⼀棵⼆叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0 = n2 + 1。
树和⼆叉树的三个主要差别:1) 树的结点个数⾄少为1,⽽⼆叉树的结点个数可以为0;2) 树中结点的最⼤度数没有限制,⽽⼆叉树结点的最⼤度数为2;3) 树的结点⽆左、右之分,⽽⼆叉树的结点有左、右之分。
满⼆叉树⼀棵深度为k,且有2^k-1个节点的树是满⼆叉树。
另⼀种定义:除了叶结点外每⼀个结点都有左右⼦叶且叶⼦结点都处在最底层的⼆叉树。
这两种定义是等价的。
从树的外形来看,满⼆叉树是严格三⾓形的,⼤家记住下⾯的图,它就是满⼆叉树的标准形态:所有内部节点都有两个⼦节点,最底⼀层是叶⼦节点。
性质:1) 如果⼀颗树深度为h,最⼤层数为k,且深度与最⼤层数相同,即k=h;2) 它的叶⼦数是: 2^(h-1)3) 第k层的结点数是: 2^(k-1)4) 总结点数是: 2^k-1 (2的k次⽅减⼀)5) 总节点数⼀定是奇数。
6) 树⾼:h=log2(n+1)。
教学过程一、导入树是一类重要的非线性数据结构,是以分支关系定义的层次结构。
在日常生活同学们经常见到树。
树有一个树根。
有许多树枝,在树枝上长有很多树叶。
就象我们今天要讲的树,是一种层次结构。
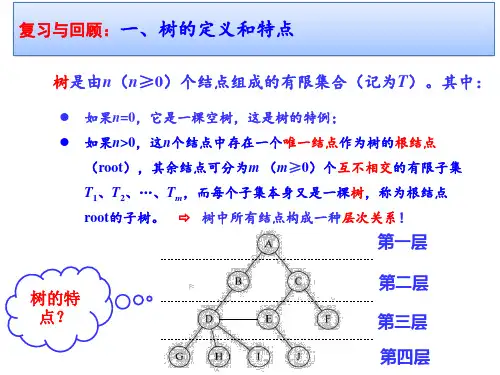
二、新授(一)树1.树的定义树(tree)是由n (n≥0) 个结点组成的有限集合。
它是树型结构的简称,是一种重要的非线性数据结构,应用广泛。
如:磁盘上的文件目录结构、家族成员关系、单位的组织机构、书的内容组织、算术表达式等。
任何一棵非空树是一个二元组:Tree = (root,F)其中:root被称为根结点,F被称为子树森林2.基本术语森林:是m(m≥0)棵互不相交的树的集合有向树:有确定的根,树根和子树根之间为有向关系(自上到下,自左到右)有序树:树中结点的各子树从左到右是有次序的,不能互换无序树:树中结点的各子树从左到右是没有次序的子女:结点的子树的根是该结点的孩子双亲:孩子结点的根结点兄弟:具有同一双亲的结点堂兄弟:双亲在同一层的结点祖先:从根到该结点所经历分支上的所有结点子孙:以某结点为根的子树中的任一结点学生活动:请同学门总结树形与线形的异同(二) 二叉树1.二叉树的定义二叉树(BinaryTree)是n(n≥0)个结点的有限集,它或者是空集(n=0),或者由一个根结点及两棵互不相交的、分别称作这个根的左子树和右子树的二叉树组成。
2.二叉树的五种基本形态二叉树可以是空集;根可以有空的左子树或右子树;或者左、右子树皆为空。
3.二叉树不是树的特例(1)二叉树与无序树不同二叉树中,每个结点最多只能有两棵子树,并且有左右之分。
二叉树并非是树的特殊情形,它们是两种不同的数据结构。
(2)二叉树与度数为2的有序树不同在有序树中,虽然一个结点的孩子之间是有左右次序的,但是若该结点只有一个孩子,就无须区分其左右次序。
而在二叉树中,即使是一个孩子也有左右之分。
4、满二叉树和完全二叉树是二叉树的两种特殊情形。
a、满二叉树一棵深度为k且有2k-1个结点的二又树称为满二叉树。