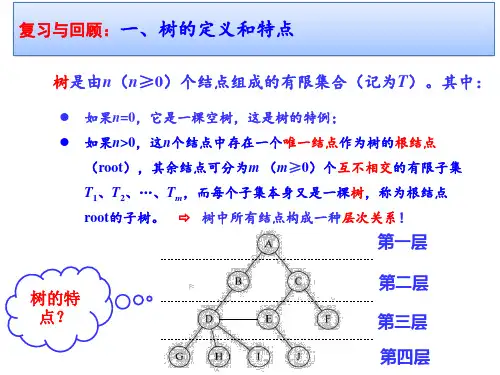
第七章 树

（root），其余结点可分为m （m≥0）个互不相交的有限子集 T1、T2、…、Tm，而每个子集本身又是一棵树，称为根结点 root的子树。 树中所有结点构成一种层次关系！
第一层
树的特 点？
第二层 第三层 第四层
复习：二、树的基本术语
1.结点A、D的度？树的度？ 2;3;3; 2.根结点？分支结点？叶子结点？ A;BCDE;GHIJF;
在二叉链中，空指针的个数？
b A
B∧
C
∧D
∧E∧
∧F∧
∧G∧
n个结点 2n个指针域 分支数为n-1 非空指针域有n-1个 空指针域个数 = 2n-(n-1) = n+1
n=7 空指针域个数=8
39/10
40/10
二叉树
当n=3，结果为ห้องสมุดไป่ตู้。
第n个Catalan数
41/23
有n个结点并且高度为n的不同形态的二叉树个数是多少？ 该二叉树：有n层，每层一个结点，该结点可以
43/23
结点个数为n，树形可以唯一确定 叶子结点个数为n0，树形不能唯一确定 n为奇数时，n1=0； n为偶数时，n1=1。 n0=n2+1 高度h= log2(n+1)，是n个结点高度最小的二叉树
44/23
含有60个叶子结点的二叉树的最小高度是多少？
在该二叉树中，n0=60，n2=n0-1=59，n=n0+n1+n2=119+n1。 当n1=0且为完全二叉树时高度最小。 此时高度h=log2(n+1)= log2120=7。
作为双亲结点的左孩子，也可以作为右孩子 这样的二叉树的个数=1×2×…×2=2n-1。
例如，当n=3时有22=4个这样的二叉树。

第七章 树木生长量测定习题一、填空题1．施耐德材积生长率的公式为 ，式中 。

2．树木生长包括 、 、 基本过程。

3．Logistic 方程 、Gompertz 方程 和单分子式 。

4．树木生长量分为 、 、 、 、 等五类。

5．某解析木长7.9米，用一米区分段区分，则梢头长度是 米。

6．一定期间内某调查因子的生长量即为 生长量。

7．总平均生长量是 被 所除之商。

8．典型的树木总生长量曲线是呈 形。

9．树木生长率是某调查因子的 生长量与 的百分比。

10．测定树干材积的三要素 、 、 。

二、名词解释1．树木的生长方程2．理论生长方程3．树干解析4．普雷斯勒生长率公式5．定期平均生长量三、简答题1．Richards 生长方程的生物学假设。

2．简述树木生长的特点。

3．简述树木年龄的测定方法。

4．树木连年生长量和平均生长量之间的关系。

四、论述题1．推导说明Mistcherlich （单分子式）生长方程（)1(kt e A y --=式中：A ，k 为方程参数；y 为林木大小；t 为年龄）性质，并说明其适用于描述何种生长曲线类型。

2．推导说明理查德生长方程（c kt e A y )1(--=式中：A,k,c 为方程参数；y 为林木大小；t 为年龄）性质，并说明其适用于描述何种生长曲线类型。

五、证明题1．推导Gompertz 生长方程,并讨论其性质。

2．树木的生长率与时间平方的倒数成正比，试推导该生长方程，并讨论其性质。

(提示：请代入边界条件求特解)六、计算题1．某一树高3年,6年和9年时的总生长量分别为1.2cm,2.6cm,5.0cm, 试求各龄阶平均生长量及连年生长量。

2．有两株树做树干解析（按等长区分），一株H=29.3米，一株H=8.7米，问各树梢底径位置及截取圆盘的个数。

3．一株落叶松人工林树高总生长方程为：t e H /64.185.32-= 试计算该树30年（t=30）时的树高连年生长量。

4．某一株树高3年和6年时的总生长量分别为1.0m ，2.6m ，试计算5年时的树高。

第一节
茶树优质高产树冠模式
三、茶树树冠培养的主要修剪方式
※ 用于幼年茶树和台刈后的茶树。 ※ 通过剪去部分主枝和高位侧枝控 制树高，培养健壮骨干枝，促进分 枝的合理布局和扩大树冠。 ※ 培养理想树冠需经几次定型修剪 才能完成，并通过轻修剪和打顶轻 采加以调整。
在整堂课的教学中，刘教师总是让学 生带着 问题来 学习， 而问题 的设置 具有一 定的梯 度，由 浅入深 ，所提 出的问 题也很 明确
4、利用枝条的异质性，更新复壮树冠
茶树形态学下部，从生长年龄来说是年长的， 但其生理发育年龄梯度是年幼的；茶树上部枝条则 相反。
修剪部位越低，阶段发育年龄轻，剪后开花就 迟，由基部长出的枝梢生育能力也较强。
在整堂课的教学中，刘教师总是让学 生带着 问题来 学习， 而问题 的设置 具有一 定的梯 度，由 浅入深 ，所提 出的问 题也很 明确
第一节
茶树优质高产树冠模式
（二）树冠高度适中
太矮，难达一定覆盖度和芽叶密度； 太高，降低了光合产物和矿质营养。
1、大叶种（高型树冠） 1m左右 ——热带、亚热带区域
2、中小叶种（中型树冠） 80-90cm ——长江流域
3、小叶种（低型树冠） 50-70cm ——江北茶区
在整堂课的教学中，刘教师总是让学 生带着 问题来 学习， 而问题 的设置 具有一 定的梯 度，由 浅入深 ，所提 出的问 题也很 明确
在整堂课的教学中，刘教师总是让学 生带着 问题来 学习， 而问题 的设置 具有一 定的梯 度，由 浅入深 ，所提 出的问 题也很 明确
第一节
茶树优质高产树冠模式
一、高产优质茶树树冠的构成
（一）分枝结构合理
1、分枝层次多且清楚 分枝层次可达12－14层

(b)
(a)
V5
2
1
V7
8
9
V2
V4
2
3
V8
5
V1
V1
V4
V5
1
3
V7
V6
8
V4
2
V8
5
6
V1
1
V5
6
V7
V6
8
3
V8
5
6
V7
9
V3
(e)
V3
(f)
(g)
22
V2
V3
(h)
五.应用举例——求最小生成树
例3 用管梅谷算法求下图的最小生成树。
23
五.应用举例——求最小生成树
例3 用管梅谷算法求下图的最小生成树。
成圈。
首先证明T无简单回路。对n作归纳证明。
(i) n=1时,m=n-1=0,显然无简单回路；
(ii)假设顶点数为n-1时无简单回路，现考察顶点数是n的情况：此时至少有一
个顶点v其次数d(v)=1。因为若n个顶点的次数都大于等于2，则不少于n条边，但这与
m=n-1矛盾。
删去v及其关联边得到新图T’，根据归纳假设T’无简单回路，再加回v及其关联
边又得到图T，则T也无简单回路。
再由图的连通性可知，加入任何一边后就会形成圈，且只有一个圈，否则原图
中会含圈。
9
二. 基本定理——证明
证明(4):(3)(4)，即证一个无圈图若加入任一边就形成圈，
则该图连通，且其任何一边都是桥。
若图不连通,则存在两个顶点vi和vj，在vi和vj之间没有路，若
加边(vi,vj)不会产生简单回路，但这与假设矛盾。由于T无简单回

4t中一个非叶子结点至少有一个孩子结点其中有一个最右边的孩子结点s在b中s没有右孩子t中n个非叶子结点b中对应n个没有右孩子结点t的根结点对应b的根结点它一定是没有右孩子结点n1523先根遍历后根遍历层次遍历具有递归性623给定一棵树t将其转换成二叉树b后t的先根遍历对应b的什么遍历序列
1
树
度为m的树中所有结点的度 ≤ m
5/23
先根遍历 后根遍历 层次遍历
具有递归性
6/23
给定一棵树T，将其转换成二叉树B后，T的先根遍历 对应B的什么遍历序列？
A A B
T
B
T2 T12
B
t11 t2
…
T11
…
t12
先根遍历：A B T11 T12 T2 …
先序遍历：A B t11 t12 t2 …
7/23
给定一棵树T，将其转换成二叉树B后，T的后 根遍历对应B的什么遍历序列？
10/23
在一棵树T中最常用的操作是查找某个结点 的祖先结点，采用哪种存储结构最合适？ 双亲存储结构
如最常用的操作是查找某个结点的所有兄弟， 采用哪种存储结构最合适？
孩子链存储结构或者孩子兄弟链存储结构
11/23
2
二叉树
第n个Catalan数
当n=3，结果为5。
12/23
有n个结点并且高度为n的不同形态的二叉树个数是多 少？
A A B
B
T2 T12
…
t11
t2
T11
…
t12
后根序列： B T11 T12 T2 … A
中序序列：B t11 t12 t2 … A
8/23
已知一棵树T的先根序列和后根序列，可以唯一确定这 棵树？

1. 二叉树的定义
二叉树也称为二分树，它是有限的结点集合，这个集合或者是空，或者由 一个根结点和两棵互不相交的称为左子树和右子树的二叉树组成。 二叉树中许多概念与树中的概念相同。 在含n个结点的二叉树中，所有结点的度小于等于2，通常用n0表示叶子结 点个数，n1表示单分支结点个数，n2表示双分支结与度为2的树是不同的。
度为2的树至少有3个结点，而二叉树的结点数可以为0。 度为2的树不区分子树的次序，而二叉树中的每个结点最多有 两个孩子结点，且必须要区分左右子树，即使在结点只有一棵 子树的情况下也要明确指出该子树是左子树还是右子树。
2/35
归纳起来，二叉树的5种形态：
Ø
4/35
3. 满二叉树和完全二叉树
在一棵二叉树中，如果所有分支结点都有左孩子结点和右孩子结点，并且 叶子结点都集中在二叉树的最下一层，这样的二叉树称为满二叉树。
可以对满二叉树的结点进行层序编号，约定编号从树根为1开始，按照层 数从小到大、同一层从左到右的次序进行。
满二叉树也可以从结点个数和树高度之间的关系来定义，即一棵高度为h 且有2h-1个结点的二叉树称为满二叉树。
R={r} r={<ai，aj> | ai，aj∈D， 1≤i，j≤n，当n=0时，称为空二叉树；否则其中
有一个根结点，其他结点构成根结点的互不相交的左、右子树，该 左、右两棵子树也是二叉树 } 基本运算： void CreateBTree(string str)：根据二叉树的括号表示串建立其存储结构。 String toString()：返回由二叉树树转换的括号表示串。 BTNode FindNode(x)：在二叉树中查找值为x的结点。 int Height()：求二叉树的高度。 … }
5
E

7.5 树的应用
➢判定树
在实际应用中，树可用于判定问题的描述和解决。
•设有八枚硬币，分别表示为a，b，c，d，e，f，g，h，其中有一枚且 仅有一枚硬币是伪造的，假硬币的重量与真硬币的重量不同，可能轻， 也可能重。现要求以天平为工具，用最少的比较次数挑选出假硬币， 并同时确定这枚硬币的重量比其它真硬币是轻还是重。
的第i棵子树。 ⑺Delete（t，x，i）在树t中删除结点x的第i棵子树。 ⑻Tranverse（t）是树的遍历操作，即按某种方式访问树t中的每个
结点，且使每个结点只被访问一次。
7.2.2 树的存储结构
顺序存储结构 链式存储结构 不管哪一种存储方式，都要求不但能存储结点本身的数据 信息，还要能够唯一的反映树中各结点之间的逻辑关系。 1.双亲表示法 2.孩子表示法 3.双亲孩子表示法 4.孩子兄弟表示法
21
将二叉树还原为树示意图
A BCD
EF
A
B
C
E
D
F
A
B
C
E
D
F
22
练习：将下图所示二叉树转化为树
1 2
4
5
3
6
2 4
1 53
6
23
7.3.2 森林转换为二叉树
由森林的概念可知，森林是若干棵树的集合，只要将森林中各棵树 的根视为兄弟，森林同样可以用二叉树表示。 森林转换为二叉树的方法如下：
⑴将森林中的每棵树转换成相应的二叉树。 ⑵第一棵二叉树不动，从第二棵二叉树开始，依次把后一棵二叉树 的根结点作为前一棵二叉树根结点的右孩子，当所有二叉树连起来 后，此时所得到的二叉树就是由森林转换得到的二叉树。
相交的集合T1，T2，…，Tm，其中每一个集合Ti（1≤i≤m）本身又是 一棵树。树T1，T2，…，Tm称为这个根结点的子树。 • 可以看出，在树的定义中用了递归概念，即用树来定义树。因此， 树结构的算法类同于二叉树结构的算法，也可以使用递归方法。

需要证明： G不连通， G有两个支， G无圈。
10
2、树的性质
……
u
v
G
（1）如果G是连通的，说明在G中u和v间还 有别的路，加上uv形成圈，这与G是树矛盾，因此 G不连通。
（2）如果G的支多于2个，那么加上边uv， 仍然不连通，这与G是连通的矛盾，因此G的支数 是两个。
（3）因为G中无圈，所以G中无圈。 因此G正好由两棵树构成。
则得到一个有唯一的一个圈的图; (6) G是连通的,并且若p≥3,则G不是Kp,G中任意两个不
邻接的顶点间加一条边,则得到一个有唯一的一个圈的图。
0
证明略。
1
3
2
4
5
自由树（无根树）
7
2、树的性质
定理7.1.1 设G=(V, E)是一个(p, q)图,则下列各命题等价: (1) G是树
(3) G是连通的且p=q+1
第七章：树和割集
7.1 树及其性质 7.2 生成树 7.3 割点、桥和割集
A
B
C
D EF
有根树
0
1
3
2
4
5
自由树（无根树） 1
第七章：树和割集 树（无圈的连通图）、最小生成树、 割点和割集。
内容
树和割集
建模 一般作为极小的连通图、图的骨架 来研究和应用。
2
7.1 树及其性质
本节主要内容 1、树和森林的定义 2、树的性质 3、极小连通图的定义 4、顶点的偏心率 5、图的半径和中心点
(4) G中无圈且p=q+1
0
1
3
2
4
5
自由树（无根树） 8
2、树的性质
(1) G是树

第 7 章 树和二叉树
教材中练习题及参考答案
1. 有一棵树的括号表示为 A(B，C(E，F(G))，D)，回答下面的问题： （1）指出树的根结点。 （2）指出棵树的所有叶子结点。 （3）结点 C 的度是多少？ （4）这棵树的度为多少？ （5）这棵树的高度是多少？ （6）结点 C 的孩子结点是哪些？ （7）结点 C 的双亲结点是谁？ 答：该树对应的树形表示如图 7.2 所示。 （1）这棵树的根结点是 A。 （2）这棵树的叶子结点是 B、E、G、D。 （3）结点 C 的度是 2。 （4）这棵树的度为 3。 （5）这棵树的高度是 4。 （6）结点 C 的孩子结点是 E、F。 （7）结点 C 的双亲结点是 A。
12. 假设二叉树中每个结点值为单个字符，采用二叉链存储结构存储。设计一个算法 计算一棵给定二叉树 b 中的所有单分支结点个数。 解：计算一棵二叉树的所有单分支结点个数的递归模型 f(b)如下：
f(b)=0 若 b=NULL
6 f(b)=f(b->lchild)+f(b->rchild)+1 f(b)=f(b->lchild)+f(b->rchild)
表7.1 二叉树bt的一种存储结构 1 lchild data rchild 0 j 0 2 0 h 0 3 2 f 0 4 3 d 9 5 7 b 4 6 5 a 0 7 8 c 0 8 0 e 0 9 10 g 0 10 1 i 0
答：（1）二叉树bt的树形表示如图7.3所示。
a b c e h j f i d g e h j c f i b d g a
对应的算法如下：
void FindMinNode(BTNode *b,char &min) { if (b->data<min) min=b->data; FindMinNode(b->lchild,min); //在左子树中找最小结点值 FindMinNode(b->rchild,min); //在右子树中找最小结点值 } void MinNode(BTNode *b) //输出最小结点值 { if (b!=NULL) { char min=b->data; FindMinNode(b,min); printf("Min=%c\n",min); } }

max
平均生长量的主要用途 ：
(1)可根据同一生长期平均生长量的大小来比较不同树种在 同一条件下生长的快慢或同一树种在不同条件下生长的快
慢。
(2)材积平均生长量是说明平均每年材积生长数量的指标。 在树木或林分整个生长过程中，平均生长量最高的年轮叫 数量成熟龄，是确定林木采伐年龄的依据之一
三、连年生长量与平均生长量的关系
生长量相等，即Z(t)＝θ(t)时，两条曲线相交。对树木材积来 说，两条曲线相交时的年龄即为数量成熟龄。
(4) 在总平均生长量达到最高峰以后，连年生长量永远小于平
均生长量，即Z(t)＜θ(t) 。
第五节 树木生长率
一、生长率的定义
生长率是树木某调查因子的连年生长量与其总生 长量的百分比，它是说明树木相对生长速度的， 即 Z (t )
• 如上例中的Richards方程：
1 dZ (t ) d 2 y (t ) A c c 1 A 1 2 rc y (t )1 ( ) 1 ( )( )c 2 dt dt y (t ) c y (t )
• 若令
dZ (t ) 0 dt
• 由此可得
V g H f V g H f
• 即： P Pg PH Pf 2PD PH Pf V • 假设在短期间内形 数变化较小(即)，则材积生长率近
D2
用
g
同除上式的两边，得
Pg 2PD
即断面积生长率等于胸径生长率的两倍
三、各调查因子生长率之间的关系（2）
（2）树高生长率(PH)与胸径生长率(PD)的关系 假设树高与胸径的生长率之间关系满足相对生长D(t ) dt
即林木的树高与胸径之间可用如下幂函数表示

七年级地理第七章知识树
七年级地理第七章的知识树主要包括以下内容：
1. 地球的运动：介绍地球自转和公转的原理，解释造成昼夜和季节变化的原因。

2. 气候与气象：介绍气候和气象的概念，了解气候变化的原因和影响因素，认识不同气候带的特点和分布。

3. 气象要素：介绍气温、降水量、风向和风速等气象要素的概念，了解它们的测量方法和对人类生活的影响。

4. 气象图解：学习如何阅读和理解气象图，包括天气图、气温图、降水图等，了解它们的符号和表示方法。

5. 气候变化与人类活动：探讨人类活动对气候变化的影响，包括温室效应、全球变暖和海平面上升等问题。

6. 自然灾害与预防：了解常见的自然灾害，如地震、火山喷发、洪水和飓风等，学习如何预防和减轻其影响。

7. 地理信息系统（GIS）：介绍地理信息系统的概念和应用，了解如何使用地图和卫星图像进行地理研究和分析。

通过学习以上内容，学生可以更好地了解地球的运动规律、气候变化和自然灾害等地理现象，培养对地球环境的关注和保护意识。

伞形或球形。树皮灰褐色，纵裂，内皮层为肉红色。 小枝赤褐色，无 毛。叶互生，三出复叶，小叶椭圆形或椭圆状卵形，缘具钝锯齿，端突 尖或渐尖，基部圆形或近心形，两面光滑，近革质。新发嫩叶淡红色， 秋季老叶褐红色。圆锥花序腋生、下垂，花绿色，雌雄异株。浆果圆形， 成熟时红褐色，种子黑色。花期6～7月，果熟期10～11月 。 [产地与分布]产于我国秦岭、淮河流域以南，至华南北部。长江中下游 一带常见栽培 。
园林树木与花卉
第七章 荫木类园林树木
第七章 荫木类园林植物
主要内容 ①荫木类园林树木概述。 ②28种我国常见应用的荫木类园林树木的 识别要点、产地与分布、习性、繁殖与栽 培、观赏与应用等。

思 考 题
7.1荫木类园林树木概述

7.1.1 荫木类园林植物的特征和特性：荫木类树木即庭 荫树种。庭荫树种的选择标准，因其功能目的所在，主 要为枝繁叶茂、绿荫如盖的落叶树种，其中又以阔叶树 种的应用为佳，如树干通直、高耸雄伟的梧桐，树皮青 绿光滑，树姿高雅出俗，是我国传统的优良庭荫树种。 7.1.2 荫木类园林树木在园林绿化中的作用:主要为置片 片绿荫以避烈日骄阳之淫威，招缕缕爽风以挡酷暑袭人 之热浪，为人们提供一个荫凉、清新的室外休憩场所 。


7.2.3毛白杨

[学名] Populus tomentosa Carr

[科属]杨柳科杨属
7.2.3毛白杨

[识别要点]树冠卵圆形或卵形。树皮幼年时青白色，皮孔菱形；老年时树皮纵裂，呈 现暗灰色。嫩枝灰绿色，密被灰白色绒毛。长枝之叶三角状卵形，先端渐尖，基部心 形或截形，缘具缺刻或锯齿，表面光滑或稍有毛，背面密被白绒毛，后渐脱落；叶柄 扁平，先端常具腺体。短枝之叶三角状卵圆形，缘具波状缺刻，幼年时无毛，后全脱 落；叶柄常无腺体。雌株大枝较为平展，花芽小而稀疏；雄株大枝则多斜生，花芽大 而密集。花期3--4月，叶前开放 。 [产地与分布]主要分布于黄河流域，北至辽宁南部，南达江苏、浙江，西至甘肃东部， 西南至云南均有。垂直分布在200—1200m之间，最高达1800m 。 [习性]强阳性树种，喜温凉气候，在暖热多雨的气候下易受病虫害。对土壤要求不严， 喜深厚肥沃的壤土、砂壤土，不耐过度干旱贫瘠，稍耐碱。耐烟尘，抗污染。深根性， 速生，寿命较长 。 [繁殖与栽培]以无性繁殖为主，多用埋条、留根、压条、分蘖繁殖 . [观赏与应用]该树种树干灰白、端直，树形高大广阔，在园林绿地中很适宜作行道树 及庭荫树。在孤植或丛植于空旷地及草坪上，更能显出其特有的风姿。在广场、干道 两侧规则列植，则气势严整壮观。该树种还是防护林以及用材林的重要树种

第七章园林树木栽植地环境与适地适树以往园林树木的栽植，考虑换土等改造因素较多，对栽植地环境研究认识不够，这样做既不科学又费工费时。

由于科学认识和预见不够，往往达不到应有的功能效果。

植物所生活的空间叫做“环境”，任何物质都不能脱离环境而单独存在，植物的环境主摹包括气候因子(温度、湿度、光照、空气)、土壤因子、水文因子、地形地势因子、生物因子及人类的活动等。

园林树林栽植的环境，广义地说包括自然保护区(相当于欧美的国家公园、游览区内的一切经保护，不加人为改造，只修路和少量进行饮食、住宿服务的设施)、风景名胜区(由自然景观和历史上人为等因素所形成的一类游览资源)、城市园林绿地(基本是由人造或经艺术创造的生活环境)这三大类，其中最典型而有代表性的是城市环境。

园林树木栽植的城市环境是自然和人类生境的综合体，一方面，城市所在地的地理位置、气候、土壤、水文等特征制约着园林树木的树种、品种的选择以及林木生长发育的规律，带有明显的地域性特征；另一方面，城市独特的下垫面性质，决定了城市树木的生长环境与区域大环境在小气候、土壤、水文等方面的不一致性，尤其是人类的生产、生活从时间和空间两个维度深刻地影响、改变着城市树木生长着的环境，并使树木的生长发育深深地打上了人类活动的烙印，就是说树木既要生长在于己不利的有别于自然环境的环境之中，又要使树木的生长发育满足、符合不同时期、不同社会群体的特定需要为目的。

因此，为使园林树木满足其功能和艺术上的需要，研究园林树木栽植地的环境，从城市特定的下垫面性质出发，结合树木自身的生物学、生态学特性，真正做到适地适树，从而使树木能健康长寿的生长，发挥其应有的功能和价值(图7—1)。

第一节城市环境概述一个城市的建成、改建和扩建，对自然环境或生态系统的影响极大。

在原有平原、江河两岸、海滨、湖滨、山谷、山地等地修建城市，包括居住建筑、工厂建筑、道路、广场和其它公共设施的建设，改变了原有的部分地形地貌，各种建筑物、道路等代替了植物的覆盖，即改变了下垫面的性质，进而影响城市的光热状况和土壤状况。

第七章树木生长量测定一、名词解释1.生长量2.早材与晚材3.年轮4.树木的生长方程5.平均生长量与连年生长量6.数量成熟龄7.生长率8.树干解析9.解析木10.定期平均生长量与连年生长量11.总生长量、定期生长量与总平均生长量12.生长曲线13.树木生长理论方程二、填空1.在测树学中，、及是重要的“三大量”。

2.树木生长量的大小及生长速率，一方面受＿的影响，另一方面受的影响。

3.树木生长量按调查因子划分有、、、、和等；按时间划分为、、等；按树木各部分划分有、、等。

4.由于生长率是说明树木生长过程中某一期间的相对速度，所以可以用于及等。

5.在树干解析过程中，应注意截取的圆盘不易过厚，要视树木直径大小的不同而定，一般～cm为宜。

在圆盘的非工作面上要标明，并以分式形式注记，分子为和，分母为＿和。

6.Pv=（k+2）Pd成立的条件是。

7.产生断轮的原因通常是由于。

8.由于树木的生长速度是随树木年龄的增加而变化，即由＿-＿-＿-＿。

9.一个理想的树木生长方程应满足、等条件，且最好能。

10.施耐德材积生长率公式的表达式为。

三、简答1.简述常见的年轮变异现象及其产生的原因。

2.利用年轮法测定树木年龄时应注意哪些问题？3.简述树木生长方程的性质。

4.简述几种常用的树木理论方程。

5.简述平均生长量与连年生长量的关系6.简述三种最常用的生长率公式及其相互间的关系。

7.简述各调查因子生长率之间的关系。

8.简述伐倒木生长量的测定方法。

9.简述立木材积生长量的测定步骤。

10.简述树干解析的外业及工作内容。

11.简述树木生长理论方程与树木生长经验方程的区别。

12.在实践中，为何可以认为普雷斯勒生长率方程是复利式公式的近似式？13.简述Richards生长方程的生物学假设。

14.简述逻辑斯蒂方程的性质。

15.简述伪年轮的一般特征。

16.简述平均生长量的主要用途。

四、计算1.已知一株红松，60年生时的材积为0.2746m3,70年生时为0.3921 m3，计算其70年生时的总生长量、总平均生长量，以及60－70年间的定期生长量、定期平均生长量、连年生长量。

数据结构作业第7 章1.假设每个结点值为单个字符，而一棵树的层次遍历序列为ABCDEFGHIJ，则其根结点的值是。

A．A B. B C. J D. 以上都不对2.在一颗3 次树中度为3 的结点数为两个，度为2 的结点数为一个，度为1 的结点数为两个，则度为0 的结点数为个。

A．4 B. 5 C. 6 D. 73 . 对于一棵具有n 个结点、度为4 的树来说，。

A.树的高度最多是n-3B. 树的高度最多是n-3C. 第i 层上最多有4(i-1)个结点D. 至少在某一层上正好有4 个结点4.在任何一棵二叉树中，如果结点a 有左孩子b、右孩子c、则在结点的先序序列、中序序列、后序序列中，。

A.结点b 一定在结点a 前面B. 结点a 一定在结点c 前面C. 结点b 一定在结点c 前面D. 结点a 一定在结点b 前面5.设a、b 为一颗二叉树上的两个结点，在中序序列时，a 在b 之前的条件是。

A．a 在b 的右方 B. a 是b 的祖先C. a 在b 的左方D. a 是b 的子孙6.若二叉树的中序序列是abcdef，且c 为根结点，则。

A.结点c 有两个孩子B. 二叉树有两个度为0 的结点C. 二叉树的高度为5D. 以上都不对7.设有13 个值，用他们组成一颗哈夫曼树，则该哈夫曼树共有个结点。

A．13 B. 12 C.26 D. 258.在n 个结点的线索二叉树中（不计头结点），线索的数目为。

A.n-1B. nC. n+1D. 2n9.一棵度为2 的树中，其结点个数最少为。

10.设某棵树中结点值为单个字符，其后根遍历序列为ABCDEFG，则根结点值为。

11.一共8 层的完全二叉树至少有个结点，具有100 个结点的完全二叉树中结点的最大层数为。

12.设一棵完全二叉树（每个结点值为单个字符）的先序序列为abdecf，则该二叉树的中序序列为、层次序列为。

13.一棵二叉树的先序、中序和后序序列分别如下，其中有一部分未显示出来。

TBTNode *CreaThread(TBTNode *b) //线索化二叉树
算法设计
0 A 0
0
0
1
B
0
1 C
1 E 1
1
1
D
1
增加一个头结点，将整棵树作为他的左孩子 选择一种遍历方式，将二叉树线索化，生成某种 访问顺序的线索化二叉树。
TBTNode *CreaThread(TBTNode *b) /*中序线索化二叉树*/ { TBTNode *root; root=(TBTNode *)malloc(sizeof(TBTNode)); /*创建头结点*/ root->ltag=0;root->rtag=1; root->lchild=b; { 0 1 pre=root; pre Thread(b); 0 A 0 pre->lchild=root; pre->rtag=1; 0 B 0 1 C 1 root->rchild=pre; } 1 D 1 1 E 1 return root; }
3
6 7
结点1到5之间的路径长度：2 树的路径长度：1+1+2+2+2+2+2=10
• 树的带权路径长度WPL：设树中有M个叶结点， 每个叶结点带一个权值WK，树根到每一个叶结点 K的路径长度为LK则WPL =。m
w
k 1
k
lk
哈夫曼树：WPL最小的树称为最优二叉树，又称哈夫曼树
举例：有4个叶结点a,b,c,d权值分别为7，5，4，2， 请构造出哈夫曼树
哈夫曼树的构造过程
7 a 5 b (a) 7 a 11 a c (c) d (d) b c d 2 c 4 d 7 a (b) 5 b c 6

18
7.2 生成树
使得(T0-e1)+e2为生成树, 设(T0由e假1)设+知e2d=(TT10,,T)=n+1,
d(T1,T)=n, 由归纳假设,从T1经n个基本树变换便到T, 因此从T0经n+1个基本树变换得到
T 因此定理成立。
19
7.2 生成树
最小生成树问题 生成树的权
3
3
2 1 1
(1)G是树
(2)G的任意两个不同顶点间有唯一的一条路联结;
(3)G是连通的且 p(4=)Gq+中1无; 圈且 (p5=)Gq+中1无; 圈且G中任意两个不邻接的顶点间加一 条边,则得到一个有唯一的一个圈的图;
(6)G是连通的,并且若p≥3,则G不是Kp,G中任意 两个不邻接的顶点间加一条边,则得到一个有唯一的一 个圈的图。
24
7.2 生成树

4
4
v 3 3
e 1
2
图u G

4
4
v 3 3
e 1
2
u生成树T
生成树T的权是包含生成森林的生成树中权 最小的生成树。
25
7.2 生成树
[证]用反证法证明 如若不然,则G有一个生成树T=(V,E),T包含 F(即FE),不包含边e；
11
7.2 生成树
定理7.2.2 具有p个顶点的完全图Kp有pp-2棵 生成树,p≥2.
设一棵树的顶点集为A
1
2
3
5
1、从中找到编号最小的叶 子结点，去掉该叶子结点a1 4 及其邻接边(a1,b1)。
2、重复以上过程。只到剩 一条边为止。
(1,2),(4,3),(3,2)