当前位置：文档之家 › chapter5-3+Nyquist稳定性判据及稳定裕度1[1]

chapter5-3+Nyquist稳定性判据及稳定裕度1[1]

  • 格式：ppt
  • 大小：2.78 MB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

乃奎斯特稳定判据对数稳定判据和稳定裕度

乃奎斯特稳定判据对数稳定判据和稳定裕度

则不存在闭环极点，因而系统是稳定的。
7
Im 1 GH 平面
Re 01
1 G ( j )H ( j )
j s 平面
0
Im GH 平面
图5-37 s平面内的封闭曲线
1 1 G( j)H ( j)
Re 0 G( j )H ( j )
1H(j)G(j)
曲线对原点的包围，恰等于
H(j)G(j) 轨迹对-1+j0点的包围
4
5.5.2影射定理 设 F (s) 为两个s的多项式之比，并设P为 F (s) 的极点数，Z为
F (s) 的零点数，它们位于s平面上的某一封闭曲线内， 且有多重极点和多重零点的情况。设上述封闭曲线不通过
F (s) 的任何极点和零点。于是，s平面上的这一封闭曲线影射到 F (s) 平面上，也是一条封闭曲线。当变量s顺时针通过封闭曲线时 在 F (s) 平面上，相应的轨迹顺时针包围F (s) 原点的总次数R等于Z-P。
H(s)G(s)
1 在右半s平面内有一个极点 s 1
4K
P1 因此开环系统是不稳定的
GH 平面
1 K
Re
2 图5-45表明 H(s)G(s)
轨迹逆时针方向包围-1+j0一次
0
R1
3 ZRP0
图5-45 H(j)G(j)极坐标图 没有零点位于右半s平面内，闭环系统是
说明 1H(s)G(s) 稳定的。这是一个开环系统不稳定，但是 回路闭合后，变成稳定系统的例子。 27
如果函数 H(s)G(s) 在右半s平面内无任何极点，则
因此，为了保证系统稳定， G(j)H(j)
的轨迹必须不包围-1+j0点。
ZR
9
5.5.6 G(s)H(s) 含有位于 j 上极点和/或零点的特殊情况
系统稳定性

系统稳定性


第五章 系统的稳定性
例： 已知单位反馈系统开环传递函数 2 = GK s s- 1 试判别系统闭环后的稳定性 解：由GK(s)得，开环系统有 一正极点 ∴开环系统不稳定 P=1 GK(j)的N氏图如右。
GK(j)正向包围(-1,jo)点半圈 N = 1= P
=o (-1,jo)
Im
o =
L
第五章 系统的稳定性
D1=an-1>0
an-1 D2 = an an-3 >0 an-2
Dn>0
an-1 an-3 an-5 D3 = an-2 an-4 an-6 >0 0 an-1 an-3
Hurwitz行列式直接由系数排列，规律简单 而明确，因此，比列Routh表要简单些，使用也 较为方便，但对六阶以上的系统，由于行列式 计算麻烦，故应用较少。对于简单形式：
n = 2 : a2 > 0 n = 3 : a3 > 0 n = 4 : a4 > 0 a1 > 0 a2 > 0 a3 > 0 a0 > 0 a1 > 0 a2 > 0 a0 > 0 a1 > 0 a 2 a1 - a 0 a 3 > 0 a0 > 0
2 >0 a1 a 2 a 3 - a12 a 4 - a 0 a 3

1 ×3 - 1 ×5 = -2 1
2 + 2

5 0 0
-2 5
∵ 第一列符号改变两次
∴系统不稳定，有两个具有正实部的特征根。
第五章 系统的稳定性 2）Routh表某行元素全为零：（若第k行）
处理方法： a)以上一行（k-1）行的系数构成一个辅助方程 （阶次一般为偶数）Sn-k+2
控制工程基础 (第12讲) 第五章 乃魁斯特(Nyquist)稳定性判据 PPT课件

控制工程基础 (第12讲) 第五章 乃魁斯特(Nyquist)稳定性判据 PPT课件


如果在s平面上曲线包围k个零点和k个极点(k=0,1,2…)，
即包围的零点数与极点数相同，则在 F(s) 平面上，
相应的封闭曲线不包围 F(s) 平面上的原点。
上述讨论是映射定理的图解说明，奈奎斯特稳 定判据正是建立在映射定理的基础上。
相角（幅角）定理：
如果闭合曲线 s 以顺时针方向为正方向，在 s 平
在右半s平面内的零点数和极点数联系起来的判据。这 种方法无须求出闭环极点，得到广泛应用。
奈奎斯特稳定判据是建立在复变函数理论中的图形映 射基础上的 。
相角（幅角）定理：
如果闭合曲线 S 以顺时针方向为正方向，在[S]平
面上包围了Fs 的 Z 个零点和 P 个极点，但不经过
任何一个零点和极点，那么，对应的映射曲线 F 也以
奈魁斯特稳定判据是利用开环频率特性判别闭环系统的稳 定性。不仅能判断系统的绝对稳定性，而且可根据相对稳定的 概念，讨论闭环系统的瞬态性能，指出改善系统性能的途径。 它从代数判据脱颖而出，故可以说是一种几何判据。
06-7-20
控制系统系统的稳定性分析
2
奈魁斯特稳定判据无需求取闭环系统的特征根，而是利用
F(s) 的轨迹将逆时针方向包围 F(s)平面上原点两次
06-7-20
控制系统系统的稳定性分析
9
s平面
B3

2
1
A0
-1

-2
F -3 -3

-2
-1
j
Im
C
2
1.5
F (s)平面
1 B1
0.5
D
E1
0 C1
F1 -0.5
-1
A
-1.5
D1
5-3 Nyquist稳定判据

5-3 Nyquist稳定判据


由于G(s)H(s)曲线的对称性，因此可以用系统的开环频率 特性曲线G(j)H(j)对(-1,j0)的包围情况来判断。
设特性曲线G(j)H(j)对(-1,j0)的逆时针包围次数为N 则R=2N（注意补充积分环节Nyquist围线上小1/4圆的象） 也可用G(j)H(j)曲线对(-∞, -1)实轴段的穿越计算N
3
5.3.1 预备知识
1. 幅角原理
s：复变量; F(s)：复变量s的有理函数
对于s平面上一条不通过F(s)任何奇点的连续封闭曲 线Γ，在F(s)平面必存在一条封闭曲线ΓF与之对应j
F
F(s)平面
F (s )
F

映射关系
4
( s z1 )( s z2 ) 设 F ( s) ( s p1 )( s p2 )
终点

A() 0
() 270
20
与实轴交点
52(10 4 2 ) j52 (9 2 ) G( j ) (4 2 ) (5 2 ) 2 4 2


(9 2 ) 0 0, 3
52(10 4 2 ) G(3 j ) (4 2 ) (5 2 ) 2 4 2
5
Im[F(s)] [F(s)]
F
F(s)
s沿Γ顺时针运动一周时
(s z1 ) (s p1 ) 2
(s z2 ) (s p2 ) 0
即ΓF不包围F(s)平面上的原点
F ( s) 0
6
幅角原理：设s平面闭合曲线Γ包围F(s)的Z个零点和 P个极点，当s沿Γ顺时针运动一周时，在F(s)平面 上，对应的闭合曲线ΓF逆时针包围原点的圈数
§5-3 奈魁斯特稳定判据

§5-3 奈魁斯特稳定判据


§5-3 奈魁斯特稳定判据
反馈控制系统稳定的开环频率 特性曲线逆时针包围（-1，0j） P:开环右极点个数 点的圈数与系统的开环右极点 的个数P相等，则闭环系统稳定。 R:包围（-1，0j）点的圈数
Z PR
(a) R=0
(b)R=0
(c) R=0
(d)R=-1
(e)R=-3
ቤተ መጻሕፍቲ ባይዱ
例题5-2
已知单位反馈系统开环幅相曲线 （K=10,P=0,ѵ=1）如右图所示，试确定闭环稳 定时K值的范围. 解 由图可知，开环幅相曲线与负实轴有三个交点， 1 , 2 , 3 设交点处频率分别为
取K 10时，G ( j1 ) 2,
若令G ( ji ) 1, 可得对应的K值
0 K K1 , R 0, Z 0,闭环系统稳定； K1 K K 2 , R 2, Z 2,闭环系统不稳定； K 2 K K 3 , R 0, Z 0,闭环系统稳定； K K 3 , R 2, Z 2,闭环系统不稳定。 综上，系统闭环稳定时 值范围为（ ， K 0 5）和（ 20 ， ). 20 3
K G1 ( S ) S 由题设条件知 1， G1 ( S ) 1 lim G(S )
s 0
G ( j i )
K G1 ( ji ) j i
i 1,2,3 G ( j 2 ) 1.5, K1 1 j1 G ( j3 ) 0.5 1 G1 ( j1 ) 5, K 2 20 , K 3 20 3
(第13讲) 第五章 乃魁斯特(Nyquist)稳定性判据

(第13讲) 第五章 乃魁斯特(Nyquist)稳定性判据


在控制系统应用中，由
F (s) 1 G (s)H (s)
很容易确定
的P数。因此，如果， F (s )
的轨迹图中确定了R，则s平面上封闭曲线内的零点数
很容易确定。
开环传递函数与闭环传递函数的关系：
06-7-20
控制系统系统的稳定性分析
14
R(s)
C(s) G (s )
G (s)
B1 ( s ) A1 ( s )
06-7-20
控制系统系统的稳定性分析
3
奈奎斯特稳定判据(Nyquist Stability Criterion) 闭环传递函数
C (s) R (s) G (s)
R(s) G (s )
C(s)
H(s )
1 H ( s )G ( s )
图5-4-1 闭环系统 结构图
1 H ( s )G ( s ) 0
例如：考虑下列开环传递函数：
06-7-20 控制系统系统的稳定性分析 6
G (s)H (s)
6 ( s 1)( s 2 )
其特征方程为：
6
F (s) 1 G (s)H (s) 1
( s 1)( s 2 )

( s 1 . 5 j 2 . 4 )( s 1 . 5 j 2 . 4 ) ( s 1)( s 2 )
控制系统系统的稳定性分析 11
如果在s平面上曲线包围k个零点和k个极点(k=0,1,2…)，
即包围的零点数与极点数相同，则在 F ( s ) 平面上，
相应的封闭曲线不包围
F (s)
平面上的原点。
上述讨论是映射定理的图解说明，奈奎斯特稳 定判据正是建立在映射定理的基础上。
第五章 系统的稳定性

第五章 系统的稳定性

1 GK (s) =G( s)H ( s ) = M ( s ) ( n> m ) N(s ) 2. GB ( s ) = G( (s s) 1 + G (s)H (s)
H(s) Xi(s) G( ) G(s)
3）系统稳定的充要条件是GB(s)的全部极点在s平 面的左半部⇒F(s) ( )的全部零点在s平面的左半面。
a n− 1 an 0 0 a n− 3 a n− 2 a n −1 an a n−5 a n− 4 a n− 3 a n− 2
Δ1=an-1>0 Δ2 = Δn>0
an-1 an an-3 >0 an-2
Δ3 = an-2 an-4 an-6 >0
0 an-1 an-3
an-1 an-3
an-5
L L L L M
或s3+3s=0
0 0
8
∵ 第一列元素符号没有变化 ∴ 系统稳定
第五章 系统的稳定性
第五章 系统的稳定性
二、Hurwitz( 二、 Hurwitz(赫尔维兹 赫尔维兹) )判据
D(s)=ansn +an-1sn-1 +…+a0=0 系统稳定的充要条件： 1）特征方程各项系数均大于零 2）Hurwitz行列式Δk>0 (k=1,2,…,n)
2 >0 a1 a 2 a3 − a12 a 4 − a 0 a 3
M
0 0
M L
M L
a2
E X E
第五章 系统的稳定性
第五章 系统的稳定性
§5-3
Nyquist稳定判据
由此可见： 1）F(s)的极点就是GK(s)的极点 2）F(s)的零点就是GB(s)的极点
Xo ( (s) )
机械工程控制基础(第五版) 第五章系统的稳定性课件

机械工程控制基础(第五版) 第五章系统的稳定性课件


本章难点
Nyquist判据及其应用。
5.1 系统稳定性的初步概念
5.2 Routh稳定判据
n Routh判据：通过系统特征方程的各项 系数进行代数运算，得出全部根具有 负实部的条件。从而判别系统的稳定 性，是一种时域判据。
一、系统稳定的必要条件
二、系统稳定的充要条件
三、Routh判据特殊情况
n 例5:设系统特征方程为
D(s)=s5+2s4+24s3+48s2-25s-50=0
试用Routh判据判别系统的稳定性.
解:列Routh表:
S5
1
24
-25
S4
2
48
-50
S3
0
0
0
由第二行各元构造辅助方程:
幂次)
2s4+48s2-50=0
(注意s的
取F(s)对s的导数:8s3+96s=0
S3中各元可用此方程中系数8和96代替,得Routh 表如下:
5.4 Bode稳定判据
n 一、Nyquist图和Bode图的对应关系 n 二、穿越的概念 n 三、Bode判据
一、Nyquist图和Bode图的对应关系
二、穿越的概念
三、Bode判据
5.5 系统的相对稳定性
The End！
比较这三个式子：
GB(s) GK(s)
F(s)
零点 零点
极点 极点ຫໍສະໝຸດ 零点极点n 3、幅角原理（映射定理）
二、Nyquist稳定判据
n 1、s平面封闭曲线的选择
n （3）平面[s]上，将-j∞→＋j∞→∞组成的曲线， 换成仅由虚轴（即-j∞→j∞）代表的曲线。
n 综上所述，Nyquist判据表述如下：
机械控制工程5章-3

机械控制工程5章-3


(s p )
j j 1
① F(s)分母与GK(s)分母相同，故F(s)的极点pj即为GK(s)的极点；
② F(s)分子与GB(s)分母相同，故F(s)的零点zi即为GB(s)的极点；
③ 各函数零点、极点对应关系如图示：
GB ( s )
极点
G 1 GH
F ( s) 1 GH
零点 极点
[s]
Im
s
jv
[F(s)]
F(s)=u+jv u LF
z3
LS
二、幅角原理
(1) 设F(s)在[s]平面上(除有限个奇点外)为单值的连续正则函数； (2) 设在[s]平面上解析点s映射[F(s)]平面上为点F(s)，或为从原点指向该映 射点的向量F(s) ； 点A (s=σ+jω) → →点B (F(s)=u+jv)
Ls可以认为包围了整个[s]平面的右半平面。当ω从-∞→+∞时， 轨迹的方向为顺时针。
2、[F]平面的Nyquist轨迹－－LF
[F]平面的Nyquist轨迹按函数F(s)(=1+GH=u+jv)作出，若其图形不包 围原点，即N=0，说明相应的Ls 曲线所包围的F(s)的零、极点数相等，即 Z=P。 结论：系统稳定的充要条件是Z=0。 为保证Z=0，即N=Z-P =-P。 也就是当[F]平面的Nyquist轨迹LF逆时针包围 原点的圏数N，等于F(s)函数位于[s]平面的右半平 面的极点数P时，则系统稳定。
§5-3 Nyquist稳定判据 通过GK(jω)的Nyquist图，利用图解法来判断闭环系统 的稳定性－－几何判据
优点：
① 是图解法，避免了求解特征方程的繁琐过程； ② 某些环节的传递函数无法用分析法列写时，可通过实验获得其频率 特性曲线，以分析其稳定； ③ Nyquist稳定判据还能指出系统的稳定性储备－－相对稳定性。 以及进一步提高和改善系统动态性能（包括稳定性）的途径； ④ 若系统不稳定，则Nyquist判据还能如Routh判据那样，指出系统不稳 定的闭环极点个数，即具有正实部的特征根的个数。
第五章系统的稳定性1

第五章系统的稳定性1

i =1 j =1 m n
假定在 s 平面上的封闭曲线 Γs 包围了 F(s) 的一个零点 z1，而其他零极点都位于封闭曲线之外； 当 s 沿着 s 平面上的封闭曲线 Γs 顺时针方向移动一周 时，向量(s－z1)的相角变化－2π 弧度，而其他各相量 的相角变化为零； 这意味着在 F(s) 平面上的映射曲线 ΓF 沿顺时针方向围 绕着原点旋转一周，也就是向量 F(s) 的相角变化了－ 2π 弧度。
20
5.3 Nyquist稳定判剧
一、映射定理（幅角定理） 二、Nyquist稳定性判据 三、虚轴上有开环极点的Nyquist稳定判据
21
5.3
Nyquist(乃奎斯特)稳定判据
¾Routh判据是根据系统特征方程的根在复平面内的 分布情况来判稳的，是代数判据，时域判据； 几何判据（频域稳定判据）：Nyquist稳定判据 （简称乃氏判据）和对数频率稳定判据。
也称代数判据，基于特征方程根与系数的关系而 建立。利用该判据，可以在不解方程在情况下， 可以判定一个多项式方程中是否存在位于复平面 右半部的正根，从而判断系统的稳定性。 一、系统稳定的必要条件
n n−1 D ( s ) = a s + a s + ⋅ ⋅ ⋅a1s + a0 = 0 设系统特征方程为： n n−1
二、系统稳定的充要条件 1、劳斯表的编制
将系统特征多项式系数按下面的方式编制劳斯表：
sn s n −1 s n−2 s .. .. s
n −3
an
an −2
an −4 .. an −5 ..
an−1 an −3
前两项为多项式系 数，从第三行开始：
an an − 2 an −1 an −3 b1 = − an −1
Nyquist稳定性判定

Nyquist稳定性判定

开环Nyquist曲线在(-1,j0)点以左穿过负实轴 ➢负穿越——相位角减小的穿越 ➢正穿越——相位角增大的穿越 ➢半次穿越—开环Nyquist曲线从(-1,j0)点以左的负实轴开始的穿越
正负穿越次数的代数和即为N
第五章 系统的稳定性
5.3 Nyquist稳定判据
三、开环含有积分环节时的Nyquist稳定判据 存在的问题：
第五章 系统的稳定性
例5.6
Im
P=0
ω=+∞ K 1
-1 0
ω=0
Re
5.3 Nyquist稳定判据
Im
P=0
-1
ω=+∞
0
K2 ω=0
Re
(a)
N=0，P=0 → P=2N 稳定
(b)
N=-1，P=0 → P≠2N 不稳定
开环增益K的增大不利于系统的稳定性。
第五章 系统的稳定性
例5.7
P=1 Im
第五章 系统的稳定性
5.3 Nyquist稳定判据
一、Nyquist稳定判据
P:169 当ω从-∞→＋∞变化时，GK(jω)的Nyquist曲线逆时针方向 包围(-1,j0)点P圈，则闭环系统稳定。其中，P为开环右 极点的个数。
注意：
GK(jω)的Nyquist曲线当ω从-∞→0变化时与其从0→ +∞变化
开环Nyquist曲线不封闭，无法准确判断其包围(-1,j0)点的圈数
解决的办法：
作辅助曲线
以无穷大为半径，从Nyquist曲线的起始端沿逆时针方向绕 过ν×90°作圆弧和实轴相交，这个圆弧就是辅助曲线。
ν——开环传递函数中含有积分环节的个数
第五章 系统的稳定性
例5.9 P=0 Im

奈奎斯特稳定性判据-精华篇


小结
1. 奈奎斯特判据是根据开环奈奎斯特图判断闭环 系统的稳定性；
2. 奈奎斯特稳定判据的内容：若系统稳定，则系 统的开环频率特性按逆时针方向包围（-1，j0） 点的圈数为N圈，等于位于S右半平面的极点数P。
作业
课后作业题： P86-7.3，7.4，7.5。
例题：根据奈氏轨迹判断系统稳定性
1
P0
0
∵ N=-2
P0 N P
0

∴ 系统不稳定。
奈氏判据判定步骤
1. 根据G(s)H(s)画奈氏曲线； 2. 以实轴为镜像，画从0-→-∞的奈氏轨迹； 3. 若有 个积分环节，则应由 0 起到 0 终给奈氏轨迹增补 R ，顺时针转 的大圆弧； 4. 计算奈氏轨迹绕（-1，j0）点转的圈数N。 5. 求得开环右半平面极点数P； 6. 若N=P，则系统稳定，否则系统不稳定。
s j
b. 有s=0时，[GH]为 R
k ( s z1 )( s z 2 ) ( s z m ) G( s) H ( s) v s ( s p1 )( s p 2 ) ( s p n v )
S=0
G s H s
即： 个积分环节 [GH]上从 0 到 0 以 R 转 圆弧。
一系统稳定性的定义和条件二nyquist奈奎斯特稳定判据的推导三结论与举例四小结一系统稳定性的定义和条件不稳定系统所谓稳定性就是指扰动消失后系统由初始状态恢复到原来平衡状态的性能
奈奎斯特稳定性判据
主要内容
一、系统稳定性的定义和条件 二、Nyquist（奈奎斯特）稳定判据的推导 三、结论与举例 四、小结
若
则
GK s G s H s

53-54奈氏判据和稳定裕度

– Nyquist判据根据开环幅相曲线判别闭环系统稳定性； – 对数频率稳定判据根据开环对数频率特性曲线判断闭环系 统稳定性；
– 两种频率稳定判据没有本质区别。
• 频域稳定判据的特点：根据开环系统频率特性曲线判 定闭环系统的稳定性，并能确定系统的相对稳定性。
• Nyquist稳定判据的优点
– 图解法、几何判据，简单、直观、计算量小（ 劳斯/赫尔维茨判据是代数判据）。
jV F(s) 平面 jV G(s)H(s) 平面
(-1, j 0)
0 CF
U
(-1, j 0)
0
U
CGH
乃氏曲线映射在F(s) 平面和G(s)H(s) 平面上
绘制映射曲线CGH 的方法是： • 对应于C1的映射曲线：令 s＝jω代入G(s)H(s)，得到 开环频率特性 G(jω)H(jω)，画出乃氏图，再画出其 对称于实轴的、ω 从0变到－∞的那部分曲线。
3. 映射定理
• 映射定理：设s平面上的封闭曲线Γs包围了复变函数 F(s)的P个极点和Z个零点，并且此曲线不经过F(s)的 任一零点和极点，则当复变量 s沿封闭曲线Γs顺时针 方向移动一周时，在F(s)平面上的映射曲线ΓF按逆时 针方向包围坐标原点P－Z周。 • 可见， F平面上曲线绕原点的周数和方向与 s平面上 封闭曲线包围F(s)的零极点数目有关。
②
我们感兴趣的不是映射曲线ΓF的形状，而是它包 围坐标原点的次数和运动方向，因为这两者与系 统的稳定性密切相关（都与F(s) 的相角变化有关 系）。
2.复变函数F(s)的相角表示及其变化
F ( s)
K ( s z1 )( s z2 )( s zm ) ( s p1 )( s p2 )( s pn ) 复变函数F(s)的相角可表示为

chapter5-3+Nyquist稳定性判据及稳定裕度1[1]

s为复变量，以s复平面上的s=δ+jω来表示。F(s)为复变函数， 以F (s)复平面上的F (s)= u+j v表示。点映射关系，如图1所示。 s平面与F(s)平面的曲线映射关系，如图2所示。
图1
点映射关系
图2 s平面与F(s)平面的映射关系
如果在s平面上任取一条封闭曲线Cs， 且要求Cs曲线满足：曲线Cs包围F(s) 的Z个零点和P个极点。s平面上的封 闭曲线Cs如图3所示。
Im
1 GH平面
2


2
， R 得第二部分的映射；令 从 0 ，
Im
GH平面
Re 01 1 G( j)H ( j)
1
1 G( j)H( j)

0
Re
G( j)H ( j)
Im
1 GH平面
Im
GH平面
01 1 G( j)H ( j)
Re
1
1 G( j)H( j)
度由

得第三部分的映射。 得到映射曲线后，就可由柯西幅角定理计算 R P Z ，式中： P, Z 是F(s)在s右半平面的零点数和极点数。确定了R，可求出 Z P R 。当 Z 0 时,系统稳定；否则不稳定。
第2个问题：辅助方程与开环频率特性的关系。我们所构造的辅 助方程为 F (s) 1 G(s)H s 因此，有以下结论是明显的：
结论： (s z1 ) 2 (s zk ) 0 (k 2,3)
(s p j ) 0 ( j 1, 2,3)
F (s) [(s z1 ) (s z2 ) (s z3 )] [(s p1 ) (s p2 ) (s p3 )]
顺时针围绕 (-1,j0)点的圈

第五章Nyquist稳定判据


a G( j a ) H ( j a ) 1
G( j a ) H ( j a ) 1, G( j a ) H ( j a ) 180 0
可求解出一对虚根 j a 。
此时，系统输出和输入的幅值比为1，相位差为-180°。
例5-6
开环传递函数如下： GH

• • •
5.2.1 奈魁斯特稳定判据
利用开环频率特性G(jω)H(jω)判别系统闭环稳定性。
（ 1 ）当系统为开环稳定时，只有当开环频率特性 G(jω)H(jω)不包围（-1，j0）点，闭环系统才是稳定 的。 （ 2 ）当开环系统不稳定时，若有 P 个开环极点在 [s] 右半平面时，只有当G(jω)H(jω)逆时针包围 1，j0）点P次，闭环系统才是稳定的。 （-
s 0 : G( j j ) j ( A'点),

s 0 : G( j j ) j ( B'点）
A
D × C
GH
K G( s) H ( s) s(Ts 1)
B
G( e ) H ( e )
j
j
0

K
e (T e 1) 0
在正频范围内计算ω>0：
确定起始点：ω=0时， 终点：ω→∞
G( j K 0.1K
分析 ：
G j ) 0
当 3时， 虚部为零。 3时， 虚部为负， 3时， 虚部为正。 K 把 3代入实部， 求出Re [G( j 2 3 28
奈魁斯特稳定判据总结

利用开环频率特性判断闭环系统的 稳定性 F(s)=1+G(s)H(s)
闭环特征多项式

nyquist稳定判据定义

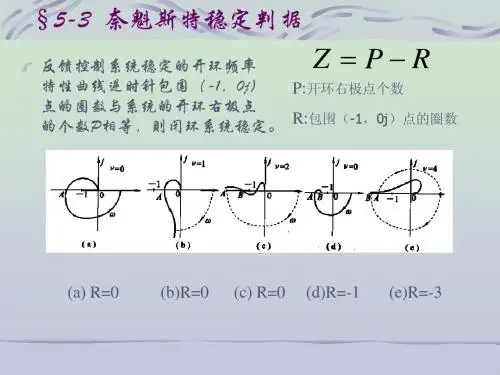
nyquist稳定判据定义
Nyquist稳定判据是一种用于确定系统稳定性的方法，它基于系统的频率响应特性。

在Nyquist稳定判据中，通过将系统的传递函数表示为极坐标形式，然后绘制系统的Nyquist曲线，可以判断系统是否稳定。

具体地说，如果系统的Nyquist曲线的完整轨迹都位于单位圆内部，则系统是稳定的。

如果曲线穿过单位圆，但是穿过的次数等于系统开环传递函数的极点数减去零点数，则系统是边缘稳定的。

如果曲线穿过单位圆的次数超过系统开环传递函数的极点数减去零点数，则系统是不稳定的。

Nyquist稳定判据在控制系统设计和分析中有着广泛的应用，特别是在反馈控制系统中。

它不仅可以用于稳定性分析，还可以用于确定系统的相位余量和增益裕度等重要指标。

因此，掌握Nyquist稳定判据的定义和应用是控制工程师必备的基本技能之一。

- 1 -。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

s
p1
A
z1
j Im
s z1
z3
p2
0
p3

F
s z2
F ( s) B F (s) 0
Re
z2
在F(s)平面上，F(s)是对应于从B点出发又回到B的围线 F 。
设 (s z i ) , 分别是向量 沿着围线顺时针绕行一 (s z i ) , (s p j ) (s p j ) 周的相角变化量。考察s沿着围线F(s)的相位变化量为：
(s p k ) 0 (k 1,2, n, k j )
F
(s z i ) 0 (i 1,2, n)
F (s) 2
F ( s) B F ( s) 0
Re
[柯西幅角定理]：s平面上不通过F(s)任何奇异点(s平面上F(s)的
Z个零点和P个极点)的封闭曲线 。当 s s以顺时针方向沿封闭曲 方向绕坐标原点旋转R圈。R，Z，P的关系为：R= P-Z。 若R为正，表示 f 逆时针运动，且包围原点R圈；
难点：相对稳定性
要求：熟练运用奈奎斯特判据判据确定系统的稳定性；明理
稳定裕度的概念，熟练用解析法和图解法计算稳定裕度
3
幅值裕度 相角裕度
重点：奈奎斯特稳定判据、对数频率稳定判据及稳定裕度
一、映射定理(幅角定理)
F(s)是复变量s的单值有理函数。如果函数F(s)在s平面上指定 的区域内是解析的，则对于此区域内的任何一点s0都可以在F(s) 平面上找到一个相应的点F(s0), 称为F(s0)在F(s)平面上的映射。
Automatic Control Theory
河南理工大学电气工程与自动化学院
Henan Polytechnic University (HPU)
School of Electrical Engineering and Automation
课程名称：自动控制原理
主讲教师：乔美英
河南理工大学自动控制原理
F ( s)
K ( s z i )
i 1mΒιβλιοθήκη (s p )j 1 j
n
图3 映射关系
当试验点 s1（封闭曲线Cs上任一点 ）沿闭合曲线Cs顺时针转
动一圈时，复变函数F(s)，其矢量总的相角增量为（净相角）
矢量总的相角增量为（净相角）：
F ( s ) ( s zi ) ( s p j )
j
s
p1
A
z1
j Im
s z1
z3
p2
0
p3

F
s z2
F ( s) B F (s) 0
Re
z2
F (s) [(s z1 ) (s z2 ) (s z3 )] [(s p1 ) (s p2 ) (s p3 )]
G ( j )
K G ( s) (T1 s 1)(T2 s 1)
K K 2 2 2 1 T T j (T1 T2 ) 1 2 2 2 ( jT1 1)( jT2 1) (T1 1)(T2 1)
j Im


（2）用奈氏判据判定闭环 系统的稳定性
P0 R0
Z 0
K Re 1 0 0
系统是闭环稳定的。
52 Gk ( s) [例2]设开环系统传递函数为： ，试用 ( s 1)(s 2 2s 5)
奈氏判据判断闭环系统的稳定性。 [解]：开环极点为-1，-1 j2，都在s左半平面，所 以 P 0 。奈氏图如右。 从图中可以看出：奈氏图
F (s) 2
这表明: F 曲线从B开始，绕原点顺 时针方向转了一圈。若在s平面的顺 时针围线内，包围的是某个极点pj， 在F(s)平面上， F 曲线绕原点逆时针 方向转了一圈。即
p1
j
s
A
0
z1
s z1
z3
p2
p3

s z2
z2
j Im
(s p j ) 2
N (s) M (s) N (s)
其零点恰好是闭环系统的极点，因此，只要搞清F(s)的的零点
在s右半平面的个数，就可以给出稳定性结论。如果F(s)的右
半零点个数为零，则闭环系统是稳定的。 如果有一个s平面的封闭曲线能包围整个s右半平面，则根据柯 西幅角定理知：该封闭曲线在F(s)平面上的映射包围原点的次
作出ω=0→+∞变化时G(jω)H(jω) 曲线如图5所示，镜像对称得ω： -∞→0变化时G(jω)H(jω) 如图5 虚线所示。 系统开环不稳定，有一个位于s
平面的右极点，即P=1。
图5 系统的极坐标图
从G(jω)H(jω)曲线看出，当K>1时，Nyquist曲线逆时针包 围(-1，j0)点一圈，即N=1，Z=N-P=0则闭环系统是稳定的。 当 K<1 时， Nyquist 曲线不包围 (-1 ， j0) 点， N=0 ， Z=N-
闭环传递函数为：
G (s) (s) 1 G ( s) H ( s)
N (s) M (s) F (s) 1 G (s) H (s) N (s)
辅助函数：
注意：F(s)的极点是系统的开环极点，一般是 已知的；F(s)的零点是系统的闭环极点
辅助方程：F ( s ) 1 G ( s ) H ( s )
i 1 j 1
n
n
( s zi ) ( s zi ) ( s p j ) ( s p j )
i 1 i Z 1 j 1 j P 1
Z
n
P
n
Z (2 ) P(2 ) ( P Z )2
矢量总的相角增量为（净相角）：
结论： (s z1 ) 2 (s zk ) 0 (k 2,3)
(s p j ) 0 ( j 1, 2,3)
F (s) [(s z1 ) (s z2 ) (s z3 )] [(s p1 ) (s p2 ) (s p3 )]
Z
n
P
n
Z (2 ) P(2 ) ( P Z )2
P和Z分别是被封闭曲线Cs包围的特征方程函数F(s)的极点数 和零点数。上式表明，当s平面上的试验点s1沿封闭曲线Cs 顺
' 时针方向绕行一圈时，F（s）平面上对应的封闭曲线 C s 将按
逆时针方向包围坐标原点（P-Z）圈。

0
Re
G( j)H ( j)
1）F(s)对原点的包围，相当于 Gk (s) 对(-1,j0)的包围；因此映 射曲线F(s)对原点的包围次数R与Gk (s) 对(-1,j0)点的包围的次数 一样。 2）F(s)的极点就是Gk (s) 的极点，因此F(s)在右半平面的极点数 就是 Gk (s) 在右半平面的极点数。
s为复变量，以s复平面上的s=δ+jω来表示。F(s)为复变函数， 以F (s)复平面上的F (s)= u+j v表示。点映射关系，如图1所示。 s平面与F(s)平面的曲线映射关系，如图2所示。
图1
点映射关系
图2 s平面与F(s)平面的映射关系
如果在s平面上任取一条封闭曲线Cs， 且要求Cs曲线满足：曲线Cs包围F(s) 的Z个零点和P个极点。s平面上的封 闭曲线Cs如图3所示。
数应为：
R F ( s ) |开环右半极点数 F ( s ) |开环右半零点数
=P-Z
开环系统右半极点数 闭环系统右半极点数 当已知开环右半极点数时，便可由R判断闭环右极点数。
这里需要解决两个问题：
1、如何构造一个能够包围整个s右半平面的封闭曲线，并且它是 满足柯西幅角条件的？
2、如何确定相应的映射F(s)对原点的包围次数R，并将它和开环 频率特性 G j H ( j相联系？ ) 第1个问题：先假设F(s)在虚轴上没有零、极点。按顺时针方向 做一条曲线 s 包围整个s右半平面，这条封闭曲线称为奈魁斯特 围线。如下图：
奈奎斯特曲线逆时针包围（-1，j0）点的圈数R等于开 环传递函数在s右半平面的极点数P，即R=P。
说明：
（1）若P=0，系统开环稳定，闭环系统稳定的充要条件：奈 氏曲线不包围（-1，j0)点。
（2）若 R ，则系统闭环不稳定， Z=P-R。 P
[例1] 设单位反馈系统的开环传递函数如下如示，试 用奈氏判据判定闭环系统的稳定性。 解：（1）绘制 G( j的曲线。 )
F ( s ) ( s zi ) ( s p j )
i 1 j 1
n
n
( s zi ) ( s zi ) ( s p j ) ( s p j )
i 1 i Z 1 j 1 j P 1
' 令R=P-Z R为F (s)平面上封闭曲线 C逆时针包围原点的次数； s 也可写成 Z=P-R
举例说明：
s z1 s z2 s z3 设 F s s p1 s p2 s p3
j
在s平面上选择一个A点开始， z1 作一条顺时针包围某个零点 的围线 s ，其不包围也不通 过其它极点和零点。
内容提纲
第一章 控制系统的一般概念 第二章 控制系统的数学模型 第三章 控制系统的时域分析法 第四章 根轨迹法 第五章 线性系统频率响应分析 第六章 线性控制系统的频率特性校正 第七章 离散控制系统分析与设计
2018/2/21
第3讲 Nyquist稳定判据及稳定裕度
映射定理(幅角原理) Nyquist稳定判据——穿越法 Nyquist稳定判据 Bode图中的Nyquist稳定判据 开环含有积分环节 稳定裕度

它可分为三部分： Ⅰ部分是正虚轴： 0 Ⅱ部分是右半平面上半径为无穷大的半圆