下载文档原格式
![[能源化工]aspen讲义](https://img.taocdn.com/s1/m/36f0f7140640be1e650e52ea551810a6f424c859.png)
第一章前言第一节化工过程流程摸拟的基本概念一、化工过程流程模拟化工过程流程模拟就是借助计算机求解整个化工生产过程的数学模型，得到有关该化工过程的性能的信息。
二、稳态模拟和动态模拟化工流程模拟可分为稳态模拟和动态模拟。
稳态模拟是模拟一个稳态的化工生产操作过程。
一头是稳定地连续进料，中间经过一系列稳定连续的加工操作，最后从另一头稳定连续的提供出化工产品的工厂或装置都属于稳定操作过程。
我厂绝大多数生产装置都是稳态生产过程，例如，乙烯裂解装置、原油加工装置等。
动态模拟系统是模拟不稳定的生产过程，例如间歇操作反应釜的生产过程、装置的开停工过程都属于不稳定的生产过程。
目前，由于化工流程稳态模拟系统与动态模拟系统相比，较为成熟，且应用范围较广。
所以化工流程模拟一般是指化工流程稳态模拟。
三、化工过程流程模拟的应用范围化工过程流程模拟主要用于新装置的设计和指导现有装置操作。
化工过程流程模拟能够对化工过程进行稳态的热量和物料衡算、尺寸计算和费用计算、过程的技术经济评价及过程优化。
四、化工流程模拟系统化工流程模拟系统是能够用来实现化工流程模拟的一整套计算机程序，或软件系统。
五、通用和专用化工模拟系统从应用范围方面来看，化工流程模拟系统还可以分为专用的和通用的化工流程模拟系统。
专用化工流程模拟系统是针对特定流程专门开发的模拟系统，只能用于对该流程进行模拟的目的，不具有通用性。
例如，荷兰KTI公司的SPYRO软件便是一个只用于乙烯裂解炉的、稳态的、专用模拟软件。
通用化工流程模拟系统是指并非针对特定流程开发的、对不同流程均可适用的、带有通用性的化工流程模拟系统。
本课程所要讲的ASPEN PLUS 便是一个稳态的、通用化工流程模拟系统。
六、模拟系统的“三要素”系统模型、物性数据和解算方法是模拟的三个核心环节，缺一不可，亦称“模拟三要素”。
系统模型即描述化工系统性能的数学模型。
一个完整的系统模型，不仅必须包括组成此系统的各个单元模型，而且还包括能对系统结构给予明确表述的部分。
不可再分块迭代的三种收敛方法段宝颜摘要：本文主要介绍用经典的序贯模块法来解不可再分块，并设置迭代收敛框根据迭代准则直至收敛，随后又介绍了修正切断迭代变量的三种方法，直接迭代法、加权直接迭代法和严格Wegstein法。
1序贯模块法经典的序贯模块法的基本思想是环路切断后对切断流股变量进行直接迭代的方法来解不可再分块的。
以下图为例来说明序贯模块法的求解过程。
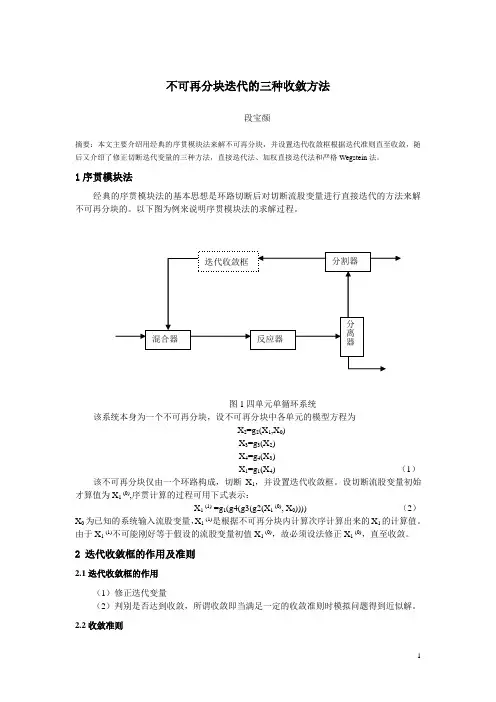
图1四单元单循环系统该系统本身为一个不可再分块，设不可再分块中各单元的模型方程为X2=g2(X1,X0)X3=g3(X2)X4=g4(X3)X1=g1(X4) （1）该不可再分块仅由一个环路构成，切断X1，并设置迭代收敛框。
设切断流股变量初始才算值为X1 (0),序贯计算的过程可用下式表示：X1 (1) =g1(g4(g3(g2(X1 (0), X0)))) （2）X0为已知的系统输入流股变量，X1 (1)是根据不可再分块内计算次序计算出来的X1的计算值。
由于X1 (1)不可能刚好等于假设的流股变量初值X1 (0)，故必须设法修正X1 (0)，直至收敛。
2 迭代收敛框的作用及准则2.1迭代收敛框的作用（1）修正迭代变量（2）判别是否达到收敛，所谓收敛即当满足一定的收敛准则时模拟问题得到近似解。
2.2收敛准则收敛准则一：在过程系统稳定模拟计算中，常用的收敛准则可以是相邻两次迭代的迭代变量绝对误差的平方和小于某一预定的误差限ε1，即Obj=∑（X j(i+1)−X j(i)）2<ε1 （3）X j(i+1)为后一次迭代的流股变量向量X1的第j个分量，X j(i)：前一次迭代的流股变量向量X1的第j个分量，这种收敛准则常因变量的分量间数量级上的差异而导致收敛上的困难。
收敛准则二：相邻两次的迭代的迭代变量相对误差的平方和小于误差极限ε2Obj=∑（X j(i+1)−X j(i)∕X j(i)）2<ε2（4）收敛准则三：相邻两次的迭代的迭代变量的加权平方和小于误差限ε3Obj=∑ωj（X j(i+1)−X j(i)）2<ε3（5）ωj：加权因子，可根据具体变量的数值大小及敏感性程度人为地决定其大小。
序贯蒙特卡洛模拟法
序贯蒙特卡洛模拟法是一种被广泛使用的数值计算方法，它被广泛用于建模和仿真数据，并在统计和金融领域中广泛应用。
下面将分步骤介绍这种方法的原理和应用。
第一步：理解基础知识
在理解序贯蒙特卡洛模拟法之前，需要先了解一些基本概念。
蒙特卡洛方法是一种随机抽样方法，用于解决复杂问题的数值计算。
序贯蒙特卡洛模拟法是一种对蒙特卡洛方法的扩展，它将多次蒙特卡洛方法运用于不同的数据集合上，以逐步改进计算结果的准确性。
第二步：应用序贯蒙特卡洛方法
序贯蒙特卡洛方法有许多实际应用。
其中一个例子是在风险评估中使用它。
在风险评估中，我们可以使用模拟数据集来模拟不同的后果。
使用序贯蒙特卡洛模拟法，我们可以逐步增加模拟的数据集的数量，以获得更准确的估计结果。
序贯蒙特卡洛模拟法可用于对股票价格的预测。
在这种情况下，我们可以使用众所周知的金融模型来创建初始数据集。
然后，我们可以使用序贯蒙特卡洛方法来逐步增加数据集的数量，以获得越来越准确的预测。
第三步：核心思想
序贯蒙特卡洛模拟法的核心思想是，通过逐步增加数据集的数量，我们可以逐步改进我们的计算结果。
每次增加数据集时，我们都会重新运行一次蒙特卡洛方法。
这样，我们可以对我们的结果进行迭代，并不断增加复杂度，从而获得数值计算的更准确结果。
第四步：总结和应用
序贯蒙特卡洛模拟法是一种高效的数值计算方法，它可以用于模拟、数据分析和风险评估等多个领域。
无论是在金融、统计学还是其它领域，序贯蒙特卡洛模拟法都可以帮助我们获得更准确的结果，并更好地理解未知数据集的属性。
P14 过程系统模拟的三种基本方法：序贯模块法、面向方程法、联立模块法。
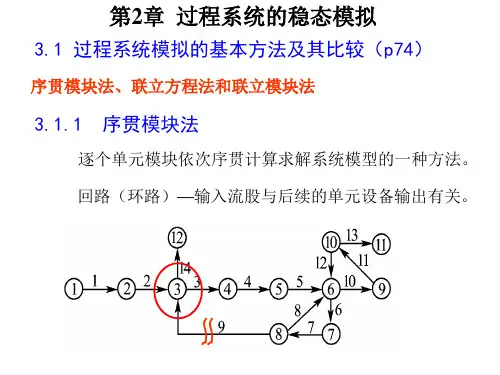
P16 序贯模块法的基本思想 (简答)从系统入口物流开始，经过接受该物流变量的单元模块的计算得到输出物流变量，作为下一个相邻单元的输入物流变量。
依此逐个的计算过程系统中的各个单元，最终计算出系统的输出物流。
计算得出过程系统中所有的物流变量值，也即状态变量值。
P16 什么叫结构单元图？利用结点和边的结合对系统结构进行数学描述，构成结构单元图或简称“图”。
图可以分成无向图和有向图。
结构单元图由结构单元与流股构成。
结构单元也称为结点，可以是一个单元设备，也可以是一个虚拟单元。
在有向图中，射入一个结点的边的数目称为该结点的入度，由一个结点射出的边数称为该结点的出度，而结点的入度与出度之和为该结点的度数。
重要的子图有以下几种:（1）路：路是图中任意两个结点之间，由其他结点和相互顺序连接的边构成的交替序列。
（2）通路：图中两个结点之间按有向边方向与其他结点连接的点、边交替序列。
（3）回路：起始结点和终止结点为同一结点时的通路，即封闭的通路。
（4）环路：除起始点外其余结点均仅通过一次的回路称为环路。
环路是网络的一个特征，这种环路的存在与过程系统中再循环反馈直接有关。
（5）相互连接的图：当图中任意一对结点均可通过路来连接时，称该图为相互连接的图。
（6）整体：是子图的一种特别重要的概念——不可再分块(整体)，通常是由多个相互关联的环路组成，这些环路具有至少一个公共结点。
（7）树：由根、枝组成，往下生长，构成数学上的“树”。
P29 EOM（面向方程法）的基本思想：描述整个过程系统的数学方程式联立求解，从而得出模拟计算结果。
把描述过程系统的所有数学模型汇集到一起，形成一个非线性方程组进行求解P30 面向方程法的核心问题是求解超大型非线性方程组，求解方法大致分为两类为：①将为求解法；②联立求解法P31 方程组的分解方法有回路搜索法和矩阵法两大类。
P54 化工过程系统通过一系列物理化学分离和化学反应（包括催化、电化与生化）改变原料状态、微观结构和/或化学组成的加工技术。
序贯蒙特卡洛模拟法1. 介绍序贯蒙特卡洛模拟法（Sequential Monte Carlo Simulation），简称SMC模拟法，是一种基于蒙特卡洛方法（Monte Carlo method）的模拟技术。
它通过多次采样和迭代，逐步逼近目标分布的方法。
SMC模拟法在金融、统计学、物理学等领域有广泛的应用，能够解决很多实际问题。
2. 基本原理SMC模拟法的基本原理是利用概率重要性采样（Importance Sampling）和粒子滤波（Particle Filtering）的组合。
它的核心思想是通过一系列粒子来近似目标分布。
每个粒子都有一个权重，用来表示其对目标分布的重要性。
具体的步骤如下：2.1 初始化首先，需要初始化一组粒子。
每个粒子都从先验分布中抽样得到，并赋予相同的权重。
2.2 权重更新接下来，通过计算每个粒子的权重来更新粒子的重要性。
权重的计算是基于观测数据和模型参数的。
通常使用似然函数来度量观测数据和模型之间的匹配程度。
2.3 重采样更新过权重之后，需要对粒子进行重采样。
重采样的目的是根据粒子的权重重新生成一组粒子，以消除权重差异。
常用的重采样方法有系统重采样、残余重采样等。
2.4 参数更新对于需要估计的模型参数，可以使用贝叶斯推断的方法来更新。
通过将粒子的权重作为先验分布，观测数据作为似然函数，可以得到参数的后验分布。
2.5 迭代重复进行权重更新、重采样和参数更新这几个步骤，直到达到收敛条件为止。
每次迭代都会逐步改善目标分布的逼近效果。
3. 应用领域SMC模拟法在很多领域都有着广泛的应用，下面介绍几个主要的应用领域：3.1 金融风险管理在金融领域，SMC模拟法可以用于风险管理和衡量。
通过建立风险模型，利用大量的随机模拟来评估金融产品的风险暴露。
这对于金融机构的风险控制和资产配置非常重要。
3.2 统计推断在统计学中，SMC模拟法可用于处理复杂的贝叶斯推断问题。
通过对参数的迭代更新，可以得到模型参数的后验分布。
1.4 过程系统模型的求解方法过程系统的模型建立后，给定系统的一组决策变量（或设计变量），通过求解过程系统的模型，就能得出全部物流的状态变量的值。
根据描述过程系统的模型不同，求解方法可以归纳为三类：①序贯模块法(Sequential Modular Method) ；②联立方程法(Equation Based Method) ；③联立模块法(Simulancous Modular Method)。
（1）序贯模块法序贯模块法是开发最早、应用最广的过程系统模拟方法。
目前绝大多数的过程系统模拟软件都属于这一类。
这种方法的基本思想是：首先建立描述过程单元的数学模块（子程序），然后根据描述过程系统流程的结构模型，确定模块的计算顺序，序贯地对各单元模块进行计算，从而完成过程系统的模拟计算。
序贯模块法的优点是与实际过程的直观联系强；模拟系统软件的建立、维护和扩充都很方便，易于通用化；计算出错时易于诊断出错位置。
其主要缺点是计算效率较低，尤其是解决设计和优化问题时计算效率更低，如图2-9所示。
虽然如此，序贯模块法仍不失为一种优秀的方法。
（2）联立方程法联立方程法又称为面向方程法，其基本思想是：将描述整个过程系统的数学方程式联立求解，从而得出模拟计算结果。
联立方程法可以根据问题的要求灵活地确定设计变量（决策变量）。
此外，联立方程法就好像把图2-9中的循环圈1~4合并成为一个循环圈(如图2-10所示)。
这种合并意味着其中所有的方程同时计算和同步收敛。
因此，联立方程法解算过程系统模型快速有效，对设计、优化问题灵活方便，效率较高。
联立方程法一直被认为是求解过程系统的理想方法，但在实践上存在一些问题。
主要在于：形成通用软件比较困难；不能利用现有大量丰富的单元模块；缺乏实际流程的直观联系；计算失败之后难于诊断错误所在；对初值的要求比较苛刻；计算技术难度较大等。
但是由于其具有显著优势，这种方法一直备受人们的青睐。
图2-9 序贯模块法的迭代循环圈图2-10 联立方程法的迭代循环圈图2-11 联立模块法的迭代循环圈(3) 联立模块法联立模块法又被称作双层法，它是集上述两种方法的优点而提出的。
不可再分块迭代的三种收敛方法
段宝颜
摘要：本文主要介绍用经典的序贯模块法来解不可再分块，并设置迭代收敛框根据迭代准则直至收敛，随后又介绍了修正切断迭代变量的三种方法，直接迭代法、加权直接迭代法和严格Wegstein法。
1序贯模块法
经典的序贯模块法的基本思想是环路切断后对切断流股变量进行直接迭代的方法来解不可再分块的。
以下图为例来说明序贯模块法的求解过程。
图1四单元单循环系统
该系统本身为一个不可再分块，设不可再分块中各单元的模型方程为
X2=g2(X1,X0)
X3=g3(X2)
X4=g4(X3)
X1=g1(X4) （1）该不可再分块仅由一个环路构成，切断X1，并设置迭代收敛框。
设切断流股变量初始才算值为X1 (0),序贯计算的过程可用下式表示：
X1 (1) =g1(g4(g3(g2(X1 (0), X0)))) （2）X0为已知的系统输入流股变量，X1 (1)是根据不可再分块内计算次序计算出来的X1的计算值。
由于X1 (1)不可能刚好等于假设的流股变量初值X1 (0)，故必须设法修正X1 (0)，直至收敛。
2 迭代收敛框的作用及准则
2.1迭代收敛框的作用
（1）修正迭代变量
（2）判别是否达到收敛，所谓收敛即当满足一定的收敛准则时模拟问题得到近似解。
2.2收敛准则
收敛准则一：在过程系统稳定模拟计算中，常用的收敛准则可以是相邻两次迭代的迭代变量绝对误差的平方和小于某一预定的误差限ε1，即
Obj=∑（X j(i+1)−X j(i)）2<ε1 （3）X j(i+1)为后一次迭代的流股变量向量X1的第j个分量，X j(i)：前一次迭代的流股变量向量X1的第j个分量，这种收敛准则常因变量的分量间数量级上的差异而导致收敛上的困难。
收敛准则二：相邻两次的迭代的迭代变量相对误差的平方和小于误差极限ε2
Obj=∑（X j(i+1)−X j(i)∕X j(i)）2<ε2（4）
收敛准则三：相邻两次的迭代的迭代变量的加权平方和小于误差限ε3
Obj=∑ωj（X j(i+1)−X j(i)）2<ε3（5）ωj：加权因子，可根据具体变量的数值大小及敏感性程度人为地决定其大小。
若在不可再分块中进行多处切断，则收敛准则应将所有迭代变量一起加以考虑，即迭代变量数等于所有切断流股的变量数之和（N st）上式应写作
O bj=∑∑ωjk（X j(i+1)−X j(i)）2≤ε4（6）k：不同的切断流股
表1序贯模块法优缺点
3 修正切断迭代变量的三种方法
修正切断迭代变量的常用方法有以下几种：直接迭代法，包括加权的直接迭代法；Wegstein法；Newton法；拟Newton法；综合算法。
3.1 直接迭代法
直接迭代法是以切断流股的初始的猜算值为起点，按类似于X1(1)=g1(g4(g3(g2(X1(0), X0)))) 的迭代格式，格式如下：
X(i+1)=F（X j(i)）
构成迭代序列进行迭代运算的。
当满足迭代收敛准则式（6）时，得到不可再分块的模拟解。
这种迭代格式实际上是解形如F（X）−X=0的方程组。
变量X的维数为切断流股的总变量数N st，显然N st远远小于整个不可再分块的总变量数。
对于图1所示的三组分系统，如果用联立方程法求解，至少（仅包括外部变量）需要解30个变量的方程组，若包括单元内部变量的话，联立解的维数还要大大增加。
而用序贯模块法则只需切断一股流股（X1），故迭代变量数仅为5。
这意味着序贯模块法将待解方程组进行了降阶处理，使求解过程变得更加容易。
直接迭代法并不总是能收敛的，其收敛性与具体描述化工过程系统模型的非线性特征有关，可以出现图2所示的四种情况，其中
a 稳定单调下降收敛
b 振荡衰减收敛
c 振荡发散
d 直接发散
图2 直接迭代的四种不同收敛情况
一维问题x=f(x)直接迭代收敛的充分条件是︱df∕dx│<1 ，即曲线f(x)的一阶导数绝对值小于1，多维是一阶偏导数矩阵绝对值小于1。
收敛情况 发散情况
图3 一维直接迭代示意图（﹡处为解）
3.2 加权直接迭代法
由于直接迭代可能会发生不收敛的情况，为了改善收敛性能，采用加权直接迭代的迭代格式
X (i+1)=QX (i)+(I−Q)F(X (i))
其中I 为N st ×N st 单位矩阵，Q —为N st ×N st 对角权矩阵，其元素为
a 稳定单调下降收敛
b 振荡衰减收敛
c 振荡发散
d 直接发散
Obj
⎩⎨
⎧==≠=j
i j i 0q ij 常数，
，
加权直接迭代法(其中W 为权矩阵)计算框图如下：
图4加权直接迭代法计算框图
3.3 严格Wegstin 法
严格Wegstin 法是一种加速迭代收敛方法。
严格Wegstin 法的迭代格式与加权直接迭代法的迭代格式在形式上完全相同，即
X (i+1)=QX (i)+(I−Q)F(X (i))
I 为Nst×Nst 单位矩阵，Q 为Nst×Nst 满秩矩阵。
几何意义：将割线取代原曲线。
图5 Wegstein 法几何示意图
割线方程的建立可以有两种不同的方法，第一次Wegstein 迭代经过两次函数计算得到。
一维迭代式及迭代过程
多维送代必须经过Nst 十1次直接送代后才能计算出迭代格式中的矩阵Q 。
简化Wegstein 法只需先用二次直接送代就简化可计算出权因子，得矩阵Q 。
由于没有考虑迭代变量间的交互影响，简化Wegstein 法的矩阵Q
为对角矩阵，它的收
()()()()
()
()()
11 ,...,2,1,1----=
=-=i j i j i j j i j j j st j j j x x x f x f s N j s s q
敛性与严格Wegstein法相比要相对差一些。
用Wegstein法时不必列出具体函数形式；
图6 严格Wegstein法计算框图
4 小结
收敛是经过反复迭代，使迭代值接近初值的过程，在切断处设置迭代收敛框，再根据迭代法计算框图得出近似值。
由于直接迭代法可能会发生不收敛的情况，为了改善收敛性能，出现了加权直接迭代法。
严格Wegstein法是一种加速迭代收敛的方法。
