机器人正运动学方程的D-H表示法
- 格式:pdf
- 大小:3.18 MB
- 文档页数:9

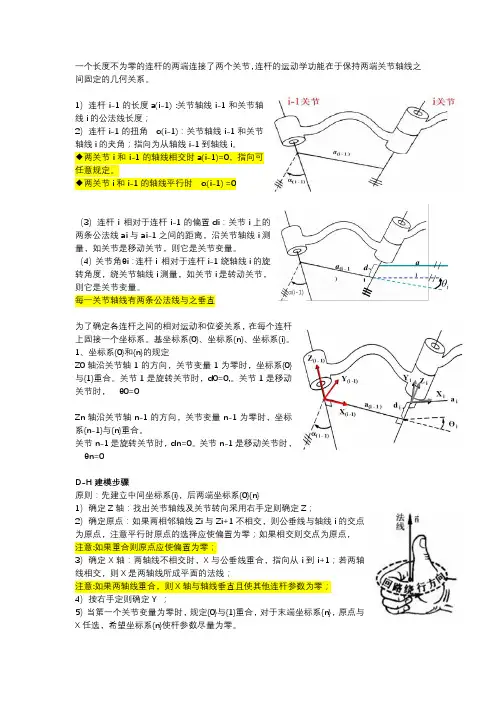
一个长度不为零的连杆的两端连接了两个关节,连杆的运动学功能在于保持两端关节轴线之间固定的几何关系。
1)连杆i-1的长度a(i-1) :关节轴线i-1和关节轴线i的公法线长度;2)连杆i-1的扭角α(i-1):关节轴线i-1和关节轴线i的夹角;指向为从轴线i-1到轴线i 。
◆两关节i和i-1的轴线相交时a(i-1)=0,指向可任意规定。
◆两关节i和i-1的轴线平行时α(i-1) =0(3)连杆i 相对于连杆i-1的偏置di:关节i上的两条公法线ai与ai-1之间的距离,沿关节轴线i测量,如关节是移动关节,则它是关节变量。
(4)关节角θi:连杆i 相对于连杆i-1绕轴线i的旋转角度,绕关节轴线i测量,如关节i是转动关节,则它是关节变量。
α(i-1)每一关节轴线有两条公法线与之垂直为了确定各连杆之间的相对运动和位姿关系,在每个连杆上固接一个坐标系。
基坐标系{0}、坐标系{n}、坐标系{i}。
1、坐标系{0}和{n}的规定Z0轴沿关节轴1的方向,关节变量1为零时,坐标系{0}与{1}重合。
关节1是旋转关节时,d0=0,。
关节1是移动关节时,θ0=0Zn轴沿关节轴n-1的方向,关节变量n-1为零时,坐标系{n-1}与{n}重合。
关节n-1是旋转关节时,dn=0。
关节n-1是移动关节时,θn=0D-H建模步骤原则:先建立中间坐标系{i},后两端坐标系{0}{n}1)确定Z轴:找出关节轴线及关节转向采用右手定则确定Z;2)确定原点:如果两相邻轴线Zi与Zi+1不相交,则公垂线与轴线i的交点为原点,注意平行时原点的选择应使偏置为零;如果相交则交点为原点,注意:如果重合则原点应使偏置为零;3)确定X轴:两轴线不相交时,X与公垂线重合,指向从i到i+1;若两轴线相交,则X是两轴线所成平面的法线;注意:如果两轴线重合,则X轴与轴线垂直且使其他连杆参数为零;4)按右手定则确定Y ;5)当第一个关节变量为零时,规定{0}与{1}重合,对于末端坐标系{n},原点与X任选,希望坐标系{n}使杆参数尽量为零。

机器人运动学(培训教材)(总49页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第2章机器人位置运动学引言本章将研究机器人正逆运动学。
当已知所有的关节变量时,可用正运动学来确定机器人末端手的位姿。
如果要使机器人末端手放在特定的点上并且具有特定的姿态,可用逆运动学来计算出每一关节变量的值。
首先利用矩阵建立物体、位置、姿态以及运动的表示方法,然后研究直角坐标型、圆柱坐标型以及球坐标型等不同构型机器人的正逆运动学,最后利用Denavit-Hartenberg(D-H)表示法来推导机器人所有可能构型的正逆运动学方程。
实际上,机器手型的机器人没有末端执行器,多数情况下,机器人上附有一个抓持器。
根据实际应用,用户可为机器人附加不同的末端执行器。
显然,末端执行器的大小和长度决定了机器人的末端位置,即如果末端执行器的长短不同,那么机器人的末端位置也不同。
在这一章中,假设机器人的末端是一个平板面,如有必要可在其上附加末端执行器,以后便称该平板面为机器人的“手”或“端面”。
如有必要,还可以将末端执行器的长度加到机器人的末端来确定末端执行器的位姿。
机器人机构机器手型的机器人具有多个自由度(DOF),并有三维开环链式机构。
在具有单自由度的系统中,当变量设定为特定值时,机器人机构就完全确定了,所有其他变量也就随之而定。
如图所示的四杆机构,当曲柄转角设定为120°时,则连杆与摇杆的角度也就确定了。
然而在一个多自由度机构中,必须独立设定所有的输入变量才能知道其余的参数。
机器人就是这样的多自由度机构,必须知道每一关节变量才能知道机器人的手处在什么位置。
图 具有单自由度闭环的四杆机构如果机器人要在空间运动,那么机器人就需要具有三维的结构。
虽然也可能有二维多自由度的机器人,但它们并不常见。
机器人是开环机构,它与闭环机构不同(例如四杆机构),即使设定所有的关节变量,也不能确保机器人的手准确地处于给定的位置。


第6期2021年2月No.6February ,2021六自由度机器人运动学及主要构件的有限元分析摘要:文章以六自由度机器人为研究对象,根据实际的作业情况,对机器人进行运动学分析以及主要构件的有限元分析。
运动学分析分为正运动学分析和逆运动学分析,解决的是机器人的手臂转向何方,分析的是手部的速度、加速度和位移。
有限元分析主要是机械系统静力学分析。
对主要构件建立模型、模型简化、网格划分,根据危险工况的受力情况,分析了各构件的应力、形变等性能,确保结构设计合理。
对于工业机器人机械结构、传动等方面,运动学和有限元分析能够判断整机设计是否达到设计目标,对结构件的优化设计具有重要的意义。
关键词:六自由度;机器人;运动学;有限元分析中图分类号:TP242.2文献标志码:A 程锴(南京以禾电子科技有限公司,江苏南京210039)作者简介:程锴(1981—),男,江苏南京人,工程师,硕士;研究方向:电子产品总体结构设计。
江苏科技信息Jiangsu Science &Technology Information引言在当前科学技术不断进步和快速发展的背景下,很多先进的技术手段被广泛应用在各个领域中[1]。
特别是机器人在工业中得到广泛的应用,在实际运行过程中,类似于码垛搬运的六自由度机器人在搬运货物中节省大量劳动力,但安全性与可靠性一直备受考验。
因此,本文主要对六自由度机器人进行运动学和静力学分析[2]。
机器人运动学研究解决的是机器人的手臂转向何方,分析的是手部的速度、加速度和位移。
运动学方程是进行机器人位移分析的基本方程,也称为位姿方程。
机器人运动学分为正运动学分析和逆运动学分析。
正运动学是机器人运用各个关节角度、各个构件车长度等已知条件来判断末端执行器在三维空间中的位置;而逆运动学正好相反,它解决的是机器人需要如何运动才能使得末端执行器到达指定位置这一问题。
静力学分析用来分析结构在给定静力载荷作用下的响应。


三自由度机械手运动学的研究【摘要】机械手的运动学分析是研究的热门话题,通过获得机械手末端装置在空间中的姿态与位置的方法,对于机械手的设计和控制极为重要。
本文通过建立一种简易设计机械手的三维模型,简单介绍了D-H方法并对该法进行了简便运算方法的分析,再结合要设计的机械手模型确定了D-H参数后,通过对机械手关节处的特征矩阵进行求解机械手运动学的正解运算,最终得到了机械手末端的姿态,并结合实际情况对末端运动坐标进行了验证。
经验证,所确定的运动函数完全符合设计的需求,对现实中机械手的生产、控制、研发等提供了可靠的理论依据。
【关键词】机械手;机器人;自由度;D-H法;正运算。
Research of Imaging System Based on STM MCUWU Xiao-lei1 WANG Shu-kun2 LI Da-peng2(1.olleg JiLin Province Design and Research Institute Petrochemical Engineering,Changchun Jilin,130022,China;2.College of Mechanical and Electrical Engineering,Changchun University of Science and Technology,Changchun Jilin,130022,China)【Abstract】Manipulator kinematics analysis is the hot topic in the research.It is of extreme importance to design and control of the manipulator through this access to get the end of the manipulator the position and posture in the space.In this paper,through the establishment of a simple 3D model design,the D-H methods were simply introduced ,combining D-H parameters model,solving the manipulator kinematics positive solution,finally gets the end of the manipulator,s posture,and connecting with the actual situation of terminal motion coordinates . Determine the movement function completely accords with the demand of this design.Provides the reliable theory basis for the production,the control of the kinematics.【Key words】Manipulator;robot;Degree of freedom;D-H method;Forward kinematics.0 引言使用机械手对工件进行搬运,目前已经得到了大范围的推广,因此研究机器手的运动,从而更好的设计和控制机器手也十分重要。

机械系统的运动学建模与动力学分析机械系统的运动学建模与动力学分析是研究机械系统运动规律和力学特性的重要领域。
运动学建模主要研究机械系统各个部件的几何关系、位姿变化和速度变化等,而动力学分析则进一步研究机械系统中各个部件之间的相互作用及其产生的力与运动之间的关系。
一、运动学建模机械系统的运动学建模是通过建立数学模型来描述机械系统的几何关系和运动规律。
在机械系统中,常见的运动学建模方法包括欧拉角法、方向余弦法、D-H法等。
1. 欧拉角法欧拉角法是一种常用的描述刚体运动的方法,它通过三个旋转角度来描述刚体的姿态变化。
欧拉角法适用于描述刚体绕固定点旋转运动的情况,如飞机的姿态控制等。
2. 方向余弦法方向余弦法是一种采用坐标系变换的方法,利用坐标系之间的转换关系来描述刚体的运动规律。
方向余弦法适用于多关节机械臂等多自由度机械系统的运动学建模。
3. D-H法D-H法(Denavit-Hartenberg法)是机器人学中常用的一种运动学建模方法。
该方法通过坐标系的定义和坐标轴的选择,将机械系统的运动规律表示为矩阵形式,方便进行分析和计算。
二、动力学分析机械系统的动力学分析是通过建立动力学方程来描述机械系统中各个部件之间的相互作用和力与运动之间的关系。
在动力学分析中,常见的方法包括拉格朗日方程法、牛顿-欧拉方程法等。
1. 拉格朗日方程法拉格朗日方程法是一种通过建立拉格朗日函数和运动方程来描述机械系统的动力学行为的方法。
该方法适用于复杂的多自由度机械系统的动力学分析,能够考虑系统的势能和动能的变化,较为准确地描述机械系统的力学特性。
2. 牛顿-欧拉方程法牛顿-欧拉方程法是一种基于牛顿定律和欧拉定理的动力学分析方法。
该方法通过建立刚体运动的动力学方程,考虑刚体的质量、惯量以及外部力矩的作用,分析机械系统的动力学特性。
三、实例分析以某机械臂为例,进行运动学建模与动力学分析。
首先,利用D-H法建立机械臂的运动学模型,确定各个关节之间的几何关系和运动规律。

工业机器人综合实验实验报告班级:姓名:学号:实验1 机器人运动学正解分析一,实验目的:掌握机器人运动学分析方法,了解机器人关节坐标空间和直角坐标空间的概念,学会使用D-H变化方法建立机器人相对坐标系,能够通过矩阵运算求取机器人的运动学正解。
实验步骤:二、实验步骤(一)、参考坐标系的建立使用Dennavit和Heartenberg提出的建模方法建立REBot-V-6R 6自由度机器人运动学坐标系(D-H 方法可以参考有关机器人学教科书),机器人6 个关节的参考坐标系如下面图所示图2-2 为D-H 参考坐标系图。
通过6自由度机器人D-H表示法参考坐标系图,得到6 自由度机器人的D-H参数表如下:由于REBot-V-6R 为具有6个旋转轴的机器人,6个旋转关节的角度作为机器人的关节变量:θ1, θ2, θ3, θ4, θ5, θ6, 其它a2,a3,d4为关节长度参数。
依照D-H 表示方法原理,可以得到坐标系x0-z0到坐标系x1-z1的变化矩阵为A1,同理相邻坐标系间的变化矩阵计为A2,A3,A4,A5,A6. 这六个坐标变化矩阵的表达式如下:(二)、运动学正解6自由度机器人的运动学正解定义为:已知6个驱动关节电机的转角(6个关节变量θ1,θ2, θ3, θ4, θ5, θ6),求取机器人末端相对于参考坐标系XYZ的位置和姿态(使用4*4 的总坐标变化矩阵表示)。
机器人末端相对于参考坐标系的位置和姿态(位姿)可以通过一系列的坐标变换得到:通过矩阵运算可以得到:三、编程验证Matlab计算程序如下:theta1=pi/2;theta2=pi/2;theta3=pi/2;theta4=0;theta5=0;theta6=0;a2=200;a3=400;d4=600;A1=[cos(theta1) 0 sin(theta1) 0;sin(theta1) 0 -cos(theta1) 0;0 1 0 0;0 0 0 1];A2=[cos(theta2) -sin(theta2) 0 a2*cos(theta2);sin(theta2) cos(theta2) 0a2*sin(theta2);0 0 1 0;0 0 0 1];A3=[cos(theta3) 0 sin(theta3) a3*cos(theta3);sin(theta3) 0 -cos(theta3)a3*sin(theta3);0 1 0 0;0 0 0 1];A4=[cos(theta4) 0 -sin(theta4) 0;sin(theta4) 0 cos(theta4) 0;0 -1 0 d4;0 0 0 1]; A5=[cos(theta5) 0 sin(theta5) 0;sin(theta5) 0 -cos(theta5) 0;0 1 0 0;0 0 0 1]; A6=[cos(theta6) -sin(theta6) 0 0;sin(theta6) cos(theta6) 0 0;0 0 1 0;0 0 0 1]; rTH=A1*A2*A3*A4*A5*A6;验证,特殊位姿下的运动学正解。


机器人D-H模型的建立摘要:随着机器人的发展,对机器人的研究日趋深入,机器人机构可以视为一种杆件机构,通过对连杆和关节的抽象,建立其运动模型和几何模型,为机器人的后续研究奠定了基础。
关键词:连杆关节几何运动学20世纪90年代以来随着空间技术海洋技术和原子能技术的迅速发展迫切需要研制出能在危险和未知环境中工作的机器人,因此工作在交互方式下的遥操作机器人开始受到广泛关注和研究。
Internet技术得到了飞速发展,正在逐步进入普及,利用Internet来作为通信介质的机器人正在日益成为研究的热点。
机器人机构可以视为一种杆件机构。
一般机器人都是由多个连杆组成,由关节将各个连杆连接起来。
关节分为转动关节、平移关节两种。
相邻的连杆在关节处可以发生平移和旋转运动。
连杆的运动一般是采用链式连接,也就是当高一级关节发生运动时会带动其下的所有连杆同时发生运动。
杆件和关节的构成方法大致可分为两种。
一种是杆件和关节是串联连接的称为串联杆件机器人或开式链机器人;而并联连接的则称为并联杆件机器人或闭式链机器人。
实际上大部分机器人都是串联杆件式机器人。
机器人的运动是由关节的运动所引起的,而关节的位置是由连杆的长度和排列方式所决定,与连杆的具体形状并没有太大的关系。
因而,我们在研究机器人的运动机理或称为机器人运动学分析时,可以对机器人进行某种抽象,将连杆抽象为一条直线,而将关节抽象为一点,对分析结果不会产生影响。
但是为了真实地仿真机器人的动作,在进行三维显示时又必须使每个杆件尽可能与实物完全一致,这样才能达到仿真的目的,这一过程称为几何建模。
对机器人的建模实际上可分为运动学建模和几何建模两部分。
但是几何建模与运动学建模实际上是密不可分的,必须根据具体情况通盘考虑。
例如为了使机器人动起来,必须对机器人的每个连杆单独建模,生成几何模型。
但同时还必须使每个几何模型保持其空间位置信息(或称之为装配),这样才能使各个连杆有机地组合在一起。
2.7机器人正运动学方程的D-H表示法在1955年,Denavit和Hartenberg在“ASME Journal of Applied Mechanics”发表了一篇论文,后来利用那个这篇论文来对机器人进行表示和建模,并导出了它们的运动方程,这已成为表示机器人和对机器人运动进行建模的标准方法,所以必须学习这部分内容。
Denavit-Hartenberg(D_H)模型表示了对机器人连杆和关节进行建模的一种非常简单的方法,可用于任何机器人构型,而不管机器人的结构顺序和复杂程度如何。
它也可用于表示已经讨论过的在任何坐标中的变换,例如直角坐标、圆柱坐标、球坐标、欧拉角坐标及RPY坐标等。
另外,它也可以用于表示全旋转的链式机器人、SCARA机器人或任何可能的关节和连杆组合。
尽管采用前面的方法对机器人直接建模会更快、更直接,但D-H表示法有其附加的好处,使用它已经开发了许多技术,例如,雅克比矩阵的计算和力分析等。
假设机器人由一系列关节和连杆组成。
这些关节可能是滑动(线性)的或旋转(转动)的,它们可以按任意的顺序放置并处于任意的平面。
连杆也可以是任意的长度(包括零),它可能被弯曲或扭曲,也可能位于任意平面上。
所以任何一组关节和连杆都可以构成一个我们想要建模和表示的机器人。
为此,需要给每个关节指定一个参考坐标系,然后,确定从一个关节到下一个关节(一个坐标系到下一个坐标系)来进行变换的步骤。
如果将从基座到第一个关节,再从第一个关节到第二个关节直至到最后一个关节的所有变换结合起来,就得到了机器人的总变换矩阵。
在下一节,将根据D-H表示法确定一个一般步骤来为每个关节指定参考坐标系,然后确定如何实现任意两个相邻坐标系之间的变换,最后写出机器人的总变换矩阵。
图2.25通用关节—连杆组合的D-H表示假设一个机器人由任意多的连杆和关节以任意形式构成。
图2.25表示了三个顺序的关节和两个连杆。
虽然这些关节和连杆并不一定与任何实际机器人的关节或连杆相似,但是他们非常常见,且能很容易地表示实际机器人的任何关节。
matlab中机器人工具箱生成d-h参数机器人工具箱(Robotics Toolbox)是MATLAB中常用的一个工具箱,用于辅助机器人的建模、仿真、控制等应用。
其中,机器人的建模主要包括如何确定机器人的d-h参数。
在机器人工具箱中,可以通过函数来自动生成机器人的d-h参数,本文将介绍在MATLAB中机器人工具箱生成d-h参数,并对其进行详细讲解。
1. 基本介绍机器人的d-h参数,全名为Denavit-Hartenberg参数,是一种用于描述机器人关节之间的位置关系的标准方法。
通过确定机器人各关节之间的距离、长度、旋转角度等属性,可以建立机器人的运动模型,进而实现机器人的运动控制等功能。
在机器人工具箱中,可以通过直接设置机器人经d-h参数来实现机器人的建模。
针对机器人的d-h参数,机器人工具箱提供了两种方法来完成参数的确定:手动输入法和自动计算法。
下面我们将依次介绍这两种方法的具体实现过程。
2. 自动计算方法机器人工具箱中提供了一系列函数,可以通过直接调用这些函数来计算机器人的d-h 参数。
这些函数主要包括:- DHparameters:用于生成机器人的d-h参数矩阵- DHFactorization:用于分解机器人的d-h参数矩阵- DYNparameters:用于计算机器人的动力学参数- Link:用于创建机器人的链接对象下面我们将以机器人Puma560为例,介绍自动生成d-h参数的具体步骤。
(1)创建链接对象在MATLAB命令行窗口中,输入以下命令:>> L1 = Link('d',0,'a',0,'alpha',pi/2,'offset',0)上述命令的作用是创建一个名为L1的链接对象,用于描述机器人的第一关节。
其中,'d'表示链接对象相对前一关节坐标系在z方向上的偏移量,'a'表示链接对象相对前一关节坐标系在x方向上的偏移量,'alpha'表示链接对象相对前一关节坐标系的旋转角度,'offset'表示链接对象的初始位移。
2.8机器人正运动学方程的D-H表示法在1955年,Denavit和Hartenberg在“ASME Journal of Applied Mechanics”发表了一篇论文,后来利用这篇论文来对机器人进行表示和建模,并导出了它们的运动方程,这已成为表示机器人和对机器人运动进行建模的标准方法,所以必须学习这部分内容。
Denavit-Hartenberg(D-H模型表示了对机器人连杆和关节进行建模的一种非常简单的方法,可用于任何机器人构型,而不管机器人的结构顺序和复杂程度如何。
它也可用于表示已经讨论过的在任何坐标中的变换,例如直角坐标、圆柱坐标、球坐标、欧拉角坐标及RPY坐标等。
另外,它也可以用于表示全旋转的链式机器人、SCARA机器人或任何可能的关节和连杆组合。
尽管采用前面的方法对机器人直接建模会更快、更直接,但D-H表示法有其附加的好处,使用它已经开发了许多技术,例如,雅克比矩阵的计算和力分析等。
假设机器人由一系列关节和连杆组成。
这些关节可能是滑动(线性)的或旋转(转动)的,它们可以按任意的顺序放置并处于任意的平面。
连杆也可以是任意的长度(包括零),它可能被弯曲或扭曲,也可能位于任意平面上。
所以任何一组关节和连杆都可以构成一个我们想要建模和表示的机器人。
为此,需要给每个关节指定一个参考坐标系,然后,确定从一个关节到下一个关节(一个坐标系到下一个坐标系)来进行变换的步骤。
如果将从基座到第一个关节,再从第一个关节到第二个关节直至到最后一个关节的所有变换结合起来,就得到了机器人的总变换矩阵。
在下一节,将根据D-H表示法确定一个一般步骤来为每个关节指定参考坐标系,然后确定如何实现任意两个相邻坐标系之间的变换,最后写出机器人的总变换矩阵。
图2.25 通用关节—连杆组合的D-H表示假设一个机器人由任意多的连杆和关节以任意形式构成。
图2.25表示了三个顺序的关节和两个连杆。
虽然这些关节和连杆并不一定与任何实际机器人的关节或连杆相似,但是他们非常常见,且能很容易地表示实际机器人的任何关节。