工程力学——第2章(力系的简化)

工程力学（静力学与材料力学）习题第2章力系的等效与简化2－1 脊柱上低于腰部的部位A是脊椎骨受损最敏感的部位，因为它可以抵抗由力F对A之矩引起的过大弯曲效应，如图所示。

已知F、d1和d2。

试求产生最大弯曲变形的角度 。

习题2－1图2－2 作用于铣刀上的力系可以简化为一个力和一个力偶。

已知力的大小为1200N，力偶矩的大小为240N·m，方向如图所示。

试求此力系对刀架固定端点O的力矩。

习题2－2图2－3 如图所示，试求F对点A的力矩。

习题2－3图习题2－6图2－4 图示作用于管板子手柄上的两个力构成一力偶，试求此力偶矩矢量。

2－5 齿轮箱有三个轴，其中A 轴水平，B 和C 轴位于yz 铅垂平面内，轴上作用的力偶如图所示。

试求合力偶。

2－6 槽钢受力如图所示。

试求此力向截面形心C 平移的结果。

2－7 截面为工字形的立柱受力如图所示。

试求此力向截面形心C 平移的结果。

2－8 平行力（F ,2F ）间距为d ，试求其合力。

2－9 已知图示一平面力系对A （3,0），B （0,4）和C （–4.5,2）三点的主矩分别为：M A = 20kN ·m ，M B = 0，M C =–10kN ·m 。

试求该力系合力的大小、方向和作用线。

习题2－4图习题2－5图习题2－7图 习题2－8图75习题2－11图2－10 空间力系如图所示，其中力偶矩M = 24N·m，作用在Oxy平面内。

试求此力系向点O简化的结果。

2－11 图示电动机固定在支架上，它受到自重160N、轴上的力120N以及力偶矩为25N·m的力偶的作用。

试求此力系向点A简化的结果。

2－12 对于图示作用在平板上的平行力系，试求其合力。

习题2－9图习题2－10图习题2－12图z2－13 试确定作用在曲轴的各曲柄销中点的力系F k（k = 1,2,...,6）是否平衡。

假定各力F i（i = 1,2, (6)的大小均为F，其作用线均通过曲轴的轴线并与之相垂直，指向背离轴线。

工程力学（静力学与材料力学）习题详细解答(第2章)习题2－2图第2章 力系的简化2－1 由作用线处于同一平面内的两个力F 和2F 所组成平行力系如图所示。

二力作用线之间的距离为d 。

试问：这一力系向哪一点简化，所得结果只有合力，而没有合力偶；确定这一合力的大小和方向；说明这一合力矢量属于哪一类矢量。

解：由习题2－1解图，假设力系向C 点简化所得结果只有合力，而没有合力偶，于是，有∑=0)(F C M ，02)(=⋅++−x F x d F ，dx =∴，F F F F =−=∴2R ，方向如图示。

合力矢量属于滑动矢量。

2－2 已知一平面力系对A (3，0)，B (0，4)和C (－4.5，2)三点的主矩分别为：M A 、M B 和M C 。

若已知：M A ＝20 kN·m 、M B ＝0和M C ＝－10kN·m ，求：这一力系最后简化所得合力的大小、方向和作用线。

解：由已知M B = 0知合力F R 过B 点；由M A = 20kN ·m ，M C = -10kN ·m 知F R 位于A 、C 间，且CD AG 2=（习题2－2解图）在图中设OF = d ，则θcot 4=dCD AG d 2)sin 3(==+θ （1） θθsin )25.4(sin d CE CD −== （2）即θθsin )25.4(2sin )3(dd −=+ d d −=+93 3=d习题2－1图习题2－1解图R∴ F 点的坐标为（-3, 0）合力方向如图所示，作用线过B 、F 点； 34tan =θ 8.4546sin 6=×==θAG 8.4R R ×=×=F AG F M A kN 6258.420R ==F 即 )kN 310,25(R=F 作用线方程：434+=x y 讨论：本题由于已知数值的特殊性，实际G 点与E 点重合。

2－3三个小拖船拖着一条大船，如图所示。

第2章 力系的简化2-1 三力作用在正方形上，各力的大小、方向及位置如图示，试求合力的大小、方向及位置。

分别以O 点和A 点为简化中心，讨论选不同的简化中心对结果是否有影响。

答： 45,N 66.5N 24===x R θ︒，合力作用线过A 点。

题2-1图 题2-2图 2-2 图示等边三角形ABC ，边长为l ，现在其三顶点沿三边作用三个大小相等的力F ，试求此力系的简化结果。

答：力偶，Fl m 23=，逆时针。

2-3 沿着直棱边作用五个力，如图示。

已知F 1＝F 3＝F 4＝F 5＝F ，F 2＝2P ，OA ＝OC ＝a ，OB ＝2a 。

试将此力系简化。

答：力偶，191),cos(,193),(cos ),cos(,19-=-===k M j M i M P a M 。

题2-3图 题2-4图2-4 图示力系中，已知F 1＝F 4＝100N ，F 2＝F 3＝1002N ，F 5＝200N ，a ＝2m ，试将此力系简化。

答：力，R ＝200 N ，与y 轴平行。

2-5 图示力系中F 1＝100N ，F 2＝F 3＝1002N ，F 4＝300N ，a ＝2m ，试求此力系简化结果。

答：力螺旋，R ＝200 N ，平行于 z 轴向下，M ＝200 N ⋅m题2-5图 题2-7图 2-6 化简力系F 1（P ，2P ，3P ）、F 1（3P ，2P ，P ），此二力分别作用在点A 1（a ，0，0）、A 2（0，a ，0）。

答： 力螺旋，3,34aP M P R ==。

2-7 求图示平行力系合力的大小和方向，并求平行力系中心。

图中每格代表1m 。

答：力，R ＝25 kN ，向下，平行力系中心（4.2, 5.4, 0）。

2-8 将题2-8中15kN 的力改为 40kN ，其余条件不变。

力系合成结果及平行力系中心将如何变化？答：力偶。

无平行力系中心。

2-9 用积分法求图示正圆锥曲面的重心。

答：h z y x C C C 31,0===。

第二章力系的简化2-1．通过A（3，0，0），B（0，4，5）两点（长度单位为米），且由A指向B的力F，在z轴上投影为，对z轴的矩的大小为。

答：F/2；62F/5。

2-2．已知力F的大小，角度φ和θ，以及长方体的边长a，b，c，则力F在轴z和y上的投影：Fz= ；Fy= ；F对轴x的矩M x(F)= 。

答：Fz=F·sinφ；Fy=－F·cosφ·cosφ；Mx（F）=F（b·sinφ+c·cosφ·cosθ）图2－40 图2－412-3．力F通过A（3，4、0），B（0，4，4）两点（长度单位为米），若F=100N，则该力在x轴上的投影为，对x轴的矩为。

答：－60N；320N.m2-4．正三棱柱的底面为等腰三角形，已知OA=OB=a，在平面ABED内有沿对角线AE 的一个力F，图中α=30°，则此力对各坐标轴之矩为：M x（F）= ；M Y（F）= ；M z（F）= 。

答：M x（F）=0，M y（F）=－Fa/2；M z（F）=6Fa/42-5．已知力F的大小为60（N），则力F对x轴的矩为；对z轴的矩为。

答：M x（F）=160 N·cm；M z（F）=100 N·cm图2－42 图2－432-6．试求图示中力F 对O 点的矩。

解：a: M O (F)=F l sin αb: M O (F)=F l sin αc: M O (F)=F(l 1+l 3)sin α+ F l 2cos αd: ()2221l l F F M o +=αsin2-7．图示力F=1000N ，求对于z 轴的力矩M z 。

题2－7图 题2－8图2-8．在图示平面力系中，已知：F 1=10N ，F 2=40N ，F 3=40N ，M=30N ·m 。

试求其合力，并画在图上（图中长度单位为米）。

解：将力系向O 点简化R X =F 2－F 1=30N R V =－F 3=－40N ∴R=50N主矩：Mo=（F 1+F 2+F 3）·3+M=300N ·m 合力的作用线至O 点的矩离 d=Mo/R=6m合力的方向：cos （R ，i ）=0.6，cos （R ，i ）=－0.8（R，i）=－53°08’（R，i）=143°08’2-9．在图示正方体的表面ABFE内作用一力偶，其矩M=50KN·m，转向如图；又沿GA，BH作用两力R、R',R=R'=502KN；α=1m。

第2章力系的简化工程力学学习指导第2章力系的简化2.1 教学要求与学习目标1. 正确掌握下列基本概念与定义：1) 力系。

2) 力系的主矢与主矩。

3) 等效的概念。

2. 正确掌握下列重要定理及其应用：1) 等效力系定理。

2) 力向一点平移定理。

3) 合力之矩定理。

3. 正确掌握并应用力系简化的基本方法。

4. 正确掌握固定端约束的性质及其约束力。

2.2 理 论 要 点2.2.1等效的概念及有关等效的原理等效力系定理：如果作用于刚体上的力系可以用另一个力系来代替，而不改变刚体的运动状态，则称这两个力系等效。

加减平衡力系原理：在已知力系上附加任意平衡力系，或除去任意平衡力系，则不改变原来力系对刚体的作用。

这一原理又叫做“加减平衡力系原理”。

它表明，加减平衡力系后，新力系与原来的力系等效。

根据这一原理，可以将已知力沿其作用线移至任意点而不改变力对物体的作用效果。

这就是所谓力的可传性。

上述有关等效的概念和加减平衡力系原理以及力的可传性，都是针对运动效果而言的，因而只适用于刚体。

当研究力对变形体所产生的变形效果时，这些都不适用。

2.2.2力向一点平移将一个力分解为一个力和力偶的过程叫做“力向一点平移”。

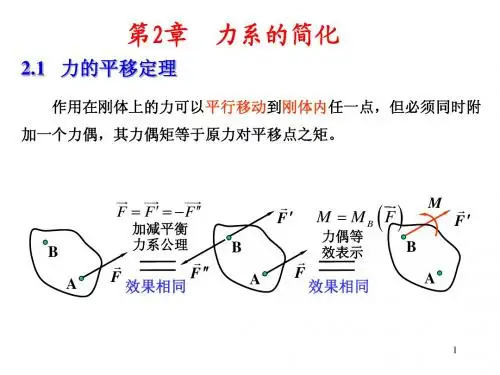
应用加减平衡力系原理，可以证明；作用于刚体上的已知力F可以向同一刚体上的任意一点平行移动，平移时需要附加一力偶，附加力偶的力偶矩M等于已知力F对平移点之矩。

力向一点平移的结果说明：作用于刚体上A点的力F与作用另一点O的力F及力偶M等效。

这也证明了力偶与力是不能等效的。

利用力向一点平移的结果不仅可以解决力系简化和平衡问题，而且在材料力学中讨论到平衡问题时，还可以将变形体视为刚体，从而可以应用上述结果，使问题简化。

但必须注意，这一结果在材料力学中应用时是要受到严格限制的。

2.2.3平面力系的简化为了得到平面力系向一点简化的结果，可以将力系中的所有力向该点平移，得到一个平面汇交力系和平面力偶系。

前者可以进一步合成一合力F R，后者则合成一合力偶M。