抽样样本量的确定_图文
- 格式:pptx
- 大小:1.99 MB
- 文档页数:85
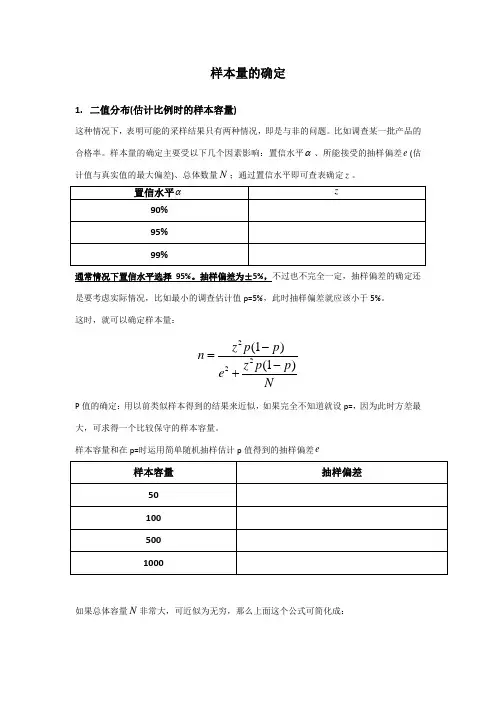
样本量的确定1. 二值分布(估计比例时的样本容量)这种情况下,表明可能的采样结果只有两种情况,即是与非的问题。
比如调查某一批产品的合格率。
样本量的确定主要受以下几个因素影响:置信水平α、所能接受的抽样偏差e (估计值与真实值的最大偏差)、总体数量N ;通过置信水平即可查表确定z 。
通常情况下置信水平选择95%。
抽样偏差为±5%,不过也不完全一定,抽样偏差的确定还是要考虑实际情况,比如最小的调查估计值p=5%,此时抽样偏差就应该小于5%。
这时,就可以确定样本量:222(1)(1)z p p n z p p e N-=-+P 值的确定:用以前类似样本得到的结果来近似,如果完全不知道就设p=,因为此时方差最大,可求得一个比较保守的样本容量。
样本容量和在p=时运用简单随机抽样估计p 值得到的抽样偏差e如果总体容量N 非常大,可近似为无穷,那么上面这个公式可简化成:22(1)z p p n e -=事实上当总体容量很小时,不会采用抽样调查,而是普查了。
2. 正态分布(估计均值时的样本容量)在这种情况下,表明采样的结果是具有多样性的,并不局限在0、1上。
比如对某一城市老年人的患病年龄进行统计。
这个时候,样本量同样受如下几个因素影响:置信水平α、所能接受的抽样偏差e (估计值与真实值的最大偏差)、总体数量N 。
样本量为:22222z S n z S e N=+S 表明的是总体标准差,这个可以用以前类似样本得到的S 或是实验调查样本的S 来近似。
同样,如果总体容量N 非常大,可近似为无穷,那么上面这个公式可简化成:222z S n e=理论基础:根据数理统计知识,样本均值对总体均值可构造如下统计量:xX uσ-,他满足标准正态分布,查表即可得到某一显著性水平下这个统计量的值,这里面的x σ表示总体均值估计量的标准误差。
在无放回简单随机抽样情况下,总体均值估计量的标准误差表达式:x σ=如果误差界限设为e ,那么:(1)n Sez N N=-解得:22222z S n z S e N=+对于二值分布,p 的总体方差为:2(1)S p p =-此时:222(1)(1)z p p n z p p e N-=-+当然,这里只考虑了简单随机抽样,对于分层抽样和整群抽样,需要再乘以一个设计效应,分层抽样效率高于简单随机抽样,效应因子小于1,整群抽样效率低于简单随机抽样,效应因子大于1.总体大小对于样本量也是有影响的,当总体个数越小时,影响越明显。







产品质量检测中的抽样与样本量确定产品质量检测是确保产品符合标准要求的关键环节。
而在进行产品质量检测时,抽样与样本量的确定是一个重要的问题。
本文将从抽样的目的、方法以及样本量确定的依据等方面进行探讨。
一、抽样的目的在进行产品质量检测时,完全检测所有产品是不现实的,同时也是不必要的。
抽样的目的是从整体中获取代表性的样本,以此推测整体的质量情况。
通过合适的抽样方法,可以减少成本和时间,同时还能够提高检测的效率。
二、抽样的方法1. 随机抽样随机抽样是指从总体中以完全随机的方式选择样本。
这种抽样方法的好处是能够消除选择偏差,使得样本具有代表性。
随机抽样可以采用抽签、随机数生成器等方式进行,确保每个样本都有平等的机会被选中。
2. 分层抽样分层抽样是基于总体的特征将总体划分为若干层次,然后从各层中抽取样本。
这种抽样方法适用于总体内部具有差异较大的情况。
通过分层抽样,可以保证样本更加具有代表性,减小误差。
3. 整群抽样整群抽样是指将总体划分为若干群体,然后从中抽取群体作为样本。
这种抽样方法适用于总体内部群体特征相似的情况。
整群抽样的优势在于简化了抽样的过程,同时也减少了误差。
三、样本量确定的依据确定合适的样本量对于产品质量检测的准确性至关重要。
样本量的确定主要需要考虑以下几个因素:1. 总体容量总体容量的大小直接影响样本量的确定。
一般来说,总体容量越大,所需样本量越大,以保证结果的准确性。
2. 置信水平置信水平是对结果的可信度的度量。
常见的置信水平有95%和99%。
置信水平越高,所需样本量越大。
3. 容忍误差容忍误差是指在样本检测时允许的误差范围。
一般来说,容忍误差越小,所需样本量越大。
4. 产品属性不同的产品属性对样本量的确定也有影响。
例如,对于质量稳定的产品,所需样本量较小;而对于质量易变的产品,所需样本量则较大。
综上所述,在产品质量检测中,抽样与样本量的确定起着重要的作用。
通过合适的抽样方法,可以提高检测效率和减少成本;而通过对样本量的合理确定,可以保证结果的准确性和可信度。

如何确定抽样方法与样本量在设计一个抽样调查时,我们通常需要做的工作是:定义总体及抽样单元、确定或构置抽样杠、选择样本量的大小、制定实施细节并实施。
在这本小册子中我们着重介绍一下定量研究的抽样和样本量这两个技术环节。
最基本的定量研究的抽样方法分为两类,一类为非概率抽样,一类为概率抽样。
一.非概率抽样非概率抽样是不能计算抽样误差的,因为它是靠调研者个人的判断来进行的抽样。
它包括偶遇抽样或者方便抽样、判断抽样、配额抽样、雪球抽样等。
偶遇抽样(方便抽样)常见的未经许可的街头随方或拦截式访问、邮寄式调查、杂志内问卷调查等都属于偶遇抽样的方式。
偶遇抽样是所有抽样技术中花费最小的(包括经费和时间)。
抽样单元是可以接近的、容易测量的、并且是合作的。
但尽管有许多优点,这种形式的抽样还是有严重的局限性。
许多可能的选择偏差都会存在,如被调查者的自我选择、抽样的主观性偏差等。
这种抽样不能代表总体的推断总体。
因此,当我们在进行街头访问或邮寄调查时,一定要谨慎对待调查结果。
判断抽样判思抽亲是基于调研者对总体的了解和经验,从总体中抽选“有代表性的”“曲型的”单位作为样本,例如从全体企业作为样本,来考察全体企业的经营状况。
如果判断准,这种方法有呆取得具有较好代表性的样本,但这种方法受主观因素影响较大。
配额抽样配额抽样是根据总体的结构特征来给调查员分派定额,以取得一个与总体结构特征大体相似的样本,例如根据人口的性别、年龄构成来给调查员规定不同性别、年龄的调查人数。
配额保证了在这些特征上样本的组成与总体的组成是一致的。
一旦配额分配好了,选择样本元素的自由度就很大了。
唯一的要求闵是所选取的元素要适合所控制的特性。
这种抽样方法的目的是使样本对总体具有更好的代表性,但仍不一定能保证样本就是有代表性的。
如果与问题相关联的某个特征是十分困难的。
另外,用这种方法进行选择严格控制调查员和调查过度程的条件下,可使配额抽样获得与某些概率抽样非常接近的结果。


抽样样本量的确定
确定样本量的方法有很多种,下面将介绍其中几种常用的方法:
1.点估计方法:这种方法假设总体参数已知或已经进行过先前的研究,通过计算得到一个点估计值,并根据误差容忍度和置信水平来计算样本量。
例如,如果要估计一个总体比例的点估计值,可以通过以下公式计算样本量:n=(Z^2*p*(1-p))/E^2,其中Z为置信水平对应的标准正态分布的分
位数,p为总体比例的估计值,E为允许的误差容忍度。
2.回归分析方法:当研究中涉及到自变量和因变量之间的关系时,可
以使用回归分析方法来确定样本量。
这个方法基于回归模型的统计力学,
通过指定预期的效应大小、误差容忍度和显著性水平来计算样本量。
3.探索性研究方法:对于探索性研究,通常没有先验的参数估计值可
以使用,因此无法使用点估计方法来确定样本量。
在这种情况下,研究者
可能需要基于经验或者判断来确定样本量。
除了以上几种方法,还有一些特殊的情况需要考虑,如多层抽样、群
组随机化实验等,这些情况下样本量的确定方法可能会有所不同。
总之,确定样本量需要综合考虑多个因素,并利用相关的统计方法来
进行计算。
在实际应用中,需要根据具体情况选择合适的方法,并确保样
本量足够大以获得可靠的统计结果。
抽样数量的确定探索性研究,样本量一般较小,而描述性研究,就需要较大的样本;收集有关许多变量的数据,样本量就要大一些;如果需要采用多元统计方法对数据进行复杂的高级分析,样本量就应当更大;如果需要特别详细的分析,如做许多分类等,也需要大样本。
针对子样本分析比只限于对总样本分析,所需样本量要大得多;总体指标的差异化越大,需要的样本量就越高;调研的精度越高,样本量越大。
简单随机抽样设计,设计效应等于1;分层抽样设计,设计效应一般小于等于1;整群或多阶抽样设计,设计效应一般大于等于1。
在实际中,在确定样本量时,不考虑时间和费用这两个极为重要的因素是不可思议的。
最终确定的样本量必须与可获得的经费预算和允许的时限保持一致。
最终样本量的确定需要在精度、费用、时限和操作的可行性等相互冲突的限制条件之间进行协调。
有关样本量的经验估计:如果是大型城市、省市一级的地区性研究,样本数在500-1000之间可能比较适合;而对于中小城市,样本量在200-300之间可能比较适合;如果是多省市或者全国性的研究,则样本量可能在1000-3000之间比较适合。
对于分组研究的每组样本量应该不少于50个。
通过试验设计所作的研究,可以采用较小的样本量。
如产品试用(留置)调查,在经费有限的情况下,可以将每组的样本量降低至30个左右,最好每组在50以上,每组超过100个可能是一种资源浪费。
样本量的计算公式:1)对于简单随机抽样,给定均值估计的精度(100%回答)简单随机抽样下,通常使用误差限和估计量的标准差来确定所需的样本量。
其中,为置信区间的值,为估计量的标准差,e为调查误差,N为总体大小。
2) 对于简单随机抽样,给定比例估计的精度(100%回答率)于是公式(1)变为:若在以往调查中可得总体比例的一个较好估计,那么直接将它代入上面的公式就可以得到所需的样本量;否则可以用,因为这时总体的方差最大。
则公式简化成市场调研中常采用该公式来确定最低样本量。