反应堆物理分析第四章课后习题

3-1.某裂变堆，快中子增殖因数1.05，逃脱共振俘获概率0.9，慢化不泄漏概率0.952，扩散不泄漏概率0.94，有效裂变中子数1.335，热中子利用系数0.882，试计算其有效增殖因数和无限介质增殖因数。

解：无限介质增殖因数： 1.1127k pf εη∞==不泄漏概率：0.9520.940.89488s d Λ=ΛΛ=×=有效增殖因数：0.9957eff k k ∞=Λ=3-2.H 和O 在1000eV 到1eV 能量范围内的散射截面近似为常数，分别为20b 和38b 。

计算H 2O 的ξ以及在H 2O 中中子从1000eV 慢化到1eV 所需的平均碰撞次数。

解：不难得出，H2O 的散射截面与平均对数能降应有下述关系：σH2O ∙ξH2O =2σH ∙ξH +σO ∙ξO即：(2σH +σO )∙ξH2O =2σH ∙ξH +σO ∙ξOξH2O =（2σH ∙ξH +σO ∙ξO ）/(2σH +σO )查附录3，可知平均对数能降：ξH =1.000，ξO =0.120，代入计算得：ξH2O =(2×20×1.000+38×0.120)/(2×20+38)=0.571可得平均碰撞次数：Nc =ln(E 2/E 1)/ξH2O =ln(1000/1)/0.571=12.09≈12.13-3.在讨论中子热化时，认为热中子源项Q(E)是从某给定分界能E c 以上能区的中子，经过弹性散射慢化而来的。

设慢化能谱服从Ф(E)=Ф/E 分布，试求在氢介质内每秒每单位体积内由E c 以上能区，（1）散射到能量E （E<E c ）的单位能量间隔内之中子数Q(E)；（2）散射到能量区间ΔE g =E g-1-E g 内的中子数Q g 。

解：（1）由题意可知：()(')(')(')'cE s Q E E E f E E dE φ∞=Σ→∫对于氢介质而言，一次碰撞就足以使中子越过中能区，可以认为宏观截面为常数：/()(')(')'cE s E a Q E E f E E dE φ=Σ→∫在质心系下，利用各向同性散射函数：。

第一章思考题1.压水堆为什么要在高压下运行？2.水在压水堆中起什么作用？3.压水堆与沸水堆的主要区别是什么？4.压水堆主冷却剂系统都包括哪些设备？5.一体化压水堆与分散式的压水堆相比有哪些优缺点？6.重水堆使用的核燃料富集度为什么可以比压水堆的低？7.在同样的堆功率情况下，重水堆的堆芯为什么比压水堆的大？8.气冷堆与压水堆相比有什么优缺点？9.石墨气冷堆中的百墨是起什么作用的？10.快中子堆与热中子堆相比有哪些优缺点？11.快中子堆在核能源利用方面有什么作用？12.回路式制冷堆与池式饷冷堆的主要区别是什么？13.在使用铀作为反应堆冷却剂时应注意些什么问题？14.快中子堆内使用的燃料富集度为什么要比热中子反应堆的高？第二章思考题1.简述热中子反应堆内中子的循环过程。

2.为什么热中子反应堆中通常选用轻水作慢化齐IJ?3.解释扩散长度、中子年龄的物理意义。

4.述反射层对反应堆的影响。

5.简述反应性负温度系数对反应堆运行安全的作用。

6.解释“腆坑”形成的过程。

7.什么是反应堆的燃耗深度和堆芯寿期？8.大型压水堆通常采取哪些方法控制反应性？9.简述缓发中子对反应堆的作用。

10.简述反应性小阶跃变化时反应堆内中子密度的响应。

第三章思考题1.能用于压水反应堆的易裂变同位素有哪些，它们分别是怎样生成的？2.为什么在压水堆内不直接用金属铀而要用陶瓷U02作燃料？3.简述U02的熔点和热导率随温度、辐照程度的变化情况。

4.简述U02芯块中裂变气体的产生及释放情况。

5.燃料元件的包壳有什么作用？6.对燃料包壳材料有哪些基本要求？目前常用什么材料？7.为什么错合金用作包壳时，其使用温度要限制在350℃以下？8.何谓错合金的氢脆效应，引起氢脆效应的氢来源何处？9.错合金包壳的氢脆效应有何危害，应如何减轻这种不利影响？10.什么是U02燃料芯块的肿胀现象，应采取什么防范措施？11.控制棒直径较细有什么好处？12.定位格架采用什么材料制戚，为什么？13.定位格架有何功用？14.对用作控制棒的材料有什么基本要求？15.通常用作控制棒的元素和材料有哪些？16.简单说明Ag-In-Cd控制材料的核特性。

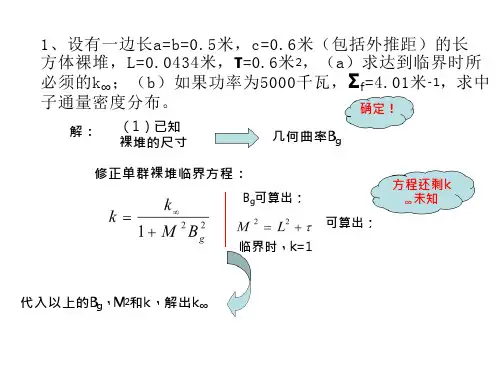
核反应堆物理分析习题答案第四章第四章1.试求边长为a,b,c (包括外推距离)的长⽅体裸堆的⼏何曲率和中⼦通量密度的分布。

设有⼀边长a =b 0.5m,c=0.6m (包括外推距离)的长⽅体裸堆，L= 0.043m,.=6 10~m 2o ( 1)求达到临界时所必须的 k ：- ；( 2)如果功率为5000kW 〕f = 4.01m -1，求中⼦通量密度分布。

其中：M 2 =L 2.= 0.00248m 2⼆ k ：： -1.264求出通量表达式中的常系数 0只须2_2 2-2 22?设⼀重⽔⼀铀反应堆的堆芯k ：：=1.28,L =1.8 10 m,~1.20 10 m 。

试按单群理论，修正单群理论的临界⽅程分别求出该芯部的材料曲率和达到临界时候的总的中⼦不泄露⼏率。

解：对于单群理论:解: 长⽅体的⼏何中⼼为原点建⽴坐标系，则单群稳态扩散⽅程为：D 俘⼸ +专)—E a ? + y 0 :x :y :z边界条件： (a/2,y,z) (x,b/2,z) = (x, y,c/2) =0(以下解题过程都不再强调外推距离，可认为所有外边界尺⼨已包含了外推距离) 因为三个⽅向的通量拜年话是相互独⽴的，利⽤分离变量法：*(x, y,z)=X(x)Y(y)Z(z)V 2X V 2Y V 2Z a — 1 将⽅程化为：⼀X Y Z设：空“竺⼀B y ,空XY yZL 2想考虑X ⽅向，利⽤通解：X(x) = AcosB x X ? Csin B x Xan 兀代⼊边界条件：Acos(B x ⼆)=0= B nx,n =1,3.5,...-2aii J[同理可得： (x, y,z)⼆ 0cos(-x)cos(—y)cos(-z)a aaJIB1x :a其中0是待定常数。

(1) 2其⼏何曲率：B g应⽤修正单群理论，临界条件变为: 2 2(_)2=106.4m ， ck ：： -1 _ B 2M2 g(2) JIJI2、3P = E f l ⽡f ?dV = E f ￡ f % J ；cos(—x)dx J b cos(「y)dy J c 2 cos(— z)dz = E f 》f %abc (⼆)~2-2 b P(2)31.007 101Ef j abc8m_g — 1材料曲率1 1在临界条件下：2 22 2 ⼀0.78131 B ：L 21 B ；L 2(或⽤⼆=1 k ：：)2 2 2对于单群修正理论： M =L ：；r =0.03mBM ⼆等1 = 9.33m 谡1 1在临界条件下：2 22 2= 0.78131 + B ：M 21+B ：M 2(注意：这时能⽤-I =1 k-,实际上在维持临界的前提条件下修正理论不会对不泄露⼏率产⽣影响，但此时的⼏何曲率、⼏何尺⼨已发⽣了变化，不再是之前的系统了。

核反应堆物理分析答案第一章1-1.某压水堆采用UO 2作燃料，其富集度为2.43%（质量），密度为10000kg/m3。

试计算：当中子能量为0.0253eV 时，UO 2的宏观吸收截面和宏观裂变截面。

解：由18页表1-3查得，0.0253eV 时：(5)680.9,(5)583.5,(8) 2.7a f a U b U b U b σσσ=== 由289页附录3查得，0.0253eV 时：()0.00027b a O σ=以c 5表示富集铀内U -235与U 的核子数之比，ε表示富集度，则有：555235235238(1)c c c ε=+-151(10.9874(1))0.0246c ε-=+-=255283222M(UO )235238(1)162269.91000()() 2.2310()M(UO )Ac c UO N N UO m ρ-=+-+⨯=⨯==⨯所以，26352(5)() 5.4910()N U c N UO m -==⨯ 28352(8)(1)() 2.1810()N U c N UO m -=-=⨯2832()2() 4.4610()N O N UO m -==⨯2112()(5)(5)(8)(8)()()0.0549680.9 2.18 2.7 4.460.0002743.2()()(5)(5)0.0549583.532.0()a a a a f f UO N U U N U U N O O m UO N U U m σσσσ--∑=++=⨯+⨯+⨯=∑==⨯=1-2.某反应堆堆芯由U -235,H 2O 和Al 组成，各元素所占体积比分别为0.002,0.6和0.398，计算堆芯的总吸收截面(E=0.0253eV)。

解：由18页表1-3查得，0.0253eV 时： (5)680.9a U b σ=由289页附录3查得，0.0253eV 时：112() 1.5,() 2.2a a Al m H O m --∑=∑=,()238.03,M U =33()19.0510/U kg m ρ=⨯可得天然U 核子数密度283()1000()/() 4.8210()A N U U N M U m ρ-==⨯则纯U -235的宏观吸收截面：1(5)(5)(5) 4.82680.93279.2()a a U N U U m σ-∑=⨯=⨯=总的宏观吸收截面：120.002(5)0.6()0.398()8.4()a a a a U H O Al m -∑=∑+∑+∑=1-3、求热中子（0.025电子伏）在轻水、重水、和镉中运动时，被吸收前平均遭受的散射碰撞次数。

反应堆物理习题答案反应堆物理习题答案反应堆物理是核能工程领域中的重要学科，它研究核反应堆中的裂变过程、中子输运、反应性能以及热工水力等问题。

在学习反应堆物理的过程中，习题是不可或缺的一部分。

通过解答习题，我们可以更好地理解和掌握反应堆物理的基本原理和计算方法。

下面是一些常见的反应堆物理习题及其答案。

习题一：某核反应堆的中子速度分布函数为：f(v) = 0.5e^(-0.5v) ，其中v为中子速度，单位为km/s。

求该反应堆中中子的平均速度。

解答：中子的平均速度可以通过计算速度分布函数的加权平均值得到。

即v_avg = ∫v*f(v)dv= ∫v*0.5e^(-0.5v)dv= -2e^(-0.5v)(2+v)|0到∞= 4 km/s因此，该反应堆中中子的平均速度为4 km/s。

习题二：某反应堆的裂变截面为σ_f = 1.5×10^(-24) cm^2，吸收截面为σ_a = 0.8×10^(-24) cm^2，散射截面为σ_s = 0.7×10^(-24) cm^2。

求该反应堆的中子繁殖比。

解答：中子繁殖比是衡量反应堆裂变能源释放程度的重要参数，可以通过裂变截面和吸收截面的比值来计算。

即k = σ_f / σ_a= (1.5×10^(-24) cm^2) / (0.8×10^(-24) cm^2)= 1.875因此，该反应堆的中子繁殖比为1.875。

习题三：某反应堆的热功率为1000 MW，裂变截面为σ_f = 1.8×10^(-24)cm^2，每次裂变释放的平均能量为E_f = 200 MeV。

求该反应堆每秒发生的裂变事件数。

解答：反应堆的热功率可以通过裂变截面、每次裂变释放的平均能量和裂变事件数的乘积来计算。

即P = σ_f * E_f * N= (1.8×10^(-24) cm^2) * (200 MeV) * N= (1.8×10^(-24) cm^2) * (200×10^6 eV) * N= (1.8×10^(-24) cm^2) * (200×10^6 × 1.6×10^(-19) J) * N= 5.76×10^(-3) J * N由于1 MW = 10^6 J/s，所以1000 MW = 10^9 J/s。

核反应堆物理分析答案第一章1-1.某压水堆采用UO 2作燃料，其富集度为2.43%（质量），密度为10000kg/m3。

试计算：当中子能量为0.0253eV 时，UO 2的宏观吸收截面和宏观裂变截面。

解：由18页表1-3查得，0.0253eV 时：(5)680.9,(5)583.5,(8) 2.7a f a U b U b U b σσσ=== 由289页附录3查得，0.0253eV 时：()0.00027b a O σ=以c 5表示富集铀内U-235与U 的核子数之比，ε表示富集度，则有：555235235238(1)c c c ε=+-151(10.9874(1))0.0246c ε-=+-=255283222M(UO )235238(1)162269.91000()() 2.2310()M(UO )Ac c UO N N UO m ρ-=+-+⨯=⨯==⨯所以，26352(5)() 5.4910()N U c N UO m -==⨯ 28352(8)(1)() 2.1810()N U c N UO m -=-=⨯2832()2() 4.4610()N O N UO m -==⨯2112()(5)(5)(8)(8)()()0.0549680.9 2.18 2.7 4.460.0002743.2()()(5)(5)0.0549583.532.0()a a a a f f UO N U U N U U N O O m UO N U U m σσσσ--∑=++=⨯+⨯+⨯=∑==⨯=1-2.某反应堆堆芯由U-235,H 2O 和Al 组成，各元素所占体积比分别为0.002,0.6和0.398，计算堆芯的总吸收截面(E=0.0253eV)。

解：由18页表1-3查得，0.0253eV 时： (5)680.9a U b σ=由289页附录3查得，0.0253eV 时：112() 1.5,() 2.2a a Al m H O m --∑=∑=,()238.03,M U =33()19.0510/U kg m ρ=⨯可得天然U 核子数密度283()1000()/() 4.8210()A N U U N M U m ρ-==⨯则纯U-235的宏观吸收截面：1(5)(5)(5) 4.82680.93279.2()a a U N U U m σ-∑=⨯=⨯=总的宏观吸收截面：120.002(5)0.6()0.398()8.4()a a a a U H O Al m -∑=∑+∑+∑=1-3、求热中子（0.025电子伏）在轻水、重水、和镉中运动时，被吸收前平均遭受的散射碰撞次数。

核反应堆物理分析答案第一章1-1.某压水堆采用UO 2作燃料，其富集度为2.43%（质量），密度为10000kg/m3。

试计算：当中子能量为0.0253eV 时，UO 2的宏观吸收截面和宏观裂变截面。

解：由18页表1-3查得，0.0253eV 时：(5)680.9,(5)583.5,(8) 2.7a f a U b U b U b σσσ=== 由289页附录3查得，0.0253eV 时：()0.00027b a O σ=以c 5表示富集铀内U-235与U 的核子数之比，ε表示富集度，则有：555235235238(1)c c c ε=+-151(10.9874(1))0.0246c ε-=+-=255283222M(UO )235238(1)162269.91000()() 2.2310()M(UO )Ac c UO N N UO m ρ-=+-+⨯=⨯==⨯所以，26352(5)() 5.4910()N U c N UO m -==⨯ 28352(8)(1)() 2.1810()N U c N UO m -=-=⨯2832()2() 4.4610()N O N UO m -==⨯2112()(5)(5)(8)(8)()()0.0549680.9 2.18 2.7 4.460.0002743.2()()(5)(5)0.0549583.532.0()a a a a f f UO N U U N U U N O O m UO N U U m σσσσ--∑=++=⨯+⨯+⨯=∑==⨯=1-2.某反应堆堆芯由U-235,H 2O 和Al 组成，各元素所占体积比分别为0.002,0.6和0.398，计算堆芯的总吸收截面(E=0.0253eV)。

解：由18页表1-3查得，0.0253eV 时： (5)680.9a U b σ=由289页附录3查得，0.0253eV 时：112() 1.5,() 2.2a a Al m H O m --∑=∑=,()238.03,M U =33()19.0510/U kg m ρ=⨯可得天然U 核子数密度283()1000()/() 4.8210()A N U U N M U m ρ-==⨯则纯U-235的宏观吸收截面：1(5)(5)(5) 4.82680.93279.2()a a U N U U m σ-∑=⨯=⨯=总的宏观吸收截面：120.002(5)0.6()0.398()8.4()a a a a U H O Al m -∑=∑+∑+∑=1-61171721111PV V 3.210P 2101.2510m 3.2105 3.210φφ---=∑⨯⨯⨯===⨯∑⨯⨯⨯⨯1-12题每秒钟发出的热量： 69100010 3.125100.32PTE J η⨯===⨯ 每秒钟裂变的U235：109193.12510 3.125109.765610()N =⨯⨯⨯=⨯个运行一年的裂变的U235：1927'N T 9.765610365243600 3.079710()N =⨯=⨯⨯⨯⨯=⨯个 消耗的u235质量：27623A (1)'(10.18) 3.079710235m A 1.422810g 1422.8kg N 6.02210N α++⨯⨯⨯=⨯==⨯=⨯ 需消耗的煤： 9967E'110365243600m 3.398310Kg 3.398310Q 0.32 2.910⨯⨯⨯⨯===⨯=⨯⨯⨯吨 1-10.为使铀的η＝1.7，试求铀中U-235富集度应为多少(E=0.0253eV)。