【精品】核反应堆物理分析习题答案第四章
- 格式：doc
- 大小：1.04 MB
- 文档页数：12
下载文档原格式
合集下载
核反应堆物理分析 (谢仲生 吴宏春 张少泓 著) 西安交大、原子能出版社 课后答案4
3-1.某裂变堆，快中子增殖因数1.05，逃脱共振俘获概率0.9，慢化不泄漏概率0.952，扩散不泄漏概率0.94，有效裂变中子数1.335，热中子利用系数0.882，试计算其有效增殖因数和无限介质增殖因数。
解：无限介质增殖因数： 1.1127k pf εη∞==不泄漏概率：0.9520.940.89488s d Λ=ΛΛ=×=有效增殖因数：0.9957eff k k ∞=Λ=3-2.H 和O 在1000eV 到1eV 能量范围内的散射截面近似为常数，分别为20b 和38b 。
计算H 2O 的ξ以及在H 2O 中中子从1000eV 慢化到1eV 所需的平均碰撞次数。
解：不难得出，H2O 的散射截面与平均对数能降应有下述关系：σH2O ∙ξH2O =2σH ∙ξH +σO ∙ξO即：(2σH +σO )∙ξH2O =2σH ∙ξH +σO ∙ξOξH2O =（2σH ∙ξH +σO ∙ξO ）/(2σH +σO )查附录3，可知平均对数能降：ξH =1.000，ξO =0.120，代入计算得：ξH2O =(2×20×1.000+38×0.120)/(2×20+38)=0.571可得平均碰撞次数：Nc =ln(E 2/E 1)/ξH2O =ln(1000/1)/0.571=12.09≈12.13-3.在讨论中子热化时，认为热中子源项Q(E)是从某给定分界能E c 以上能区的中子，经过弹性散射慢化而来的。
设慢化能谱服从Ф(E)=Ф/E 分布，试求在氢介质内每秒每单位体积内由E c 以上能区，（1）散射到能量E （E<E c ）的单位能量间隔内之中子数Q(E)；（2）散射到能量区间ΔE g =E g-1-E g 内的中子数Q g 。
解：（1）由题意可知：()(')(')(')'cE s Q E E E f E E dE φ∞=Σ→∫对于氢介质而言，一次碰撞就足以使中子越过中能区，可以认为宏观截面为常数：/()(')(')'cE s E a Q E E f E E dE φ=Σ→∫在质心系下，利用各向同性散射函数：。
反应堆物理分析-第四章课后习题
有效增殖系数keff
（b） 已知系统达临界，keff=1
栅格参数k∞、
L2、τ
临界理论
材料曲率Bm
几何曲率Bg 对于圆柱形裸堆
临界时， 几何曲率=材料曲率
已经有了Bg2 和R，解出H
即可
（c）
反射层尺寸 + 堆芯尺寸 等效裸堆
快中子不 泄漏几率
等效裸堆的Bg’2
裸堆临界理论
热中子不 泄漏几率
加装反射层后的keff
反应堆临界对曲 率的要求是：
（3）年龄理论临界方程：
k∞，L2，τ已知，代入
算出Bg，也就算出了 Bm
比较六因子公式和一下三种理论的临界方程：
六因子公式
单群理论临界方程：
单群临界的扩散不泄漏项
单群临界中，中子均考虑为 热中子，因此并没有慢化泄
漏项
六因子公式
双群理论临界方程：
单群临界理论的扩散不泄漏项 考虑到慢化后的不泄漏项
临界时，芯部几何曲率
求出Bc2
对于纯U5组成的堆芯：
在以上的过程中，已经求出了堆芯尺寸R 堆芯临界体积：
堆芯临界质量：
六因子公式
年龄理论临界方程：
单群临界的扩散的不泄漏项
考虑到慢化到热中子年龄τ引起的泄漏项
3、设有圆柱形铀- 水栅装置，R=0.50米，水位高度H=1.0米，设
栅格参数为：k∞=1.19，L2=6.6×10-4米2，τ=0.50×10-2米2。（a）
试求该装置的有效增殖系数k；（b）当该装置恰好达临界时，水
位高度H等于多少？（c）设某压水堆以该铀- 水栅格作为芯部，
堆芯的尺寸为R=1.66米，H=3.50米，若反射层节省估算为δ r=0.07米，δH=0.1米。试求反应堆的初始反应性ρ以及快中子不
核反应堆物理分析习题答案第四章
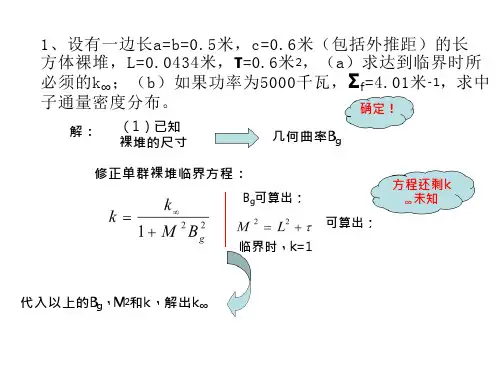
第四章1.试求边长为,,a b c （包括外推距离）的长方体裸堆的几何曲率和中子通量密度的分布。
设有一边长0.5,0.6a b m c m ===（包括外推距离）的长方体裸堆，0.043,L m =42610m τ-=⨯。
（1）求达到临界时所必须的k ∞；（2）如果功率为15000, 4.01f kW m -∑=，求中子通量密度分布。
解：长方体的几何中心为原点建立坐标系，则单群稳态扩散方程为：222222()0a a D k x y zφφφφφ∞∂∂∂++-∑+∑=∂∂∂ 边界条件： (/2,,)(,/2,)(,,/2)0a y z x b z x y c φφφ===（以下解题过程都不再强调外推距离，可认为所有外边界尺寸已包含了外推距离） 因为三个方向的通量拜年话是相互独立的，利用分离变量法：(,,)()()()x y z X x Y y Z z φ=将方程化为：22221k X Y ZX Y Z L∞-∇∇∇++=- 设：222222,,x y z X Y Z B B B X Y Z∇∇∇=-=-=- 想考虑X 方向，利用通解：()cos sin x x X x A B x C B x =+代入边界条件：1cos()0,1,3.5,...2x nx x a n A B B n B a aππ=⇒==⇒=同理可得：0(,,)cos()cos()cos()x y z x y z aaaπππφφ=其中0φ是待定常数。
其几何曲率：22222()()()106.4g B m a b cπππ-=++=（1）应用修正单群理论，临界条件变为：221g k B M∞-= 其中：2220.00248M L m τ=+=1.264k ∞⇒=（2）只须求出通量表达式中的常系数0φ3222002222cos()cos()cos()()a bc a b c f f f f f f VP E dV E x dx y dy z dz E abc a b c πππφφφπ---=∑=∑=∑⎰⎰⎰⎰3182102() 1.00710f f P m s E abcπφ--⇒==⨯∑2.设一重水—铀反应堆的堆芯222221.28, 1.810, 1.2010k L m m τ--∞==⨯=⨯。
核反应堆物理基础Chapter4
二、反应性温度效应 (4)
2.3 慢化剂的反应性温度系数
慢化剂温度变化时影响慢化剂的慢化能力，主要途径如下： 慢化剂温度变化时影响慢化剂的慢化能力，主要途径如下： 慢化剂密度变化。以水为例，温度升高慢化能力降低， 慢化剂密度变化。以水为例，温度升高慢化能力降低，能谱变 硬。 慢化剂温度变化引起中子温度变化。温度升高时能谱变硬。 慢化剂温度变化引起中子温度变化。温度升高时能谱变硬。 对于热中子反应堆来讲，一般情况下，能谱变硬时，反应性降低。 对于热中子反应堆来讲，一般情况下，能谱变硬时，反应性降低。因 为能谱变硬时，燃料的共振吸收增加，裂变材料的裂变截面降低， 为能谱变硬时，燃料的共振吸收增加，裂变材料的裂变截面降低，中 子泄漏也会有所增加。但这并非是绝对的。影响反应性有诸多因素。 子泄漏也会有所增加。但这并非是绝对的。影响反应性有诸多因素。 各种因素因为能谱的变化进而影响反应性的趋势不尽相同， 各种因素因为能谱的变化进而影响反应性的趋势不尽相同，要看最后 的综合效果，也看反应堆的设计。 的综合效果，也看反应堆的设计。有些强吸收体的中子截面呈 1/v 变 化规律。能谱变硬时，吸收能力减弱，引起反应性增加。 化规律。能谱变硬时，吸收能力减弱，引起反应性增加。如果这种吸 收作用在反应堆中占主导地位，则总的反应性温度系数就会是正的。 收作用在反应堆中占主导地位，则总的反应性温度系数就会是正的。
二、反应性温度效应 (1)
2.1 反应性温度系数 反应性温度系数(1) 反应堆停堆时处于常温状态，即冷态。 反应堆停堆时处于常温状态，即冷态。运行时 温度升高到运行温度。 温度升高到运行温度。材料温度的改变一般情况下 对反应性有很大的影响。温度变化一个单位(K, C) 对反应性有很大的影响。温度变化一个单位 带来的反应性变化定义为反应性温度系数α 带来的反应性变化定义为反应性温度系数 T： αT = dρ/dT = dK/dT /K2 ≈ dK/dT /K 反应堆内温度的变化是不均匀的， 反应堆内温度的变化是不均匀的，各种材料温 度变化对反应性的影响也不尽相同， 度变化对反应性的影响也不尽相同，所以温度的变 化要有所指，如燃料温度，慢化剂温度等。 化要有所指，如燃料温度，慢化剂温度等。对应的 温度系数称为燃料反应性温度系数， 温度系数称为燃料反应性温度系数，慢化剂反应性 温度系数等。 温度系数等。
核反应堆物理分析修订版(课后习题答案)
2
由于外推距离很小可以忽略，可以只考虑堆体积内的吸收反应率： Ra
a
( x , y , z ) dxdydz
2a
ቤተ መጻሕፍቲ ባይዱ
0 .274 3 10 17 ( 1 .55 10 s
19 1
)3
(
a a ) 2 2
3-9，解：根据课本中（3-23）式和（3-24）式得：
第一章 核反应堆的核物理基础
1-2，解： 235U 单位体积内的原子核数：
N 235U 19.05 106 6.02 1028 4.88 1028 m 3 ， a, 235U 680.9 10 28 m 2 235
通过以上方法求，也可以查附录 3 得：
H 2 O 单位体积内的分子数： N H 2O 3.34 10 28 m 3 ， a, H 2O 0.664 10 28 m 2 ；
当 A>10 时
( A 1) 2 A 1 )， ln =1+ ln ( 1 A 1 2A
2
。
2 A 3
所以 H =1+
( A 1) 2 A 1 ) 1， ln ( 2A A 1
2 2 A 3
=0.12。
H O =
2
2 H H O O 0.57。 2 H O
293 （ TM 为介质的温度 570 K ） 6.1m 1 ， TM
计算此反应堆的慢化能力：
S N H O ( S ) H O N Al ( S ) Al N
2 2
235
U
( S )U 1.16m 1
课本中（2-79）中子温度： Tn TM (1 C
由于外推距离很小可以忽略，可以只考虑堆体积内的吸收反应率： Ra
a
( x , y , z ) dxdydz
2a
ቤተ መጻሕፍቲ ባይዱ
0 .274 3 10 17 ( 1 .55 10 s
19 1
)3
(
a a ) 2 2
3-9，解：根据课本中（3-23）式和（3-24）式得：
第一章 核反应堆的核物理基础
1-2，解： 235U 单位体积内的原子核数：
N 235U 19.05 106 6.02 1028 4.88 1028 m 3 ， a, 235U 680.9 10 28 m 2 235
通过以上方法求，也可以查附录 3 得：
H 2 O 单位体积内的分子数： N H 2O 3.34 10 28 m 3 ， a, H 2O 0.664 10 28 m 2 ；
当 A>10 时
( A 1) 2 A 1 )， ln =1+ ln ( 1 A 1 2A
2
。
2 A 3
所以 H =1+
( A 1) 2 A 1 ) 1， ln ( 2A A 1
2 2 A 3
=0.12。
H O =
2
2 H H O O 0.57。 2 H O
293 （ TM 为介质的温度 570 K ） 6.1m 1 ， TM
计算此反应堆的慢化能力：
S N H O ( S ) H O N Al ( S ) Al N
2 2
235
U
( S )U 1.16m 1
课本中（2-79）中子温度： Tn TM (1 C
核反应堆物理分析课后习题及答案
核反应堆物理分析答案第一章1-1.某压水堆采用UO 2作燃料，其富集度为2.43%（质量），密度为10000kg/m3。
试计算：当中子能量为0.0253eV 时，UO 2的宏观吸收截面和宏观裂变截面。
解：由18页表1-3查得，0.0253eV 时：(5)680.9,(5)583.5,(8) 2.7a f a U b U b U b σσσ=== 由289页附录3查得，0.0253eV 时：()0.00027b a O σ=以c 5表示富集铀内U -235与U 的核子数之比，ε表示富集度，则有：555235235238(1)c c c ε=+-151(10.9874(1))0.0246c ε-=+-=255283222M(UO )235238(1)162269.91000()() 2.2310()M(UO )Ac c UO N N UO m ρ-=+-+⨯=⨯==⨯所以，26352(5)() 5.4910()N U c N UO m -==⨯ 28352(8)(1)() 2.1810()N U c N UO m -=-=⨯2832()2() 4.4610()N O N UO m -==⨯2112()(5)(5)(8)(8)()()0.0549680.9 2.18 2.7 4.460.0002743.2()()(5)(5)0.0549583.532.0()a a a a f f UO N U U N U U N O O m UO N U U m σσσσ--∑=++=⨯+⨯+⨯=∑==⨯=1-2.某反应堆堆芯由U -235,H 2O 和Al 组成，各元素所占体积比分别为0.002,0.6和0.398，计算堆芯的总吸收截面(E=0.0253eV)。
解：由18页表1-3查得，0.0253eV 时： (5)680.9a U b σ=由289页附录3查得，0.0253eV 时：112() 1.5,() 2.2a a Al m H O m --∑=∑=,()238.03,M U =33()19.0510/U kg m ρ=⨯可得天然U 核子数密度283()1000()/() 4.8210()A N U U N M U m ρ-==⨯则纯U -235的宏观吸收截面：1(5)(5)(5) 4.82680.93279.2()a a U N U U m σ-∑=⨯=⨯=总的宏观吸收截面：120.002(5)0.6()0.398()8.4()a a a a U H O Al m -∑=∑+∑+∑=1-3、求热中子（0.025电子伏）在轻水、重水、和镉中运动时，被吸收前平均遭受的散射碰撞次数。
核工后半学期答案汇总
φΣ f V
312 ×10
8
5000 ×103 =
, y, z ) 1.0036 ×1014 cos( φ ( x=
第四章第 4 题
π
50
x) cos(cos(
π
50
y )(
π
60
一个球形裸堆，其中燃料铀 235 均匀分布在石墨中。碳－铀原子数之比
NC = 10000 ，试用单群临界理论估算此堆 NU
混合物中碳－铀的重量比＝
235＋10000 × 12 ＝511.638 , 235
3
据此可以算出混合物的密度是 1.60286 克/cm ，与纯石墨的密度相差不到千分之二。
1.60286 ×
碳的核密度＝
511.638 511.638＋1 × 6.022 × 1023 ＝ 0.08028 × 1024/cm 3 与前面算出的值几乎没有差别。 12
1 ) Lr
同样分离变量：
∇ 2φ (r ) ∇ 2φ ( z ) + = κ2 φ (r ) φ ( z) ∇ 2φ (r ) = − Br2 φ (r )
分离的结果是：
其解的形式也是零阶贝塞尔函数，同芯部一样！这一点多少有点出人意料，反射层是无源方程，怎么与芯部方程的 解的形式一样呢？甚至连曲率也一样？其实不怪， 因为径向形状一样、 尺寸一样， 因为要满足同样的外推边界条件。
讨论：用（1）除以（3） ，可以消去a 3 ，用（2）除以（4） ，可以消去a 4 ，剩下两个系数a 1 和a 2 ，以a 1 和a 2 作为未
知数写出：
a1 a = 0 2
临界方程就是系数行列式为零。再经过化简，得到临界公式是：
Dc Bz BH BH DB tg ( z ) th(κ T1 ) tg ( z ) + c z th(κ T1 ) 2 2 Dc κ Dc κ = − DB BH BH DB 1 − c z tg ( z ) th(κ T2 ) tg ( z ) + c z th(κ T2 ) 2 2 Dc κ Dc κ 1−
核反应堆物理分析课后习题参考答案
核反应堆物理分析答案第一章1-1.某压水堆采用UO 2作燃料，其富集度为2.43%（质量），密度为10000kg/m3。
试计算：当中子能量为0.0253eV 时，UO 2的宏观吸收截面和宏观裂变截面。
解：由18页表1-3查得，0.0253eV 时：(5)680.9,(5)583.5,(8) 2.7a f a U b U b U b σσσ=== 由289页附录3查得，0.0253eV 时：()0.00027b a O σ=以c 5表示富集铀内U-235与U 的核子数之比，ε表示富集度，则有：555235235238(1)c c c ε=+-151(10.9874(1))0.0246c ε-=+-=255283222M(UO )235238(1)162269.91000()() 2.2310()M(UO )Ac c UO N N UO m ρ-=+-+⨯=⨯==⨯所以，26352(5)() 5.4910()N U c N UO m -==⨯ 28352(8)(1)() 2.1810()N U c N UO m -=-=⨯2832()2() 4.4610()N O N UO m -==⨯2112()(5)(5)(8)(8)()()0.0549680.9 2.18 2.7 4.460.0002743.2()()(5)(5)0.0549583.532.0()a a a a f f UO N U U N U U N O O m UO N U U m σσσσ--∑=++=⨯+⨯+⨯=∑==⨯=1-2.某反应堆堆芯由U-235,H 2O 和Al 组成，各元素所占体积比分别为0.002,0.6和0.398，计算堆芯的总吸收截面(E=0.0253eV)。
解：由18页表1-3查得，0.0253eV 时： (5)680.9a U b σ=由289页附录3查得，0.0253eV 时：112() 1.5,() 2.2a a Al m H O m --∑=∑=,()238.03,M U =33()19.0510/U kg m ρ=⨯可得天然U 核子数密度283()1000()/() 4.8210()A N U U N M U m ρ-==⨯则纯U-235的宏观吸收截面：1(5)(5)(5) 4.82680.93279.2()a a U N U U m σ-∑=⨯=⨯=总的宏观吸收截面：120.002(5)0.6()0.398()8.4()a a a a U H O Al m -∑=∑+∑+∑=1-3、求热中子（0.025电子伏）在轻水、重水、和镉中运动时，被吸收前平均遭受的散射碰撞次数。
核反应堆物理分析课后习题参考答案
核反应堆物理分析答案第一章1-1.某压水堆采用UO 2作燃料，其富集度为2.43%（质量），密度为10000kg/m3。
试计算：当中子能量为0.0253eV 时，UO 2的宏观吸收截面和宏观裂变截面。
解：由18页表1-3查得，0.0253eV 时：(5)680.9,(5)583.5,(8) 2.7a f a U b U b U b σσσ=== 由289页附录3查得，0.0253eV 时：()0.00027b a O σ=以c 5表示富集铀内U-235与U 的核子数之比，ε表示富集度，则有：555235235238(1)c c c ε=+-151(10.9874(1))0.0246c ε-=+-=255283222M(UO )235238(1)162269.91000()() 2.2310()M(UO )Ac c UO N N UO m ρ-=+-+⨯=⨯==⨯所以，26352(5)() 5.4910()N U c N UO m -==⨯ 28352(8)(1)() 2.1810()N U c N UO m -=-=⨯2832()2() 4.4610()N O N UO m -==⨯2112()(5)(5)(8)(8)()()0.0549680.9 2.18 2.7 4.460.0002743.2()()(5)(5)0.0549583.532.0()a a a a f f UO N U U N U U N O O m UO N U U m σσσσ--∑=++=⨯+⨯+⨯=∑==⨯=1-2.某反应堆堆芯由U-235,H 2O 和Al 组成，各元素所占体积比分别为0.002,0.6和0.398，计算堆芯的总吸收截面(E=0.0253eV)。
解：由18页表1-3查得，0.0253eV 时： (5)680.9a U b σ=由289页附录3查得，0.0253eV 时：112() 1.5,() 2.2a a Al m H O m --∑=∑=,()238.03,M U =33()19.0510/U kg m ρ=⨯可得天然U 核子数密度283()1000()/() 4.8210()A N U U N M U m ρ-==⨯则纯U-235的宏观吸收截面：1(5)(5)(5) 4.82680.93279.2()a a U N U U m σ-∑=⨯=⨯=总的宏观吸收截面：120.002(5)0.6()0.398()8.4()a a a a U H O Al m -∑=∑+∑+∑=1-61171721111PV V 3.210P 2101.2510m 3.2105 3.210φφ---=∑⨯⨯⨯===⨯∑⨯⨯⨯⨯1-12题每秒钟发出的热量： 69100010 3.125100.32PTE J η⨯===⨯ 每秒钟裂变的U235：109193.12510 3.125109.765610()N =⨯⨯⨯=⨯个运行一年的裂变的U235：1927'N T 9.765610365243600 3.079710()N =⨯=⨯⨯⨯⨯=⨯个 消耗的u235质量：27623A (1)'(10.18) 3.079710235m A 1.422810g 1422.8kg N 6.02210N α++⨯⨯⨯=⨯==⨯=⨯ 需消耗的煤： 9967E'110365243600m 3.398310Kg 3.398310Q 0.32 2.910⨯⨯⨯⨯===⨯=⨯⨯⨯吨 1-10.为使铀的η＝1.7，试求铀中U-235富集度应为多少(E=0.0253eV)。
核反应堆热工水力分析第四章习题
核反应堆热工水力分析第四章习题第一步，计算等温流的摩擦压降。
等温时，回路的摩擦压降由试验段的摩擦压降1f p ∆和其他管段的摩擦压降2f p ∆组成。
（1）根据回路运行压力16p MPa =，水温260t C =°，查表得水的密度0ρ和粘性系数0µ。
（2）对试验段：直径10013d .m =，流速15V m s =，管长112L .m =，计算雷诺数11010d V Re ρµ=，查表4-1得到工业用钢管的粗糙度0046.mm ε=，故可算出1d ε，结合1Re ，查莫迪图4-1得到摩擦系数1f ，用Darcy 公式计算摩擦压降2111112f L V p f d ρ∆=（3）对其他管段：直径10025d .m =，管长21L L L =−，总管长18L m =。
根据连续性方程计算其他管段的流速2V 1122AV A V =，故211211222A d V V V A d ==计算雷诺数22020d V Re ρµ=，根据2d ε，结合2Re ，查莫迪图4-1，得到摩擦系数2f ，用Darcy 公式计算摩擦压降2222222f L V p f d ρ∆=（4）计算回路的摩擦压降：12f f f p p p ∆∆∆=+第二步，计算试验段加热的回路压降。
回路压降p ∆应包括摩擦压降f p ∆，提升压降el p ∆，加速压降a p ∆和弯头的形阻压降c p ∆。
（1）摩擦压降c p ∆：回路的摩擦压降c p ∆由试验段的摩擦压降1f p ∆，热交换器段的摩擦压降2f p ∆，其他管段的摩擦压降3f p ∆构成。
对试验段，进口温度1260f ,in t C =°，出口温度1300f ,out t C =°，主流温度1112f ,in f ,outf t t t +=。
根据运行压力16p MPa =，试验段主流温度1f t ，查表得水的密度1ρ，粘性系数1µ，普朗特数1Pr 和比热1p c 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四章1.试求边长为,,a b c （包括外推距离)的长方体裸堆的几何曲率和中子通量密度的分布.设有一边长0.5,0.6a b m c m ===（包括外推距离）的长方体裸堆，0.043,L m =42610m τ-=⨯。
（1）求达到临界时所必须的k ∞；（2）如果功率为15000, 4.01f kW m -∑=，求中子通量密度分布.解:长方体的几何中心为原点建立坐标系，则单群稳态扩散方程为:222222()0a a D k x y zφφφφφ∞∂∂∂++-∑+∑=∂∂∂边界条件：(/2,,)(,/2,)(,,/2)0a y z x b z x y c φφφ===（以下解题过程都不再强调外推距离,可认为所有外边界尺寸已包含了外推距离）因为三个方向的通量拜年话是相互独立的，利用分离变量法：(,,)()()()x y z X x Y y Z z φ=将方程化为：22221k X Y ZX Y Z L∞-∇∇∇++=- 设：222222,,x y z X Y Z B B B X Y Z∇∇∇=-=-=- 想考虑X 方向,利用通解：()cos sin x x X x A B x C B x =+代入边界条件：1cos()0,1,3.5,...2x nx x a n A B B n B a aππ=⇒==⇒=同理可得：0(,,)cos()cos()cos()x y z x y z a a aπππφφ=其中0φ是待定常数。
其几何曲率：22222()()()106.4g B m a b cπππ-=++=(1)应用修正单群理论，临界条件变为：221g k B M∞-= 其中:2220.00248M L m τ=+=1.264k ∞⇒=（2）只须求出通量表达式中的常系数0φ3222002222cos()cos()cos()()a bc a b c f f f f f f VP E dV E x dx y dy z dz E abc a b c πππφφφπ---=∑=∑=∑⎰⎰⎰⎰3182102() 1.00710f f P m s E abcπφ--⇒==⨯∑2.设一重水—铀反应堆的堆芯222221.28, 1.810, 1.2010k L m m τ--∞==⨯=⨯.试按单群理论，修正单群理论的临界方程分别求出该芯部的材料曲率和达到临界时候的总的中子不泄露几率。
解:对于单群理论：在临界条件下：2222110.781311g m B L B LΛ===++ （或用1k ∞Λ=）对于单群修正理论:2220.03M L m τ=+=22219.33M k B m L-∞-==在临界条件下:2222110.781311g m B M B M Λ===++ (注意：这时能用1k ∞Λ=，实际上在维持临界的前提条件下修正理论不会对不泄露几率产生影响,但此时的几何曲率、几何尺寸已发生了变化，不再是之前的系统了。
）4.设有圆柱形铀—水栅装置，R=0。
50米，水位高度H=1。
0米,设栅格参数为：k ∞=1。
19，L 2=6.6×10-4米2，τ=0.50×10-2米2.（a)试求该装置的有效增殖系数k ；（b)当该装置恰好达临界时,水位高度H 等于多少?（c)设某压水堆以该铀-水栅格作为芯部，堆芯的尺寸为R=1。
66米，H=3。
50米，若反射层节省估算为δr =0。
07米，δH =0.1米。
试求反应堆的初始反应性ρ以及快中子不泄漏几率和热中子不泄漏几率.5。
一个球壳形反应堆，内半径为1R ,外半径为2R ，如果球的内、外均为真空，求证单群理论的临界条件为:11211tan tan 1tan BR BR BR BR BR -=+解答:以球心为坐标原点建立球坐标系，单群稳态扩散方程：2222B r r r φφφ∂∂+=-∂∂边界条件:i 。
1lim 0;x R J →= ii.2()0R φ=(如果不2R 包括了外推距离的话，所得结果将与题意相悖） 球域内方程通解：cos sin ()Br Brr A Cr rφ=+ 由条件i 可得：111111221111cos sin sin cos lim 0r R r R BR BR BR BR J D ABA CBC R R R R φ=→=-∇ =---=1111111111cos sin tan sin cos tan 1BR BR BR BR BR C A A BR BR BR BR BR --⇒==-++由条件ii 可得:由此可见，11211tan tan tan 1BR BR BR BR BR -=+,证毕。
7。
一由纯235U 金属33(18.710/)kg m ρ=⨯组成的球形快中子堆，其周围包以无限厚的纯 238U 33(19.010/)kg m ρ=⨯，试用单群理论计算其临界质量，单群常数如下：23512381: 1.5, 1.78,35.4, 2.51;:0,0.18,35.4f a tr f a tr U b b m v U b m σσσσ--==∑====∑=。
解：以球心为左边原点建立球左边系，对于U-235和U —238分别列单群稳态扩散方程，设其分界面在半径为R 处：255251235:k U L φφ∞--∇=-方程1 288281238:U L φφ-∇=方程2 边界条件：i 。
50lim r φ→<∞ii.58()()R R φφ=iii.5858r R r R D D r rφφ==∂∂ = ∂∂iv.8lim 0r φ→∞= 令2251k B L ∞-=(。
在此临界条件下,既等于材料曲率,也等于几何曲率），球域内方程1通解：555cos sin ()Br Brr A C r rφ=+ 由条件i 可知50A =，所以：5sin ()Brr C rφ=球域内方程2通解：88888exp(/)exp(/)()r L r L r A C r r φ-=+ 由条件iv 可知，所以：888exp(/)()r L r A rφ-=由条件ii 可得：88exp(/)exp(/)sin sin R L R L BRC A C AR R BR--=⇒= 由条件iii 可得：888582885(1)exp()cos sin 11()()exp()sin cos R RD L L BR BR RD C B D A C A R R L R R L D BR BR BR+--=---⇒=-所以（由题目已知参数,5,858,5,81133tr tr tr tr D D ∑=∑⇒===∑∑） 888858(1)exp()exp(/)sin cos (1)sin sin cos sin R R L L D R L R A A BR BR BR BR BR BR BR D BR L +--=⇒-=+-即：8cos sin RBR BR BR L -=88cot(1/)1cos sin arc BL BR BR R BL B -=-⇒=代入数据：328358510 4.7910AN N m M ρ--==⨯328388810 4.8110AN N m M ρ--==⨯,5,5,5,52325,5,5218883555 2.1151 1.3110329.170.1043cot(1/)/2arctan(1/)0.06474421.33f f a a a f v v k L m B m L marc BL BL R mB Bm V R kgσσπρρπ∞--∑===∑==⨯∑∑====-+=====⨯=8.试证明有限高半圆形反应堆中子通量密度分布和几何曲率11(,)()sin cos()x r z r z AJ R H πφμθ=2221()()g x B R Hπ=+ 其中:1 3.89x =是11()J x 的第一个零点，即。
证明：（1）书上图4—8所示的柱坐标系下，单群稳态扩散方程可写为（临界条件下，几何曲率与材料曲率相等)：2222222211,(0,0,/2/2)g B r R H Z H r r r r zφφφφφθπθ∂∂∂∂+++=-≤≤≤≤-≤≤∂∂∂∂边界条件（不考虑外推距离）：i.00r R r φφ== = =II 。
00θθπφφ== = = III./2/20z H z H φφ==- = =(注意,这里不能用线性微分方程解的存在唯一性定理：如果()(1,2,,),()i a t i n f t =⋅⋅⋅/都是区间[],a b 上的连续函数，则对于任一0(,)t a b ∈及任意的(0)(1)(2)(1)0000,,,,n x x x x -⋅⋅⋅方程：()()11()n n n n x a x a x a x f t -'++⋅⋅⋅++=存在唯一解()x t ϕ=定义于区间[],a b 上，且满足初值条件()()00()(0,,1),k k x t x k n ==⋅⋅⋅- 而此扩散方程并非线性微分方程。
）对于表达式：111(,,)()sin cos(), 3.89x r zr z AJ x R Hπφθθ== 不难证明其满足上述全部三个边界条件.11((0)(3.89)0)J J ==（2）将表达式代入方程,其中，已知如下条件： 101,nn n xJ nJ xJ J J -''=-+=- 可推得:101J xJ J x-+'= []10001001110011222212(1)J xJ J J J xJ J J J J xJ J J J x x x x x x x x-+-+''''=-+-++=--+-=--111111110()()()()x r J x r x r x x r R J J J R R r R R'''==-+1220211111111111102211()22()()1()()()()()x r J x r x r x r x x r x r x r x r R J J J J J x r x r R R R R r R R R R RR ⎧⎡⎤⎫⎪⎢⎥⎪⎪⎡⎤⎛⎫⎡⎤'''''==--=--⎨⎬⎢⎥ ⎪⎢⎥⎢⎥⎣⎦⎝⎭⎣⎦⎪⎪⎢⎥⎪⎣⎦⎭⎩所以：2211111022112()()()x x r x r x r J J r R R R R r x r J R φφ⎡⎤⎛⎫∂--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦∂=11110111()()()x r x x r J J r r R Rr R x r J Rφφ∂-+∂=2112221111()()x r J r r R x r J Rφθφ∂∂=-所以：11221121111111002222222111()()211()()()()()()x r x r J J x x r x r x r x r x r R RJ J J x r rR R R R r R R rr r r r x r RJ Rφφφθφ⎡⎤∂∂∂---+-++⎢⎥⎣⎦∂∂∂==-再有：2222cos()()cos()z F H z z H Hππφππφ⎛⎫∂- ⎪⎝⎭∂==- 所以方程为：2221g x B R H π⎛⎫⎛⎫--=- ⎪ ⎪⎝⎭⎝⎭可知该表达式为方程的解。