核反应堆物理分析复习资料

第一章核反应堆的核物理基础（6学时）1.什么是核能？包括哪两种类型？核能的优点和缺点是什么？核能：原子核结构发生变化时释放出的能量，主要包括裂变能和聚变能。

优点：1）污染小：2）需要燃料少；3）重量轻、体积小、不需要空气，装一炉料可运行很长时间。

缺点：1）次锕系核素具有几百万年的半衰期，且具有毒性，需要妥善保存；2）裂变产物带有强的放射性，但在300年之内可以衰变到和天然易裂变核素处于同一放射性水平上；3）需要考虑排除剩余发热。

2.核反应堆的定义。

核反应堆可按哪些进行分类，可划分为哪些类型？属于哪种类型的核反应堆？核反应堆：一种能以可控方式产生自持链式裂变反应的装置。

核反应堆分类：3.原子核基本性质。

核素：具有确定质子数Z和核子数A的原子核。

同位素：质子数Z相同而中子数N不同的核素。

同量素：质量数A相同，而质子数Z和中子数N各不相同的核素。

同中子数：只有中子数N相同的核素。

原子核能级：最低能量状态叫做基态，比基态高的能量状态称激发态。

激发态是不稳定的，会自发跃迁到基态，并以放出射线的形式释放出多余的能量。

核力的基本特点：1）核力的短程性2）核力的饱和性3）核力与电荷无关4.原子核的衰变。

包括：放射性同位素、核衰变、衰变常数、半衰期、平均寿命的定义；理解衰变常数的物理意义；核衰变的主要类型、反应式、衰变过程，穿透能力和电离能力。

放射性同位素：不稳定的同位素，会自发进行衰变，称为放射性同位素。

核衰变：有些元素的原子核是不稳定的，它能自发而有规律地改变其结构转变为另一种原子核，这种现象称为核衰变，也称放射性衰变。

衰变常数：它是单位时间内衰变几率的一种量度；物理意义是单位时间内的衰变几率，标志着衰变的快慢。

半衰期：原子核衰变一半所需的平均时间。

平均寿命：任一时刻存在的所有核的预期寿命的平均值。

5.结合能与原子核的稳定性。

包括：质量亏损、结合能和比结合能的定义；理解释放能量的两种途径。

质量亏损：核子（质子和中子）结合构成原子后总质量减少。

西安交通大学——核反应堆物理分析(共470题)从反应堆物理的角度看，良好的慢化剂材料应具有什么样的性能？答案：慢化剂是快中子与它的核发生碰撞后能减速成热中子的材料，这与它的三种中子物理性能有关：δ－平均对数能量缩减；Σs－宏观散射截面；Σa－宏观吸收截面。

综合评价应是δ和Σs都比较大而Σa又较小的材料才是较好的慢化材料，定量地用慢化能力δΣs和慢化比δ和Σs/Σa来比较。

试列出常用慢化剂的慢化能力和慢化比。

核力所具有的特点是什么？答案：基本特点是：核力是短程力，作用范围大约是1～2×10-13cm；核力是吸引力，中子与中子，质子与中子，质子与质子之间均是强吸引力。

核力与电荷无关。

核力具有饱和性，每一核子只与其邻近的数目有限的几个核子发生相互作用。

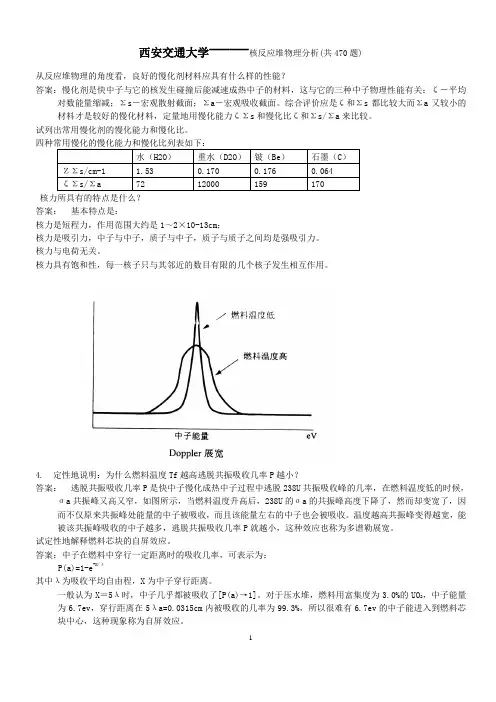
4. 定性地说明：为什么燃料温度Tf越高逃脱共振吸收几率P越小？答案：逃脱共振吸收几率P是快中子慢化成热中子过程中逃脱238U共振吸收峰的几率，在燃料温度低的时候，ζa共振峰又高又窄，如图所示，当燃料温度升高后，238U的ζa的共振峰高度下降了，然而却变宽了，因而不仅原来共振峰处能量的中子被吸收，而且该能量左右的中子也会被吸收。

温度越高共振峰变得越宽，能被该共振峰吸收的中子越多，逃脱共振吸收几率P就越小，这种效应也称为多谱勒展宽。

试定性地解释燃料芯块的自屏效应。

答案：中子在燃料中穿行一定距离时的吸收几率，可表示为：P(a)=1-e-X/λ其中λ为吸收平均自由程，X为中子穿行距离。

一般认为X＝5λ时，中子几乎都被吸收了[P(a)→1]。

对于压水堆，燃料用富集度为3.0%的UO2，中子能量为6.7ev，穿行距离在5λa=0.0315cm内被吸收的几率为99.3%，所以很难有6.7ev的中子能进入到燃料芯块中心，这种现象称为自屏效应。

6. 什么是过渡周期？什么是渐近周期？答案：在零功率时，当阶跃输入－正反应性ρ0（ρ0<β）后，反应堆功率的上升速率（或周期）是随ρ0输入后的时间t而改变的（如图所示）。

核反应堆物理分析各章节重要知识点整理汇总资料第一章1、在反应堆内中子与原子的相互作用方式主要有：势散射、直接相互作用和复合核的形成。

其中复合核的形成是中子和原子相互作用的最重要方式。

2、复合核的衰变分解的方式有：共振弹性散射、共振非弹性散射、辐射俘获和核裂变，可以概括为散射和吸收。

3、共振现象：但入射中子的能量具有某些特定值，恰好使形成的复合核激发态接近于某个量子能级时，中子被靶核吸收而形成复合核的概率就显著增加，这种现象就叫作共振现象。

4、非弹性散射特点：只有当入射中子的动能高于靶核的第一激发态的能量时才能使靶核激发，也就是说，只有入射中子的能量高于某一数值时才能发生非弹性散射，由此可知，非弹性散射具有阈能的特点。

5、弹性散射特点：它可以分为共振弹性散射和势散射两种，区别在于前者经过复合核的形成过程，后者则没有。

在热中子反应堆内，对中子从高能慢化到低能的过程起主要作用的是弹性散射。

6、易裂变同位素：一些核素，如233U 、235U 、239Pu 和241Pu 等核素在各种能量的中子作用下均能发生裂变，并且在低能中子作用下发生裂变的可能性较大，通常把它们称为易裂变同位素。

7、可裂变同位素：同位素232Th 、238U 和240Pu 等只有在能量高于某一阈值的中子作用下才发生裂变，通常把它们称为可裂变同位素。

8、中子束强度I ：在单位时间内，通过垂直于中子飞行方向的单位面积的中子数量，记为I 。

9、单位体积中的原子核数N ：计算公式为AN N ρ0=0N ：阿伏加德罗常数，取值为6.0221367*1023/molρ：材料密度A ：该元素的原子量10、微观截面σ：微观截面是表示平均一个给定能量的入射中子与一个靶核发生作用的概率大小的一种度量，通常用“巴恩”（b ）作为单位，1b=10-28m 2。

11、核反应下标：s--散射；a--吸收；γ--辐射俘获；f--裂变；t--总核反应 12、靶内平行中子束强度：Nx e I x I σ-=0)(13、宏观截面∑：宏观截面是一个中子与单位体积内所有原子核发生核反应的平均概率大小的一种度量，单位为m -1,公式为：σN =∑由几种元素组成的均匀混合物质的宏观截面x ∑：∑=∑ixi i x N σ14、富集度：某种元素在其同位素中的（原子）重量百分比。

核反应堆物理复习第一章 反应堆的核物理基础1.原子是保持物质化学性质的最小微粒，它由原子核和核外电子组成，而原子核又由核子组成，核子包括质子和中子。

2. 元素：质子数相同的所有原子。

同位素：质子数相同、中子数不同的同一元素的不同原子。

核素：具有特定质子数、中子数和核能态，且平均寿命长到足以被观测到的原子。

3.核力的特点：（1）近程性；（2）饱和性；（3）与电荷无关性；（4）强相互作用。

4.α衰变：放射性核素的原子核自发地放射出α粒子，变成另一种核素的原子核的物理过程。

或者说，有些不稳定核衰变时放出由2个质子、2个中子组成的α粒子的物理过程。

X Z A →Y Z−2A−4+α+Q α （α：He 24） Ra 88226→Rn 86222+He 24β-衰变：放射性核素的原子核自发地放射出β-粒子，变成另一种核素的原子核的物理过程。

或者说，核内中子多于质子的不稳定核，中子自发转化成一个质子和一个电子，同时放出反中微子，从而变得相对稳定的物理过程。

X Z A →Y Z+1A +β-+v ̅+Q β− （β-：e −10，v ̅—反中微子） O 819→F 919+β- +v ̅ β+衰变：放射性核素的原子核自发地放射出β+粒子，变成另一种核素的原子核的物理过程。

或者说，核内质子多于中子的不稳定核，核俘获一个轨道电子，这个电子同一质子结合形成一个中子，相当于核放出一个正电子和一个中微子的物理过程。

X Z A →Y Z−1A +β+ +v+Q β+ （β+：e +10，v —中微子） O 815→N 715+β+ +vγ衰变：激发态的原子核不稳定，通过放出γ光子的形式，向较低激发态或基态跃迁的过程。

X Z Am →X Z A +Q γ Kr 3683m →Kr 3683+Q γ自发裂变：指处在基态或同核异能态的原子核在没有受到外来粒子或能量的情况下发生的裂变。

例如现在很多压水堆核电厂都采用能自发裂变的252Cf （锎）作为初级中子源。

第1章—核反应堆物理分析中子按能量分为三类: 快中子(E ﹥0.1 MeV),中能中子(1eV ﹤E ﹤0.1 MeV),热中子(E ﹤1eV).共振弹性散射 A Z X + 01n → [A+1Z X]* → A Z X + 01n 势散射 A Z X + 01n → A Z X + 01n 辐射俘获是最常见的吸收反应.反应式为 A Z X + 01n → [A+1Z X]* → A+1Z X + γ235U 裂变反应的反应式 23592U + 01n → [23692U]* → A1Z1X + A2Z2X +ν01n微观截面 ΔI=-σIN Δx /I I IIN x N xσ-∆-∆==∆∆ 宏观截面 Σ= σN 单位体积内的原子核数 0N N Aρ=中子穿过x 长的路程未发生核反应，而在x 和 x+dx 之间发生首次核反应的概率P(x)dx= e -Σx Σdx核反应率定义为 R nv =∑ 单位是 中子∕m 3⋅s 中子通量密度nv ϕ=总的中子通量密度Φ 0()()()n E v E dE E dE ϕ∞∞Φ==⎰⎰平均宏观截面或平均截面为 ()()()EEE E dERE dEϕϕ∆∆∑∑==Φ⎰⎰辐射俘获截面和裂变截面之比称为俘获--裂变之比用α表示 fγσασ=有效裂变中子数 1f f a f γνσνσνησσσα===++ 有效增殖因数 eff k =+系统内中子的产生率系统内中子的总消失（吸收泄漏）率四因子公式 s deff n pf k k nεη∞ΛΛ==Λ k pf εη∞=中子的不泄露概率 Λ=+系统内中子的吸收率系统内中子的吸收率系统内中子的泄露率热中子利用系数 f =燃料吸收的热中子被吸收的热中子总数第2章-中子慢化和慢化能谱211A A α-⎛⎫= ⎪+⎝⎭在L 系中，散射中子能量分布函数 []'1(1)(1)cos 2c E E ααθ=++- 能量分布函数与散射角分布函数一一对应 (')'()c cf E E dE f d θθ→=在C 系内碰撞后中子散射角在θc 附近d θc 内的概率:2d 2(sin )sin d ()42c c r rd f d r θπθθθθθθπ===对应圆环面积球面积能量均布定律 ()(1)dE f E E dE Eα'''→=--平均对数能降 2(1)11ln 1ln 121A A A A αξαα-+⎛⎫=+=- ⎪--⎝⎭当A>10时可采用以下近似 223A ξ≈+L 系内的平均散射角余弦0μ001223c c d Aπμθθ==⎰慢化剂的慢化能力 ξ∑s 慢化比 ξ∑s /∑a 由E 0慢化到E th 所需的慢化时间t S()thE s s E E dE t v E λλξ⎤=-=-⎰热中子平均寿命为 00()11()()a d a a E t E vE v v λ===∑∑（吸收截面满足1/v 律的介质）中子的平均寿命 s d l t t =+ 慢化密度 0(,)(,)()(,)s EEq r E dE r E f E E r E dE ϕ∞''''=∑→⎰⎰(,)(,)(,)(,)(,)(1)(1)EE Eas s EE E r E r E dE E E q r E dE r E r E dE E Eααϕαϕαα''''∑-''''==∑''--⎰⎰⎰ 稳态无限介质内的中子慢化方程为 ()()()()()(Et s E E E E f E E dE S E ϕϕ∞''''∑=∑→+⎰无吸收单核素无限介质情况 ()()()()(1)Es t EE E E E dE Eαϕϕα''∑'∑='-⎰无限介质弱吸收情况dE 内被吸收的中子数 ()()()a dq q E q E dE E dE ϕ=--=∑0()exp()E a Es dE q E S E ξ'∑=-'∑⎰逃脱共振俘获概率00()()()exp()E aE s E q E dE p E S E ξ'∑==-'∑⎰第j 个共振峰的有效共振积分 ,*() ()jj AE I E E dE γσφ≡⎰逃脱共振俘获概率i p 等于 1exp A iA i i s s N I N p I ξξ⎡⎤=-=-⎢⎥∑∑⎣⎦整个共振区的有效共振积分 ()()ia EiI I E E dE σϕ∆==∑⎰热中子能谱具有麦克斯韦谱的分布形式 /1/23/22()()n E kT n N E e E kT ππ-=中子温度 ()(1)a M n M SkT T T Cξ∑=+∑ 核反应率守恒原则，热中子平均截面为()()()(()(ccc c E E E E E N E vdEE N E N E vdEN E σσσ==⎰⎰⎰⎰若吸收截面a 服从“1/v”律(a a E σσ=若吸收截面不服从“1/v ”变化，须引入一个修正因子n ga n σ=第3章-中子扩散理论菲克定律 J D φ=-∇ 3sD λ=01s tr λλμ=- 023Aμ= 001()46z s J z ϕϕ-∂=+∑∂ 001()46z s J z ϕϕ∂=∑∂＋－ 01()3z z z s J J J zφ+-∂=-=-∑∂ 33ssx y z J J i J j J k grad λλφφ=++=-=-∇中子数守恒（中子数平衡）(,)(S)(L)(A)Vdn r t dV dt =--⎰产生率泄漏率吸收率 中子连续方程 (,)(,)(,)(,)a n r t S r t r t divJ r t tϕ∂=-∑-∂如果斐克定律成立，得单能中子扩散方程 21(,)(,)(,)(,)a r t S r t D r t r t v tϕϕϕ∂=+∇-∑∂ 设中子通量密度不随时间变化，得稳态单能中子扩散方程 2()()()0a D r r S r ϕϕ∇-∑+= 直线外推距离 trd 0.7104l = 扩散长度 220011363(1)3(1)a tr a s a a s D L r λλλλμμ=====∑-∑∑-慢化长度L1 2221111112110100ln 3th a tr E D D L L E ϕϕϕϕξ∇-∑=∇-=→==∑∑∑ L 21 称为中子年龄，用τth 表示， 即为慢化长度。

核反应堆物理分析各章节重要知识点整理汇总资料第一章1、在反应堆内中子与原子的相互作用方式主要有：势散射、直接相互作用和复合核的形成。

其中复合核的形成是中子和原子相互作用的最重要方式。

2、复合核的衰变分解的方式有：共振弹性散射、共振非弹性散射、辐射俘获和核裂变，可以概括为散射和吸收。

3、共振现象：但入射中子的能量具有某些特定值，恰好使形成的复合核激发态接近于某个量子能级时，中子被靶核吸收而形成复合核的概率就显著增加，这种现象就叫作共振现象。

4、非弹性散射特点：只有当入射中子的动能高于靶核的第一激发态的能量时才能使靶核激发，也就是说，只有入射中子的能量高于某一数值时才能发生非弹性散射，由此可知，非弹性散射具有阈能的特点。

5、弹性散射特点：它可以分为共振弹性散射和势散射两种，区别在于前者经过复合核的形成过程，后者则没有。

在热中子反应堆内，对中子从高能慢化到低能的过程起主要作用的是弹性散射。

6、易裂变同位素：一些核素，如233U 、235U 、239Pu 和241Pu 等核素在各种能量的中子作用下均能发生裂变，并且在低能中子作用下发生裂变的可能性较大，通常把它们称为易裂变同位素。

7、可裂变同位素：同位素232Th 、238U 和240Pu 等只有在能量高于某一阈值的中子作用下才发生裂变，通常把它们称为可裂变同位素。

8、中子束强度I ：在单位时间内，通过垂直于中子飞行方向的单位面积的中子数量，记为I 。

9、单位体积中的原子核数N ：计算公式为AN N ρ0=0N ：阿伏加德罗常数，取值为6.0221367*1023/molρ：材料密度A ：该元素的原子量10、微观截面σ：微观截面是表示平均一个给定能量的入射中子与一个靶核发生作用的概率大小的一种度量，通常用“巴恩”（b ）作为单位，1b=10-28m 2。

11、核反应下标：s--散射；a--吸收；γ--辐射俘获；f--裂变；t--总核反应 12、靶内平行中子束强度：Nx e I x I σ-=0)(13、宏观截面∑：宏观截面是一个中子与单位体积内所有原子核发生核反应的平均概率大小的一种度量，单位为m -1,公式为：σN =∑由几种元素组成的均匀混合物质的宏观截面x ∑：∑=∑ixi i x N σ14、富集度：某种元素在其同位素中的（原子）重量百分比。

复习总结(1)主讲教师：李伟热中子反应堆中，中子反应堆中的核反应n 微观截面随能量的变化规律q 吸收截面n 低能区：大多数核素的满足1/v 律n 中能区：重核将出现强烈的共振现象q 235U的裂变截面nn 低能区：随着中子能量增加，减小n 中能区：出现共振现象n 高能区：下降到几个barn()a E s ()235583.50.0253f b eV s =()f E sc()E由裂变碎片（缓发中子先驱核）在衰变过程中释放10.71tr=S 23s =S216T Mr =A不均匀均匀反应堆的临界理论n 反射层节省q 堆芯加上反射层后，堆芯临界尺寸的减少量。

n 反射层影响1.反射层对中子吸收较弱；2.对泄漏到反射层内中子的慢化反应性的变化n 核燃料温度系数qDoppler 效应保证了核燃料温度系数为负值n 慢化剂温度系数q温度升高→慢化剂密度下降n Σa 减小→对中子的吸收减弱，f增加nΣs 减小→慢化能力减弱，p减小q 水铀比q 化学补偿毒物的影响n硼浓度过高会导致慢化剂温度系数为正设计时，水铀比应选在欠慢化区135Xe中毒135Xe产生和消失的途径nq产生：裂变直接产生，135I衰变产生q消失：发生吸收反应，自身衰变对通量(功率)变化非常敏感！135Xe 中毒n 停堆后135Xe 中毒引入的负反应性q 碘坑发生的条件：q强迫停堆11212.7610cm s --F >´×135Xe中毒n功率变化时135Xe中毒引入的负反应性浓度随时间的变化方程引入的负反应性F。

第一章—核反应堆的核物理基础直接相互作用：入射中子直接与靶核内的某个核子碰撞，使其从核里发射出来，而中子却留在了靶核内的核反应。

中子的散射：散射是使中于慢化(即使中子的动能减小)的主要核反应过程。

非弹性散射：中子首先被靶核吸收而形成处于激发态的复合核，然后靶核通过放出中子并发射γ射线而返回基态。

弹性散射：分为共振弹性散射和势散射。

微观截面：一个中子和一个靶核发生反应的几率。

宏观截面：一个中子和单位体积靶核发生反应的几率。

平均自由程：中子在介质中运动时，与原子核连续两次相互作用之间穿行的平均距离叫作平均自由程。

核反应率：每秒每单位体积内的中子与介质原子核发生作用的总次数(统计平均值)。

中子通量密度：某点处中子密度与相应的中子速度的乘积，表示单位体积内所有中子在单位时间内穿行距离的总和。

多普勒效应：由于靶核的热运动随温度的增加而增加，所以这时共振峰的宽度将随着温度的上升而增加，同时峰值也逐渐减小，这种现象称为多普勒效应或多普勒展宽。

瞬发中子和缓发中子：裂变中，99％以上的中子是在裂变的瞬间(约10-14s)发射出来的，把这些中子叫瞬发中子；裂变中子中，还有小于1％的中子是在裂变碎片衰变过程中发射出来的，把这些中子叫缓发中子。

第二章—中子慢化和慢化能谱慢化时间：裂变中子能量由裂变能慢化到热能所需要的平均时间。

扩散时间：无限介质内热中子在自产生至被俘获以前所经过的平均时间。

平均寿命：在反应堆动力学计算中往往需要用到快中子自裂变产生到慢化成为热中子，直至最后被俘获的平均时间，称为中子的平均寿命。

慢化密度：在r处每秒每单位体积内慢化到能量E以下的中子数。

分界能或缝合能：通常把某个分界能量E c以下的中子称为热中子，E c称为分界能或缝合能。

第三章—中子扩散理论中子角密度：在r处单位体积内和能量为E的单位能量间隔内，运动方向为 的单位立体角内的中子数目。

慢化长度：中子从慢化成为热中子处到被吸收为止在介质中运动所穿行的直线距离。

微观截面：一个中子和一个靶核发生反应的几率。

宏观截面：一个中子和单位体积靶核发生反应的几率。

停堆周期：全部无控制毒物都投入反应堆内时所具有的反应性。

堆芯寿期：一个新装料堆芯从开始运行到有效增殖因数降到1时，反应堆满功率运行的时间。

反应堆周期：反应堆内平均中子密度变化e倍所需的时间。

剩余反应性：堆芯没有任何控制毒物时的反应性。

瞬发临界：反应堆仅依靠瞬发中子就能达到临界的状态。

瞬发超临界：反应堆仅依靠瞬发中子就能达到超临界的状态。

多普勒效应（展宽）：共振吸收截面随温度展宽的现象。

菲克定律：中子流密度J与通量密度成正比。

控制棒微分价值：控制棒移动一步或单位距离所引起的反应性变化。

控制棒积分价值：控制棒从一参考位置移动到某一高度时，所引入的反应性。

控制棒的（反应性）价值：堆芯在有控制棒和没有控制棒时的反应性之差。

1、在热中子反应堆中为什么要使用慢化剂？慢化剂的工作原理是什么？并举出几种常用的慢化剂。

①反应堆内产生的中子能量相当高，其平均值约为2MeV；而微观裂变截面在热能区较大，热中子反应堆内的裂变反应基本上都是发生在这一能区，所以在热中子反应堆中使用慢化剂。

②在热中子反应堆中，慢化过程中弹性散射起主要作用，因为裂变中子经过与慢化剂和其他材料核的几次碰撞，中子能量便很快降低到非弹性散射的阈能一下，这是中子的慢化主要靠中子与慢化剂核的弹性散射进行。

③水、重水、石墨等。

2、缓发中子是如何产生的？在反应堆动力学分析计算中，份额不足1%的缓发中子与份额超过99%的瞬发中子相比是否可以忽略不计？为什么？①缓发中子是在裂变碎片衰变过程中发射出来的，占裂变中子的不到1%②缓发中子不可以忽略不计③缓发中子份额虽然很少，但它的发射时间较长，缓发效应大大增加了两代中子之间的平均时间间隔，从而滞缓了中子密度的变化率。

反应堆的控制实际上正是利用了缓发中子的作用才得以实现的。

3、解释碘坑现象和强迫停堆时间。

船用反应堆要求不能出现强迫停堆现象，请问在设计上应如何考虑。

1、热中子反应堆内，瞬发中子的平均寿期比自由中子的半衰期（ ）。

A、短的多；B、长的多；C、一样大。

1、某压水堆采用二氧化铀作燃料，其复集度为2.43%（重量），密度为104公斤/米2，计算：当中子能量为0.025ev时，二氧化铀的宏观吸收截面和宏观裂变截面（复集度表示铀－235在铀中所占的重量百分比）。

2、某反应堆堆芯由铀－235、水和铝组成，各元素所占的体积比分别为0.002，0.600和0.398，计算堆芯的总吸收截面（0.025ev）。

3、求热中子（0.025ev）在轻水、重水和镉中运动时，被吸收前平均遭受的散射碰撞数。

4、试比较：将2.0M电子伏的中子束减弱到1/10所需的铝、钠和铝和铅的厚度。

5、一个中子运动两个平均自由程及1/2个平均自由程而不与介质发生作用的几率分别是多少？ 6、堆芯的宏观裂变截面为5米-1，功率密度为20×106瓦/m3,求堆芯内的平均中子通量密度。

7、有一座小型核电站，电功率为15万千瓦，设电站的效率为27%，试估算该电站反应堆额定功率运行一小时所消耗的铀－235数量。

8、某反应堆在额定功率500兆瓦下运行了31天后停堆，设每次裂变产生的裂变产生的裂变产物的放射性活度为1.08×10-16t-1.2居里，此处t为裂变后的时间，单位为天，试估计停堆后24小时堆内裂变产物的居里数。

9、1）计算并画出中子能量为0.025电子伏时的复集铀的参数η与复集度的函数关系。

2）有一座热中子反应堆，无限增值系数为1.10，快中子裂变因子，逃脱共振几率和热中子利用系数三者的乘积为0.65，试确定该堆所用核燃料铀的复集度。

10、某反应堆堆芯由铀－235、水和铝组成，各元素所占的体积比分别为0.002，0.600和0.398，求堆芯的中子温度、热中子平均宏观截面和热中子利用系数。

设堆芯是均匀的，介质温度为570开， （ξσs）H2O=0.4567×10-26米2，（ξσs）Al=0.1012×10-28米2， （ξσs）U=0.126×10-28米2，堆芯的热中子能谱为麦克斯韦谱。

第1章—核反应堆物理分析中子按能量分为三类: 快中子(E ﹥0.1 MeV),中能中子(1eV ﹤E ﹤0.1 MeV),热中子(E ﹤1eV).共振弹性散射 A Z X + 01n → [A+1Z X]* → A Z X + 01n 势散射 A Z X + 01n → A Z X + 01n 辐射俘获是最常见的吸收反应.反应式为 A Z X + 01n → [A+1Z X]* → A+1Z X + γ235U 裂变反应的反应式 23592U + 01n → [23692U]* → A1Z1X + A2Z2X +ν01n微观截面 ΔI=-σIN Δx /I I IIN x N xσ-∆-∆==∆∆ 宏观截面 Σ= σN 单位体积内的原子核数 0N N Aρ=中子穿过x 长的路程未发生核反应，而在x 和 x+dx 之间发生首次核反应的概率P(x)dx= e -Σx Σdx核反应率定义为 R nv =∑ 单位是 中子∕m 3⋅s 中子通量密度nv ϕ=总的中子通量密度Φ 0()()()n E v E dE E dE ϕ∞∞Φ==⎰⎰平均宏观截面或平均截面为 ()()()EEE E dERE dEϕϕ∆∆∑∑==Φ⎰⎰辐射俘获截面和裂变截面之比称为俘获--裂变之比用α表示 fγσασ=有效裂变中子数 1f f a f γνσνσνησσσα===++ 有效增殖因数 eff k =+系统内中子的产生率系统内中子的总消失（吸收泄漏）率四因子公式 s deff n pf k k nεη∞ΛΛ==Λ k pf εη∞=中子的不泄露概率 Λ=+系统内中子的吸收率系统内中子的吸收率系统内中子的泄露率热中子利用系数 f =燃料吸收的热中子被吸收的热中子总数第2章-中子慢化和慢化能谱211A A α-⎛⎫= ⎪+⎝⎭在L 系中，散射中子能量分布函数 []'1(1)(1)cos 2c E E ααθ=++- 能量分布函数与散射角分布函数一一对应 (')'()c cf E E dE f d θθ→=在C 系内碰撞后中子散射角在θc 附近d θc 内的概率:2d 2(sin )sin d ()42c c r rd f d r θπθθθθθθπ===对应圆环面积球面积能量均布定律 ()(1)dE f E E dE Eα'''→=--平均对数能降 2(1)11ln 1ln 121A A A A αξαα-+⎛⎫=+=- ⎪--⎝⎭当A>10时可采用以下近似 223A ξ≈+L 系内的平均散射角余弦0μ001223c c d Aπμθθ==⎰慢化剂的慢化能力 ξ∑s 慢化比 ξ∑s /∑a 由E 0慢化到E th 所需的慢化时间t S()thE s s E E dE t v E λλξ⎤=-=-⎰热中子平均寿命为 00()11()()a d a a E t E vE v v λ===∑∑（吸收截面满足1/v 律的介质）中子的平均寿命 s d l t t =+ 慢化密度 0(,)(,)()(,)s EEq r E dE r E f E E r E dE ϕ∞''''=∑→⎰⎰(,)(,)(,)(,)(,)(1)(1)EE Eas s EE E r E r E dE E E q r E dE r E r E dE E Eααϕαϕαα''''∑-''''==∑''--⎰⎰⎰ 稳态无限介质内的中子慢化方程为 ()()()()()(Et s E E E E f E E dE S E ϕϕ∞''''∑=∑→+⎰无吸收单核素无限介质情况 ()()()()(1)Es t EE E E E dE Eαϕϕα''∑'∑='-⎰无限介质弱吸收情况dE 内被吸收的中子数 ()()()a dq q E q E dE E dE ϕ=--=∑0()exp()E a Es dE q E S E ξ'∑=-'∑⎰逃脱共振俘获概率00()()()exp()E aE s E q E dE p E S E ξ'∑==-'∑⎰第j 个共振峰的有效共振积分 ,*() ()jj AE I E E dE γσφ≡⎰逃脱共振俘获概率i p 等于 1exp A iA i i s s N I N p I ξξ⎡⎤=-=-⎢⎥∑∑⎣⎦整个共振区的有效共振积分 ()()ia EiI I E E dE σϕ∆==∑⎰热中子能谱具有麦克斯韦谱的分布形式 /1/23/22()()n E kT n N E e E kT ππ-=中子温度 ()(1)a M n M SkT T T Cξ∑=+∑ 核反应率守恒原则，热中子平均截面为()()()(()(ccc c E E E E E N E vdEE N E N E vdEN E σσσ==⎰⎰⎰⎰若吸收截面a 服从“1/v”律(a a E σσ=若吸收截面不服从“1/v ”变化，须引入一个修正因子n ga n σ=第3章-中子扩散理论菲克定律 J D φ=-∇ 3sD λ=01s tr λλμ=- 023Aμ= 001()46z s J z ϕϕ-∂=+∑∂ 001()46z s J z ϕϕ∂=∑∂＋－ 01()3z z z s J J J zφ+-∂=-=-∑∂ 33ssx y z J J i J j J k grad λλφφ=++=-=-∇中子数守恒（中子数平衡）(,)(S)(L)(A)Vdn r t dV dt =--⎰产生率泄漏率吸收率 中子连续方程 (,)(,)(,)(,)a n r t S r t r t divJ r t tϕ∂=-∑-∂如果斐克定律成立，得单能中子扩散方程 21(,)(,)(,)(,)a r t S r t D r t r t v tϕϕϕ∂=+∇-∑∂ 设中子通量密度不随时间变化，得稳态单能中子扩散方程 2()()()0a D r r S r ϕϕ∇-∑+= 直线外推距离 trd 0.7104l = 扩散长度 220011363(1)3(1)a tr a s a a s D L r λλλλμμ=====∑-∑∑-慢化长度L1 2221111112110100ln 3th a tr E D D L L E ϕϕϕϕξ∇-∑=∇-=→==∑∑∑ L 21 称为中子年龄，用τth 表示， 即为慢化长度。