当前位置：文档之家 › 第十四章 动量矩定理

第十四章 动量矩定理

  • 格式：ppt
  • 大小：333.00 KB
  • 文档页数：39

下载文档原格式

  / 39

合集下载

动量矩定理

动量矩定理

Lz mz (mi vi ) mi ri J z
2
定轴转动刚体对转轴的动量矩等于刚体对该轴转动惯量与角速 度的乘积。
其中，J z mi ri 2 , 称为刚体对z轴的转动惯量。
5
[例1] 滑轮A：m1，R1，R1=2R2，J1 滑轮B：m2，R2，J2 ；物体C：m3
21
证明：设质量为m的刚体，质心为C， O'z'//Cz
J zC mi ri mi ( xi yi )
2 2 2
J z ' mi ri '2 mi ( xi '2 yi '2 )
xi xi ' , yi ' yi d J z ' mi [ xi ( yi d ) 2 ]
分别代入质点系对固定点O动量矩表达式中，就有
rC mi υC rC mi υiC riC mi υiC riC mi υC rC mi υC rC mi υiC mi riC υC riC mi υiC
12
求 [例3] 已知: PA PB ; P ; r 。 。
解: 取整个系统为研究对象，
受力分析如图示。
运动分析： v =ｒ
P 将J O r 代入, 得 LO ( PA PB ) 2 g g 2 d r 2 P 由动量矩定理： [ ( PA PB )]( PA PB )r dt g 2
3 2
1 1 m1l 2 m2 (3R 2 2l 2 4lR) 3 2
23
例: 已知滑轮A的质量为m1，半径为R1，对转轴O的转动惯量为J1 ；滑轮B的

动量定理和动量矩定理

动量定理和动量矩定理
2) 如果作用于质点系的所有外力在某轴 上的投影的代数和恒等于零，则质心速度在 该轴上的投影保持不变；若开始时速度投影 等于零，则质心沿该轴的坐标保持不变。
应用质心运动定理解题步骤
1）取质点和质点系为研究对象； 2）分析质点系所受的全部外力，包括主动力和约束反力； 3）根据外力情况确定质心运动是否守恒； 4）如果外力主矢等于零，且在初始时质点系为静止，则质 心坐标保持不变。计算在两个时刻质心的坐标（用各质心 坐标表示），令其相等，即可求得所要求的质点的位移； 4）如果外力主矢不等于零，计算质心坐标，求质心的加速 度，然后应用质心运动定理求未知力。 5）在外力已知的条件下，欲求质心的运动规律，与求质点 的运动规律相同。
动力学普遍定理包括动量定理、 动量矩定理、动能定理。这些定理建 立了表现运动特征的量（动量、动量 矩、动能）和表现力作用效果的量 （冲量、冲量矩、功）之间的关系。
9.1 动量定理
1.动量 1）质点的动量
质点的质量与速度的乘积称为质点的动量， 记为mv。
动量是矢量，方向与速度方向相同。动量的单位为 N ·s。
4.质点系的动量定理
设由n个质点组成的质点系。其中第i个质点的
动 分别量为为Fmri(iiv)与i，Fr作i(e，) 用由在质该点质的点动上量的定外理力有与内力的合力
d dt
r (mivi
)

r F (e)
i

r F (i)
i
(i 1, 2,, n)
将n个方程相加，即得

d
r (mv
)

解得
y
v FOy
O
v FOx

x
C
pv
mgr A
FOx ml(a sin 2 cos) FOy mg ml(a cos 2 sin)

理论力学动量矩定理

理论力学动量矩定理

四. 平行移轴定理
刚体对某轴的转动惯量等于刚体对通过质心且与该轴平行 的轴的转动惯量，加上刚体的质量与两轴间距离的平方之乘积。
J z ' J zC m d 2
证明：设刚体的质量为m，质心为C。
O ' z '//Cz
J zC mi ri 2 mi ( xi 2 yi 2 )
J z ' mi ri ' 2 mi ( xi ' 2 yi ' 2 )
xi xi ', yi ' yi d
J z ' mi [ xi 2 ( yi d )2 ]
mi ( xi 2 yi 2 ) ( mi )d 2 2d mi yi
质点对O点的动量矩与对 z 轴的动量矩之间的关系：
M O (mv )
注意：要求 z 轴通过O点。
z
M z (mv )
二．质点系的动量矩
质点系对O点动量矩： LO 质点系对 z 轴动量矩： 同样有关系式： 例：平动刚体的动量矩。
M
O
Lz M z (mi vi )
(mv i i ) r i mv i i
( e)
PA PB d g ( d t r PA PB P / 2
）
[例4] 已知猴子A重=猴子B重，初始静止，后猴B以相对绳 速度 v 上爬，猴A相对绳不动。问猴B向上爬时，猴A将如何 动？动的速度多大？（轮重不计）
解： 设猴A向上的绝对速度为 vA，则
猴B向上的绝对速度为 vB= vvA 。
平动刚体对固定点（轴）的动量矩就等于刚体质心的动量 对该点（轴）的动量矩。

11.动量矩定理

11.动量矩定理

M
t 0 o 得D o 由
例二 . 电动绞车提升一质量为m 的物体 , 在其主动轴上作用有一个力偶其矩为 M . 已知主动轴齿轮和从动轴齿轮各自对其转轴的转动惯量分别为 J1 和 J2 . 传 动比 z2 : z1 = i ; 从动轮上的鼓轮半径为R . 不计绳索的质量和各处摩擦. 求: 重物的加速度.
v
O
解: 取整个系统为研究对象, 受力及运 动分析如图
θ
v
由对O点的动量矩定理 M d ( J O m 2 vR ) m 2 gR sin M Fy dt R ω a J O m 2 R a M m 2 gR sin R O Fx MR m 2 gR 2 sin M a J O m 2R 2 m1 g
θ
m2 g
FN
▲: 平动物体对任何一点的动量矩都很容易求得. 将若干个平动物体与一个转动物体作为一个系统 运用动量矩定理可以避免某一些未知力的出现 , 从而可简化解题的步骤.
§11 – 3 刚体绕定轴转动的微分方程
对绕定轴(不妨设为z轴)转动的刚体而言 , 对转轴的动量矩定理可 写为
n d (J zω) = ∑ M z (F i ) dt i =1
z
J z m i ri
i 1
n
mi
O
在如图示的坐标系下, 刚体对三个 坐标轴的转动惯量分别为:
y
zi
ri
Jx Jy Jz
2 2 m ( y z i i i) i 1 n 2 2 m ( x z i i i) i 1 n 2 2 m ( x y i i i) i 1
动量定理描述了物体的运动和力之间的关系,
但并不完整. 在运用动量定理时, 不能求力偶或

力学11-动量矩,动量矩定理,动量矩守恒定律

力学11-动量矩,动量矩定理,动量矩守恒定律

v
∴ ∑ miυi = 0 v
v
转动时， 转动时，
∴ ∑ miυi = 0
结论： 结论： 无论刚体静止，快转或慢转，其各质点动量之和恒为零。 无论刚体静止，快转或慢转，其各质点动量之和恒为零。 即动量已不能确切的反映刚体转动的运动状态， 即动量已不能确切的反映刚体转动的运动状态， 必须引入新的物理量——动量矩（角动量） 动量矩（ 必须引入新的物理量 动量矩 角动量）
A外 + A = mgs 内
∆Ek = 1 mυ 2 + 1 Jω 2 2 2 = 1 mR2ω 2 + 1 MR2ω 2 2 4 mgs 2 ω= 并非匀速） R 2m + M （并非匀速）
+
2mg 2 mg 1 ds dω = = β= (2m + M )R R 2m + M 2 s dt dt
L = rp = mrv
Lz = r × p = r × mv
2
Lz = rmυ = r mω = J zω
第六章 刚体力学基础 动量矩
10
质点作任何运动都可以用动量矩来描述其运动状态
例 质点对圆心的动量矩。 行星在椭圆轨道上的动量矩。 质点对圆心的动量矩。 行星在椭圆轨道上的动量矩。 v v mυ1 L v v v mυ2 ov v r2 o r1 mυ r
三. 定轴转动的动能定理 ——力矩的持续作用规律 力矩的持续作用规律
作用下，角坐标由θ 设刚体在外力矩 M 作用下，角坐标由 1→ θ2， 角速度ω1 → ω2 ， 由刚体转动定理： 角速度 由刚体转动定理：
dω M = Jβ = J dt
Mdθ = Jωdω
对于整个运动过程
∫θ
θ2

动量矩定理

动量矩定理
ma F 且 dv m F dt dv a dt
z
F
mv
o
在等式两边同时叉 乘矢径 r
r
y
x
d r (mv ) r F dt
左式：
d d dr r (mv ) r mv mv dt dt dt dr mv v mv 0 dt



其中：


－－质点系对固定点的动量矩定理 即：质点系对某固定点的动量矩对时间的导数，等于 质点系的外力对该点之矩的矢量和。
上式向轴投影后的：
dLz (e) M z(Fi ) dt
－－质点系对固定轴的动量矩定理
即：质点系对某固定轴的动量矩对时间的导数，等于 质点系的外力对该轴之矩的矢量和。
三、动量矩守恒定理
v e vc
y
vi
v i vC v ir －－－（2）
x
v
C
z
1、质点系相对固定 点运动的动量矩
o
A
vir
r
r
C
i
C
i
v e vc
y
vi
v
LO M O mi vi ri mi vi
LC M C mi vi i mi vi
x
C
－－－（3）
dx 2 m l m glsin dt
即
g sin 0 l
g sin 并令 l
2 n
——（1）
则（1）式化为
0
2 n
解此微分方程，并将运动初始条件带入，即当t=0时
0
0 0

0 cosnt

7.4 质点系对质心的动量矩定理

7.4 质点系对质心的动量矩定理

有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）
质点系对质心的动量矩定理
刚体对质心的动量矩定理 平面刚体对质心的动量矩
LC = JCω
JC
α
=
M (e) C
JC
d2 dt 2
=
M (e) C
长度为l，质量为m1的均质杆OA与半径为R，质量为m2的均质圆盘B在A处铰 接，铰链O，A均光滑。初始时，杆OA有偏角θ0 ，圆盘B有角速度ω0（逆时 针向）。求系统在重力作用下的运动规律。
解： 1. 考虑圆盘B ,受力分析。
O
根据对质心的动量矩定理
θ
B
FAy
B
FAx
A
A
ωB
m2g ωB
JCα
=
M (e) C
J BωB = 0 ωB = ω0 = const
2. 考虑杆轮系统，受力如图所示。 应用对固定点O的动量矩定理
FOy O FOx
dLO dt
n
MO (Fi(e) )
i =1
θ B
那么LC如 何求解？
有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）
质点系对质心的动量矩定理
dLO dt
= MO (Fi(e) )
dLO dt
drC dt
mvC
rC
m
dvC dt
dLC dt
rC maC
dLC dt
rC
F (e) i
dLC dt
z
z'
M
ri rC rri
质点系对质心的动量矩定理
问题的提出
dLO
dt
M O (Fi(e) )

理论力学_12.动量矩定理

理论力学_12.动量矩定理
理论力学
动量定理： 质心运动定理：
dp dt


F
(e) i
M aC

Fi
(e)
质点、质点系 动量的改变—外力（外力系主矢）
质心的运动—外力（外力系主矢） 若当质心为固定轴上一点时，vC=0，则其动量恒等于零， 质心无运动，可是质点系确受外力的作用。 动量矩定理建立了质点和质点系相对于某固定点（固轴） 的动量矩的改变与外力对同一点（轴）之矩两者之间的关系。
取固结于质心的平动参考系， 由速度合成定理，有
所以 由于 故
LC

ri m i v
i
即：质点系对质心的绝对运动动量矩，等于质点系对随质 心平动的参考系的相对运动动量矩。
结论：在计算质点系对于质心的动量矩时，用质点相对于 惯性参考系的绝对速度vi，或用质点相对于固结在质心上的 平动参考系的相对速度vi`，所得结果是一样的。 l
LO
1 P 2 g
代入 , 得
r
g
2
( P A PB
P 2
)
由动量矩定理：
d r2 P [ ( P A PB )] ( P A PB ) r dt g 2
PA PB d g dt r PA PB P /2
§8-3 动量矩守恒
动量矩定理：内力不会改变质点系的动量矩，只有外力才 能改变质点系的动量矩。 质点系的动量矩守恒 当
质点绕某心（轴）转动的问题。
二．质点系的动量矩定理 对质点Mi ：dt
d m O (m iv i ) m O ( Fi
d dt m O (m iv i )
()
) m O ( Fi
(i)
(e)

动量矩定理

动量矩定理

dLO (e) (e) mO ( Fi ) M O dt
一质点系对固定点的动量矩定理
(e) (e) (e) dLx ( e ) dL y ( e ) dL z (e) m x ( Fi ) M x , m y ( Fi ) M y , mz ( Fi ) M z dt dt dt
解：研究质点系----鼓轮与重物
M
m1g
v r
系统对O轴的动量矩：
O
Fox
v
Foy m2g
JO LO J O m2vr m2r v r
2008-7-16
24

由动量矩定理
dLo dt
M O
m1g Fox v Foy

e mo (Fi )
代入数据得：
35
§12-5
质点系相对于质心的动量矩定理 刚体平面运动微分方程
一．质点系动量矩
LO rC mvC LC r
( LC LC r )
二．质点系相对质心的动量矩定理
dLC r (e) (e) mC ( Fi ) M C dt
2008-7-16
36
三．刚体平面运动微分方程
maC F , JC mC (F )
2008-7-16 21
质点系动量矩守恒定理
质点系对于某点的动量矩守恒
2008-7-16 22
2008-7-16
23
例-2示卷扬机鼓轮质量为m1，半径为r，可绕过鼓 轮中心O的 水平轴转动。鼓轮上绕一绳，绳的一端 悬挂一质量为m2的重物。 鼓轮视为匀质，并令其对O轴的转动惯量为JO。今在鼓轮上作 用一不变力 矩M，试求重物上升的加速度。
2008-7-16 31

理论力学10动量矩定理

理论力学10动量矩定理
3D空间应用
在更高维度的空间中，动量矩定理可以通过向量的外积和叉积进行推广，适用于描述更复杂系统的动量矩变化。
n维空间推广
定理在更高维度空间的应用
多体系统
动量矩定理可以应用于多体系统，描述多个刚体之间的相互作用和运动关系，为多体动力学提供了基础。
非惯性参考系
在非惯性参考系中，动量矩定理需要考虑科里奥利力和离心力等因素的影响，以准确描述系统的动量矩变化。
定理证明的思路
在证明过程中，需要引入质点的质量、速度、位置矢量等概念，以及力、力矩等物理量。
引入相关概念
根据物理定律和数学公式，进行详细的数学推导，包括向量的点乘、叉乘等运算。
进行数学推导
经过推导，得出动量矩定理的结论，即质点系的动量矩等于外力矩对时间的积分。
得出结论Βιβλιοθήκη 定理证明的过程通过证明，得出的动量矩定理表述为：质点系的动量矩等于外力矩对时间的积分。
力矩的作用
力矩是描述力对物体运动轴的转动效应的物理量。在动量矩定理中，力矩的作用是改变物体的动量，即改变物体的运动状态。
时间和空间的影响
动量矩定理不仅涉及到物体的运动状态（动量和速度），还涉及到时间的变化率（即加速度），以及力作用的空间效应（即力矩）。因此，这个定理全面地描述了物体在空间和时间中的运动规律。
定理的物理意义
02
CHAPTER
定理的证明
首先明确动量矩定理的定义和意义，即对于一个质点系，其动量矩与外力矩之间的关系。
引入动量矩定理
建立证明框架
推导定理的表达式
根据定理的证明需求，建立证明的框架，包括定义、假设、推导和结论等部分。
根据牛顿第二定律和动量定理，推导出动量矩定理的表达式。
03

刚体定轴转动的动量矩定理和动量矩守恒

刚体定轴转动的动量矩定理和动量矩守恒

即： L0 L
mlv0 mlv Jω （1）
o
v0 m
弹性碰撞EM守恒
1 2
mv02
1 2
mv2
1 2
Jω2
（2）
其中 J 1 m' (2l)2 1 m'l 2
12
3
联立(1)、(2)式求解
v
(3m-m ')v0 m' 3m
6mv0 (m' 3m)l
o v0 m
例3 一杂技演员 M 由距水平跷板高为 h 处自由下
讨论
➢ 守 恒条件
M 0
➢ 内力矩不改变系统的动量矩.
➢ 在冲击等问题中 M in M ex L 常量
➢ 动量矩守恒定律是自然界的一个基本定律.
有许多现象都可以 用动量矩守恒来说明.
➢花样滑冰 ➢跳水运动员跳水
注意 1. 对一般的质点系统，若质点系相对于某一定点所受 的合外力矩为零时，则此质点系相对于该定点的动量 矩始终保持不变. 2. 动量矩守恒定律与动量守恒定律一样,也是自然界 的一条普遍规律.
dt 2
24 v0
7l
一、动量矩
1
质点的动量矩
质量为 m 的质点以速度
v
z
v
在O 的空位间矢运为动，r，某质时点刻相相对对于原原点
L
r
m
点的动量矩为
L
r
p
r
mv
L 的方向符合右手法则.
xo
y
L
v
r
大小 L rmvsin
一、动量矩
如质点以角速度 作半
r 径为 的圆运动，相对圆心
的动量矩:
L mr2 J
L

动量矩定理

动量矩定理

动力学的一般定理之一，它给出了粒子系统的动量矩与受到机械作用的粒子系统的冲量矩之间的关系。

动量矩定理有两种形式：微分形式和积分形式。

整体形式令粒子系统中任何粒子的质量为MI并承受外力的合力和内力加速度为0当沿着曲线移动到点Q时，速度为（见图）。

根据牛顿第二定律：将公式（1）投影到轨道的切线方向因为，通过代入等式（2），我们可以得到以下结果：。

上面的公式可以重写为：粒子I的动能在哪里？分别是粒子I的外力和内力的元素功。

对于整个粒子系统，应为：哪里是粒子系统的总动能。

通过对等式（4）进行积分，我们可以获得以下结果：其中T1是过程开始时粒子系统的动能；T2是过程结束时粒子系统的动能。

等式（5）是以积分形式表示的粒子系统的动能定理。

它表明，在某个机械过程中，粒子系统的总动能的变化等于在此过程中作用于粒子系统的所有外力和内力之和。

差异形式将公式（4）的两侧除以DT哪里是外力的力量；是内力的力量。

式（6）是粒子系统的动能定理，用微分形式表示，表明粒子系统的总动能随时间的变化率等于外力和力的总和。

单位时间内作用在粒子系统上的内力。

粒子是粒子系统的特例，因此动能定理也适用于粒子。

但是，对于粒子和刚体，由内力完成的功的总和等于零，因为前者根本不受内力的影响，而后者则成对出现，且大小相同且相反的方向，作用在同一条直线上，并且刚体的任意两个点之间的距离保持不变，因此内力完成的总功等于零。

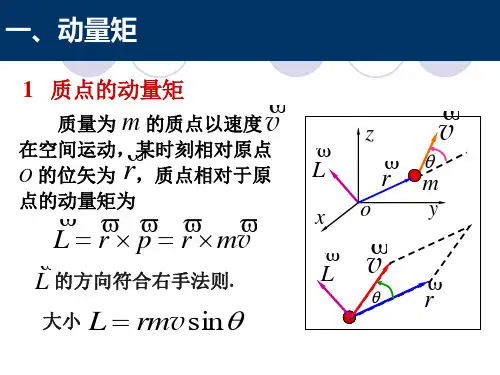
扩展数据：在机械过程的时间间隔中，粒子系统的一点动量矩的变化等于在同一时间间隔中作用在同一点上的所有外力的冲击矩的矢量和。

当刚体以角速度ω（惯性矩为iz）绕固定轴Z旋转时，可以将其投影到z轴上。

也就是说，在一定的时间间隔内，刚体在Z轴上的动量矩（izω）的变化等于作用在Z上的刚体上的所有外力的冲击矩的代数和。

同一时间间隔中的轴。

质点是质点系统的特例，因此动量矩定理也适用于质点。

动量矩和动量矩守恒定律

动量矩和动量矩守恒定律
理学院
王瑞敏
§6.3 动量矩和动量矩守恒定律
一. 动量矩 (角动量)
1. 质点的动量矩(对O点) LO r P r mv 其大小
LO rpsin mrvsin

LO
r
S
P
O
惯性参照系
特例：质点作圆周运动 例: 质点做匀速圆周运动
L rp mrv
t1
t
t2
M d t L2 L1
(质点动量矩定理的积分形式)
1
质点所受合力矩的冲量矩等于质点的动量矩的增量
西安交通大学理学院 王瑞敏
说明 (1) 冲量矩是质点动量矩变化的原因 (2) 质点动量矩的变化是力矩对时间的积累结果 2. 刚体
L J dLZ d J Z J Z M Z dt dt
跳水 芭蕾舞等
王瑞敏
猫习惯于在阳台上睡觉，因而从阳台上掉下来的事情时有发生。长期的观 察表明猫从高层楼房的阳台掉到楼外的人行道上时，受伤的程度将随高度 的增加而减少，据报导有只猫从32层楼掉下来也仅仅只有胸腔和一颗牙齿 有轻微的损伤。为什么会这样呢？ 西安交通大学理学院 王瑞敏
例 发射一宇宙飞船去考察一 质量为 M 、半径为 R 的行星， 当飞船静止于空间距行星中心 4 R 时，以速度v 0发射一 质量为 m 的仪器。要使该仪器恰好掠过行星表面 求 θ角及着陆滑行的初速度多大？ 解 引力场（有心力） 系统的机械能守恒 质点的动量矩守恒
3GM v v 0 1 2 2 Rv 0
例
一长为 l 的匀质细杆，可绕通过中心的固定水平轴在铅垂 面内自由转动，开始时杆静止于水平位置。一质量与杆相 同的昆虫以速度 v0 垂直落到距点 O l/4 处的杆上，昆虫落 下后立即向杆的端点爬行，如图所示。若要使杆以匀角速 度转动 求 昆虫沿杆爬行的速度。 解 昆虫落到杆上的过程为完全非弹性 碰撞,对于昆虫和杆构成的系统，合 l 外力矩为零，动量矩守恒 O
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

acn= 0
Y
YA
acτ= (1/2) l ε
XA C P
A
B
ω ε
X
acτ
(3)由刚体的定轴转动微分方程
J A mA ( F )
e
其中: J A 代入得:
l J A P 2 Y
YA A
1 P 2 l 3 g
3g 2 l
XA
C P
B
ω ε
X
acτ
⑷ 取坐标如图示，由质心运动定理:
⑵
P2
m2 a2 P2 T2'
⑶
由角量与线量的关系;
N r2 r1
a1 r1 a2 r2
解之
⑷ (5)
2 g (G1r1 G2 r2 ) (2G1 Q1 )r12 (2G2 Q2 )r22
1 Q1 2 Q2 2 ( r1 r2 ) T1 r1 T2 r2 ⑴ 2 g g
J m（F）
N r2 r1
W
T1 T’1 T2
P1 T’2
1 Q1 2 Q2 2 ( r1 r2 ) T1 r1 T2 r2 ⑴ 2 g g
⑷以重物为研究对象,受力分析;并由牛顿定律得:
m1a1 F1 m2 a2 F2
' m1a1 P T 1 1
' m1a1 P T 1 1
W
ቤተ መጻሕፍቲ ባይዱ
T1 T’1 T2
P1 T’2
⑵
P2
m2 a2 P2 T2'
⑶
1.5m
1.5m Q
习题14.6
O2 ⑴以轮子为研究对象,受力分析; ⑵轮子作定轴匀减速转动;末角速度为零 ⑶列转动微分方程: 解:
ω
O1
N R
F P
W
J O1 mo1 ( F )
例 图为匀质细杆0A和 CE组成；0A质量为m， CE 质量为 2 m，尺寸 如图示.求杆系对OZ轴 的转动惯量.
z
解: 分别求两杆对Z轴的 转动惯量: ⑴查表可得OA对Z轴 的转动惯量为:
Jz'=(1/3)ml2 z (2)查表，并用平行轴 定理得CE对Z轴的 转动惯量为: Jz"=(1/12)(2m)(2l)2+2ml2=(8/3)ml2 (3) 由叠加原理得杆系对Z轴的转动惯量为: Jz=Jz'+Jz"=(1/3)ml2+(8/3)ml2 = 3ml2
2 决定转动惯量的因素: ⑴刚体的质量; ⑵ 轴的位置; ⑶刚体质量的分布. (同一刚体对同一轴的转动惯量为定值)
3 刚体转动惯量的计算: ⑴质量是连续分布的，刚体对Z轴的转动惯量 Jz=∫r2dm = ∫ρ r2dv
( ρ: 密度 dv: 体积元 )
⑵质量连续均匀, ρ为常数时 Jz= ρ ∫ r2dv = (M/V) ∫r2dv ⑶几何形状规则的均匀刚体查表求Jz
dt dmz (mv ) mz (F ) dt
此式表明：质点对定轴的动量矩对时间的一 阶导数等于作用力对同一轴的矩。
my ( F )
3 质点动量矩守恒定理
⑴由质点动量矩定理知: 如果作用于质点的力对某定点O之矩恒等于 零, 质点对该点的动量矩保持常矢量。即: mo(mv) = 常矢量 ⑵由质点动量矩定理对定轴的投影式知: 如果作用于质点的力对某定轴之矩恒等于零， 质点对该轴的动量矩保持常量。
这就是刚体绕定轴转动的微分方程。 若把刚体的转动 微分方程与质点的运动微分方程的投影式加以对照． 可以看出，它们的形式完全相似，力矩与力相对应， 角加速度与加速度相对应，而转动惯量与质量相对应. 刚体的转动微分方程可以解决两类动力学问题， ①已知刚体的转动规律，求作用于刚体上的主动力
②已知作用于刚体上的主动力，求刚体的转动规律。
例1 重为P，长为 l 的、均质杆AB，其A端为 固定铰支承，B端悬挂于绳上，使杆位于水平 位置，如图所示试求当剪断绳子时AB杆的角 加速度，以及A铰链的支承反力。
解 (1)受力分析：取AB杆为研究对象， (2)运动分析，剪断绳以后，杆将作定轴转动 此瞬时杆AB转动的角速度ω＝o， 质心法向加速度 质心C点的切向加速度为
JO = (1/2)mOr2 ω= v/r
z
Yo
Xo
r
Hz = [mAr+(1/2) mOr]v
= (1/2)(2mA+mO)rv
(3) 系统受力有mAg， mog，和力偶矩M， 约束力Xo Yo(如图) (4)由质点系对z 轴的 动量矩定理得
z
Yo
Xo
r
d[(1/2)(2mA+mO)rv] / dt = M - mAgr 解方程得重物加速度为:
2(M – mAgr) a= dv/dt= 2mA+mo
习题14.2 解:
v2 r2 o r1
v1
mp F
由于质点受向心力 作用,而向心力过轴, 力矩为零,动量矩守恒 K1 = K 2
mv1 · r1 =mv2 · r2
V2=v1r1/r2=6 cm/s
习题14.5
解: ⑴以滑轮为研究对象,受力分析; ⑵滑轮作定轴转动; ⑶由刚体定轴转动微分方程:
4. 刚体定轴转动时对轴的动量矩 考虑刚体对转轴上任一点O之动量矩．建立 坐标系OXYZ．刚体绕Z 轴角速度为ω. 由质点系动量矩 定义,刚体对Z轴 的动量矩为: mivi r Lz=∑mz(mivi)
i
=∑ mivi · ri (vi =ri·ω) Lz=(∑miri2 ) · ω
Mi
4. 刚体定轴转动时 对轴的动量矩 Lz=(∑miri2 ) · ω 其中: mi 为任一质点质量, ri 为该点到Z轴距离 Jz= ∑miri2 定义为 刚体对Z轴的转动惯量 z z
4 平行轴定理
工程手册中给出的都是物体对于过质心的轴 (质心轴)的转动惯量。如果要求物体对平行于 质心轴的另一轴之转动惯量，则需利用物体 转动惯量的平行轴定理进行计算。
(已知刚体对某轴Z的 JZ,求刚体对与Z轴平行 的另一轴Z1的JZ1 z z
1
JZ1= JZ + M· h2
C点:为刚体的质心 h :为两平行轴间的距离 o
z
y
vc
解：题意分析 ， ⑴圆柱作平面运动 ⑵圆柱受力有 重力mg(巳知) 绳的张力 T(未知) ⑶质系对A点的动量矩 沿垂直于纸面的方向， 未知力T 对A之矩为零，
z
y
vc
因此可用系统对Z轴(如图示)之动量矩定理求解。
(1) 取圆柱体为研究对象．
(2) 建立坐标如图。 Az轴指向里面, 系统对Z轴的 动量矩为: z
mo(mv) = r×mv o
r
m
θ
mo(mv) = r×mv
大小: 方向: L=r· mv sin θ
V o
r θ
m 动量矩垂直于r,v决定的平面,指向由右手 螺旋法则决定 L
V θ
o
r
m
2 质点对轴的动量矩: 设有空间直角坐标系OXYZ,质量为的质点P, t时刻的速度为V ⑴定义: 质点的动量在垂直于某轴的平面上的 分量对此平面与该轴的交点O的矩.为 质点动量对该轴的动量矩. Lx = mx(mv) = mo(mvyz) = d1 ·mvyz Ly = my(mv) = mo(mvxz) = d2 ·mvxz
h
c x
y1 y
x1
例 求均匀杆对过 端点A的 Z’ 轴的 转动惯量
解:从表中查得匀质杆对质心轴z的转动惯量为 JZ=(1/12)ml2，利用平行轴定理，可得杆对过 端点A的Z'轴的转动惯量为 JZ’=(1/12)ml2 +m(l/2) 2 =(1/3)ml2
5 转动惯量的叠加原理 刚体的质量可以分成两部分(或更多部分)分别 求其对同一转轴的转动惯量,然后相加即得总的 转动惯量。
第十四章
内容提要
1
动量矩定理
首先着重讨论质点和质点系，特别是刚体的 动量矩的概念和计算;
2 接着介绍与上述有关的物理概念： 刚体的转动惯量; 3 讨论动量矩定理及其应用——刚体定轴 转动微分方程
l 4.1
动量矩的概念及其计算
1 质点对参照点的动量矩 质点的动量矩是表示质点绕某点(或某轴) 运动强弱的一种度量，它与质点的动量 mv 有关，与其点到速度矢量的距离有关。 我们把质点m在某瞬时相对于某点0 的矢 径 r 与其动量 mv 之矢量积定义为质点在该 瞬时对点 O 之动量矩。以矢量mo(mv)表示， V
Lz= mz(mv) = mo(mvxy) = d3 ·mvxy
z d1
o
z mvyz
y mvxz
d2 x
o z
y
x Lx = mx(mv) = mo(mvyz) = d1 ·mvyz Ly = my(mv) = mo(mvxz) = d2 ·mvxz Lz= mz(mv) = mo(mvxy) = d3 ·mvxy
Hz=mz(mvc)+Jc· ω =mvcr+(1/2)mr2· ω
（ ω = vc / r）
y
vc
Hz=(3/2)mrvc
(3)系统受力有mg和T 如图示，各力对AZ 轴之矩的代数和为:
z
(4)根据质点系对Z轴 的动量矩 定理得:
y
vc
ac
z 例3 图示为提升机， 已知鼓轮半径为 r , 质量为m0，可视为 匀质圆盘. 重物A 质量为mA，当鼓轮 上作用一常力偶矩 为M的力偶时，求 重物上升的加速度.
14.3动量矩定理
14.31 质点动量矩定理: 1 定理内容:
dmo (mv ) mo (F ) dt
此式表明：质点对某定点的动量矩对时间的 一阶导数，等于作用于质点的合 力对该点的矩。 这一性质称为质点动量矩定理