平面运动刚体对垂直于质量对称平面的固定轴的动量矩,等于刚体随同质心
作平动时质心的动量对该轴的动量矩与绕质心轴作转动时的动量矩之和。
15
三.质点系的动量矩定理
⒈ 质点系对固定点的动量矩定理
对质点Mi :
d dt
mO
(mi
vi
)
mO
(
Fi
(
i
)
)
mO
(
Fi
(e
)
)
(i 1,2,3,,n)
对质点系,有 ddt mO (mivi )mO (Fi(i) )mO (Fi(e) ) (i1,2,3,,n)
运动分析 v l, OM mO (mv ) 微ddt由微幅(m动分摆l 2量方动dd矩程t时)定的, 理解sinm为gdd:ltsminO,(mA sv并,in)(令dd2tmg2 Otn(2Fgl)s)ingl
mld d
dt
0
,则d 2
dt 2
l n2
ml 2 0
d
dt
代入初始条件 (t 0, 0,l0 0)
它的动量恒等于零。--
-不能用动量描述,正是
为了解决这类问题才提出 了动量矩的概念。
5
?谁最先到 达顶点
动量矩的实例一
6
?没有尾桨 的直升飞 机是怎么 飞起来的
动量矩的实例二
7
?为什么二者
转动方向相反
动量矩的实例三
8
动量矩的实例四
航天器是 怎样实现姿 态控制的
9
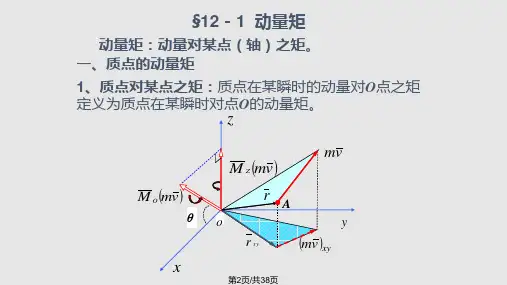
§12-1 质点的动量矩定理 1. 质点的动量矩
m aC FRe FRe 0,FRex 0,或 FRey 0,或 FRez 0
vCx = C2x,或 vCx = C2y,或 vCx = C2z