第12章 动量矩定理(田)
- 格式:doc
- 大小:191.50 KB
- 文档页数:7





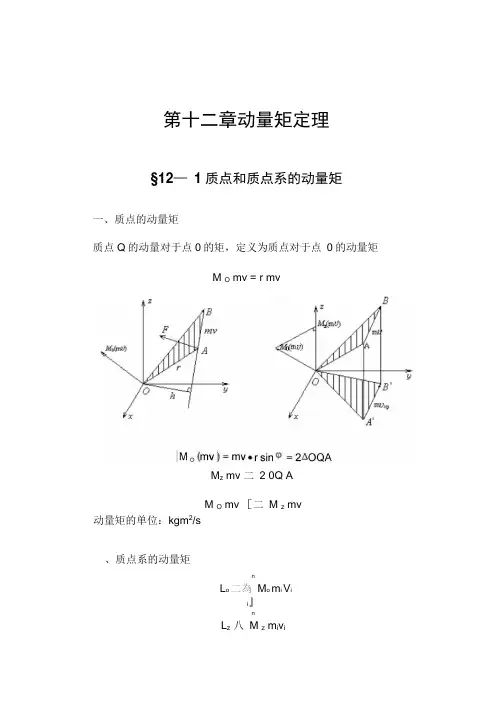
第十二章动量矩定理§12—1质点和质点系的动量矩一、质点的动量矩质点Q的动量对于点0的矩,定义为质点对于点0的动量矩M O mv = r mvM z mv 二2 0Q AM O mv [二M z mv动量矩的单位:kgm2/s、质点系的动量矩nL o 二為M o m i V ii』nL z八M z m i v iM O (mv)(r mv ) dtdtdr dtmv rmvdt绕定轴转动刚体对其转轴的动量矩等于刚体对转轴的转动惯量与转动角 速度的乘积n n n2L z 八 M z mM八 m i y 订i =mmyy ynJ z 八 m"2id :§12— 2动量矩定理、质点的动量矩定理M O mv =v mv r F dt-J—M O mv 二 M O F dt质点的动量矩定理:质点对某定点的动量矩对时间的一阶导数,等于作 用力对同一点的矩。
直角坐标投影式为d厂 一Mx(mv)= Mx(F ) dt pl 2 My(mv)=My(F ) dt plL 2M z (mv)= M z (F ) dtL z=J z :特殊情形:当质点受有心力F的作用时,如图11-4所示,力矩M°(F)=O,则质点对固定点0的动量矩M o(mv)=恒矢量,质点的动量矩守恒。
例如行星绕着恒星转,受恒星的引力作用,引力对恒星的矩M°(F)=O,行星的动量矩M o (m v )=恒矢量,此恒矢量的方向是不变的,因此行星作平面曲线运动;此恒矢量的大小是不变的,即mvh=恒量,行星的速度v与恒星到速度矢量的距离h成反比。
(1)从而由式(1)得单摆运动微分方程为护阶0(2)解式(2) 得单摆的运动规律为9 =cp o Sin( 3n t +8)其中,3-g称为单摆的角频率,单摆的周期为例1如图所示单摆,由质量为m的小球和绳索构成。
单摆悬吊于点0,绳长摆在铅垂平面内绕点0作微振幅摆动,设摆与铅垂线的夹角为「为逆时针时正,如图所示。
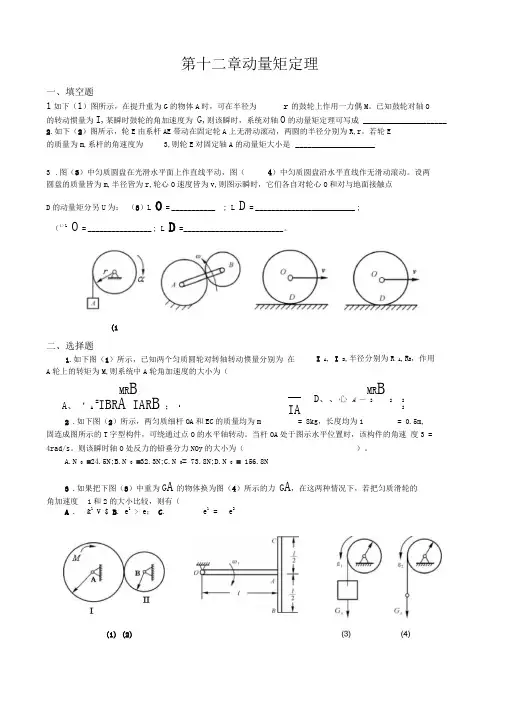
第十二章动量矩定理一、填空题1如下(1)图所示,在提升重为G 的物体A 时,可在半径为 r 的鼓轮上作用一力偶M 。
已知鼓轮对轴O 的转动惯量为I,某瞬时鼓轮的角加速度为 G,则该瞬时,系统对轴O 的动量矩定理可写成 _____________________2.如下(2)图所示,轮E 由系杆AE 带动在固定轮A 上无滑动滚动,两圆的半径分别为R,r 。
若轮E 的质量为m,系杆的角速度为3,则轮E 对固定轴A 的动量矩大小是 ____________________3 .图(3)中匀质圆盘在光滑水平面上作直线平动,图(4)中匀质圆盘沿水平直线作无滑动滚动。
设两圆盘的质量皆为m,半径皆为r,轮心O 速度皆为v,则图示瞬时,它们各自对轮心O 和对与地面接触点 D 的动量矩分另U 为: (3)L O = ___________ ; L D= _________________________ ; (4)LO = ________________ ; L D= _________________________ 。
2 .如下图(2)所示,两匀质细杆OA 和EC 的质量均为m = 8kg ,长度均为1= 0.5m, 固连成图所示的T 字型构件,可绕通过点O 的水平轴转动。
当杆OA 处于图示水平位置时,该构件的角速 度3 =4rad/s 。
则该瞬时轴O 处反力的铅垂分力NOy 的大小为()。
A.N O =24.5N;B.N O =32.3N;C.N O = 73.8N;D.N O = 156.8N 3 .如果把下图(3)中重为GA 的物体换为图(4)所示的力 G A ,在这两种情况下,若把匀质滑轮的A . &1 V $B . e 1> e ; C .e 1= e 2二、选择题1.如下图(1)所示,已知两个匀质圆轮对转轴转动惯量分别为 在A 轮上的转矩为M,则系统中A 轮角加速度的大小为(I A , I B ,半径分别为R A ,R B ,作用MRBA 、‘ A=I B R A I A R B ;BMRBI AD、、心 A —2222B A A B 角加速度 1和2的大小比较,则有((1) (2)(1三、计算题1轮子的质量m=100 kg,半径r=1 m,可以看成匀质圆盘(如图)。



第十二章 动量矩定理
一、填空题
1.如下(1)图所示,在提升重为G的物体A时,可在半径为r的鼓轮上作用一力偶M。
已知鼓轮对轴O的转动惯量为I,某瞬时鼓轮的角加速度为α,则该瞬时,系统对轴O的动量矩定理可写成______________。
2.如下(2)图所示,轮B由系杆AB带动在固定轮A上无滑动滚动,两圆的半径分别为R,r。
若轮B的质量为m,系杆的角速度为ω,则轮B对固定轴A的动量矩大小是_______________。
3.图(3)中匀质圆盘在光滑水平面上作直线平动,图(4)中匀质圆盘沿水平直线作无滑动滚动。
设两圆盘的质量皆为m,半径皆为r,轮心O速度皆为v,则图示瞬时,它们各自对轮心O和对与地面接触点D的动量矩分别为:(3)LO =___________ ;LD =_____________________; (4)LO =_____________;LD =_____________________。
二、选择题
1.如下图(1)所示,已知两个匀质圆轮对转轴转动惯量分别为I A,I B,半径分别为RA,RB,作用在A轮上的转矩为M,则系统中A轮角加速度的大小为( )。
2
2A 2
2B 2
A A
B A A 222A D
C I I M B A B
A B A B A A B B R I R I MR I M
R I R I MR +==+=+=αααα、;、;、;、 2.如下图(2)所示,两匀质细杆OA和BC的质量均为m = 8kg,长度均为l = 0.5m,
固连成图所示的T字型构件,可绕通过点O的水平轴转动。
当杆OA处于图示水平位置时,该构件的角速度ω = 4rad/s。
则该瞬时轴O处反力的铅垂分力NOy的大小为( )。
A.NO=24.5N;B.NO=32.3N;C.NO=73.8N;D.NO=156.8N
3.如果把下图(3)中重为G A 的物体换为图(4)所示的力G A ,在这两种情况下,若把匀质滑轮的角加速度ε1和ε2的大小比较,则有( )。
A . ε1 < ε;
B . ε1 > ε;
C . ε1 = ε2
(1) (2) (3)
(4)
(1) (2) (3) (4)
三、计算题
1.轮子的质量m=100 kg,半径r=1 m,可以看成匀质圆盘(如图)。
当轮子以转速n=120r/min绕定轴C转动时,在杆A点垂直地施加常力P,经过10s轮子停止。
设轮与闸块间的动摩擦系数f=0.1,试求力P的大小。
轴承摩擦和闸块的厚度都忽略不计。
答:P=270N
2.如图所示,鼓轮的质量m1=1800kg,半径r=0.25m,对转轴O的转动惯量IO=85.3kg●m2。
现在鼓轮上作用驱动转矩MO=7.43kN●m2,来提升质量m2=2700kg的物体A。
试求物体A上升的加速度,绳索的拉力以及轴承O的反力。
绳索的质量和轴承的摩擦都忽略不计。
答:(a=0.8 m/s2,T=28.6 kN,No=4 6.3 kN )
3.如图所示,物体D被装在转动惯量测定器的水平轴AB上,该轴上还固连着半径是r的鼓轮E;缠在鼓轮上细绳的下端挂着质量为M的物体C。
已知物体C被无初速地释放后,经过时间τ秒落下的距离是h;试求被测物体对转轴的转动惯量。
已知轴AB连同鼓轮对自身轴线的转动惯量是I 0。
物体D的质心在轴线
AB上,摩擦和空气阻力都忽略不计。
答:2
022Mr I h Mgr I --=τ
4.如图所示,匀质滚子质量是M,半径是r,对中心轴的回转半径是 ρ 。
滚子轴颈的半径是r 0,轴颈上绕着绳子,绳端作用着与水平面成角α的常力P,设滚子沿水平面作无滑动的滚动;试求滚子质心的加速度,以及保证滚动而不滑动的条件。
答:()(
)2
2
0cos Pr r
M r r a +-=ρα,滚而不滑条件:()
()()
2
2
2sin cos r
P Mg rr P f +-+≥
ρ
ααρ
5.如图所示,匀质杆AB长l,质量是M。
杆的一端系在绳索BD上,另一端搁在光滑水平面上。
当绳沿铅直而杆静止时杆对水平面的倾角 φ = 45°。
现在绳索突然断掉,求在刚断后的瞬时杆端A的约束反力。
( 答:Mg Mg N A 5
2
cos 212
=+=
ϕ )
6.如图所示,匀质圆柱体的质量是m,在其中部绕有细绳,绳的上端B固定不动。
现在把圆柱体由静止释放,试求下落高度h时,质心的速度、加速度以及绳索的拉力S。
(答:gh v 3
32=
,3
2g
a =
,3mg S = )
7.如图所示,管子做成半径是r的铅直圆环,对圆环直径的转动惯量是J ,以角速度ω绕定轴AC 自由
转动。
在管子内最高点A放一质量是m的小球。
由于微小扰动使小球离开点A而沿管下落,试求当小球到达点B和C时,圆环的角速度以及小球的绝对速度。
摩擦不计。
( 答:2
mr
J J B +=
ω
ω )
8.匀质杆AB和CD,质量均为m,长度都为l,垂直的固接成T字型,且D为AB杆的中点,置于铅垂平面内,该T字杆可绕光滑固定轴O转动,如图所示。
开始时系统静止,OD杆铅垂。
在一力偶M=20Mgl 的常值力偶作用下转动。
求OD杆至水平位置时,(1)OD杆角速度和角加速度;(2)支座O处的反力。
答:mg N OX 18-=;()ππ
3401792-+=mg
mg N OY
9.如图所示,跨过定滑轮D的细绳,一端缠绕在匀质圆柱体A上,另一端系在光滑水平面上的物块B上。
已知圆柱A的半径是r,质量是m1,物块B的质量m2。
试求物块B的加速度aB、圆柱质心C的加速度a
C以及绳索的拉力S。
滑轮和细绳的质量,以及轴承摩擦都忽略不计。
( 答:g m m m a B 2113+=
,g m m m m a C 212132++=,g m m m m S 2
12
13+= )
10.如图所示不可伸长的细绳绕过半径为R的定滑轮A,两端分别系与半径为r的轮子B和刚度系数为c的弹簧。
轮子A,B可看作质量分别为m1,m2的匀质圆盘,轮子B沿倾角为α的固定斜面作纯滚动,绳子与滑轮间无相对滑动。
假设在弹簧无变形时将系统由静止释放,试求轮子B中心C沿斜面下移距离s时,轮心的加速度以及斜面与轮子B间的摩擦力(绳子重量,轴承O摩擦不计)。
( 答:()2123sin 2m m cs g m a C +-=
α,()
2
1223sin m m cs g m m F +-=α )
11.如图所示,跨过定滑轮B的绳索,两端分别系在滚A的中心和物块C上。
滚子A和定滑轮B都是半径r是的匀质圆盘,各重G;物块C重G1。
滚子沿倾角是α的斜面向下作纯滚动。
绳的倾斜段与斜面平行,绳与轮B不打滑,不计绳重和轴承摩擦。
试求:(1)滚子A的质心加速度;(2)绳索AB段的拉力;(3)轴承O的反力。