八年级物理变速运动和平均速度的计算

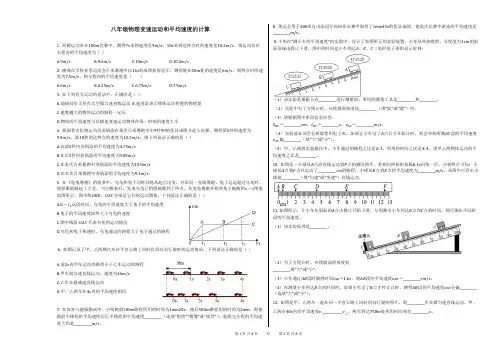
中考物理二轮考点过关：测量平均速度实验考点梳理1．变速运动与平均速度（1）变速运动的快慢就是速度变化的快慢（速度不断变化的运动，包括大小和方向），速度的变化用加速度来描述！匀变速运动呢就是速度在单位时间的增加（减少）是固定的！加速度有正负，正代表速度是增加的，负代表速度是降低的！非匀变速运动呢就是速度在单位时间内的变化不固定！（2）平均速度是指在某段时间内，物体运动的位移，与所用时间的比值，反映的是某段路程中物体运动的平均快慢．用表示平均速度，用s表示路程，用t表示时间，则平均速度的公式是＝．强化练习1．某物理兴趣小组利用如图所示的装置测量小车的平均速度。

（1）本实验是根据公式进行测量的，实验时应保持斜面的倾角（填“较大”或“较小”），这是为了减小测量（填“路程”或“时间”）时造成的误差。

（2）实验中如果得AB长度为30cm，AC长度为60cm，小车通过AB段所用时间为3s，通过AC段所用时间为5s，则小车通过上半路程的平均速度是cm/s，小车通过下半路程的平均速度是m/s，所以小车在斜面上做运动（填“匀速”或“加速”）。

2．生命在于运动，现在越来越多的人开始注重自己的锻炼，走路和跑步一般是选择最多的锻炼方式。

小明想在不借助手机软件的情况下，利用生活中的物品测量自己从家走路到小红家的平均速度。

请你帮助他设计实验方案。

（1）实验物品：。

（2）实验步骤：。

（3）实验结论：。

3．如图所示，是小璟同学做“测量小车的平均速度”的实验，实验报告（摘要）如下。

请你将其报告中的问题补充完整。

【实验目的】测量小车的平均速度【实验原理】【实验器材】小车、、停表、斜面、金属挡板、长方体木块【实验数据】如表所示测量的物理量AB段BC段AC段路程s/cm45561013.0 2.8 5.8平均速度v/（cm•s﹣1）17.4【实验分析】（1）小车全程是做（填“匀速”或“变速”）运动。

（2）实验时，为了使小车在斜面上运动的时间长些，应（填“增大”或“减小”）斜面的坡度。

2020-2021学年度人教版初中物理随堂达标真题训练——1.3运动的快慢【知识点提炼】1.物体运动的快慢用表示。

2.运动快慢的比较：①在相同时间内，物体经过的路程越，它运动得就越；②物体经过相同的路程，所花的时间越，它运动得越。

3.定义：在物理学上，把与之比叫做速度。

速度在数值上等于运动物体在时间内通过的。

4.计算公式：v=其中：s——路程——(m)；t——时间——(s)；v——速度——(m/s)5.单位：国际单位制中，速度的单位是，符号为，交通运输中常用做速度的单位，符号为，1m/s= km/h。

6.推导公式：s=，t=。

7.匀速直线运动：快慢，沿着的运动叫匀速直线运动。

匀速直线运动是最简单的机械运动。

8.平均速度：运动速度的运动叫变速运动，变速运动的快慢用来表示，粗略研究时，也可用速度的公式来计算，平均速度= 。

【真题演练】1.(2020黄石，9)甲、乙两物体，同时从同一地点出发沿直线向同一方向运动，它们的s-t 图像如图所示，下列说法正确的是（）A.0-5s内，乙的平均速度为3m/sB.3-5s内，乙做匀速直线运动C.4s时，乙在甲前方5m处D.5s时，甲、乙两物体的速度相等2.（2020潍坊，14）在操场直跑道上进行遥控小车比赛，甲、乙两车从t=0s时由同一起点同方向运动，两者运动的路程一时间图象分别如图中的甲、乙所示，下列判断正确的是（）A. 在0～5s内甲车的速度是10m/sB. 在0～5s内乙车的速度是1m/sC. t=10s时两车的速度相等D. t=10s后乙车超过甲车3.（2020株洲，1）最新研制的磁悬浮列车以600km/h的速度匀速行驶，一列高铁以300km/h 的速度匀速行驶。

与高铁相比，磁悬浮列车A.一定运动更快B.一定运动得更远C.运动时间一定更短D.可能运动更慢4.（2020菏泽，10）一辆汽车正在平直的公路上运动，用s、v和t分别表示汽车运动的路程，速度和时间下面四个图像反映汽车在做匀速直线运动的是（）A．①④B．①③C．②③D．②④5．（2020德州，15）两辆汽车在同一平直公路上同时出发，其路程s与时间t的关系如图所示。

八年级物理上册速度计算题一、简单的速度计算。

1. 一辆汽车在平直公路上行驶，通过的路程是120km，若汽车以60km/h的速度匀速行驶，求汽车行驶的时间。

- 解析：根据速度公式v = (s)/(t)，可得t=(s)/(v)。

已知s = 120km，v=60km/h，则t=(120km)/(60km/h)=2h。

2. 某人跑步的速度是5m/s，他跑了100m，求他跑步所用的时间。

- 解析：由v=(s)/(t)得t = (s)/(v)，这里s = 100m，v = 5m/s，所以t=(100m)/(5m/s)=20s。

3. 一辆摩托车以30m/s的速度匀速行驶，行驶了900m，求行驶的时间。

- 解析：根据t=(s)/(v)，s = 900m，v = 30m/s，则t=(900m)/(30m/s)=30s。

二、涉及单位换算的速度计算。

4. 一列火车的速度是72km/h，合多少m/s?- 解析：因为1km = 1000m，1h=3600s，所以72km/h=(72×1000m)/(3600s)=20m/s。

5. 一辆汽车的速度是15m/s，合多少km/h?- 解析：1m/s=(frac{1)/(1000)km}{(1)/(3600)h}=3.6km/h，所以15m/s =15×3.6km/h = 54km/h。

6. 某物体运动的速度是360m/min，合多少m/s?- 解析：因为1min = 60s，所以360m/min=(360m)/(60s)=6m/s。

三、平均速度的计算。

7. 一个人从甲地到乙地，前半程的速度是v_1 = 5m/s，后半程的速度是v_2 =3m/s，求全程的平均速度。

- 解析：设全程为2s，根据t=(s)/(v)，则前半程时间t_1=(s)/(v_1)，后半程时间t_2=(s)/(v_2)。

- 全程平均速度v=(2s)/(t_1 + t_2)，t_1=(s)/(5m/s)，t_2=(s)/(3m/s)。

初中物理教案：八年级《速度和平均速度》教学目标知识目标：1。

知道匀速直线运动速度的定义、公式。

2。

知道速度的单位“米/秒”和“千米/秒”及换算关系。

3。

变速运动和变速运动的平均速度。

能力目标：1。

思维能力：从日常生活中比较物体运动快慢来建立速度的概念，并思考比较快慢的两种方法。

2。

应用物理知识解决实际问题的能力：应用于实践，并初步了解物理计算的解题思路和规则。

情感目标：养成良好的学习习惯，规范解题步骤，养成认真细致的学习习惯。

教学建议"机械运动"教材分析教材首先通过三个问题使学生领会要比较运动的快慢必须同时考虑运动的时间和通过的路程这两个因素。

在此基础上直尺速度的定义。

在实验设计中，由学生自行提供三个玩具通过测量时间和路程计算速度，并给出了速度的公式。

教材用实际示例来建立学生一般物体运动速度的大小的观念，并给出了速度的单位，米/秒是国际主单位，而常用单位还有千米/时，并分析它们之间的换算关系。

平均速度的概念还是由实践建立的，因为实际的需求而产生的变速运动和其平均速度，平均速度的公式没有作强调，仍沿用速度的公式，只是其符号的意义发生了变化。

最后由想想议议来使学生知道一些物理量是比值物理量。

"机械运动"教法建议速度的概念，应当从一个实际问题入手，为了能区别物体的运动快慢应当如何处理，可以分学生小组讨论得出，教师总结两种方法。

快慢用物理量速度表示，进而引出了速度的概念，在此基础上用学生提供的玩具来实际测量速度，并给出了速度的公式。

速度公式也可以由学生根据实验的结论得出。

速度的单位，应当联系实际，提供大量的图片，展示不同的物体运动的一般速度，建立速度的物理图景，并提供一些视频资料，展示现代科技的发展，提高学生的学习兴趣。

关于速度单位换算，应当在长度的换算的基础上，用同样的等量代换的方法明确两个单位的换算，并让学生记住两个单位的换算关系。

平均速度，上一节内容是匀速直线运动，本节让学生思考实际情况，实际的运动都不是匀速的，但是我们需要作粗略的计算，所以引进了平均速度，最好让学生自行思考出这个思路。

匀变速直线运动中点位移的速度公式匀变速直线运动中点位移的速度公式在物理学中，匀变速直线运动是我们经常遇到的一种运动形式。

在这种运动中，物体在运动过程中的速度不断变化，但是变化的规律是确定的。

对于匀变速直线运动，我们可以通过一些公式来计算物体在某一时刻的速度。

1. 平均速度公式匀变速直线运动中，平均速度指的是物体在一段时间内所运动的总位移与总时间之比，常用符号表示为v平均。

平均速度的计算公式为：v平均= Δx / Δt其中，Δx表示物体的位移（即两个时刻之间的距离差），Δt表示时间（即两个时刻之间的时间差）。

举个例子：假设一辆汽车从初始位置出发，经过2小时后到达目的地，其初始位置与目的地之间的距离为100公里。

那么，汽车的平均速度可以通过以下公式计算：v平均= Δx / Δt = 100公里 / 2小时 = 50公里/小时因此，这辆汽车的平均速度为50公里/小时。

2. 瞬时速度公式在匀变速直线运动中，瞬时速度指的是物体在某一时刻的瞬时速率，也就是该时刻的瞬时速度。

瞬时速度的计算公式为：v瞬时 = lim(Δt→0) (Δx / Δt)其中，lim表示当Δt趋近于0时的极限值。

举个例子：假设一辆汽车在某一时刻的位移为150公里，而该时刻与前一时刻相差2小时。

利用瞬时速度公式，我们可以计算出汽车在该时刻的瞬时速度：v瞬时= lim(Δt→0) (Δx / Δt) = lim(2小时→0) (150公里 / 2小时) = lim(2小时→0) 75公里/小时 = 75公里/小时因此，在该时刻，汽车的瞬时速度为75公里/小时。

3. 加速度公式在匀变速直线运动中，加速度指的是物体在单位时间内速度的变化率。

加速度的计算公式为：a = Δv / Δt其中，Δv表示速度的变化量，Δt表示时间的变化量。

举个例子：假设一辆汽车在2小时内从初始速度50公里/小时加速到100公里/小时。

利用加速度公式，我们可以计算出汽车的加速度：a = Δv / Δt = (100公里/小时 - 50公里/小时) / 2小时 = 50公里/小时因此，在这段时间内，汽车的加速度为50公里/小时²。

两类特殊平均速度地计算公式及应用s我们知道，速度是用来表示物体运动快慢地物理量 .对于速度公式 v s ，它不 仅适用于匀速直线运动，也适用于变速运动，只不过在变速运动中，它表示物体 在通过路程 s 中地平．均．速．度．.在各类物理考试与竞赛中，常常有两类特殊地平均速 度计算问题出现 .然而由于学生对“平均速度”概念内涵理解地不准确，缺乏深入 地认识，往往导致一些“想当然”地错误 .为了加深对“平均速度”地理解与应用， 弄清知识地来龙去脉，下面就对这两类问题采用“由一般到特殊”地思维方法进 行公式推导，并对公式作简要数学分析，从中寻求规律性地结论，以便我们灵活 应用. 第 1 类问题 某物体以平均速度 v 1 行驶路程 s 1，紧接着又以平均速度 v 2 行驶路程 s 2.求该物体全程地平均速度 v 全 .b5E2RGbCAP解：∵ t1 s1 ， t2 s2v 1v 2 ss 1 s 2 s 1 s 2 (s 1 s 2 )v 1v 2 ∴ v 全 =t t 1 t 2 s 1s 2 s 2v 1 s 1v 2v 1 v 2 即 v 全=(s 1 s 2)v 1v 2 (*)s 2v 1 s 1v 2若设 m= s 1 = s1 ，n=s 2 = s2，则 0<m 、n<1 且m+n=1，于是公式( *) s s 1 s 2 s s 1 s 2 特别地，当 s 1=s 2，即 m=n=1 时，公式①变形为 v 全 = 2v1v2②2 v 1 v 2 至此，如果已知物体以不同地（平均）速度运动了两段相等地路程，用公式②计算全程地平均速度就能简化解题过程，提高解题效率 .（见例 1）p1EanqFDPw第 2 类问题 某物体在 t 1 时间内以平均速度 v 1 行驶，紧接着又在 t 2 时间内以 平均速度 v 2行驶 .求该物体全程地平均速度 v 全'.DXDiTa9E3d 变形为v 全 = v 1v 2 ① nv 1 mv 2解：∵ s 1 v 1t 1， s 2 v 2t 2's s 1 s 2v 1t 1 v 2t 2 t 1v 1 t 2v 2 ∴ v 全 = 全 t t 1 t 2 t 1 t 2 t 1t 2 即 v 全' =t1v1 t2v2 (** )t 1 t 2若设 p=t 1= t1 ，q=t 2 = t2，则 0<p 、q<1且 p+q=1，于是公式( **) t t 1 t 2 t t 1 t 2 变形为 v 全 = pv 1 qv 2 ③特别地，当 t 1=t 2，即 p=q= 1时，公式③变形为 v 全' =v 1 v 2 ④2 全 2所以，当已知物体以不同地（平均）速度在相等地时间内运动了两段不同地 路程，可以用公式④迅速计算出全程地平均速度 .（见例 2） RTCrpUDGiT从公式①②③④可以看出，上述两类平均速度地计算问题中，全程地平均速 度均与全程 s 地具体数值无关 .下面对公式①②③④作简要数学分析： 5PCzVD7HxA 若假设 0<v 1<v 2，利用数学知识，我们容易证明：1）对于公式①②③④，均有 v 1<v 全 <v 2；v 1< v 全'<v 2； ⑤ 2）对于公式②④，有 v 全 <v 全'.⑥ 证明：（1）中地结论根据“平均”地概念可以很直观地得到∴ v 全 <v 全 公式⑤⑥对于解与两类特殊平均速度有关地选择题非常有用，应用它们能对 解答进行范围估计，从而可用筛选或排除法进行选择 .（见例 1）jLBHrnAILg 公式应用举例：例 1 、小红骑车上学，当她以 4m/s 地速度骑完前一半路程时发现时间紧张， 为了不迟到，她改用 6m/s 地速度通过后一半路程，则她通过全程地平均速度是 （ ） xHAQX74J0XA 、5m/sB 、4.8m/sC 、5.2m/sD 、条件不足，无法判断分析：此题属于第 1类问题，由公式②易算得 v 全 =4.8m/s ，故选 B ；或由公式 2) ∵ v 全 - v 全 =2v 1v 2 v 1 v 2 v 1 v 2 2= (v 1 v 2) 2(v 1 v 2 )③算出 v 全' =5m/s ，又由公式⑥可知 v 全<5m/s ，而选项中只有 B 符合，故选 B.LDAYtRyKfE 例 2 、甲、乙两处相距 1．5．0．0．m ．，小李从甲地出发，前一半时间内步行，速度为1.2m/s ，后一半时间内跑步，速度为2.4m/s ，求全程地平均速度 .Zzz6ZB2Ltk 分析：此题属于第 2 类问题，用公式③可以很快计算出 v 全'=1.8m/s. 注：计算过程中，我们根本没有使用数据“ 1500m ”，因为我们知道 v 全'与全路 程 s 无关，可给可不给，属多余条件或称为干扰条件 .（思考：练习题中哪些数据 是多余条件？） dvzfvkwMI1例 3 、一人骑自行车从甲地到乙地， 全程地平均速度为 12km/h ，在前 2/3 路程 上地平均速度为 10km/h ，求后 1/3 路程上地平均速度是多少？（ 1998 年四川省初 二物理竞赛复赛试题） rqyn14ZNXI分析：此题可用公式①来计算，其中 v 全 =12km/s ，v 1=10km/h ， m=2/3，n=1/3，练习：1、汽车在平直地公路上从甲地开往乙地，它前一半时间内速度是 v 1，后一半 时间内速度是 v 2，则在全程中地平均速度为（ )SixE2yXPq5A、 v1v2 B 、 v 1 v 2 C 、 2v 1v 2 D 、 v 1 v 2v 1 v 2 2v 1 v 2 v 1v2 2、 甲、乙两地相距 s ，小车以不变地速度 v 1由甲地驶往乙地，又以更大地速 度 v 2 驶回甲地，则小车往返甲、乙两地之间地平均速度为（ ） 6ewMyirQFL3、一辆汽车从甲地驶往乙地地过程中，前一半路程内地平均速度是 30km/h ， 后一半路程内地平均速度是 60km/h ，则在全路程内汽车地平均速度为（ ） kavU42VRUs 求 v 2， 即 12=10v 2 ， 12 ， 10 v 23 3 2从而解得 v 2=20km/h.EmxvxOtOco A 、v 1 v 2 A 、 2 B 、 v 1v 2 v 1 v 2 2v 1v 2 v 1 v 2 D 、 2(v 1 v 2) v 1v 2A 、35km/h B、40km/hC、45km/hD、50km/h4、李明地家距学校600m，某天他上学时，在前3/4 时间内以1m/s 地速度走完前一段路程，为了不迟到，在后1/4 时间内，他改用 1.5m/s 地速度走完后一段路程，他上学走路地平均速度是（）y6v3ALoS89A 、1.2m/s B、1.125m/sC、2m/sD、 2.5m/s5、某滑冰运动员，滑一段斜坡，前半段地平均速度是v，后半段地平均速度是前半段地一半，则他在全斜坡滑行地平均速度是（）M2ub6vSTnP1324A 、v B、v C、v D、v34336、甲、乙两同学从跑道一端前往另一端，甲在全程时间一半内跑，另一半时间内走；乙在全程地一半路程内跑，另一半路程内时间走，如果他们走和跑地速度分别都相等，则（）0YujCfmUCwA 、甲先到终点B、乙先到终点C、同时到达终点D、无法判断7、一辆汽车在平直地公路上行驶500m，汽车通过前一半路程地平均速度为15m/s，通过后一半路程地平均速度为10m/s，则汽车在全程地平均速度是（）eUts8ZQVRdA 、12.5m/s B、20m/sC、15m/sD、12m/s8、一艘船在两地之间航行，顺水时船以速度v1 航行，逆水时船以速度v2 航行，那么一个来回船地平均速度是不是v=v1 v2?如果不是，该为多少？sQsAEJkW5T 29、从火车上下来两个旅客，他们沿同一路线走向与车站距离为S 地同一地点，甲旅客一半时间行走地速度是v1，另一半时间行走地速度是v2.而乙旅客则用速度v1走完前半程，用速度v2走完后半程.若甲、乙两旅客从车站到达同一地点所用时间分别为t1和t2，则t1=，t2=.（1998 年四川省初二物理竞赛复赛试题）GMsIasNXkA10、作变速直线运动地物体，若前一半时间内地平均速度为4m/s，后一半时间内地平均速度为8m/s，则全程地平均速度是多少？TIrRGchYzg11、甲、乙两辆汽车同时由成都开往重庆.甲车在前一半路程中地速度为v1，后一半路程中地速度为v2（v1≠ v2）；乙车在前一半时间内地速度为v1，后一半时间内地速度为v2.问：哪辆车先到达重庆？请加以证明.（第十二届全国初中物理知识竞赛初赛试题）7EqZcWLZNX通过以上分析与练习，我们认识到：无论是基本概念还是重、难、疑点，只要在平时地学习过程中，注意对概念或公式地内涵进行深入地理解，抓住概念内在地规律性，我们就能举一反三、触类旁通，提高分析问题、解决问题地能力.lzq7IGf02EKeys of exercise：s 第4 小题用公式③解；第6、9、11 小题用公式②④求解.另外第5、7 小题还可用公式④⑤⑥求解.zvpgeqJ1hk1、B2、C3、B4、B5、C6、A7、D8、不是；v= 2v1v2v1 v29、2v1v2S；v1 v2 S2v1v210、6m/s 11、甲先到达重庆；（证明参照公式⑥地证明过程）说明：第2、3、7、8 小题均可用公式②求解1、10小题用公式④解；版权申明本文部分内容，包括文字、图片、以及设计等在网上搜集整理. 版权为个人所有This article includes some parts, including text, pictures, and design. Copyright is personal ownership. NrpoJac3v1用户可将本文地内容或服务用于个人学习、研究或欣赏，以及其他非商业性或非盈利性用途，但同时应遵守著作权法及其他相关法律地规定，不得侵犯本网站及相关权利人地合法权利. 除此以外，将本文任何内容或服务用于其他用途时，须征得本人及相关权利人地书面许可，并支付报酬. 1nowfTG4KIUsers may use the contents or services of this article for personal study, research or appreciation, and other non-commercial or non-profit purposes, but at the samet ime, they shall abide by the provisions of copyright law and other relevant laws, and shall not infringe upon the legitimate rights of this website and its relevant obligees. In addition, when any content or service of this article is used for other purposes, written permission and remuneration shall be obtained from the person concerned and the relevant obligee. fjnFLDa5Zo转载或引用本文内容必须是以新闻性或资料性公共免费信息为使用目地地合理、善意引用，不得对本文内容原意进行曲解、修改，并自负版权等法律责任. tfnNhnE6e5Reproduction or quotation of the content of this article must be reasonable and good-faith citation for the use of news or informative public free information. It shall not misinterpret or modify the original intention of the content of this article, and shall bear legal liability such as copyright.HbmVN777sL。

变速运动是指物体在运动过程中速度大小或方向发生变化的运动。

而平均速度是指物体在一段时间内的位移与时间的比值，可以用来描述物体的运动速度。

本文将详细介绍变速运动和平均速度的计算方法。

一、变速运动：变速运动可以分为两种情况：匀加速运动和匀减速运动。

匀加速运动是指物体在单位时间内速度大小恒增加或减小的运动，而匀减速运动是指物体在单位时间内速度大小恒减小或增加的运动。

对于匀加速运动，我们可以使用以下公式进行计算：1.位移公式：s = ut + 1/2at²其中，s表示位移，u表示初速度，t表示运动时间，a表示加速度。

2.末速度公式：v = u + at其中，v表示末速度，u表示初速度，t表示运动时间，a表示加速度。

对于匀减速运动，我们可以使用以下公式进行计算：1.位移公式：s = ut - 1/2at²其中，s表示位移，u表示初速度，t表示运动时间，a表示减速度。

2.末速度公式：v = u - at其中，v表示末速度，u表示初速度，t表示运动时间，a表示减速度。

需要注意的是，在实际问题中，我们常常遇到的是多个阶段速度变化的情况，这时我们可以将整个变速运动的时间分成小的时间段，计算每个小时间段内速度的变化和位移的累加来求解整个变速运动的位移和时间。

二、平均速度：平均速度是指物体在一段时间内的位移与时间的比值，可以用来描述物体的运动速度。

平均速度的计算公式为：v_avg = Δs / Δt其中，v_avg表示平均速度，Δs表示位移的变化量，Δt表示时间的变化量。

需要注意的是，平均速度只能描述整个运动过程中速度的平均情况，不能反映运动过程中的速度变化细节。

如果需要研究速度的变化情况，还需要使用变速运动的计算方法进行分析。

三、实例分析：假设有一个物体以匀加速度8m/s²在直线上运动，起始时速度为6m/s，运动时间为5秒，我们来计算该物体的位移和平均速度。

1.位移计算：首先计算匀加速运动的末速度：v = u + atv=6+8*5v=46m/s然后利用位移公式计算位移：s = ut + 1/2at²s=6*5+1/2*8*5²s=30+1/2*8*25s=30+100s=130m所以，该物体的位移为130m。

两类特殊平均速度的计算公式及应用我们知道，速度是用来表示物体运动快慢的物理量。

对于速度公式ts v=，它不仅适用于匀速直线运动，也适用于变速运动，只不过在变速运动中，它表示物体在通过路程s 中的平均速度．．．．。

在各类物理考试与竞赛中，常常有两类特殊的平均速度计算问题出现。

然而由于学生对“平均速度”概念内涵理解的不准确，缺乏深入的认识，往往导致一些“想当然”的错误。

为了加深对“平均速度”的理解与应用，弄清知识的来龙去脉，下面就对这两类问题采用“由一般到特殊”的思维方法进行公式推导，并对公式作简要数学分析，从中寻求规律性的结论，以便我们灵活应用。

第1类问题 某物体以平均速度v 1行驶路程s 1，紧接着又以平均速度v 2行驶路程s 2。

求该物体全程的平均速度全v 。

解：∵ 111v s t =，222v s t =∴全v =2211212121v s v s s s t t s s ts ++=++=21122121)(v s v s v v s s ++=即全v =21122121)(v s v s v v s s ++ （*）若设m=ss 1=211s s s +，n=ss 2=212s s s +，则0<m 、n<1且m+n=1，于是公式（*）变形为全v =2121mvnv v v + ①特别地，当s 1=s 2，即m=n=21时，公式①变形为全v =21212v v v v + ②至此，如果已知物体以不同的（平均）速度运动了两段相等的路程，用公式②计算全程的平均速度就能简化解题过程，提高解题效率。

（见例1）第2类问题 某物体在t 1时间内以平均速度v 1行驶，紧接着又在t 2时间内以平均速度v 2行驶。

求该物体全程的平均速度'全v 。

解：∵ 111t v s =，222t v s =∴'全v =2122112121t t t v t v t t s s ts ++=++=212211t t v t v t ++=即'全v =212211t t v t v t ++ （**）若设p=tt 1=211t t t +，q=tt 2=212t t t +，则0<p 、q<1且p+q=1，于是公式（**）变形为全v =21qvpv + ③特别地，当t 1=t 2，即p=q=21时，公式③变形为'全v =221v v + ④所以，当已知物体以不同的（平均）速度在相等的时间内运动了两段不同的路程，可以用公式④迅速计算出全程的平均速度。