说课稿 刚体模型及其运动汇编
- 格式:ppt
- 大小:73.50 KB
- 文档页数:14

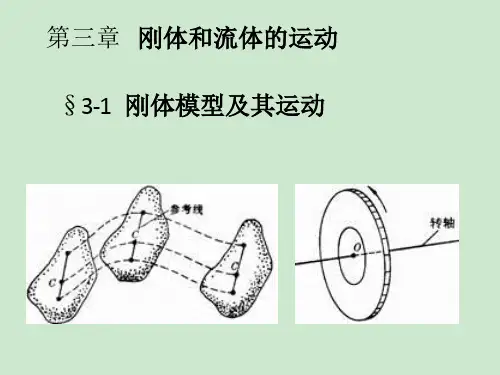
第三章刚体力学§3.1 刚体运动的分析§3.2 角速度矢量§3.3 刚体运动微分方程§3.4 刚体平衡方程§3.5 转动惯量§3.6 刚体的平动与定轴转动§3.7 刚体的平面平行运动§3.1 刚体运动的分析一、描述刚体位置的独立变量1.刚体是特殊质点组 dr ij=0,注意:它是一种理想模型,形变大小可忽略时可视为刚体。
2.描述刚体位置的独立变数描述一个质点需(x,y,z), 对刚体是否用 3n 个变量?否,由于任意质点之间的距离不变, 如确定不在同一直线上的三点,即可确定刚体的位置,需 9 个变量,由于两点间的距离保持不变,所以共需 9-3=6 个变量即可。
刚体的任意运动=质心的平动+绕质心的转动,描述质心可用(x,y,z), 描述转轴可由α, β,γ。
二、刚体的运动分类1.平动:刚体在运动过程中,刚体上任意直线始终平行.任意一点均可代表刚体的运动,通常选质心为代表.需要三个独立变量,可以看成质点力学问题.(注意:平动未必是直线运动)2.定轴转动: 刚体上有两点不动,刚体绕过这两点的直线转动,该直线为转轴. 需要一个独立变量φ3.平面平行运动: 刚体上各点均平行于某一固定平面运动。
可以用平行于固定平面的截面代表刚体。
需要三个独立变量。
4.定点运动: 刚体中一点不动,刚体绕过固定点的瞬转转动。
需三个独立的欧拉角。
5.一般运动: 平动+转动§3.2 角速度矢量定轴转动时角位移用有向线段表示,右手法确定其方向.有向线段不一定是矢量,必须满足平行四边形法则,对定点转动时,不能直接推广,因不存在固定轴.ω = lim ∆n=d n刚体在 dt 时间内转过的角位移为 d n ,则角速度定义为角速度反映刚体转动的快慢。
∆t →0 ∆t dt线速度与角速度的关系:d r =d n ⨯r , ∴ v =d rdt=ω ⨯rF 1 F ⨯ M§3.3 刚体运动微分方程一、 基础知识1.力系:作用于刚体上里的集合。



鲁科版选修2《刚体的转动及平衡》说课稿一、引言大家好,我是XX,今天我将为大家带来鲁科版选修2《刚体的转动及平衡》的说课稿。
本章主要介绍刚体的转动和平衡的基本概念及其相关定律,通过对刚体的研究,帮助学生理解刚体的运动规律,并培养学生的观察、推理和解决问题的能力。
本课将通过引导学生进行实验、展示例题、讨论分析等方式,激发学生的兴趣和思考,使他们能够灵活运用所学知识解决实际问题。
二、分析课程内容本章主要包括以下几个方面的内容:1. 刚体的基本概念在介绍刚体之前,我们先来回顾一下物体的运动。
物体的运动可以分为平动和转动两种。
平动是指物体整体沿直线运动,而转动是指物体绕某一轴旋转。
刚体是一种保持形状的物体,在运动过程中不发生形变。
2. 刚体的转动定律刚体的转动定律包括角动量守恒定律和动量定律。
角动量守恒定律指出,在没有外力作用的情况下,刚体的角动量保持不变。
动量定律是指刚体上的合外力矩等于刚体的角动量的变化率。
3. 平衡条件在介绍平衡条件之前,我们先来了解一下刚体的重心和支点。
刚体的重心是指物体的质量中心,而支点是指物体平衡时所处的点。
平衡条件包括力的平衡条件和力矩的平衡条件,力的平衡条件是指合外力等于零,力矩的平衡条件是指合外力矩等于零。
三、教学目标通过本节课的学习,学生将能够:1.理解刚体的基本概念,并能够区分平动和转动;2.掌握刚体的转动定律,包括角动量守恒定律和动量定律的应用;3.理解刚体的平衡条件,包括力的平衡条件和力矩的平衡条件;4.能够运用所学知识解决实际问题。
四、教学重点和难点本节课的教学重点是刚体的转动定律和平衡条件的理解和应用。
难点是如何将所学知识运用到实际问题的解决上。
五、教学方法和手段本课将采用以下教学方法和手段:1.实验引导:通过进行实验观察和记录,引导学生发现刚体的转动规律;2.例题展示:通过展示典型例题,引导学生理解和掌握刚体的转动和平衡;3.讨论分析:通过小组讨论和思维导图,培养学生的思考和解决问题的能力;4.视频展示:通过播放与刚体转动相关的实际视频,激发学生的兴趣;5.知识点总结:通过知识点总结和复习提高学生的学习效果。

课时安排:2课时教学目标:1. 理解刚体的概念和特性,掌握刚体运动的基本规律。
2. 熟悉刚体平动和转动的基本原理,能够运用相关公式进行计算。
3. 培养学生的物理思维能力和实验操作能力。
教学重点:1. 刚体的概念和特性2. 刚体平动和转动的基本原理3. 刚体运动的相关计算教学难点:1. 刚体运动中角动量守恒定律的应用2. 刚体转动惯量的计算教学准备:1. 教学课件2. 刚体模型3. 视频演示4. 计算器教学过程:第一课时一、导入1. 回顾高中物理中的质点运动,引出刚体概念。
2. 讲解刚体的特性:形状和大小不变,内部各点的相对位置不变。
二、刚体平动1. 介绍刚体平动的定义和特点。
2. 讲解刚体平动的基本规律:牛顿第二定律。
3. 通过实例讲解刚体平动中的受力分析和运动计算。
三、刚体转动1. 介绍刚体转动的定义和特点。
2. 讲解刚体转动的两种基本规律:转动定律和角动量定理。
3. 通过实例讲解刚体转动中的受力分析和运动计算。
四、课堂小结1. 总结刚体平动和转动的基本规律。
2. 强调刚体运动中角动量守恒定律的应用。
第二课时一、复习导入1. 回顾上节课所学内容,提问学生刚体平动和转动的基本规律。
2. 强调刚体运动中角动量守恒定律的应用。
二、刚体转动惯量1. 介绍刚体转动惯量的概念和计算方法。
2. 通过实例讲解刚体转动惯量的计算。
三、刚体运动中的角动量守恒1. 讲解刚体运动中角动量守恒定律的推导过程。
2. 通过实例讲解刚体运动中角动量守恒定律的应用。
四、课堂小结1. 总结刚体转动惯量和角动量守恒定律的应用。
2. 强调学生在实际应用中注意公式的选择和计算方法。
五、布置作业1. 完成课后习题,巩固所学知识。
2. 完成实验报告,分析实验结果。
教学反思:1. 教师应注重启发式教学,引导学生主动思考,提高学生的物理思维能力。
2. 在教学过程中,结合实际案例,帮助学生理解刚体运动的基本规律。
3. 加强实验教学,提高学生的实验操作能力。

课时:2课时教学目标:1. 让学生掌握刚体的基本概念和运动规律;2. 理解转动惯量、角速度、角加速度等物理量的含义和计算方法;3. 能够运用刚体运动定律解决实际问题。
教学重点:1. 刚体的基本概念和运动规律;2. 转动惯量、角速度、角加速度等物理量的计算。
教学难点:1. 刚体运动定律的应用;2. 转动惯量的计算。
教学准备:1. 教师准备多媒体课件、实验器材等;2. 学生准备学习笔记、计算器等。
教学过程:第一课时一、导入1. 复习高中物理中质点和质点组的运动规律;2. 引入刚体的概念,说明刚体运动的特点。
二、新课讲授1. 刚体的基本概念和运动规律:a. 刚体:形状和大小不变,且内部各点相对位置不变的物体;b. 刚体的运动分为平动和转动两种;c. 刚体的运动规律:牛顿第二定律、转动定律。
2. 转动惯量:a. 转动惯量的定义:刚体对某一转轴的转动惯量,等于刚体各质点对该转轴的转动惯量之和;b. 转动惯量的计算:刚体的转动惯量取决于刚体的质量分布和转轴的位置;c. 转动惯量的公式:$I = \sum_{i=1}^{n} m_i r_i^2$。
3. 角速度和角加速度:a. 角速度:刚体转动时,单位时间内转过的角度;b. 角加速度:刚体转动时,单位时间内角速度的变化量;c. 角速度和角加速度的计算:根据转动定律,可以计算出刚体的角速度和角加速度。
三、课堂练习1. 计算刚体的转动惯量;2. 计算刚体的角速度和角加速度。
第二课时一、复习1. 复习第一课时所学内容,重点掌握刚体的基本概念和运动规律;2. 解答学生提出的问题。
二、新课讲授1. 刚体运动定律的应用:a. 牛顿第二定律在刚体运动中的应用;b. 转动定律在刚体运动中的应用;c. 刚体运动问题的解题方法。
2. 实例分析:a. 计算刚体绕定轴转动的角速度和角加速度;b. 计算刚体绕定轴转动的转动动能;c. 分析刚体在复杂受力下的运动情况。
三、课堂练习1. 解答刚体运动问题;2. 分析刚体在复杂受力下的运动情况。




刚体的运动和转动刚体是指物体在运动或转动过程中,各部分之间保持相对位置不变的物体。
在物理学中,刚体是一个重要的概念,它的运动和转动具有一定的规律和性质。
本文将详细探讨刚体的运动和转动,以及相关的基本概念和原理。
一、刚体的运动刚体的运动是指整个物体的平动,即物体作为一个整体的运动。
平动可以是沿直线运动,也可以是曲线运动。
根据牛顿第一定律,当物体所受合外力的矢量和为零时,物体将保持静止或匀速直线运动。
而当物体所受合外力的矢量和不为零时,物体将发生加速度,即产生直线运动。
刚体的平动可以通过理解质点来进行分析。
质点是指物体的质量集中在一个点上,没有形状和大小,无论是刚体还是非刚体,都可以看作是由许多质点组成的。
因此,在分析刚体的平动时,可以把刚体简化为质点。
同时,刚体的平动也满足牛顿第二定律,即合外力等于质量乘以加速度。
二、刚体的转动刚体的转动是指物体绕某个轴进行旋转的运动。
转动的轴可以是任意选择的,但通常选择物体上的某个固定点或固定轴线作为转动的轴。
在刚体的转动中,每一个点都绕轴线进行圆周运动,并且所有点的转动角度相等。
刚体的转动可以由物体的转动惯量和转动力矩来描述。
转动惯量是物体对转动的抵抗程度或者旋转惯性的量度,它与物体的质量分布和形状密切相关。
转动力矩则是引起刚体转动的力和力臂的乘积,它的方向由右手定则给出。
根据角动量守恒定律,当刚体不受外力矩作用时,刚体的角动量守恒。
这意味着刚体的角动量大小和方向在运动过程中保持不变,从而导致刚体产生转动。
三、刚体的动力学方程刚体的运动和转动都可以通过动力学方程来描述。
对于平动的刚体,动力学方程可以表示为:∑F = ma其中,∑F表示物体所受合外力的矢量和,m表示物体的质量,a表示物体的加速度。
而对于转动的刚体,动力学方程可以表示为:∑τ = Iα其中,∑τ表示物体所受合外力矩的矢量和,I表示刚体的转动惯量,α表示刚体的角加速度。
四、刚体的运动和转动的实例刚体的运动和转动在日常生活和工程领域中有着广泛的应用。
第四章 刚体的转动§4-1刚体运动一、刚体定义:物体内任意二点距离不变的物体称为刚体。
说明:⑴刚体是理想模型⑵刚体模型是为简化问题引进的。
二、刚体运动刚体运动:(1)平动:刚体内任一直线方位不变。
特点:各点运动状态一样,如:a 、v 等都相同,故可用一个点来代表刚体运动。
(2)转动:1)绕点转动2)绕轴转动:刚体中所有点都绕一直线作圆周运动说明:刚体的任何运动都可看作平动与转动的合成。
(如:乒乓球飞行等) 三、定轴转动(本章仅讨论此情况)定义:转轴固定时称为定轴转动。
转动特点:⑴刚体上各点的角位移θ∆相同(如:皮带轮),各点的ω、α相同。
⑵刚体上各点的)(ωr v =、)(2ωr a n =、 ()αr a t =一般情况下不同。
说明:⑴ω是矢量,方向可由右手螺旋法则确定。
见图4-1。
⑵r v ⨯=ω图 4-1§4-2 力矩 转动定律 转动惯量一、力矩1、外力F在垂直于轴的平面内 如图4-2: 定义:⑴力矩: F r M⨯= (4-1)⑵力矩 :大小:θsin Fr Fd M ==(θsin r d =,称为力臂);方向:沿(F r⨯它垂直于r 、F构成的平面即M 与轴平行。
注意:θ是r、F 间夹角。
2、外力F不在垂直于轴的平面内如图4-3: (垂直轴)平行轴)⊥+=F F F(// ∵ //F对转动无贡献∴ 对转动有贡献的仅是⊥F。
F 产生的力矩即⊥F的力矩,故上面的结果仍适用。
说明:F平行轴或经过轴时0=M 。
二、转动定律0≠M 时,转动状态改变,即0≠α ,那么α与M的关系如何?这就是转动定律的内容。
推导:如图4-4,把刚体看成由许多质点组成的系统, 这些质点在垂直于轴的平面内作圆周运动。
考虑第i 个质点: 质量:i m ∆到轴的距离:i r受力:外力:i F;内力:i f (设i F、i f在垂直于转轴的平面内) 在切线方向上由牛顿定律有:αi i t i it it r m a m f F ∆=∆=+ (4-2)图 4-3⊥F 图 4-4即 αθϕi i i i i i r m f F ∆=+sin sin (4-3) (4-3)×i r : αθϕ2sin sin i i i i i i i i r m r f r F ∆=+⇒ (4-4) 每一个质点都有一个这样方程,所有质点对应方程求和之后,有αθϕ⎥⎦⎤⎢⎣⎡∆=+∑∑∑i i i i i i i i i i i r m r f r F 2sin sin (4-5)可证明0sin =∑iii i r F θ合内力矩。