下载文档原格式
第7.5节 刚体平面运动的动力学7.5.1 10m 搞得烟筒因底部损坏而倒下来，求其上端到达地面时的线速度。
设倾倒时底部未移动。
可近似认为烟筒为均质杆。
解：烟筒的长度l =10m 。
设烟筒上端到达地面的瞬间，烟筒绕其底部的转动角速度为ω。
在倾倒过程中，只受重力作用，做的功为：mg ⋅½l 。
由刚体定轴转动的动能定理：lgmlI I l mg 323122121=∴==⋅ωω烟筒上端到达地面时的线速度为：s m gl l v /2.17108.933≈⨯⨯===ω7.5.2 用四根质量各为m 长度各为l 的均质细杆制成正方形框架，可围绕其中一边的中点在竖直平面内转动，支点O 是光滑的．最初，框架处于静止且AB 边沿竖直方向，释放后向下摆动，求当AB 边达到水平时，框架质心的线速度C v。
以及框架作用于支点的压力N ．解：先求正方形框架对通过其质心且与其垂直的转轴（质心轴）的转动惯量：框架的质心位于框架的中心，即两条对角线的交点上。
每根细杆对其本身的质心轴的转动惯量：21210ml I =，细杆的质心与框架的质心的距离为l 21，由平行轴定理：2342210])([4ml l m I I c =⋅+⋅=再由平行轴定理，得框架对通过0点的转轴的转动惯量：237221)(4ml l m I I c =⋅+=(1)求框架质心的线速度v c框架在下摆过程中，只有重力做功，机械能守恒。
选取杆AB 达到水平时框架质心位置位势能零点，得：gll v l h m M I Mgh c lgc c 7321712212214===∴===ωωω（2）求框架对支点的压力N以框架为研究对象，它受到重力M g 和支点的支撑力N 的作用，由质心运动定理：c a M g M N =+取自然坐标系，τ沿水平方向，n 铅直向上，得投影方程：βτττc n c c n n Mh Ma N mgmg mg N mg l gl m h v M Ma Mg N n===+=⇒=⋅===-7372472421732744:ˆ:ˆ在铅直位置时，外力矩为0，故角加速度β=0，==〉N τ = 07.5.3 由长为l ，质量各为m 的均质细杆组成正方形框架，其中一角连于光滑水平转轴O ，转轴与框架所在平面垂直．最初，对角线OP 处于水平，然后从静止开始向下自由摆动．求OP 对角线与水平成450时P 点的速度，并求此时框架对支点的作用力．解：先求正方形框架对通过其质心且与其垂直的转轴（质心轴）的转动惯量：框架的质心位于框架的中心，即两条对角线的交点上。
刚体平面运动微分方程
一般来说，物体运动过程中都受到各种力的作用，此外，如果是连续体，由于运动而产生的声学变化也都会影响运动状态，因此就需要研究物体运动中力和声学变化之间的关系。
在力学分析中，相对论块集体动力学（Classical Dynamics）是最基本的物理系统，它描述了物体运动的微分方程，从而可以求出物体的运动状态。
平面运动动力学是指物体运动过程中的动力学分析，可以用来描述物体在平面上的运动状态，包括具体的位置、速度、加速度等。
可以使用牛顿第二定律将机械力和物体加速度联系起来，写成机械力和物体加速度的微分方程，它的形式为：
F=m·a，
其中F表示机械力，m表示物体的质量，a表示物体的加速度。
物体在平面上的运动还会受到一些拖拽力的影响，比如阻力和空气阻力等，如果将拖拽力也考虑在内，则可以将上述方程修正为：
其中b表示拖拽力，v表示物体运动状态时的速度。
此外，如果物体处于受到旋转力作用的情况下，则可以将其表述为：
F=m·a+b·v+c·(ω×r)，
其中c表示旋转抗力，ω表示旋转角速度，r表示物体圆心到物体某一点的距离。
由此可以得到物体平面运动的微分方程：
其中Δp表示物体加速度变化，F表示物体受到机械及其拖拽力和旋转抗力的作用。
从而可以根据上述微分方程，求出物体在平面上运动过程中的状态和性质，从而又可以了解物体在机械及其拖拽力和旋转抗力作用下，在平面上的运行状态。
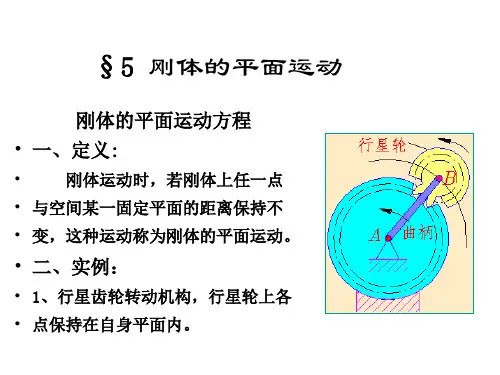
刚体的平面运动-运动分解刚体的平面运动刚体在运动过程中，其上任意一点到某一固定平面的距离保持不变。
M NS A 1A 2 A若用一与固定平面M 平行的平面N 去截割刚体得平面图形S ， 该平面图形S 始终在平面N 内运动。
垂直于图形S 的任一条直线A 1A 2作平动。
刚体的平面运动可以简化为平面图形S 在其自身平面内的运动。
研究刚体的平面运动 研究平面图形的运动12()()A A x f t y f t ==刚体平面运动方程点A 、B 是平面图形上的任意两点，AB 位置确定，平面图形的位置也唯一确定。
3()f t φ= 由刚体的平面运动方程可以看到，如果图形中的A 点固定不动，则刚体将作定轴转动；如果线段AB 的方位不变（即ϕ =常数），则刚体将作平动。
用什么方法研究刚体的平面运动？如果汽车沿直线行驶，车轮作平面运动。
建立动参考系x’o’y’,随车身一起平动。
轮相对轮心做转动刚体的平面运动分解为随平动参考系的平动（牵连运动）与绕基点的“定轴”转动（相对运动）。
SA ϕ x ' y ' O ' ϕ' 刚体的平面运动(绝对运动)随同基点的平动(牵连运动) 绕着基点的转动(相对运动) 刚体的平面运动分解与合成xy o S Aϕx ' y 'O ' 有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）∆r A ≠ ∆r B ， v A ≠ v B ， a A ≠ a B—随基点的平动部分与基点的选择有关△ϕ1=△ϕ2=△ϕωA = ω B = ωαA = α B = α—绕基点的转动部分与基点的选择无关基点选择对运动分析有何影响？凡涉及到平面运动图形转动的角速度和角加速度时，不必强调基点，就是平面图形的绝对角速度和角加速度。
O ABθ ϕSA ϕ x ' y ' O ' ϕ' 刚体的平面运动(绝对运动)随同基点的平动(牵连运动) 绕着基点的转动(相对运动) 刚体的平面运动分解与合成xy o S Aϕx ' y 'O '思考题刚体的平动和定轴转动均是刚体平面运动的特例，对吗？有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）。
力学（第二版）漆安慎习题解答第七章刚体力学第七章 刚体力学 一、基本知识小结⒈刚体的质心定义：∑⎰⎰==dm dm r r mr m r c i i c //求质心方法：对称分析法，分割法，积分法。
⒉刚体对轴的转动惯量定义：∑⎰==dm r I r m I ii 22平行轴定理 I o = I c +md 2 正交轴定理 I z = I x +I y.常见刚体的转动惯量：（略） ⒊刚体的动量和质心运动定理∑==c c a m F v m p⒋刚体对轴的角动量和转动定理∑==βτωI I L⒌刚体的转动动能和重力势能c p k mgy E I E ==221ω⒍刚体的平面运动=随质心坐标系的平动+绕质心坐标系的转动动力学方程：∑∑==c c c c I a m F βτ（不必考虑惯性力矩）动能：221221cc c k I mv E ω+= ⒎刚体的平衡方程∑=0F， 对任意轴∑=0τ二、思考题解答7.1 火车在拐弯时所作的运动是不是平动？答：刚体作平动时固联其上的任一一条直线，在各时刻的位置（方位）始终彼此平行。
若将火车的车厢看作一个刚体，当火车作直线运行时，车厢上各部分具有平行运动的轨迹、相同的运动速度和加速度，选取车厢上的任一点都可代替车厢整体的运动，这就是火车的平动。
但当火车拐弯时，车厢上各部分的速度和加速度都不相同，即固联在刚体上任一条直线，在各时刻的位置不能保持彼此平行，所以火车拐弯时的运动不是平动。
7.2 对静止的刚体施以外力作用，如果合外力为零，刚体会不会运动？答：对静止的刚体施以外力作用，当合外力为了零，即0i c F ma ==∑时，刚体的质心将保持静止，但合外力为零并不表明所有的外力都作用于刚体的同一点。
所以，对某一确定点刚体所受合外力的力矩i i iM M r F ==⨯∑∑不一定为零。
由刚体的转动定律M J α=可知，刚体将发生转动。
比如，置于光滑水平面上的匀质杆，对其两端施以大小相同、方向相反，沿水平面且垂直于杆的两个作用力时，杆所受的外力的合力为零，其质心虽然保持静止，但由于所受合外力矩不为零，将作绕质心轴的转动。
常见刚体运动的动力学分析方法刚体是指在运动过程中保持形状不变的物体，它的运动可以通过动力学分析方法来研究。
本文将介绍常见的刚体运动的动力学分析方法。
一、平面刚体运动的动力学分析方法在平面刚体运动中，刚体在平面上的运动可以分解为质心运动和绕质心的旋转运动。
常见的动力学分析方法包括线动量定理、角动量定理和动能定理。
1. 线动量定理线动量定理描述了刚体在平面上的线动量变化与合外力矩之间的关系。
根据线动量定理，刚体在一个时间间隔内的线动量变化等于作用在刚体上的合外力矩乘上时间间隔。
线动量定理的数学表达式为：Δp= ∑F⃗ ×Δt，其中Δp表示线动量的变化量，F⃗表示合外力矩，Δt表示时间间隔。
2. 角动量定理角动量定理描述了刚体在平面上围绕质心旋转时的角动量变化与合外力矩之间的关系。
根据角动量定理，刚体在一个时间间隔内的角动量变化等于作用在刚体上的合外力矩乘上时间间隔。
角动量定理的数学表达式为：ΔL = ∑τ⃗ ×Δt，其中ΔL表示角动量的变化量，τ⃗表示合外力矩，Δt表示时间间隔。
3. 动能定理动能定理描述了刚体在平面上的动能变化与合外力矩之间的关系。
根据动能定理，刚体在一个时间间隔内的动能变化等于作用在刚体上的合外力矩与刚体的质量乘积乘上时间间隔。
动能定理的数学表达式为：ΔE = ∑τ⃗ ×Δθ，其中ΔE表示动能的变化量，τ⃗表示合外力矩，Δθ表示角位移。
二、空间刚体运动的动力学分析方法在空间刚体运动中，刚体在三维空间上的运动可以分解为质心运动和绕质心的旋转运动。
常见的动力学分析方法包括动量矩定理、角动量矩定理和动能定理。
1. 动量矩定理动量矩定理描述了刚体在空间上的动量矩变化与合外力和合外力矩之间的关系。
根据动量矩定理，刚体在一个时间间隔内的动量矩变化等于作用在刚体上的合外力和合外力矩乘上时间间隔。
动量矩定理的数学表达式为：ΔL = ∑M⃗ ×Δt，其中ΔL表示动量矩的变化量，M⃗表示合外力矩，Δt表示时间间隔。
