下载文档原格式
圆锥的侧面展开图问题解决圆锥问题的关键是明确圆锥的侧面展开图各元素与圆锥各元素的关系——圆锥的侧面展开图是扇形，扇形的半径是圆锥的母线，弧长是圆锥的底面圆的周长．问题往往涉及圆锥的母线长、圆锥的高以及底面半径之间的关系，勾股定理则是架起三元素间的桥梁．如图1，设圆锥的底面半径为r ，母线AB 的长为l ，高为h ，则r 2+h 2=l 2，圆锥的侧面展开图是扇形ACD ，该扇形的半径为l ，设扇形ACD 的圆心角是θ，则扇形的弧CD 的长=2πr =180l θπ，圆锥的侧面积为S 侧=12×2πr ×l =πrl ．一、计算圆锥的侧面积例1 （邵阳）如图2所示的圆锥主视图是一个等边三角形，边长为2，则这外圆锥的侧面积为______（结果保留π）．分析：依题意，圆锥主视图是一个等边三角形，所以圆锥的母线长为2，底面半径为1，可以直接代入公式求得．解：依题意，r=1，l =2，所以S 侧=π×1×2=2π．二、求圆锥的母线长例2 （桂林）已知圆锥的侧面积为8πcm 2, 侧面展开图的圆心角为45°，则该圆锥的母线长为（ ）．（A ）64cm （B ）8cm （C ）22cm （D ）2cm 分析：圆锥的侧面积即其侧面展开图扇形的面积，由扇形的面积公式可求出圆锥的母线长（侧面展开图扇形的半径即为圆锥的母线长）．解：由2360n l S π=扇形，即2360n l π＝8π，解得l ＝8（cm ）．故应选（B ）． 三、计算圆锥的底面半径例3 （日照）将直径为60cm 的圆形铁皮，做成三个相同的圆锥容器的侧面（不浪费材料，不计接缝处的材料损耗），那么每个圆锥容器的底面半径为（ ）．（A ）10cm （B ）30cm （C ）40cm （D ）300cm分析：依题意，将直径为60cm 的圆形铁皮分割成三个大小相等的扇形，这三个扇形即三个相同的圆锥容器的侧面展开图．根据“侧面展开图扇形的弧长是圆锥的底面圆的周长”可求每个圆锥容器的底面半径．解：直径为60cm 的圆形铁皮的周长为60πcm ，故将该铁皮分割成三个大小相等的扇形的弧长为20πcm ．图1 图2设圆锥的底面半径为r ，则2πr ＝20π，解得r ＝10．故应选（A ）．四、计算圆锥的高例4 （鸡西）如图3，小明想用图中所示的扇形纸片围成一个圆锥，已知扇形的半径为5cm ，弧长是6πcm ，那么围成的圆锥的高度是 cm ． 分析：借助图1分析，知在r 2+h 2=l 2中，欲求h ，需知道r ，l ，显然这里l ＝5 cm ，故只需再求出r ．解：设圆锥的底面半径为r ，则2πr ＝6π，解得r ＝3．所以h 2=l 2－ r 2＝52－32，所以h ＝4（cm ）．五、计算侧面展开图中扇形圆心角的度数 例5 （成都）若一个圆锥的底面圆的周长是4πcm ，母线长是6cm ，则该圆锥的侧面展开图的圆心角的度数是（ ）．（A ）40° （B ）80° （C ）120° （D ）150°分析：设圆锥展开图的圆心角为n °，根据弧长公式可求出侧面展开图扇形的弧长为180n l π，再根据“侧面展开图扇形的弧长是圆锥的底面圆的周长”列方程可解． 解：设圆锥展开图的圆心角为n °，则4π=6180n πg ． 解得n ＝120．所以选（C ）．六、最短路径问题例6 （青岛）如图4是一个用来盛爆米花的圆锥形纸杯，纸杯开口圆的直径EF 长为10cm ．母线OE （OF ）长为10cm ．在母线OF 上的点A 处有一块爆米花残渣，且FA ＝2cm ，一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点．则此蚂蚁爬行的最短距离为 cm ．分析：由于小蚂蚁只能在圆锥侧面上爬行，所以我们可考虑把圆锥侧面展开，将问题转化为平面图形解决.将圆锥沿母线OE 剪开，如图7所示的展开图，根据“两点之间线段最短”，知EA 即为最短路径．解：设圆锥侧面展开后扇形的圆心角为n °，因为底面的周长等于展开后扇形的弧长，所以180n OE π⋅＝π E F ，即10180n π⋅＝10π，解得n °＝180°． 此圆锥的侧面展开图为扇形（如图5），在Rt △AEO 中， OA ＝OF －AF ＝8（cm ），O B A 图3 5cm 图5 Ａ Ｆ Ｅ Ｏ 图4。
2023圆弧长和扇形的面积圆锥的侧面展开图CATALOGUE 目录•圆弧长和扇形的面积•圆锥的侧面展开图•从圆弧长和扇形的面积看圆锥的侧面展开图01圆弧长和扇形的面积圆弧长的正投影长度等于圆心角的大小根据圆的周长公式 C=2πr，圆弧长的公式为 L=C/θ，其中θ为圆心角的大小若已知圆弧所在圆的半径为r，则圆弧长的计算公式为 L=θr扇形的面积是指扇形所占圆心角大小和半径平方的比值若已知扇形的半径为r，圆心角的大小为θ，则扇形的面积计算公式为 S=1/2θr^2若已知扇形的半径为r，则扇形的面积计算公式为S=πr^2/360°•圆弧长和扇形的面积有着密切的联系，若已知扇形的半径为r，圆心角的大小为θ，则扇形的面积与圆弧长的关系为 S=1/2θr^2=1/2Lr，其中L为圆弧长圆弧长和扇形面积的关系02圆锥的侧面展开图圆锥的侧面展开图是扇形圆锥的侧面展开图由一个圆心角和弧长组成圆心角是扇形的角度，弧长是扇形的半径圆锥的侧面展开图定义圆锥的侧面展开图的画法确定圆锥的母线和圆心角画出扇形的弧长标注出扇形的角度和弧长计算圆锥的表面积求圆锥的侧面积圆锥的侧面展开图的应用03从圆弧长和扇形的面积看圆锥的侧面展开图圆锥侧面展开图是扇形，其圆弧长度等于圆锥底面圆的周长。
扇形的半径等于圆锥母线长，扇形的圆心角等于圆锥底面圆的圆心角。
圆锥的侧面展开图与圆弧长的关系圆锥侧面展开图面积等于扇形面积，即 S=1/2 × 圆弧长 × 半径。
当圆锥母线长和底面圆半径确定时，圆锥侧面展开图面积与底面圆周长成正比。
圆锥的侧面展开图与扇形面积的关系圆锥的侧面展开图的应用实例展示制作圆锥通过圆锥的侧面展开图，可以制作圆锥，只需要将扇形分成若干份，然后按照顺序折叠即可。
计算圆锥体积和表面积通过圆锥的侧面展开图，可以计算出圆锥的表面积和体积，只需要将扇形面积相加即可。
设计旋转体通过圆锥的侧面展开图，可以设计旋转体，只需要将扇形分成若干份，然后按照顺序旋转即可。
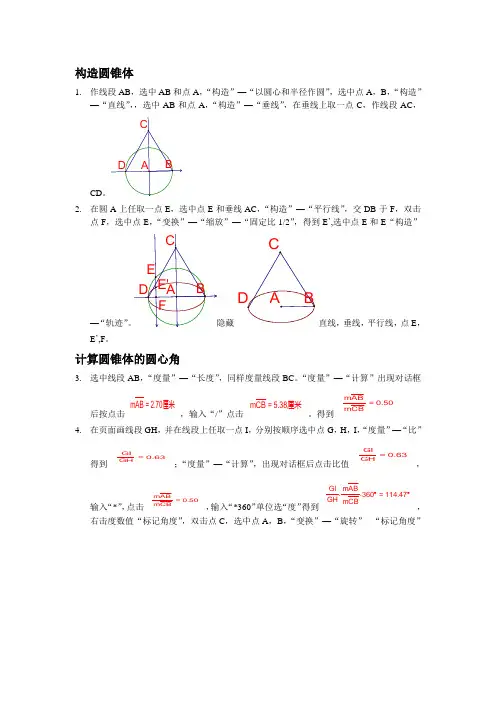
—“以圆心和半径作圆”，选中点A ，B ，“构造”—“垂线”，在垂线上取一点C ，作线段AC ，AC ，“构造”—“平行线”，交DB 于F ，双击—“固定比1/2”，得到E ’,选中点E 和E “构造”直线，垂线，平行线，点E ，E ’,F 。
计算圆锥体的圆心角3. 选中线段AB ，“度量”—“长度”，同样度量线段BC 。
“度量”—“计算”出现对话框后按点击mAB = 2.70厘米，输入“/”点击mCB = 5.38厘米。
得到4. 在页面画线段GH ，并在线段上任取一点I ，分别按顺序选中点G ，H ，I ，“度量”—“比”得到GIGH= 0.63；“度量”—“计算”，出现对话框后点击比值GIGH= 0.63，输入“*”，点击mAB，输入“*360”单位选“度”得到GI GH ⋅360︒ = 114.47︒，右击度数值“标记角度”，双击点C ，选中点A ，B ，“变换”—“旋转”--“标记角度”得到点A’,B’。
GH⋅360︒ = 114.47︒GIGH= 0.63mCB = 4.27厘米mAB = 2.14厘米B'A'G HI“度量”—“计算”出现对话框后点击GIGH= 0.63输入“*365.98”单位“度”输入“-359.99”单位“度”得到GI GH ⋅359.98︒-359.99︒ = -131.75︒。
右击GIGH⋅359.98︒-359.99︒ = -131.75︒“标记角度”。
双击点A’，选中点B’“变换”—“旋转”—“标记角度”得到点B’’。
构造轨迹5.分别按顺序选中A’,B’’,B’,“构造”—“圆上的弧”。
作直线A’B’,在弧上任取一点P，过点P作线段A’B’的垂线，双击垂足，选中点P，“变换”—“缩放”—“缩放比1/2”，选中点P和新得到的点P’，“构造”—“轨迹”。
6.—“图象”—；7.，颜色为黄色。
8.隐藏直线，垂线，弧，点P，P’，A’，B’，线段CP’。
圆锥的侧面展开图圆锥的侧面展开图圆锥是一种立体图形，由一个圆形底面和一个顶点连接的直线组成。
在几何学中，我们经常使用侧面展开图来描述立体图形的形状和结构。
侧面展开图是将立体图形展开，使我们能够更好地理解其构造和组成。
首先，我们来看一下圆锥的基本特征。
圆锥的底面是一个圆形，用于提供稳定的支撑面。
圆锥的侧面是由从顶点连接到底面边缘的直线组成，这些直线被称为母线。
圆锥的顶点是连接底面和侧面的中心点。
为了绘制圆锥的侧面展开图，我们需要将圆锥展开成一个平面图形。
这可以通过将侧面按照一定顺序剪开，并展开到一个平面上来实现。
在展开的过程中，我们需要保持底面的圆形形状不变，并确保侧面的母线与底面保持相对位置不变。
展开后的侧面图是由一系列直线段构成的。
这些直线段代表了圆锥的侧面母线。
从顶点开始，我们可以看到侧面的直线段逐渐向底面延伸，并最终连接到底面边缘上。
展开后的侧面图呈现出一种锥形的形状，底面呈圆形，顶点在图形的中心位置。
圆锥的侧面展开图能够帮助我们更好地理解圆锥的结构和构造。
通过展开图，我们可以清晰地看到圆锥的母线如何连接到底面，并形成一个锥形的形状。
展开图还可以帮助我们计算圆锥的表面积和体积，以及分析其特性和功能。
在实际应用中，圆锥的侧面展开图被广泛应用于制作纸模、设计建筑物、制作工艺品等领域。
通过将圆锥展开成一个平面图形，我们可以更方便地制作和操作这些物品，并确保其形状和结构的准确性。
总结一下，圆锥的侧面展开图是将圆锥展开成一个平面图形以展示其构造和形状的方法。
通过展开图，我们可以更好地理解圆锥的特征和结构，并在应用中应用展开图进行设计和制作。
展开图提供了一种直观和清晰的方式来描述圆锥的形状和组成，对于学习和应用圆锥的几何学非常有帮助。
圆锥的侧面积和全面积教学设计与评析邓其有效的数学学习活动离不开学生主动参与，缺乏学生参与的教学，实际上是低效甚至无效的教学。
但是，教学活动一定要结合学生生活数学实际，只有具体、直观、生动、实践性的教学活动才能激发学生主动参与的兴趣，才能给学生直接的体验、直观的感受，留给学生“形象”的记忆，帮助学生跨过数学抽象、难以接受、难以理解、难以运用的门坎。
在此，我仅以“圆锥的侧面积和全面积”教学设计来呈现具体、直观、生动、实践性的教学活动。
教学目标：1、了解圆锥得结构，会计算圆锥的侧面积和全面积，并会解决实际问题。
2、增强学生用数学知识解决实际问题的能力，引导学生对圆锥展开图的认识，培养学生空间观念，激发学生的好奇心和求知欲，并在运用数学知识解答实际问题的活动中获取成功的体验，建立学习的自信心。
教学重点：圆锥的侧面积和全面积的计算。
教学难点1、明确扇形中各元素与圆锥各个元素之间的关系。
2、难点突破对策：自制教具，展开圆锥的侧面，呈现具体、直观、生动的生活数学。
教学过程：一、创设情景，引入课题引导学生复习弧长公式和扇形面积公式。
展现用纸片制作的圆锥，让学生观察，生活中见过圆锥吗？如何计算制作圆锥的这张纸的面积呢？【评析】复习已学知识点，为探究新知识做好准备，通过展现圆锥模型，获取生活数学，提出问题，引出课题，激发学生的好奇心和求知欲。
符合“数学来源于生活实际”的理念。
二、引导观察，探究新知1、认识圆锥引导学生观察圆锥，看到圆锥那些部分，再引导学生用尺规作图法做出立体图形（如图1）。
请观察图1，圆锥可以由什么图形旋转二而得？引导学生旋转手中的三角尺（以个边所在的直线为旋转轴）……【评析】提高学生观察能力、动手能力，培养学生空间观念。
将生活问题数学化，让学生从一些简单的实例中，不断体会从现实世界中寻找数学模型、建立数学关系的方法。
2、圆锥的三个元素及其关系圆锥的母线（l）:圆锥底面圆上任意一点与圆锥顶点的连线段。
