2017届苏教版 合情推理与演绎推理 课时跟踪检测

第1讲 合情推理与演绎推理 自主梳理1．归纳推理定义：根据一类事物中部分事物具有某种属性，推断该类事物中每一个事物都有这种属性，我们将这种推理方式称为归纳推理．2．归纳推理的思维过程大致是实验、观察→概括、推广→猜测一般性结论．3．归纳推理具有如下的特点：(1)归纳推理是由部分到整体，由个别到一般 的推理；(2)由归纳推理得到的结论不一定 正确；(3)归纳推理是一种具有创造性的推理．4．类比推理：由于两类不同对象具有某些类似的特征，在此基础上，根据一类对象的其他特征，推断另一类对象也具有类似的其他特征 ，我们把这种推理过程称为类比推理． 类比推理是两类事物特征之间的推理．5．合情推理：合情推理是根据实验 和实践的结果、个人的经验和直觉、已有的事实 和正确的结论(定义、公理、定理等)，推测出某些结果的推理方式．合情推理的结果不一定正确．6．在数学中，证明一个命题，就是根据命题的条件和已知的定义、公理、定理，利用演绎推理的法则将命题推导出来．7．演绎推理三段论：探究点一：归纳推理在数列中的应用例1 在数列{a n }中，a 1＝1，a n ＋1＝2a n 2＋a n ，n ∈N *，猜想这个数列的通项公式，这个猜想正确吗？请说明理由．解 在{a n }中，a 1＝1，a 2＝2a 12＋a 1＝23，a 3＝2a 22＋a 2＝12＝24，a 4＝2a 32＋a 3＝25，…，所以猜想{a n }的通项公式为a n ＝2n ＋1.这个猜想是正确的，证明如下：因为a 1＝1，a n ＋1＝2a n 2＋a n ，所以1a n ＋1＝2＋a n 2a n ＝1a n ＋12，即1a n ＋1－1a n ＝12，所以数列⎩⎨⎧⎭⎬⎫1a n 是以1a 1＝1为首项，12为公差的等差数列，所以1a n ＝1＋(n －1)×12＝12n ＋12，所以通项公式a n ＝2n ＋1变式迁移1 已知数列{a n }满足a 1＝1，a n ＋1＝2a n ＋1(n ＝1,2,3，…)(1)求a 2，a 3，a 4，a 5；(2)归纳猜想通项公式a n .解 (1)当n ＝1时，知a 1＝1，由a n ＋1＝2a n ＋1得a 2＝3，a 3＝7，a 4＝15，a 5＝31. (2)由a 1＝1＝21－1，a 2＝3＝22－1，a 3＝7＝23－1，a 4＝15＝24－1，a 5＝31＝25－1，可归纳猜想出a n ＝2n －1(n ∈N *)．探究点二：归纳推理在图形变化中的应用例2 在法国巴黎举行的第52届世乒赛期间，某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品，其中第1堆只有一层，就一个球；第2,3,4，…堆最底层(第一层)分别按图所示方式固定摆放，从第二层开始，每层的小球自然垒放在下一层之上，第n 堆第n 层就放一个乒乓球，以f (n )表示第n 堆的乒乓球总数，则f (3)＝10_；f (n )＝n n ＋1n ＋26(答案用含n 的代数式表示)．解析 观察图形可知：f (1)＝1，f (2)＝4，f (3)＝10，f (4)＝20，…，故下一堆的个数是上一堆个数加上下一堆第一层的个数，即f (2)＝f (1)＋3；f (3)＝f (2)＋6；f (4)＝f (3)＋10；…；f (n )＝f (n －1)＋n n ＋12.将以上(n －1)个式子相加可得 f (n )＝f (1)＋3＋6＋10＋…＋n n ＋12＝12[(12＋22＋…＋n 2)＋(1＋2＋3＋…＋n )] ＝12[16n (n ＋1)(2n ＋1)＋n n ＋12]＝n n ＋1n ＋26. 变式迁移2：在平面内观察：凸四边形有2条对角线，凸五边形有5条对角线，凸六边形有9条对角线，…由此猜想凸n (n ≥4且n ∈N *)边形有几条对角线？解 凸四边形有2条对角线，凸五边形有5条对角线，比凸四边形多3条，凸六边形有9条对角线，比凸五边形多4条，于是猜想凸n 边形比凸(n －1)边形多(n －2)条对角线．于是猜想凸n 边形比凸(n －1)边形多(n －2)条对角线．探究点三：归纳推理在算式问题中的应用例3 观察下列等式，并从中归纳出一般法则．(1)1＝12，1＋3＝22，1＋3＋5＝32，1＋3＋5＋7＝42，1＋3＋5＋7＋9＝52，……(2)1＝12，2＋3＋4＝32，3＋4＋5＋6＋7＝524＋5＋6＋7＋8＋9＋10＝72，5＋6＋7＋8＋9＋10＋11＋12＋13＝92，……解 (1)对于(1)，等号左端是整数，且是从1开始的n 项的和，等号的右端是项数的平方； 对于(2)，等号的左端是连续自然数的和，且项数为2n －1，等号的右端是项数的平方．∴(1)猜想结论：1＋3＋5＋…＋(2n －1)＝n 2(n ∈N *)．(2)猜想结论：n ＋(n ＋1)＋…＋[n ＋(3n －2)]＝(2n －1)2(n ∈N *)．变式迁移3：在△ABC 中，不等式1A ＋1B ＋1C ≥9π成立；在四边形ABCD 中，不等式1A ＋1B ＋1C ＋1D ≥162π成立；在五边形ABCDE 中，不等式1A ＋1B ＋1C ＋1D ＋1E ≥253π成立．猜想在n 边形A 1A 2…A n 中成立的不等式为1A 1＋1A 2＋…＋1A n ≥n 2n －2π(n ≥3且n ∈N *).． 探究点四：类比推理在几何中的应用例4：在平面内，可以用面积法证明下面的结论：从三角形内部任意一点，向各边引垂线，其长度分别为p a ，p b ，p c ，且相应各边上的高分别为h a ，h b ，h c ，则有p a h a ＋p b h b ＋p c h c＝1. 请你运用类比的方法将此结论推广到四面体中并证明你的结论．解 类比：从四面体内部任意一点向各面引垂线，其长度分别为p a ，p b ，p c ，p d ，且相应各面上的高分别为h a ，h b ，h c ，h d .则有p a h a ＋p b h b ＋p c h c ＋p d h d ＝1.证明如下： p a h a ＝13S △BCD ·p a 13S △BCD ·h a＝V P —BCD V A —BCD ，同理有p b h b ＝V P —CDA V B —CDA ，p c h c ＝V P —BDA V C —BDA ，p d h d ＝V P —ABC V D —ABC ，V P —BCD＋V P —CDA ＋V P —BDA ＋V P —ABC ＝V A —BCD ，∴p a h a ＋p b h b ＋p c h c ＋p d h d ＝V P —BCD ＋V P —CDA ＋V P —BDA ＋V P —ABC V A —BCD＝1. 变式迁移:4：在Rt △ABC 中，若∠C ＝90°，AC ＝b ，BC ＝a ，则△ABC 的外接圆半径r ＝a 2＋b 22，将此结论类比到空间有在三棱锥A —BCD 中，若AB 、AC 、AD 两两互相垂直，且AB ＝a ，AC ＝b ，AD ＝c ，则此三棱锥的外接球半径R ＝a 2＋b 2＋c 22探究点五：定义、定理或性质中的类比例2 在等差数列{a n }中，若a 10＝0，证明：等式a 1＋a 2＋…＋a n ＝a 1＋a 2＋…＋a 19－n (n <19，n ∈N *)成立，并类比上述性质相应的在等比数列{b n }中，若b 9＝1，则有等式______成立． 解析 在等差数列{a n }中，由a 10＝0，得a 1＋a 19＝a 2＋a 18＝…＝a n ＋a 20－n ＝a n ＋1＋a 19－n ＝2a 10＝0，∴a 1＋a 2＋…＋a n ＋…＋a 19＝0，即a 1＋a 2＋…＋a n ＝－a 19－a 18－…－a n ＋1，又∵a 1＝－a 19，a 2＝－a 18，…，a 19－n ＝－a n ＋1，∴a 1＋a 2＋…＋a n ＝－a 19－a 18－…－a n ＋1＝a 1＋a 2＋…＋a 19－n .相应地，类比此性质在等比数列{b n }中，可得b 1b 2…b n ＝b 1b 2…b 17－n ，(n <17，n ∈N *)．变式迁移5：设等差数列{a n }的前n 项和为S n ，则S 4，S 8－S 4，S 12－S 8，S 16－S 12成等差数列．类比以上结论有：设等比数列{b n }的前n 项积为T n ，则T 4，T 8T 4:，T 12T 8_，T 16T 12成等比数列． 探究点三 演绎推理例3 在锐角三角形ABC 中，AD ⊥BC ，BE ⊥AC ，D 、E 是垂足．求证：AB 的中点M 到D 、E 的距离相等．证明 (1)因为有一个内角是直角的三角形是直角三角形，——大前提在△ABD 中，AD ⊥BC ，即∠ADB ＝90°，——小前提所以△ADB 是直角三角形．——结论(2)因为直角三角形斜边上的中线等于斜边的一半，——大前提而M 是Rt △ADB 斜边AB 的中点，DM 是斜边上的中线，——小前提所以DM ＝12AB .——结论同理EM ＝12AB ，所以DM ＝EM . 变式迁移3 已知：在空间四边形ABCD 中，点E ，F 分别是AB ，AD 的中点，如图所示，求证：EF∥平面BCD.证明 三角形的中位线平行于底边， 大前提点E 、F 分别是AB 、AD 的中点， 小前提所以EF ∥BD . 结论若平面外一条直线平行于平面内一条直线则直线与此平面平行， 大前提EF ⊄平面BCD ，BD ⊂平面BCD ，EF ∥BD ， 小前提EF ∥平面BCD . 结论课后小试身手一、选择题1．数列5,9,17,33，x，…中的x等于(B) A．47 B．65 C．63 D．1282．观察(x2)′＝2x，(x4)′＝4x3，(cos x)′＝－sin x，由归纳推理可得：若定义在R上的函数f(x)满足f(－x)＝f(x)，记g(x)为f(x)的导函数，则g(－x)等于(D) A．f(x) B．－f(x) C．g(x) D．－g(x)3．下列推理正确的是(D) A．把a(b＋c)与log a(x＋y)类比，则有log a(x＋y)＝log a x＋log a yB．把a(b＋c)与sin (x＋y)类比，则有sin (x＋y)＝sin x＋sin yC．把a(b＋c)与a x＋y类比，则有a x＋y＝a x＋a yD．把a(b＋c)与a·(b＋c)类比，则有a·(b＋c)＝a·b＋a·c4．下面几种推理是合情推理的是(C)①由圆的性质类比出球的有关性质；②由直角三角形、等腰三角形、等边三角形的内角和是180°，归纳出所有三角形的内角和都是180°；③张军某次考试成绩是100分，由此推出全班同学的成绩都是100分；④三角形内角和是180°，四边形内角和是360°，五边形内角和是540°，由此得凸多边形内角和是(n－2)·180°.A．①②B．①③C．①②④D．②④5．①归纳推理是由部分到整体的推理；②归纳推理是由一般到一般的推理；③演绎推理是由一般到特殊的推理；④类比推理是由特殊到一般的推理；⑤类比推理是由特殊到特殊的推理．上表述正确的是(D)A．①②③ B．②③④C．②④⑤D．①③⑤6．下列说法不正确的是(D) A．演绎推理是由一般到特殊的推理B．赋值法是演绎推理C．三段论推理的一个前提是肯定判断，结论为否定判断，则另一前提是否定判断D．归纳推理的结论都不可靠7．正弦函数是奇函数，f(x)＝sin(x2＋1)是正弦函数，因此f(x)＝sin (x2＋1)是奇函数．以上推理(C)A．结论正确B．大前提不正确C．小前提不正确D．全不正确8．“∵四边形ABCD是矩形，∴四边形ABCD的对角线相等．”以上推理的大前提是(B) A．正方形都是对角线相等的四边形B．矩形都是对角线相等的四边形C．等腰梯形都是对角线相等的四边形D．矩形都是对边平行且相等的四边形9．下列几种推理过程是演绎推理的是(A) A．5和22可以比较大小B．由平面三角形的性质，推测空间四面体的性质C．东升高中高二年级有15个班，1班有51人，2班有53人，3班有52人，由此推测各班都超过50人 D ．预测股票走势图10． 把下面在平面内成立的结论类比地推广到空间，结论仍然正确的是(B)A ．如果一条直线与两条平行线中的一条相交，则也与另一条相交B ．如果一条直线与两条平行线中的一条垂直，则也与另一条垂直C ．如果两条直线同时与第三条直线相交，则这两条直线相交或平行D ．如果两条直线同时与第三条直线垂直，则这两条直线平行二、选择题11． f (n )＝1＋12＋13＋…＋1n (n ∈N *)，计算得f (2)＝32，f (4)>2，f (8)>52，f (16)>3，f (32)>72，推测当n ≥2时，有f (2n )>n ＋22解析[f (4)＝f (22)>2＋22，f (8)＝f (23)>3＋22，f (16)＝f (24)>4＋22，f (32)＝f (25)＝5＋22.] 12． 已知sin 230°＋sin 290°＋sin 2150°＝32，sin 25°＋sin 265°＋sin 2125°＝32. 通过观察上述两等式的规律，请你写出一个一般性的命题：sin 2(α－60°)＋sin 2α＋sin 2(α＋60°)＝3213． 如图，观察图形规律，在其右下的的空格处画上合适的图形，应为 ①．14． 在等差数列{a n }中，若a n >0，公差d >0，则有a 4·a 6>a 3·a 7，类比上述性质，在等比数列{b n }中，若b n >0，q >1，则下列有关b 4，b 5，b 7，b 8的不等关系正确的是 ①．①b 4＋b 8>b 5＋b 7；②b 5＋b 7>b 4＋b 8；③b 4＋b 7>b 5＋b 8；④b 4＋b 5>b 7＋b 8.15． 类比平面直角坐标系中△ABC 的重点G (x ，y )的坐标公式⎩⎨⎧x ＝x 1＋x 2＋x 33y ＝y 1＋y 2＋y 33(其中A (x 1，y 1)、B (x 2，y 2)、C (x 3，y 3)，猜想以A (x 1，y 1，z 1)、B (x 2，y 2，z 2)、C (x 3，y 3，z 3)、D (x 4，y 4，z 4)为顶点的四面体A —BCD 的重点G (x ，y ，z )的公式为⎩⎪⎨⎪⎧ x ＝x 1＋x 2＋x 3＋x 44y ＝y 1＋y 2＋y 3＋y 44z ＝z 1＋z 2＋z 3＋z 44．16．对于平面上的点集Ω，如果连接Ω中任意两点的线段必定包含于Ω，则称Ω为平面上的凸集，给出平面上4个点集的图形如上图(阴影区域及其边界)：其中为凸集的是②③(写出所有凸集相应图形的序号)．三，解答题17．已知数列{a n }的前n 项和为S n ，a 1＝1且S n －1＋1S n＋2＝0(n ≥2)，计算S 1，S 2，S 3，S 4，并猜想S n 的表达式．解 当n ＝1时，S 1＝a 1＝1；当n ＝2时，1S 2＝－2－S 1＝－3，∴S 2＝－13；当n ＝3时，1S 3＝－2－S 2＝－53，∴S 3＝－35；当n ＝4时，1S 4＝－2－S 3＝－75，∴S 4＝－57.猜想：S n ＝－2n －32n －1(n ∈N *)．18．一条直线将平面分成2个部分，两条直线最多将平面分成4个部分．(1)3条直线最多将平面分成多少部分？(2)设n 条直线最多将平面分成f (n )部分，归纳出f (n ＋1)与f (n )的关系；(3)求出f (n )．解 (1)3条直线最多将平面分成7个部分．(2)f (n ＋1)＝f (n )＋n ＋1.(3)f (n )＝[f (n )－f (n －1)]＋[f (n －1)－f (n －2)]＋…＋[f (2)－f (1)]＋f (1)＝n ＋(n －1)＋(n －2) ＋…＋2＋2＝n 2＋n ＋22.19．如图所示，在△ABC 中，射影定理可表示为a ＝b ·cos C ＋c ·cos B ，其中a ，b ，c 分别为角A ，B ，C 的对边，类比上述定理，写出对空间四面体性质的猜想．解 如图所示，在四面体P －ABC 中，设S 1，S 2，S 3，S 分别表示△P AB ，△PBC ，△PCA ，△ABC 的面积，α，β，γ依次表示面P AB ，面PBC ，面PCA 与底面ABC 所成二面角的大小．我们猜想射影定理类比推理到三维空间，其表现形式应为：S ＝S 1·cos α＋S 2·cos β＋S 3·cos γ20．设a >0，f (x )＝e x a ＋a e x 是R 上的偶函数，求a 的值． 解 ∵f (x )是R 上的偶函数，∴f (－x )＝f (x )，∴(a －1a )(e x －1e )＝0对于一切x ∈R 恒成立，由此得a －1a＝0，即a 2＝1.又a >0，∴a ＝1.。

合情推理教学目标结合已学过的数学实例和生活中的实例，了解合情推理的含义，能利用归纳和类比进行简单的推理，体会并认识合情推理在数学发现中的作用．教学重点，难点归纳推理和类比推理的特点及其创新性和不严谨性．教学过程我们生活中有很多谚语，特别是关于农耕的，例如“瑞雪兆丰年〞“邋遢冬至干净年〞，以及一些看云识天气的方法，这些都是我们的祖先根据多年的观察总结归纳出来的经验．这些经验就是人们根据长期的实践经验进行归纳的结果农民观察天气，生物学家会去观察鸟类，心理学家会去观察行为和表情，比方说你们也会观察，总结出我上课写在黑板右侧的总是错的，或者我微微一笑，说明接下来就是一个具有挑战性的问题．当然一个对数学感兴趣的数学家就会去观察一些数字．一．问题情境数学教育家G．波利亚在其名著?数学与猜测?中对哥德巴赫猜测的推理过程进行了模拟演示：首先，波利亚说明：归纳法常常从观察开始．一个生物学家会观察鸟类的生活，一个晶体学家会观察晶体的形状，一个对数论有兴趣的数学家会观察整数1,2,3,4,5,…的性质．这一段表达说明：归纳从观察开始，而观察要有归纳的动因，即要有感兴趣、需研究的问题，归纳推理研究问题、发现规律的手段．接着，波利亚说：假设你想要观察鸟的生活并有可能获得有益的结论的话，那么你就应当对鸟稍有熟悉，对鸟感兴趣，甚至你应当喜欢鸟．同样，假设你要考察数，你就应当对它们感兴趣，并且对它们颇为熟悉，你应当会区别偶数和奇数，你应当知道平方数1,4,9,14,25,…以及素数2,3,5,7,11,13,17,19,23,29,…．这里，波利亚想要传达的意思是：对你感兴趣的问题你还需要对相关的知识有一定的了解，也即应该从你对这一课题中已经熟悉的、掌握的内容开始你的探究．波利亚又说：即使只有这一点朴素的知识，你也可能观察到一些东西．比方说你可能会碰到这样几个关系：3＋7＝103＋17＝20213＋17＝30并注意到它们之间的类似之处．它会使你想到：3,7,13,和17都是奇素数，10,20210都是偶数…．这三个偶数都能够表示为两个奇素数之和，那么其他偶数又怎么样呢？上述过程说明了归纳推理的非常重要的特征：从特殊情形开始，并且所有的特殊情形都要具有类似之处，这个类似之处正是归纳发现的根底．波利亚接着说：那么其他偶数又怎么样呢？它们也有类似的性质吗？当然头一个等于两个奇素数之和偶数是6＝3＋3．看看超过6的数，我们发现8＝3＋510＝3＋7＝5＋512＝5＋714＝3＋11＝7＋716＝3＋13＝5＋11．这样下去总是对的吗？波利亚想告诉我们的是，对从几个特殊情形经过归纳推理得到的结果不能轻信，需要进一步验证．只有在较多的归纳检验证实的根底上得到的结论才能使我们更有信心．最后，波利亚说：无论如何，所看到的这些个别情况，至少可以启发我们提出一个一般性的命题：任何一个大于4的偶数都是两个奇素数的和．至此，实现了归纳推理的目标：一个一般性的结论〔猜测〕．当然，波利亚还进一步说明了证明的必要性．从波利亚的这个案例我们可以发现，对归纳推理的教学应该突出说明以下几点：1、要使学生认识到归纳推理不是盲目的、毫无目的的尝试，科学发现更不是纯属偶然的巧合，必须有一定的内因的驱动和信念的支撑．2、归纳推理的三个特点：从特殊开始的推理；由归纳推理得到的结论仅仅“似真〞；归纳推理是一种创造性的推理．3、归纳推理的思维规程大致为：【活动一】1．观察以下等式，从中可以得出怎样的一般规律？猜测：任何一个正整数都能表示为四个数的平方和．2．在数列中，，通过计算，试猜测这个数列的通项公式．猜测3．前个正整数的和为，前个正整数的平方和从表中发现，于是猜测．归纳推理要具备下述几个要素：1．多个特例综合分析；特例共性的发现：要存在某种相似性；共性的概括：猜测．归纳推理需要大量的原始数据，这是一个漫长的过程，在大数据时代，电脑已局部取代了这个过程，例如分析你的上网数据，分析你的喜好进行广告推送．但我们还有另外一种常用的推理方法．在高中数学学习中，指数函数与对数函数的类比，等差数列和等比数列的类比，平面几何和立体几何的类比，圆和椭圆和双曲线抛物线的类比，实数与虚数的类比等．〔G波利亚的类比〕类比实数的加法与乘法，并列出它们类似的性质．在实数的加法与乘法之间，可以建立如下的对应关系：加〔＋〕乘〔×〕加数、被加数乘数、被乘数和积等等，它们具有以下类似的性质：试将平面上的圆与空间的球进行类比．圆的定义：平面内到一个定点的距离等于定长的点的集合． 球的定义：到一个定点的距离等于定长的点的集合． 圆 球 弦截面圆 直径 大圆 周长 外表积 圆面积球体积例如三角形的性质可以往几个方向类比：一般化为四边形，特殊化为正三角形，升维度为三棱锥，改平面为曲面等【活动二】1．选两个相关知识进行类比2．圆的方程是，那么过圆上一点的切线方程为．猜测新命题：1．类比推理是从特殊到特殊的推理，是寻找事物之间的共同或相似性质．类比的性质相似性越多，相似的性质与推测的性质之间的关系就越相关，从而类比得出的结论就越可靠．2．类比推理的一般步骤：〔1〕找出两类事物之间的相似性或者一致性．〔2〕用一类事物的性质去推测另一类事物的性质，得出一个明确的命题〔猜测〕．【活动三】1．设,为实数，满足，，求的最大值．解：设，那么，即，，将，两式相加得．根据以上解答过程进行类比，尝试解决下题：设,为实数，满足，，求的最大值．〔2021年江苏高考第13题〕设，由此可以求出，，而2021江苏高考数学卷中的题目就表达出多种形式的类比思想。

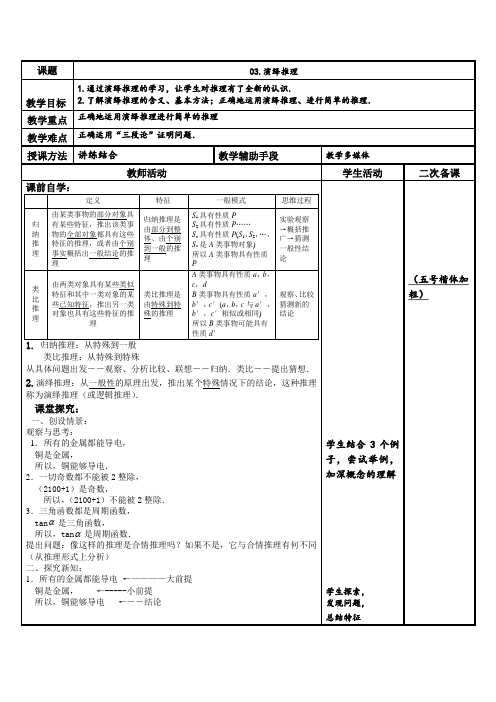
课题03.演绎推理教学目标1.通过演绎推理的学习，让学生对推理有了全新的认识.2.了解演绎推理的含义、基本方法；正确地运用演绎推理、进行简单的推理．教学重点正确地运用演绎推理进行简单的推理教学难点正确运用“三段论”证明问题．授课方法讲练结合教学辅助手段教学多媒体教师活动学生活动二次备课课前自学：定义特征一般模式思维过程归纳推理由某类事物的部分对象具有某些特征，推出该类事物的全部对象都具有这些特征的推理，或者由个别事实概括出一般结论的推理归纳推理是由部分到整体、由个别到一般的推理S1具有性质PS2具有性质P……S n具有性质P(S1，S2，…，S n是A类事物对象)所以A类事物具有性质P实验观察→概括推广→猜测一般性结论类比推理由两类对象具有某些类似特征和其中一类对象的某些已知特征，推出另一类对象也具有这些特征的推理类比推理是由特殊到特殊的推理A类事物具有性质a，b，c，dB类事物具有性质a′，b′，c′(a，b，c与a′，b′，c′相似或相同)所以B类事物可能具有性质d′观察、比较猜测新的结论1.归纳推理：从特殊到一般类比推理：从特殊到特殊从具体问题出发――观察、分析比较、联想――归纳．类比――提出猜想．2.演绎推理：从一般性的原理出发，推出某个特殊情况下的结论，这种推理称为演绎推理（或逻辑推理）．课堂探究：一、创设情景：观察与思考：1．所有的金属都能导电，铜是金属，所以，铜能够导电．2．一切奇数都不能被2整除，（2100+1）是奇数，所以，（2100+1）不能被2整除．3．三角函数都是周期函数，tanα是三角函数，所以，tanα是周期函数．提出问题：像这样的推理是合情推理吗？如果不是，它与合情推理有何不同（从推理形式上分析）二、探究新知：1．所有的金属都能导电←————大前提铜是金属，←-----小前提所以，铜能够导电←――结论学生结合3个例子，尝试举例，加深概念的理解学生探索，发现问题，总结特征（五号楷体加粗）。

教材分析：本课时所要探究的三角形中位线定理是学生以前从未接触过的内容。

因此，在教学中通过创设有趣的情境问题，激发学生的学习兴趣，注重新旧知识的联系，强调直观与抽象的结合，鼓励学生大胆猜想，大胆探索新颖独特的证明方法和思路，让学生充分经历“探索—发现—猜想—证明”这一过程，体会合情推理与演绎推理在获得结论的过程中发挥的作用，同时渗透归纳、类比、转化等数学思想方法。

通过本节课的学习，应使学生理解三角形中位线定理不仅指出了三角形的中位线与第三边的位置关系和数量关系，而且为证明线段之间的位置关系和数量关系（倍分关系）提供了新的思路，从而提高学生分析问题、解决问题的能力。

教学目标：1.知识目标（1）了解三角形中位线的概念。

（2）掌握三角形中位线定理的证明和有关应用。

2.能力目标（1）经历“探索—发现—猜想—证明”的过程，进一步发展推理论证能力。

（2）能够用多种方法证明三角形的中位线定理，体会在证明过程中所运用的归纳、类比、转化等数学思想方法。

（3）能够应用三角形的中位线定理进行有关的论证和计算，逐步提高学生分析问题和解决问题的能力。

3.情感目标通过学生动手操作、观察、实验、推理、猜想、论证等自主探索与合作交流的过程，激发学生的学习兴趣，让学生真正体验知识的发生和发展过程，培养学生的创新意识。

教学重点与难点：教学重点：三角形中位线的概念与三角形中位线定理的证明.教学难点：三角形中位线定理的多种证明。

教学过程：一、复习旧知，导入新课：什么是三角形的中线？请你能画出一个三角形的所有中线。

如图，已知△AEC中，AB=BC。

AD=DE，那么BD就叫三角形的中位线。

今天我们就来研究三角形中位线的有关知识。

二、自主学习：一个三角形中有几条中位线？1、一个三角形中有几条中位线？请你全部画出。

你能仿照三角形中线的定义给它下个定义吗？（通过与中线区别，抓住中位线的特征，把下定义的任务给了学生，培养了学生的概括能力）。

2、大家随便画一个三角形，并画出它的中位线，看看它的中位线与三角形的第三边之间存在什么关系？可以从两个方面去看：数量关系和位置关系。

课题01.合情推理（1）教学目标1.结合数学实例，了解归纳推理的含义；2.能利用归纳方法进行简单的推理.3.认识归纳推理在数学发现中的作用。

教学重点归纳推理的含义及应用教学难点引导和训练学生从已知的线索中归纳出正确的结论授课方法讲练结合教学辅助手段教学多媒体教师活动学生活动二次备课课前自学：1.归纳推理：把从个别事实中推演出一般性的结论的推理方法称为归纳推理．2.归纳推理的思维过程：3.归纳是从特殊到一般的过程。

4.由两类对象具有某些类似特征和其中一类对象的某些已知特征，推出另一类对象也具有这些特征的推理. 简言之，类比推理是由特殊到特殊的推理.课堂探究：一、创设情景：1、哥德巴赫猜想：观察4=2+2, 6=3+3, 8=5+3, 10=5+5, 12=5+7, 12=7+7, 16=13+3, 18=11+7, 20=13+7, ……, 50=13+37, ……, 100=3+97，猜测：任一偶数（除去2，它本身是一素数）可以表示成两个素数之和. 1742年写信提出，欧拉及以后的数学家无人能解，成为数学史上举世闻名的猜想. 1973年，我国数学家陈景润，证明了充分大的偶数可表示为一个素数与至多两个素数乘积之和，数学上把它称为“1+2”2.四色猜想：1852年，毕业于英国伦敦大学的弗南西斯.格思里来到一家科研单位搞地图着色工作时，发现了一种有趣的现象：“每幅地图都可以用四种颜色着色，使得有共同边界的国家着上不同的颜色.”，四色猜想成了世界数学界关注的问题.1976年，美国数学家阿佩尔与哈肯在美国伊利诺斯大学的两台不同的电子计算机上，用1200个小时，作了100亿逻辑判断，完成证明.二、探究新知：①概念：由某类事物的部分对象具有某些特征，推出该类事物的全部对象都具有这些特征的推理，或者由个别事实概括出一般结论的推理，称为归纳推理. 简言之，归纳推理是由部分到整体、由个别到一般的推理.②归纳练习：(i)由铜、铁、铝、金、银能导电，能归纳出什么结论？(ii)由直角三角形、等腰三角形、等边三角形内角和180度，能归纳出什么结论？(iii)观察等式：2221342,13593,13579164+==++==++++==，能得出怎样的结论？③讨论：(i)统计学中，从总体中抽取样本，然后用样本估计总体，是否属归纳推理？学生课前自学并完成填空通过阅读教材感受归纳推理的魅力从哥德巴赫猜想引出归纳推理概念实验、观察猜测一般性结论概括、推广。

第二章 合情推理与演绎推理§2.1.1.1合情推理(第一课时)一、教学目标：1、知识与技能：掌握归纳推理的技巧，并能运用解决实际问题。

2、过程与方法：通过“自主、合作与探究”实现“一切以学生为中心”的理念。

3、情感、态度与价值观：感受数学的人文价值，提高学生的学习兴趣，使其体会到数学学习的美感。

二、教学重点：归纳推理及方法的总结。

三、教学难点：归纳推理的含义及其具体应用。

四、教学过程：（一）探入与展示：1、推理 根据一个或几个已知的判断来确定一个新的判断的思维过程就叫推理. 推理一般由两部分组成：前提和结论2、（二）探读与思考引入1. 哥德巴赫猜想：观察4=2+2, 6=3+3, 8=5+3, 10=5+5, 12=5+7, 12=7+7, 16=13+3, 18=11+7, 20=13+7, ……, 50=13+37, ……, 100=3+97，猜测：任一偶数（除去2，它本身是一素数）可以表示成两个素数之和. 1742年写信提出，欧拉及以后的数学家无人能解，成为数学史上举世闻名的猜想. 1973年，我国数学家陈景润，证明了充分大的偶数可表示为一个素数与至多两个素数乘积之和，数学上把它称为“1+2”.引入 2. 费马猜想：法国业余数学家之王—费马（1601-1665）在1640年通过对020213F =+=，121215F =+=，2222117F =+=，32321257F =+=，4242165537F =+=的观察，发现其结果都是素数，于是提出猜想：对所有的自然数n ，任何形如221nn F =+的数都是素数. 后来瑞士数学家欧拉，发现5252142949672976416700417F =+==⨯不是素数，推翻费马猜想.引入3：1．由铜、铁、铝、金、银等金属都能导电，猜想：一切金属都能导电．2．由三角形内角和为180°，凸四边形内角和为360°，凸五边形内角和为540°，猜想：凸n 边形内角和为(n －2)·180°.1、归纳推理的定义：由某类事物的部分对象具有某些特征，推出该类事物的全部对象都具有这些特征的推理，或者有个别事实概括出一般结论的推理，称为归纳推理(简称归纳)。