- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
������������
递推式两边取倒数,便可构造等差数列 ������ ,即可求解. ������
1
3 ������������ 【例题 6】 已知数列{an}中,a1= ,an+1= ,求{an}的通项公式. 5 2������������ +1 1 2������������ +1 1 解:由已知得������ = ������ = ������ +2, ������ ������ ������+1 1 1 即 − =2. ������������+1 ������������ 1 1 5 所以 ������ 是等差数列,公差为 2,其首项为������ = 3, ������ 1 1 5 6������-1 3 故 = +2(n-1)= ,故 an= . ������������ 3 3 6������-1
-10-
本章整合
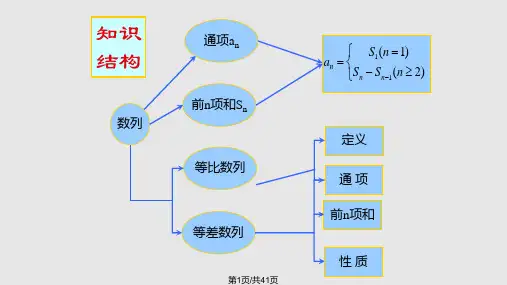
知识网络
专题探究
专题一
专题二
专题二 数列求和的常用方法
数列求和是数列部分的重要内容,也是高考的重要考点之一.对于数列求和问题, 一般是先观察数列的特点和规律,如果通项公式能够求出,可先求出通项公式再决 定使用哪种求和方法.下面介绍几种常用的求和方法. 1.公式法 公式法是数列求和的最常用方法之一,可直接利用等差数列、等比数列的求和
解:∵数列{an}的前n项和为Sn=2n-1,
∴{an}为等比数列. ∵a1=S1=21-1=1,a2=S2-S1=3-1=2,
∴数列{an}的公比q=2.
2 2} ∴数列 {������������ 是首项为 ������1=1,公比为q2=4的等比数列.
2 ∴������1 2 2 + ������2 +…+������������
∴an=f(n-1)+f(n-2)+…+f(2)+f(1)+a1.
-5-
本章整合
知识网络
专题探究
专题一
专题二
为了书写方便,也可以用横式来写:
∵当n≥2时,an-an-1=f(n-1), ∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=f(n-1)+f(n-2)+…+f(2)+f(1)+a1.
本章整合
知识网络
专题探究
专题一
专题二
专题一 数列通项公式的求法
数列的通项公式是给出数列的主要方式,其本质就是函数的解析式.围绕数列的 通项公式,不仅可以判断数列的类型,研究数列的项的变化趋势与规律,而且有利于 求数列的前n项和.求数列的通项公式是数列的核心问题之一.下面介绍几种常用
的求法.
-1-
本章整合
������������ =f(n-1), ������������-1
-8-
本章整合
知识网络
专题探究
专题一
专题二
【例题 5】 已知数列{an}中,a1= ,an+1= 解:因为 an+1=3������+2an,
������ 所以������ ������ ������-1 1 3������-1
3 6 1 1 1
故 an=3+2(n-1)=2n+1,bn=8n-1.
-15-
本章整合
知识网络
专题探究
专题一
专题二
(2)∵Sn=3+5+…+(2n+1)=n(n+2),
2 ������ -1 . 3 ������ 2 2
-4-
本章整合
知识网络
专题探究
专题一
专题二
3.累加法 对于形如an+1-an=f(n)型的递推公式求通项公式.
(1)当f(n)=d为常数时,{an}为等差数列,则an=a1+(n-1)d;
(2)当f(n)为关于n的函数时,用叠加法. 方法如下:由an+1-an=f(n),得 当n≥2时,an-an-1=f(n-1), an-1-an-2=f(n-2), …… a3-a2=f(2), a2-a1=f(1). 以上n-1个等式叠加,得 an-a1=f(n-1)+f(n-2)+…+f(2)+f(1),
2������
������ ������+1
(2 -1)(2
-1)
,求其
=
所以 Tn=a1+a2+…+an =
21 -1
−
1
+
1 22 -1
−
1
23 -1
+…+
=1-
2������+1 -1
.
-14-
本章整合
知识网络
专题探究
专题一
专题二
【例题 13】 等差数列{an}的各项均为正数,a1=3,前 n 项和为 Sn,{bn}为等比数列,b1=1,且 b2S2=64,b3S3=960. (1)求 an 与 bn; (2)求������ + ������ +…+������ . ������ 1 2 解:(1)设{an}的公差为 d,{bn}的公比为 q, 则 d 为正数,an=3+(n-1)d,bn=qn-1. ������2 ������2 = (6 + ������)������ = 64, 依题意,得 ������3 ������3 = (9 + 3������)������2 = 960. ������ = - 5 , ������ = 2, 解得 或 (舍去). 40 ������ = 8 ������ =
1 ������(������+1) 6 2 ������(������+1)(2������+1+3) 1 = = n(n+1)(n+2). 6 3
= n(n+1)(2n+1)+
-12-
本章整合
知识网络
专题探究
专题一
专题二
2 2 2 + ������2 +…+������������ . 【例题11】 已知数列{an}的前n项和为Sn=2n-1,求 ������1
=
= 5,
2
3������-4 3������-7 5 2 1 · · …· · · 8 5 2 3������-1 3������-4
=
1 . 3������-1
-9-
本章整合
知识网络
专题探究
专题一
专题二
5.构造辅助数列法 (1)取倒数构造法
������ 对于满足 an+1=������������ + (其中 p,q 为常数且 p,q≠0)形式的数列,可将 ������ ������
【例题 12】 已知数列{an}的通项公式为 an= 前 n 项和 Tn. 解:由于 an=
1 1 22 -1 2������ (2������ -1)(2������+1 -1) 1 1 − , 2������ -1 2������+1 -1 1 1 − 2������ -1 2������+1 -1
4.累乘法
为等比数列,an=a1qn-1. (2)当 f(n)为关于 n 的函数时,用累乘法. 由
������������+1 =f(n),得 ������������
n≥2 时,
������������ ������������-1 ������2 ∴an=������ ·������ · …· · a1=f(n-1)· …· f(1)· a1. ������ 1 ������-1 ������-2
1 2
3������-1 an(n≥1),求 an. 3������+2
=
3������-4 ������������-1 , ������ 3������-1 ������-2
又 a1=2,所以 =
3������-7 ������ 5 ������ ,…,������3 = 8 , ������2 3������-4 2 1 ������������ ������������-1 ������3 ������2 an=������ ·������ · …· ·������ · a1 ������ 2 1 ������-1 ������-2
������ 2 2������ ������2 ������2 1 n 1 [1-(������ ) ] 1 (1-������ ) 1× (1-4 ) = = = = (4 -1). 3 1-������2 1-������2 1-4 ������
-13-
本章整合
知识网络
专题探究
专题一
专题二
2.裂项相消法 对于裂项后明显有能够相消的项的一类数列,在求和时常用“裂项法”,对于分式 的求和多利用此法.解题时可用待定系数法对通项公式进行拆项,相消时应注意消 去的项的规律,即消去哪些项,保留哪些项.
∴数列{an}的通项公式为 an=2×3n-
1
������(������-1) 1 − 2. 2
-7-
本章整合
知识网络
专题探究
专题一
专题二
������������+1 对于形如 ������ =f(n)型的递推公式求通项公式. ������ ������������+1 (1)当 f(n)为常数时,即 ������ =q(其中 q 是不为 0 的常数),此时数列 ������
知识网络
专题探究
专题一
专题二
1.观察法 已知数列前若干项,求该数列的通项公式时,一般对所给的项观察分析,寻找规 律,从而根据规律写出此数列的一个通项公式. 【例题1】 写出下列两个数列的一个通项公式: