下载文档原格式
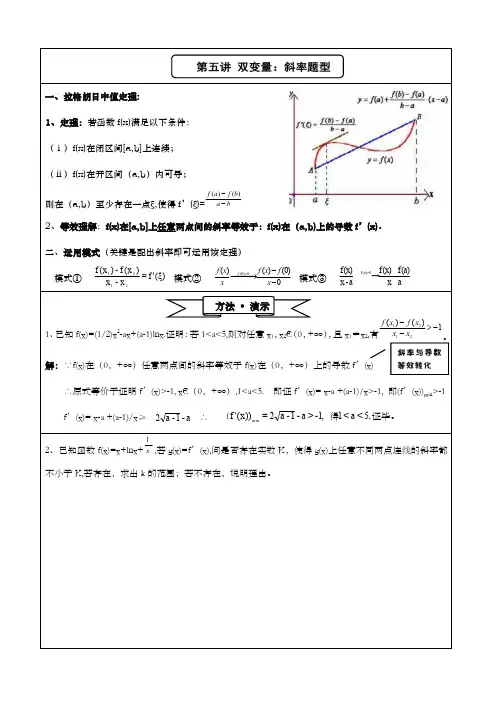
拉格朗日中值定理拉格朗日中值定理：若)(x f 满足在[]b a ,上连续，在()b a ,内可导，则在()b a ,内至少存在一点ξ使得()()()'f b f a f b a-=-ξ 几何意义：割线斜率必等于中间某点的切线斜率推论1： 若在区间()b a ,内导函数0)('≡x f ，则在区间()b a ,内)(x f 为一常数推论2： 若在区间()b a ,内函数)(x f ，)(x g 满足)()(''x g x f =，则在区间()b a ,内有c x g x f +=)()(，c 为常数典例剖析例题1证明：y x y x -≤-sin sin例题2 试证明：当[)+∞∈,1x 时，2ln 11ln ≥⎪⎭⎫ ⎝⎛+x x例题3 已知)0(,21ln )(2>+=a x x a x f ，对于任意两个不等的正数21,x x 都有 2)()(1212>--x x x f x f 恒成立，求a 的取值范围例题4 已知二次函数)(x f 满足：①在1=x 时有极值，②图像过点（0，-3）且在该点处的切线与直线02=+y x 平行（1）求)(x f 的解析式（2）若)(x e f y =上任意两点的连线斜率恒大于a a 1+，求a 的取值范围。
例题5 已知x a xx x f ln 2)(2++=，0>x ，)(x f 的导函数为)('x f ，对于任意两个不等 正数21,x x ，当4≤a 时，证明：212'1')()(x x x f x f ->-例题6 设)(x f 在[]1,0可导，且1)(0<<x f ，又对于()1,0内所有的点x 满足1)('-≠x f ，证明：方程01)(=-+x x f 在()1,0内有唯一实数根。
强化训练1.已知)1(,21)(,ln )(2>-==b bx x x g x x f ，对于区间()2,1内任意两个不等正数21,x x 都有)()()()(2121x g x g x f x f ->-恒成立，求b 的取值范围2.已知1ln )1()(2+++=ax x a x f（1）讨论)(x f 的单调性（2）设1-<a ，如果对于任意()∞+∈，0,21x x ，都有21214)()(x x x f x f -≥-，求a 的取值范围。
一拉格朗日中值定理拉格朗日中值定理，又被称为有限增量定理，是微积分中的一个基本定理。
拉格朗日中值公式的形式其实就是泰勒公式的一阶展开式的形式。
在现实应用当中，拉格朗日中值定有着很重要的作用。
拉格朗日中值定理是所有的微分中值定理当中使用最为普遍的定理。
拉格朗日中值定理的形成和发展过程都显示出了数学当中的一个定理的发展是一个推翻陈旧，出现创新的一个进程。
发现一些新的简单的定理去替代旧的复杂的定理，就是由初级走向高级。
用现代的语言来描述，在一个自变量x从x变为x+1的过程中，如果函数f(x)本身就是一个极限值，那么函数f(x+1)的值也应该是一个极限值，其值就应该和f(x)的值近似相等，即这就是非常著名的费马定律，当一个函数在x=a处可以取得极值，并且函数是可导函数，则′。
著名学者费马再给出上述定理时，此时的微积分研究理论正处于初始阶段，并没有很成熟的概念，没有对函数是否连续或者可导作出限制，因此在现代微积分理论成熟阶段这种说法就显得有些漏洞。
在所有的微分中值定理中，最重要的定理就是拉格朗日中值定理。
最初的拉格朗日中值定理和现在成熟的拉格朗日中值定理是不一样的，最初的定理是函数f(x)在闭区间[a,b]内任取两点和，并且函数在此闭区间内是连续的，′的最大值为A，′最小值为B，则的值必须是A和B之间的一个值。
这是拉格朗日定理最初的证明。
下述就是拉格朗日中值定理所要求满足的条件。
如果存在一个函数满足下面两个条件，（1）函数f 在闭区间[a，b]上连续；（2）函数f 在开区间（a，b）内可导；那么这个函数在此开区间内至少存在着一点，使得′ξ.拉格朗日中值定理是导数的一个延伸概念，在导数运算中是的很基本概念。
例1：函数，即′。
当在开区间∞时，有′，在开区间∞单调递增；当在开区间∞时，有′，f(x)在开区间∞单调递减。
在，有′，。
由上述例子说明，想要确定一个函数的单调性可以通过求得这个函数的一阶导数来求得判断单调区间。
x ‒ x 一 拉格朗日中值定理拉格朗日中值定理，又被称为有限增量定理，是微积分中的一个基本定理。
拉格朗日中值公式的形式其实就是泰勒公式的一阶展开式的形式。
在现实应用当中，拉格朗日中值定有着很重要的作用。
拉格朗日中值定理是所有的微分中值定理当中使用最为普遍的定理。
拉格朗日中值定理的形成和发展过程都显示出了数学当中的一个定理的发展是一个推翻陈旧，出现创新的一个进程。
发现一些新的简单的定理去替代旧的复杂的定理，就是由初级走向高级。
用现代的语言来描述，在一个自变量x 从x 变为x+1 的过程中，如果函数f(x) 本身就是一个极限值，那么函数 f(x+1)的值也应该是一个极限值，其值就应该和 f(x)的值近似相等，即f(x + 1) ‒ f(x)1≈ 0这就是非常著名的费马定律，当一个函数f(x)在 x=a 处可以取得极值，并且函数是可导函数，则f '(x) = 0。
著名学者费马再给出上述定理时，此时的微积分研究理论正处于初始阶段，并没有很成熟的概念，没有对函数是否连续或者可导作出限制，因此在现代微积分理论成熟阶段这种说法就显得有些漏洞。
在所有的微分中值定理中，最重要的定理就是拉格朗日中值定理。
最初的拉格朗日中值定理和现在成熟的拉格朗日中值定理是不一样的，最初的定理是函数 f(x)在闭区间[a,b]内任取两点x 0和x 1，并且函数f(x)在此闭区间内是连续的，f ' (x)的最大值为 A ，f '(x)最小值为 B ，则f(x 1) ‒ f(x 0)的值必须是 A 和 B 之间的一个值。
1 0这是拉格朗日定理最初的证明。
下述就是拉格朗日中值定理所要求满足的条件。
如果存在一个函数满足下面两个条件，（1）函数 f 在闭区间[a ，b]上连续； （2）函数 f 在开区间（a ，b ）内可导；那么这个函数在此开区间内至少存在着f(b) ‒ f(a)一点尉，使得f'(ξ) =b ‒ a.拉格朗日中值定理是导数的一个延伸概念，在导数运算中是的很基本概念。
拉格朗⽇中值定理⼀拉格朗⽇中值定理拉格朗⽇中值定理，⼜被称为有限增量定理，是微积分中的⼀个基本定理。
拉格朗⽇中值公式的形式其实就是泰勒公式的⼀阶展开式的形式。
在现实应⽤当中，拉格朗⽇中值定有着很重要的作⽤。
拉格朗⽇中值定理是所有的微分中值定理当中使⽤最为普遍的定理。
拉格朗⽇中值定理的形成和发展过程都显⽰出了数学当中的⼀个定理的发展是⼀个推翻陈旧，出现创新的⼀个进程。
发现⼀些新的简单的定理去替代旧的复杂的定理，就是由初级⾛向⾼级。
⽤现代的语⾔来描述，在⼀个⾃变量x从x变为x+1的过程中，如果函数f(x)本⾝就是⼀个极限值，那么函数f(x+1)的值也应该是⼀个极限值，其值就应该和f(x)的值近似相等，即这就是⾮常著名的费马定律，当⼀个函数在x=a处可以取得极值，并且函数是可导函数，则。
著名学者费马再给出上述定理时，此时的微积分研究理论正处于初始阶段，并没有很成熟的概念，没有对函数是否连续或者可导作出限制，因此在现代微积分理论成熟阶段这种说法就显得有些漏洞。
在所有的微分中值定理中，最重要的定理就是拉格朗⽇中值定理。
最初的拉格朗⽇中值定理和现在成熟的拉格朗⽇中值定理是不⼀样的，最初的定理是函数f(x)在闭区间[a,b]内任取两点，并且函数在此闭区间内是连续的，的最⼤值为A，最⼩值为B，则的值必须是A和B之间的⼀个值。
这是拉格朗⽇定理最初的证明。
下述就是拉格朗⽇中值定理所要求满⾜的条件。
如果存在⼀个函数满⾜下⾯两个条件，（1）函数f 在闭区间[a，b]上连续；（2）函数f 在开区间（a，b）内可导；那么这个函数在此开区间内⾄少存在着⼀点，使得.拉格朗⽇中值定理是导数的⼀个延伸概念，在导数运算中是的很基本概念。
例1：函数f(x)在开区间在由上述例⼦说明，想要确定⼀个函数的单调性可以通过求得这个函数的⼀阶导数来求得判断单调区间。
当⼀个函数在某个确定的区间内，存在着；内时，那么这⼀点就是这个函数的极值点。
在例1中，当1在拉格朗⽇中值定理中，有两个要求条件，⼀个是在⼀个闭区间内连续，⼀个是在相同期间开区间可导，不满⾜这两个条件，拉格朗⽇中值定理在此种情况下是没有意义的。
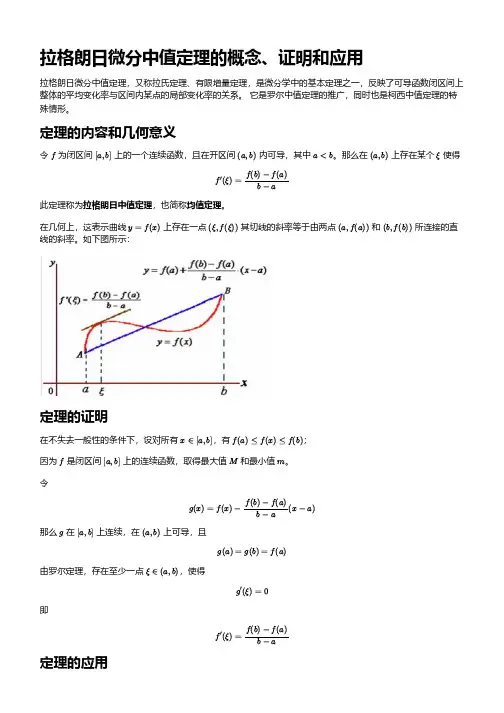
拉格朗日微分中值定理的概念、证明和应用拉格朗日微分中值定理，又称拉氏定理、有限增量定理，是微分学中的基本定理之一，反映了可导函数闭区间上整体的平均变化率与区间内某点的局部变化率的关系。
它是罗尔中值定理的推广，同时也是柯西中值定理的特殊情形。
定理的内容和几何意义令f为闭区间[a,b]上的一个连续函数，且在开区间(a,b)内可导，其中a<b。
那么在(a,b)上存在某个ξ使得f′(ξ)=f(b)−f(a)b−a此定理称为拉格朗日中值定理，也简称均值定理。
在几何上，这表示曲线y=f(x)上存在一点(ξ,f(ξ))其切线的斜率等于由两点(a,f(a))和(b,f(b))所连接的直线的斜率。
如下图所示：定理的证明在不失去一般性的条件下，设对所有x∈[a,b]，有f(a)≤f(x)≤f(b)；因为f是闭区间[a,b]上的连续函数，取得最大值M和最小值m。
令g(x)=f(x)−f(b)−f(a)b−a(x−a)那么g在[a,b]上连续，在(a,b)上可导，且g(a)=g(b)=f(a)由罗尔定理，存在至少一点ξ∈(a,b)，使得g′(ξ)=0即f′(ξ)=f(b)−f(a)b−a定理的应用拉格朗日中值定理在微分学中有着广泛的应用，例如：证明函数单调性、极值、凹凸性等性质；估计函数误差、求函数极限、判断函数收敛性等问题；推导洛必达法则、泰勒公式、积分第一中值定理等重要结论。
下面举几个例子说明。
例1：证明函数单调性设f(x)在[a,b]上连续，在(a,b)内可导，且对任意x∈(a,b)有f′(x)>0，则f(x)在[a,b]上单调递增。
证明：任取x1,x2∈[a,b]且x1<x2，由拉格朗日中值定理，存在ξ∈(x1,x2)使得f′(ξ)=f(x2)−f(x1) x2−x1由于f′(ξ)>0且x2−x1>0，所以有f(x2)−f(x1)>0即f(x2)>f(x1)这说明f(x)在[a,b]上单调递增。
高等数学拉格朗日中值定理高等数学拉格朗日中值定理是微积分中的一项重要定理，它被广泛应用于求解函数的极值、证明函数的性质以及推导其他数学定理等方面。
拉格朗日中值定理是法国数学家约瑟夫·路易斯·拉格朗日于18世纪提出的，它建立在导数的基础上，描述了函数在某个区间内的平均变化率与其导数在该区间内某点的值之间的关系。
拉格朗日中值定理的表述如下：若函数f(x)在闭区间[a, b]上连续，在开区间(a, b)内可导，那么在(a, b)内至少存在一个点c，使得f(b) - f(a) = f'(c)(b - a)。
简单来说，拉格朗日中值定理告诉我们，对于任意一段曲线，至少存在一个点，该点的切线斜率等于该曲线两个端点间的斜率之差。
为了更好地理解拉格朗日中值定理，我们可以通过一个具体的例子来说明。
假设有一个汽车在某段时间内行驶了一段距离，我们希望知道在这段时间内汽车的平均速度与某一刻的瞬时速度之间的关系。
根据拉格朗日中值定理，平均速度等于瞬时速度。
具体而言，在某一刻，汽车的瞬时速度等于汽车在该段时间内的总位移除以该段时间的长度，即平均速度。
拉格朗日中值定理的应用远不止于此，它可以用于证明很多重要的数学定理。
例如，利用拉格朗日中值定理，我们可以证明柯西中值定理、罗尔中值定理和费马定理等。
这些定理在微积分中具有重要的地位，并且被广泛应用于求解极值问题、证明函数的性质以及推导其他数学定理。
总之，高等数学拉格朗日中值定理是微积分中的一项基础且重要的定理。
通过该定理，我们可以了解函数在某个区间内的平均变化率与其导数在该区间内某点的值之间的关系。
此外，拉格朗日中值定理还可以用于证明其他重要的数学定理，为我们研究函数的性质和求解实际问题提供了有力的工具。
一拉格朗日中值定理拉格朗日中值定理，又被称为有限增量定理，是微积分中的一个基本定理。
拉格朗日中值公式的形式其实就是泰勒公式的一阶展开式的形式。
在现实应用当中，拉格朗日中值定有着很重要的作用。
拉格朗日中值定理是所有的微分中值定理当中使用最为普遍的定理。
拉格朗日中值定理的形成和发展过程都显示出了数学当中的一个定理的发展是一个推翻陈旧，出现创新的一个进程。
发现一些新的简单的定理去替代旧的复杂的定理，就是由初级走向高级。
用现代的语言来描述，在一个自变量x从x变为x+1的过程中，如果函数f(x)本身就是一个极限值，那么函数f(x+1)的值也应该是一个极限值，其值就应该和f(x)的值近似相等，即f(x+1)−f(x)≈01这就是非常著名的费马定律，当一个函数f(x)在x=a处可以取得极值，并且函数是可导函数，则f′(x)=0。
著名学者费马再给出上述定理时，此时的微积分研究理论正处于初始阶段，并没有很成熟的概念，没有对函数是否连续或者可导作出限制，因此在现代微积分理论成熟阶段这种说法就显得有些漏洞。
在所有的微分中值定理中，最重要的定理就是拉格朗日中值定理。
最初的拉格朗日中值定理和现在成熟的拉格朗日中值定理是不一样的，最初的定理是函数f(x)在闭区间[a,b]内任取两点x0和x1，并且函数f(x)在此闭区间内是连续的，f′(x)的最大值为A，f′(x)最小值为B，则f(x1)−f(x0)的值必须是A和B之间的一个x1−x0值。
这是拉格朗日定理最初的证明。
下述就是拉格朗日中值定理所要求满足的条件。
如果存在一个函数满足下面两个条件，（1）函数f 在闭区间[a，b]上连续；（2）函数f 在开区间（a，b）内可导；那么这个函数在此开区间内至少存在着.一点，使得f′(ξ)=f(b)−f(a)b−a拉格朗日中值定理是导数的一个延伸概念，在导数运算中是的很基本概念。
例1：函数f(x)=2x2−8，即f′(x)=4x。
当x在开区间(0,+∞)时，有f′(x) >0，f(x)在开区间(0,+∞)单调递增；当x在开区间(−∞,0)时，有f′(x)<0，f(x)在开区间(−∞,0)单调递减。
