拉格朗日中值定理
- 格式:doc
- 大小:642.00 KB
- 文档页数:9

一拉格朗日中值定理1.定理内容拉格朗日中值定理,又被称为有限增量定理,是微积分中的一个基本定理。
拉格朗日中值公式的形式其实就是泰勒公式的一阶展开式的形式。
在现实应用当中,拉格朗日中值定有着很重要的作用。
拉格朗日中值定理是所有的微分中值定理当中使用最为普遍的定理。
拉格朗日中值定理的形成和发展过程都显示出了数学当中的一个定理的发展是一个推翻陈旧,出现创新的一个进程。
发现一些新的简单的定理去替代旧的复杂的定理,就是由初级走向高级。
用现代的语言来描述,在一个自变量x从x变为x+1的过程中,如果函数f(x)本身就是一个极限值,那么函数f(x+1)的值也应该是一个极限值,其值就应该和f(x)的值近似相等,即这就是非常著名的费马定律,当一个函数在x=a处可以取得极值,并且函数是可导函数,则′。
著名学者费马再给出上述定理时,此时的微积分研究理论正处于初始阶段,并没有很成熟的概念,没有对函数是否连续或者可导作出限制,因此在现代微积分理论成熟阶段这种说法就显得有些漏洞。
在所有的微分中值定理中,最重要的定理就是拉格朗日中值定理。
最初的拉格朗日中值定理和现在成熟的拉格朗日中值定理是不一样的,最初的定理是函数f(x)在闭区间[a,b]内任取两点和,并且函数在此闭区间内是连续的,′的最大值为A,′最小值为B,则的值必须是A和B之间的一个值。
下述就是拉格朗日中值定理:如果存在一个函数满足下面两个条件,(1)函数f 在闭区间[a,b]上连续;(2)函数f 在开区间(a,b)内可导;那么这个函数在此开区间内至少存在着一点,使得′ξ.2.定理意义拉格朗日中值定理在数学的微积分属于重要的定理,是微分中值定理中应用最为广泛的定理,在发展过程中推算出了其他的微分中值定理,在实际应用中,具有重要的使用价值。
其中,拉格朗日中值定理在几何运算中所具有的意义是:若一个连续函数在两点、之间不存在垂直于x轴的切线,那么在这两点之间至少存在这一点,这一点的切线平行于直线AB。

拉格朗日中值定理————————————————————————————————作者: ————————————————————————————————日期:ﻩ拉格朗日中值定理引言众所周至拉格朗日中值定理是几个中值定理中最重要的一个,是微分学应用的桥梁,在高等数学的一些理论推导中起着很重要的作用. 研究拉格朗日中值定理的证明方法,力求正确地理解和掌握它,是十分必要的. 拉格朗日中值定理证明的关键在于引入适当的辅助函数. 实际上,能用来证明拉格朗日中值定理的辅助函数有无数个,因此如果以引入辅助函数的个数来计算,证明拉格朗日中值定理的方法可以说有无数个. 但事实上若从思想方法上分,我们仅发现五种引入辅助函数的方法. 首先对罗尔中值定理拉格朗日中值定理及其几何意义作一概述. 1罗尔()Rolle 中值定理如果函数()x f 满足条件:()1在闭区间[]b a ,上连续;()2在开区间()b a ,内可导;(3)()()b f a f =,则在()b a ,内至少存在一点ζ ,使得()0'=ζf罗尔中值定理的几何意义:如果连续光滑曲线()x f y =在点B A ,处的纵坐标相等,那么,在弧 ⋂AB 上至少有一点()(),Cf ζζ ,曲线在C 点的切线平行于x 轴,如图1,注意 定理中三个条件缺少其中任何一个,定理的结论将不一定成立;但不能认为定理条件不全具备,就一定不存在属于()b a ,的ζ,使得()0'=ζf . 这就是说定理的条件是充分的,但非必要的.2拉格朗日()lagrange 中值定理若函数()x f 满足如下条件:()1在闭区间[]b a ,上连续;()2在开区间()b a ,内可导;则在()b a ,内至少存在一点ζ,使()()()ab a f b f f--=ζ'拉格朗日中值定理的几何意义:函数()x f y =在区间[]b a ,上的图形是连续光滑曲线弧⋂AB 上至少有一点C ,曲线在C 点的切线平行于弦AB . 如图2,从拉格朗日中值定理的条件与结论可见,若()x f 在闭区间[]b a ,两端点的函数值相等,即()()b f a f =,则拉格朗日中值定理就是罗尔中值定理. 换句话说,罗尔中值定理是拉格朗日中值定理的一个特殊情形.正因为如此,我们只须对函数()x f 作适当变形,便可借助罗尔中值定理导出拉格朗日中值定理. 3 证明拉格朗日中值定理3.1 教材证法证明 作辅助函数 ()()()()f b f a F x f x x b a-=--显然,函数()x F 满足在闭区间[]b a ,上连续,在开区间()b a ,内可导,而且()()F a F b =.于是由罗尔中值定理知道,至少存在一点ζ()b a <<ζ,使()()()()0''=---=ab a f b f f F ζζ.即()()()ab a f b f f --=ζ'. 3.2 用作差法引入辅助函数法证明 作辅助函数 ()()()()()()⎥⎦⎤⎢⎣⎡---+-=a x a b a f b f a f x f x ϕ 显然,函数()x ϕ在闭区间[]b a ,上连续,在开区间()b a ,内可导,()()0==b a ϕϕ,因此,由罗尔中值定理得,至少存在一点()b a ,∈ζ,使得()()()()0''=---=ab a f b f f ζζϕ,即 ()()()ab a f b f f --=ζ'推广1 如图3过原点O 作OT ∥AB ,由()x f 与直线OT 对应的函数之差构成辅助函数()x ϕ,因为直线OT 的斜率与直线AB 的斜率相同,即有:()()ab a f b f K K AB OT --==,OT 的直线方程为:()()x ab a f b f y --=,于是引入的辅助函数为:()()()()x ab a f b f x f x ---=ϕ. (证明略)推广2 如图4过点()O a ,作直线''B A ∥AB ,直线''B A 的方程为:()()()a x ab a f b f y ---=,由()x f 与直线函''B A 数之差构成辅助函数()x ϕ,于是有:()()()()()a x ab a f b f x f x ----=ϕ. (证明略) 推广3 如图5过点作()O b ,直线''B A ∥AB ,直''B A 线的方程为()()()b x ab a f b f y ---=,由()x f 与直线A B ''函数之差构成辅助函数()x ϕ,于是有:()()()()()b x ab a f b f x f x ----=ϕ. 事实上,可过y 轴上任已知点()m O ,作//B A ∥AB 得直线为()()m x ab a f b f y +--=,从而利用()x f 与直线的''B A 函数之差构成满足罗尔中值定理的辅助函数()x ϕ都可以用来证明拉格朗日中值定理. 因m 是任意实数,显然,这样的辅助函数有无多个.3.3 用对称法引入辅助函数法在第二种方法中引入的无数个辅助函数中关于x 轴的对称函数也有无数个,显然这些函数也都可以用来证明拉格朗日中值定理.从几何意义上看,上面的辅助函数是用曲线函数()x f 减去直线函数,反过来,用直线函数减曲线函数()x f ,即可得与之对称的辅助函数如下:⑴ ()()()()()()x f a x a b a f b f a f x -⎥⎦⎤⎢⎣⎡---+=ϕ ⑵ ()()()()x f x ab a f b f x ---=ϕ⑶()()()()()x f a x a b a f b f x ----=ϕ ⑷ ()()()()()x f b x ab a f b f x ----=ϕ 等等.这类能用来证明拉格朗日中值定理的辅助函数显然也有无数个. 这里仅以⑵为例给出拉格朗日中值定理的证明.证明 显然,函数()x ϕ满足条件:()1在闭区间[]b a ,上连续;()2在开区间()b a ,内可导;()3()()()()ab a bf b af b a --==ϕϕ.由罗尔中值定理知,至少存在一点()b a ,∈ζ,使得()()()()0''=---=ζζϕf a b a f b f ,从而有()()()ab a f b f f --=ζ',显然可用其它辅助函数作类似的证明.3.4 转轴法由拉格朗日中值定理的几何图形可以看出,若把坐标系xoy 逆时针旋转适当的角度α,得新直角坐标系XOY ,若OX 平行于弦AB ,则在新的坐标系下()x f 满足罗尔中值定理,由此得拉格朗日中值定理的证明.证明 作转轴变换ααsin cos Y X x -=,ααcos sin Y X y +=,为求出α,解出Y X ,得()()x X x f x y x X =+=+=ααααsin cos sin cos ① ()()x Y x f x y x Y =+-=+-=ααααcos sin cos sin ② 由()()b Y a Y =得()()ααααcos sin cos sin b f b a f a +-=+-,从而()()ab a f b f --=αtan ,取α满足上式即可.由()x f 在闭区间[]b a ,上连续,在开区间()b a ,内可导,知()x Y 在闭区间[]b a ,上连续,在开区间()b a ,内可导,且()()b Y a Y =,因此,由罗尔中值定理知,至少存在一点()b a ,∈ζ,使得()()0cos sin '=+-=αζαζf Y ,即()()()ab a f b f f --==αζtan '3.5 用迭加法引入辅助函数法让()x f 迭加一个含待顶系数的一次函数m kx y +=,例如令()()()m kx x f x +-=ϕ或()()m kx x f x ++-=ϕ,通过使()()b a ϕϕ=,确定出m k ,,即可得到所需的辅助函数.例如由 ()()()m kx x f x +-=ϕ,令()()b a ϕϕ=得()()()()m kb b f m ka a f +-=+-,从而()()ab a f b f k --=,而m 可取任意实数,这样我们就得到了辅助函数()()()m x ab a f b f x ---=ϕ,由m 的任意性易知迭加法可构造出无数个辅助函数,这些函数都可用于证明拉格朗日中值定理.3.6 用行列式引入辅助函数法证明 构造一个含()x f 且满足罗尔中值定理的函数()x ϕ,关键是满足()()b a ϕϕ=.我们从行列式的性质想到行列式()()()111xf x af a bf b 的值在,x a x b ==时恰恰均为0,因此可设易证()()()()111xf x x af a bf b ϕ=,展开得 ()()()()()()()x f b x bf a af x af b f a x bf x ϕ=++---.因为()x f 在闭区间[]b a ,上连续,在开区间()b a ,内可导,所以()x ϕ在闭区间[]b a ,上连续,在开区间()b a ,内可导,且()()0a b ϕϕ==,所以由罗尔中值定理知,至少存在一点()b a ,∈ζ,使得()0'=ζϕ. 因为()()()()()0''=---=ζζϕf b a b f a f即: ()()()ab a f b f f --=ζ'3.7 数形相结合法引理 在平面直角坐标系中,已知ABC ∆三个顶点的坐标分别为()(),A a f a ,()(),B b f b ,()(),C c f c ,则ABC ∆面积为()()()1112ABCa f a Sb f b a cf c ∆=, 这一引理的证明在这里我们不做介绍,下面我们利用这一引理对拉格朗日中值定理作出一种新的证明. 这种方法是将数形相结合,考虑实际背景刻意构造函数使之满足罗尔中值定理的条件.如图, 设()(),c f c 是直线AB 与()y f x =从A 点开始的第一个交点,则构造()()()()211141af a x c f c xf x ϕ=, 易验证()x ϕ满足罗尔中值定理的条件:在闭区间[],a c 上连续,在开区间(),a c 内可导,而且()()b a ϕϕ=,则至少存在一点()b a ,∈ζ,使()/0ϕζ=,即:()()()()()()01111111'=ζζζf c f c a f a f c f ca f a但是()()()1101a f a cf c f ζζ≠,这是因为,如果 ()()()1101a f a c f c f ζζ=, 则()()()()f f c f c f a c c aζζ--=--,这样使得()(),f ζζ成为直线AB 与()y f x =从A 点的第一个交点,与已知矛盾).故()()()0111=ζζf c f ca f a,即()()()()()ac a f c f a b a f b f f --=--=ζ'. 若只从满足罗尔中值定理的要求出发,我们可以摈弃许多限制条件,完全可以构造()()()()111af a x bf b xf x ϕ=来解决问题,从而使形式更简洁,而且启发我们做进一步的推广:可构造()()()()()()()111g a f a x g b f b g x f x ϕ=来证明柯西中值定理.3.8 区间套定理证法证明 将区间[],I a b =二等分,设分点为1ζ,作直线1x ζ=,它与曲线()y f x = 相交于1M ,过1M 作直线11L M ∥弦b a M M . 此时,有如下两种可能:⑴ 若直线11M L 与曲线()y f x =仅有一个交点1M ,则曲线必在直线11M L 的一侧.否则,直线11M L 不平行于直线a b M M . 由于曲线()y f x =在点1M 处有切线,根据曲线上一点切线的定义,直线11M L 就是曲线()y f x =在点1M 处的切线,从而()()()ab a f b f f --=1ζ.由作法知,1ζ在区间(),a b 内部,取ζζ=1 于是有 ()()()ab a f b f f --=ζ ⑵ 若直线11M L 与曲线()y f x =还有除1M 外的其他交点,设()111,N x y 为另外一个交点,这时选取以11,x ξ为端点的区间,记作[]111,I a b =,有1,112b al I b a -⊇-<, ()()()()1111f b f a f b f a b a b a--=--,把1I 作为新的“选用区间”,将1I 二等分,并进行与上面同样的讨论,则要么得到所要求的点ζ,要么又得到一个新“选用区间”2I .如此下去,有且只有如下两种情形中的一种发生:(a) 在逐次等分“选用区间”的过程中,遇到某一个分点k ζ,作直线k x ζ=它与曲线()y f x =交于k M ,过点k M 作直线k k L M ∥弦b MM , 它与曲线()y f x =只有一个交点k M ,此时取ζζ=k 即为所求.(b ) 在逐次等分“选用区间”的过程中,遇不到上述那种点,则得一闭区间序列{n I },满足:① 12I I I ⊇⊇⊇ []n n n b a I ,=② ()02n n n b ab a n --<→→∞ ③()()()()n n n n f b f a f b f a b a b a--=-- 由①②知,{n I }构成区间套,根据区间套定理,存在唯一的一点() 3,2,1=∈n I n ζ,此点ζ即为所求. 事实上ζ==∞→∞→n n n n b a lim lim ,()fξ存在()()()ζf a b a f b f nn n n n =--∞→lim ,由③lim n →∞()()()()n n n n f b f a f b f a b a b a--=--,所以()()()a b a f b f f --=ζ,从“选用区间”的取法可知,ζ确在(),a b 的内部. 3.9 旋转变换法证明 引入坐标旋转变换A : cos sin x X Y αα=- ⑴ ααcos sin Y X y += ⑵ 因为 22cos sin cos sin 10sin cos αααααα-∆==+=≠所以A 有逆变换/A :()()cos sin cos sin X x y x f x X x αααα=+=+= ⑶()()sin cos sin cos Y x y x f x Y x αααα=-+=-+= ⑷ 由于()x f 满足条件: ()1在闭区间[]b a ,上连续;()2在开区间()b a ,内可导,因此⑷式中函数()Y x 在闭区间[]b a ,上连续,在开区间()b a ,内可导.为使()Y x 满足罗尔中值定理的第三个条件,只要适当选取旋转角α,使()()Y a Y b =,即()()sin cos sin cos a f a b f b αααα-+=-+,也即()()tan f b f a b aα-=-.这样,函数()Y x 就满足了罗尔中值定理的全部条件,从而至少存在一点()b a <<ζζ,使()()0cos sin =+=αζαζf Y 即()αζtan =f . 由于所选取旋转角α满足()()a b a f b f --=αtan ,所以()()()ab a f b f f --=ζ. 结论本论文仅是对拉格朗日中值定理的证明方法进行了一些归纳总结其中还有很多方法是我没有想到的,而且里面还有很多不足之处需要进一步的修改与补充. 通过这篇论文我只是想让人们明白数学并不是纯粹的数字游戏,里面包含了很多深奥的内容. 而且更重要的是我们应该学会去思考,学会凡是多问几个为什么,不要让自己仅仅局限于课本上的内容,要开动脑筋学会举一反三,不要单纯为了学习而学习,让自己做知识的主人!总之,数学的发展并非是无可置疑的,也并非是反驳的复杂过程,全面的思考问题有助于我们思维能力的提高,也有助于创新意识的培养.参考文献[1] 华东师范大学数学系. 数学分析(上册)(第二版)[M ].北京:高等教育出版社.1991:153-161[2] 吉林大学数学系. 数学分析(上册)[M].北京:人民教育出版社.1979:194-196[3] 同济大学应用数学系. 高等数学(第一册)[M].北京:高等教育出版社(第五版).2004:143-153[4] 周性伟,刘立民. 数学分析[M].天津:南开大学出版社.1986:113-124[5] 林源渠,方企勤. 数学分析解题指南[M ].北京:北京大学出版社.2003:58-67[6] 孙清华等. 数学分析内容、方法与技巧(上)[M].武汉:华中科技大学出版社.2003:98-106[7] 洪毅. 数学分析(上册)[M ].广州:华南理工大学出版社.2001:111-113[8] 党宇飞. 促使思维教学进入数学课堂的几点作法[J].上海:数学通报.2001,1:15-18[9] 王爱云. 高等数学课程建设和教学改革研究与实践[J].西安:数学通报.2002,2:84-88[10] 谢惠民等. 数学分析习题课讲义[M].北京:高等教育出版社.2003:126-135[11] 刘玉莲,杨奎元等. 数学分析讲义学习指导书(上册)[M].北京:高等教出版社.1994:98-112[12] 北京大学数学力学系. 高等代数. 北京:人民教育出版社. 1978:124-135[13] 裴礼文. 数学分析中的典型问题与方法[M].北京:高等教育出版社.1993:102-110[14] 郑琉信.数学方法论[M].南京:广西教育出版社.1996:112-123[15] 陈传璋等. 数学分析(上册)[M].北京:人民教育出版社.1983:87-92[16] 李成章,黄玉民. 数学分析(上)[M].北京:科学出版社.1995:77-86附 录柯西中值定理若 ⑴ 函数()f x 与()g x 都在闭区间[]b a ,上连续;⑵ ()x f'与()x g '在开区间()b a ,内可导; ⑶ ()x f ' 与()x g '在()b a ,内不同时为零;⑷ ()()g a g b ≠,则在()b a ,内至少存在一点ζ,使得()()()()a b a f b f g f --=ζζ''. 区间套定理若[]{},n n a b 是一个区间套,则存在唯一一点ζ,使得[],n n a b ζ∈,1,2,n = 或 n n a b ζ≤≤,1,2,n =。

拉格朗日中值定理的证明及应用证明拉格朗日中值定理:设函数f(x)在闭区间[a,b]上连续,且在开区间(a,b)内可导。
根据费尔马极值定理,f(x)在[a,b]的两个端点a和b处都有极值,或者f(x)在(a,b)内有临界点。
我们考虑临界点的情况,其他情况的证明思路类似。
若在(a,b)内,f'(c)=0,其中c为临界点。
那么根据定义,f'(c)=(f(b)-f(a))/(b-a)。
因此,f(b)-f(a)=0或者f'(c)=0(由于f(a)=f(b),我们得到f(b)-f(a)=0)。
当f(b)≠f(a)时,我们考虑函数f(x)在闭区间[a,b]上的最大值和最小值,设最大值为M,最小值为m。
根据最大值和最小值函数的定义,我们有m≤f(x)≤M,对于(a,b)内的所有x。
根据最大值和最小值定理,存在两个点x1和x2,使得f(x1)=M和f(x2)=m,并且这两个点都在开区间(a,b)内。
因此,我们有f(x2)-f(x1)=m-M,并且f'(c)=(f(x2)-f(x1))/(x2-x1)=(m-M)/(x2-x1)。
将这两个方程相连,我们得到了拉格朗日中值定理的公式形式:f'(c)=(f(b)-f(a))/(b-a)。
应用拉格朗日中值定理:1.导数为零的函数值相等的应用:根据拉格朗日中值定理,若f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,并且f'(c)=0,则f(x)在闭区间[a,b]上有一个临界点c,满足f(a)=f(b)。
2.函数的零点估计:假设f(x)在闭区间[a,b]上连续,并且在开区间(a,b)内可导。
若f(a)和f(b)异号且f(x)在该区间上不为零,那么根据拉格朗日中值定理,存在一个点c在开区间(a,b)内,使得f'(c)=(f(b)-f(a))/(b-a)=0。
这意味着在开区间(a,b)上存在一个零点。
3.应用于近似计算:通过拉格朗日中值定理,我们可以将一个复杂的函数在其中一点处的导数近似为该函数在该点与另一点之间的函数值之差除以两点之间的距离,即f'(c)≈(f(b)-f(a))/(b-a)。

拉格朗日中值定理条件拉格朗日(Lagrange)中值定理函数f(x)满足条件:(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导;拉格朗日中值定理又称拉氏定理,是微分学中的基本定理之一,它反映了可导函数在闭区间上的整体的平均变化率与区间内某点的局部变化率的关系。
拉格朗日法国数学家。
1754年开始研究数学,1766年接替了欧拉在柏林皇家科学院的职位,在那里工作达20年。
1786年去法国,先后担任巴黎高等师范学校和多科工艺学校教授。
他是18世纪仅次于欧拉的大数学家,工作涉及数论、代数方程论、微积分、微分方程、变分法、力学、天文学等许多领域。
在数学上,他最早的重要贡献是1759年解决了等周问题,从而开创了变分问题分析形式的一般解法。
1766~1787年是他科学研究的多产时期,1766~1773年,他在数论方面做了一系列研究,1766年证明了所谓佩尔(Pell)方程(x-Ay=1)的解的存在性,1770年证明费马的著名命题,每个正整数可表为至多4个平方数之和;1771年证明了著名的所谓威尔逊(Wilson)定理;1773年关于整数的型表示问题获得关键性成果。
1767~1777年,他又系统地研究了代数方程论,引入对称多项式理论,置换理论及预解式概念,指出根的排列理论是整个问题的真谛,对后来伽罗华的工作产生了重要影响。
在这期间,他还在微积分、微分方程、力学、天文学领域广泛开展研究,导致了他的两部不朽巨著《分析力学》(1788)、《微分原理中的解析函数论》(1797)。
著名的拉格朗日中值定理、拉格朗日余项、拉格朗日方程,对黎卡提方程的重要研究,对线性微分方程组的研究,对奇解与通解的联系的系统研究,都是这一时期的工作。
他也是最先试图为微积分提供严格基础的数学家之一,这使他成为实变函数论的先驱。
他还以在数学上追求简明与严格而被誉为第1个真正的分析学家。
拿破仑曾评价说:“拉格朗日是数学科学方面高耸的金字塔。

拉格朗日(Lagrange)中值定理
拉格朗日(Lagrange)中值定理是一个比较有用的数学定理,它的意思是:如果一个函数f在一个定义域内连续,在一个闭区间[a,b]上增加,那么在这一区间内至少存在一个数c,使得函数f在c处取得直线ab上f(a)和f(b)之间的中值。
拉格朗日中值定理的使用有很多,它的用处就在于它能够在较为复杂的问题中把许多复杂的计算简化,帮助我们快速找出求解结果。
比如,我们可以把积分运算归结为二阶多项式,再使用拉格朗日中值定理,从而把积分运算搞定,这样就可以把复杂的求积问题变成表达式计算,简单、快速。
此外,拉格朗日中值定理也被实际应用在非线性方程求解、曲线拟合、曲线分割以及高精度数值积分、极限的求解等等。
总的来说,拉格朗日中值定理的运用极其广泛,它在数学计算中也是有用的,可以大大减轻我们的计算量,为复杂的计算提供直接的解决方案。
拉格朗日中值定理
拉格朗日中值定理公式是f(b)-f(a)=f'(ξ)(b-a)(a<ξ<b)。
如果函数y=f(x)在闭区间a≤x≤b上连续且在开区间a≤x≤b上可微,那么在此区间内部至少存在一个中间值u,使得F(b)-f(a)/b-a=f(u).其中a<u<b2、多元函数中值定理不成立。
但存在拟微分平均值定理设D是一凸域,多元函数f(D)=Y。
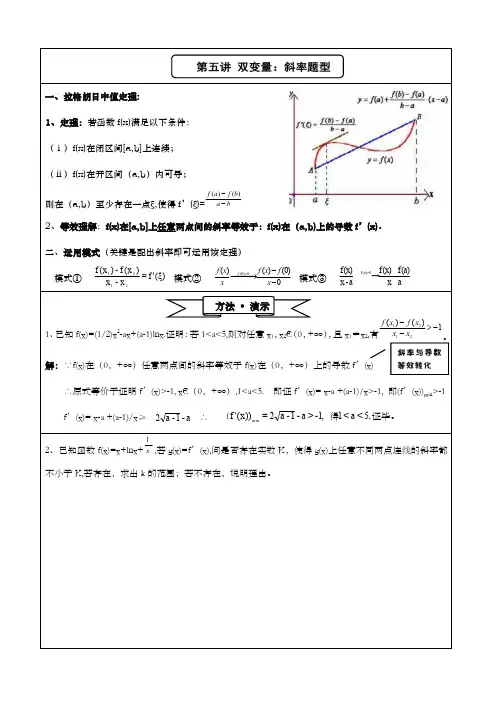
拉格朗日中值定理的几何意义
拉格朗日中值定理是微分中值定理的核心,其他中值定理是拉格朗日中值定理的特殊情况和推广,它是微分学应用的桥梁,在理论和实际中具有极高的研究价值。
其几何意义是若连续曲线在两点间的每一点处都有不垂直于x轴的切线,则曲线在A,B间至少存在1点,使得该曲线在P点的切线与割线AB平行。

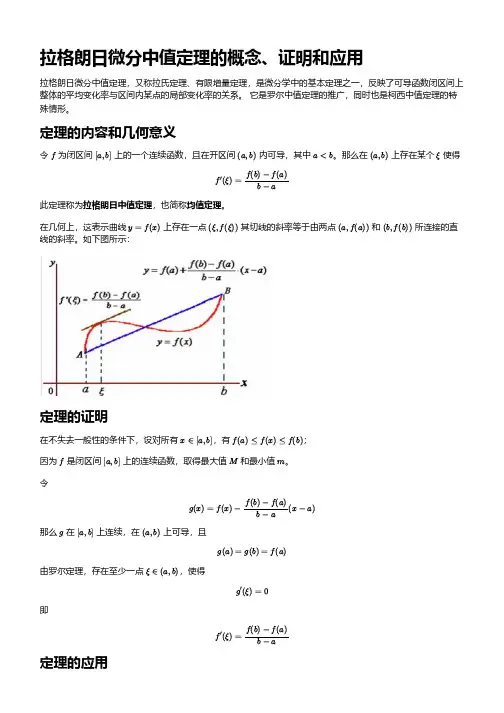
拉格朗日微分中值定理的概念、证明和应用拉格朗日微分中值定理,又称拉氏定理、有限增量定理,是微分学中的基本定理之一,反映了可导函数闭区间上整体的平均变化率与区间内某点的局部变化率的关系。
它是罗尔中值定理的推广,同时也是柯西中值定理的特殊情形。
定理的内容和几何意义令f为闭区间[a,b]上的一个连续函数,且在开区间(a,b)内可导,其中a<b。
那么在(a,b)上存在某个ξ使得f′(ξ)=f(b)−f(a)b−a此定理称为拉格朗日中值定理,也简称均值定理。
在几何上,这表示曲线y=f(x)上存在一点(ξ,f(ξ))其切线的斜率等于由两点(a,f(a))和(b,f(b))所连接的直线的斜率。
如下图所示:定理的证明在不失去一般性的条件下,设对所有x∈[a,b],有f(a)≤f(x)≤f(b);因为f是闭区间[a,b]上的连续函数,取得最大值M和最小值m。
令g(x)=f(x)−f(b)−f(a)b−a(x−a)那么g在[a,b]上连续,在(a,b)上可导,且g(a)=g(b)=f(a)由罗尔定理,存在至少一点ξ∈(a,b),使得g′(ξ)=0即f′(ξ)=f(b)−f(a)b−a定理的应用拉格朗日中值定理在微分学中有着广泛的应用,例如:证明函数单调性、极值、凹凸性等性质;估计函数误差、求函数极限、判断函数收敛性等问题;推导洛必达法则、泰勒公式、积分第一中值定理等重要结论。
下面举几个例子说明。
例1:证明函数单调性设f(x)在[a,b]上连续,在(a,b)内可导,且对任意x∈(a,b)有f′(x)>0,则f(x)在[a,b]上单调递增。
证明:任取x1,x2∈[a,b]且x1<x2,由拉格朗日中值定理,存在ξ∈(x1,x2)使得f′(ξ)=f(x2)−f(x1) x2−x1由于f′(ξ)>0且x2−x1>0,所以有f(x2)−f(x1)>0即f(x2)>f(x1)这说明f(x)在[a,b]上单调递增。

一拉格朗日中值定理拉格朗日中值定理,又被称为有限增量定理,是微积分中的一个基本定理。
拉格朗日中值公式的形式其实就是泰勒公式的一阶展开式的形式。
在现实应用当中,拉格朗日中值定有着很重要的作用。
拉格朗日中值定理是所有的微分中值定理当中使用最为普遍的定理。
拉格朗日中值定理的形成和发展过程都显示出了数学当中的一个定理的发展是一个推翻陈旧,出现创新的一个进程。
发现一些新的简单的定理去替代旧的复杂的定理,就是由初级走向高级。
用现代的语言来描述,在一个自变量x从x变为x+1的过程中,如果函数f(x)本身就是一个极限值,那么函数f(x+1)的值也应该是一个极限值,其值就应该和f(x)的值近似相等,即这就是非常著名的费马定律,当一个函数在x=a处可以取得极值,并且函数是可导函数,则′。
著名学者费马再给出上述定理时,此时的微积分研究理论正处于初始阶段,并没有很成熟的概念,没有对函数是否连续或者可导作出限制,因此在现代微积分理论成熟阶段这种说法就显得有些漏洞。
在所有的微分中值定理中,最重要的定理就是拉格朗日中值定理。
最初的拉格朗日中值定理和现在成熟的拉格朗日中值定理是不一样的,最初的定理是函数f(x)在闭区间[a,b]内任取两点和,并且函数在此闭区间内是连续的,′的最大值为A,′最小值为B,则的值必须是A和B之间的一个值。
这是拉格朗日定理最初的证明。
下述就是拉格朗日中值定理所要求满足的条件。
如果存在一个函数满足下面两个条件,(1)函数f 在闭区间[a,b]上连续;(2)函数f 在开区间(a,b)内可导;那么这个函数在此开区间内至少存在着一点,使得′ξ.拉格朗日中值定理是导数的一个延伸概念,在导数运算中是的很基本概念。
例1:函数,即′。
当在开区间∞时,有′,在开区间∞单调递增;当在开区间∞时,有′,f(x)在开区间∞单调递减。
在,有′,。
由上述例子说明,想要确定一个函数的单调性可以通过求得这个函数的一阶导数来求得判断单调区间。

拉格朗日中值定理的证明拉格朗日中值定理是微积分中的一个重要定理,它是关于函数在闭区间上的连续和可导条件下的一个性质。
拉格朗日中值定理的内容是:若函数f(x)在闭区间[a,b]上连续,在开区间(a,b)上可导,那么在(a,b)内至少存在一点ξ,使得f'(ξ) = [f(b) - f(a)] / (b - a)换句话说,对于函数f(x)在闭区间[a,b]上的任意两点a和b,至少存在一个介于a和b之间的点ξ,使得函数在这一点的导数等于函数在a和b之间的增量的平均斜率。
接下来我将给出拉格朗日中值定理的证明。
证明:由于f(x)在闭区间[a,b]上连续,在开区间(a,b)上可导,我们可以利用微分中值定理来证明拉格朗日中值定理。
首先我们定义一个新的函数F(x),使其满足F(x) = f(x) - [f(b) - f(a)] / (b - a) * (x - a)接下来我们来证明F(x)在闭区间[a,b]上满足罗尔定理的条件。
我们知道,罗尔定理要求函数在闭区间上连续,在开区间可导,并且在两个端点上取相同的函数值。
对于F(x)来说,显然它在闭区间上也是连续的,并且在开区间可导。
另外,F(a) = f(a) - [f(b) - f(a)] / (b - a) * (a - a) = f(a) - f(a) = 0,F(b) = f(b) - [f(b) -f(a)] / (b - a) * (b - a) = f(b) - f(a) = 0。
因此F(x)在闭区间[a,b]上满足罗尔定理的条件。
根据罗尔定理,存在一个ξ,使得F'(ξ) = 0。
接下来我们计算F'(x)。
由于F(x) = f(x) - [f(b) - f(a)] / (b - a) * (x - a),所以F'(x) = f'(x) - [f(b) - f(a)] / (b - a)。
然后根据罗尔定理,存在一个ξ,使得F'(ξ) = 0。
拉格朗日中值定理证明及其应用拉格朗日中值定理是微积分中的一个重要定理,可以帮助我们研究函数的性质和变化趋势。
它的证明基于连续函数的性质和导数的定义,下面我们来详细介绍该定理的证明及其应用。
拉格朗日中值定理的表述如下:设函数f在闭区间[a, b]上连续,在开区间(a, b)上可导,则在(a, b)内至少存在一个点c,使得f'(c) = (f(b)-f(a))/(b-a)。
证明:我们定义一个辅助函数g(x) = f(x) - ((f(b)-f(a))/(b-a))(x-a),则g(x)在闭区间[a, b]上连续,在开区间(a, b)上可导。
根据导数的定义,我们有g'(x) = f'(x) - ((f(b)-f(a))/(b-a))。
根据罗尔定理,若g(x)在闭区间[a, b]的两个端点值相等,则必存在一个点c,使得在(a, b)内g'(c) = 0。
根据g'(x)的定义,我们可以得到f'(c) - ((f(b)-f(a))/(b-a)) = 0,即f'(c) = (f(b)-f(a))/(b-a)。
所以根据罗尔定理,定理得证。
拉格朗日中值定理的应用非常广泛。
下面我们来介绍一些常见的应用场景。
1. 确定函数在某区间上的最值:通过拉格朗日中值定理,我们可以找到函数在某个区间上的最大值和最小值。
首先求出函数在该区间的导数,然后利用拉格朗日中值定理找到导数为零的点,再将这些点代入函数,即可得到最大值和最小值。
2. 研究函数的增减性:通过拉格朗日中值定理,我们可以找到函数在某个区间上的单调性。
若f'(x)>0,则函数在该区间上是增加的;若f'(x)<0,则函数在该区间上是减少的。
3. 证明函数的性质:拉格朗日中值定理可以帮助我们证明函数的某些性质。
对于严格单调函数,若在一个区间上导数恒大于零(或小于零),则函数在该区间上是严格递增(或递减)的。
一拉格朗日中值定理拉格朗日中值定理,又被称为有限增量定理,是微积分中的一个基本定理。
拉格朗日中值公式的形式其实就是泰勒公式的一阶展开式的形式。
在现实应用当中,拉格朗日中值定有着很重要的作用。
拉格朗日中值定理是所有的微分中值定理当中使用最为普遍的定理。
拉格朗日中值定理的形成和发展过程都显示出了数学当中的一个定理的发展是一个推翻陈旧,出现创新的一个进程。
发现一些新的简单的定理去替代旧的复杂的定理,就是由初级走向高级。
用现代的语言来描述,在一个自变量x从x变为x+1的过程中,如果函数f(x)本身就是一个极限值,那么函数f(x+1)的值也应该是一个极限值,其值就应该和f(x)的值近似相等,即这就是非常著名的费马定律,当一个函数在x=a处可以取得极值,并且函数是可导函数,则′。
著名学者费马再给出上述定理时,此时的微积分研究理论正处于初始阶段,并没有很成熟的概念,没有对函数是否连续或者可导作出限制,因此在现代微积分理论成熟阶段这种说法就显得有些漏洞。
在所有的微分中值定理中,最重要的定理就是拉格朗日中值定理。
最初的拉格朗日中值定理和现在成熟的拉格朗日中值定理是不一样的,最初的定理是函数f(x)在闭区间[a,b]内任取两点和,并且函数在此闭区间内是连续的,′的最大值为A,′最小值为B,则的值必须是A和B之间的一个值。
这是拉格朗日定理最初的证明。
下述就是拉格朗日中值定理所要求满足的条件。
如果存在一个函数满足下面两个条件,(1)函数f 在闭区间[a,b]上连续;(2)函数f 在开区间(a,b)内可导;那么这个函数在此开区间内至少存在着一点,使得′ξ.拉格朗日中值定理是导数的一个延伸概念,在导数运算中是的很基本概念。
例1:函数,即′。
当在开区间∞时,有′,在开区间∞单调递增;当在开区间∞时,有′,f(x)在开区间∞单调递减。
在,有′,。
由上述例子说明,想要确定一个函数的单调性可以通过求得这个函数的一阶导数来求得判断单调区间。
一拉格朗日中值定理拉格朗日中值定理,又被称为有限增量定理,是微积分中的一个基本定理。
拉格朗日中值公式的形式其实就是泰勒公式的一阶展开式的形式。
在现实应用当中,拉格朗日中值定有着很重要的作用。
拉格朗日中值定理是所有的微分中值定理当中使用最为普遍的定理。
拉格朗日中值定理的形成和发展过程都显示出了数学当中的一个定理的发展是一个推翻陈旧,出现创新的一个进程。
发现一些新的简单的定理去替代旧的复杂的定理,就是由初级走向高级。
用现代的语言来描述,在一个自变量x从x变为x+1的过程中,如果函数f(x)本身就是一个极限值,那么函数f(x+1)的值也应该是一个极限值,其值就应该和f(x)的值近似相等,即f(x+1)−f(x)≈01这就是非常著名的费马定律,当一个函数f(x)在x=a处可以取得极值,并且函数是可导函数,则f′(x)=0。
著名学者费马再给出上述定理时,此时的微积分研究理论正处于初始阶段,并没有很成熟的概念,没有对函数是否连续或者可导作出限制,因此在现代微积分理论成熟阶段这种说法就显得有些漏洞。
在所有的微分中值定理中,最重要的定理就是拉格朗日中值定理。
最初的拉格朗日中值定理和现在成熟的拉格朗日中值定理是不一样的,最初的定理是函数f(x)在闭区间[a,b]内任取两点x0和x1,并且函数f(x)在此闭区间内是连续的,f′(x)的最大值为A,f′(x)最小值为B,则f(x1)−f(x0)的值必须是A和B之间的一个x1−x0值。
这是拉格朗日定理最初的证明。
下述就是拉格朗日中值定理所要求满足的条件。
如果存在一个函数满足下面两个条件,(1)函数f 在闭区间[a,b]上连续;(2)函数f 在开区间(a,b)内可导;那么这个函数在此开区间内至少存在着.一点,使得f′(ξ)=f(b)−f(a)b−a拉格朗日中值定理是导数的一个延伸概念,在导数运算中是的很基本概念。
例1:函数f(x)=2x2−8,即f′(x)=4x。
当x在开区间(0,+∞)时,有f′(x) >0,f(x)在开区间(0,+∞)单调递增;当x在开区间(−∞,0)时,有f′(x)<0,f(x)在开区间(−∞,0)单调递减。
拉格朗日中值定理+
中值定理,也被称为拉格朗日中值定理,是一种有趣而重要的微积分学定理,
其最根本形式于18约1700年被拉格朗日研究发现,也是拉格朗日的有名的最优化原理之一。
该定理表明了函数的极值(最大值或最小值)是由三个样本点的内插值而来的,而不是两个或四个样本点。
即:如果一个连续函数f在闭区间[a,b]上具
有极值,若存在于区间[a,b]上的任意一个点c,满足f(a), f(b), f(c)就构成
一个凸的三角形的腰,那么函数f在定点c处就有极值,并且就是[a,b]区间内的
最大(或最小)值。
中值定理还与另一个有趣的事实有关,即“最小二乘法”,也叫拟合法。
借助
于这个方法,收集因变量和自变量变化的数据,可以用一条函数一致拟合它们。
那么,拟合函数的一个对称点就是拉格朗日中枢定理中所提到的c点。
这表明,非线性拟合中最小二乘法的优化结果是由拉格朗日中枢定理得出的。
从关键点包含许多的数学定义和推断中,我们可以看出,拉格朗日中值定理可
以引申出多种场景:比如,在经济学中,拉格朗日定理来自用计量经济学的最小二乘法拟合数据的示出;而在定理学和逻辑学领域,拉格朗日定理可以帮我们推断命题的真假性等;在几何学中,拉格朗日中值定理可以解释定点c位置到三角形三边的比例;以及更多其他领域中的应用。
拉格朗日中值定理是数学界一项关联丰富的重要定理,虽然用法和应用有限,
但其在一些研究领域中能帮助学者去解决一些问题或者实现一些想法,而这就是其存在的意义。
借助拉格朗日中枢定理,有效的把历史的遗产带进了今日的研究领域,加深我们对数学知识的了解,以及系统性、有效地利用数学工具解决实际问题的能力。
拉格朗日中值定理引言众所周至拉格朗日中值定理是几个中值定理中最重要的一个,是微分学应用的桥梁,在高等数学的一些理论推导中起着很重要的作用. 研究拉格朗日中值定理的证明方法,力求正确地理解和掌握它,是十分必要的. 拉格朗日中值定理证明的关键在于引入适当的辅助函数. 实际上,能用来证明拉格朗日中值定理的辅助函数有无数个,因此如果以引入辅助函数的个数来计算,证明拉格朗日中值定理的方法可以说有无数个. 但事实上若从思想方法上分,我们仅发现五种引入辅助函数的方法. 首先对罗尔中值定理拉格朗日中值定理及其几何意义作一概述. 1罗尔()Rolle 中值定理如果函数()x f 满足条件:()1在闭区间[]b a ,上连续;()2在开区间()b a ,可导;(3)()()b f a f =,则在()b a ,至少存在一点ζ ,使得()0'=ζf罗尔中值定理的几何意义:如果连续光滑曲线()x f y =在点B A ,处的纵坐标相等,那么,在弧 ⋂AB 上至少有一点()(),Cf ζζ ,曲线在C 点的切线平行于x 轴,如图1,注意 定理中三个条件缺少其中任何一个,定理的结论将不一定成立;但不能认为定理条件不全具备,就一定不存在属于()b a ,的ζ,使得()0'=ζf . 这就是说定理的条件是充分的,但非必要的.2拉格朗日()lagrange 中值定理若函数()x f 满足如下条件:()1在闭区间[]b a ,上连续;()2在开区间()b a ,可导;则在()b a ,至少存在一点ζ,使()()()ab a f b f f--=ζ'拉格朗日中值定理的几何意义:函数()x f y =在区间[]b a ,上的图形是连续光滑曲线弧⋂AB 上至少有一点C ,曲线在C 点的切线平行于弦AB . 如图2,从拉格朗日中值定理的条件与结论可见,若()x f 在闭区间[]b a ,两端点的函数值相等,即()()b f a f =,则拉格朗日中值定理就是罗尔中值定理. 换句话说,罗尔中值定理是拉格朗日中值定理的一个特殊情形.正因为如此,我们只须对函数()x f 作适当变形,便可借助罗尔中值定理导出拉格朗日中值定理. 3 证明拉格朗日中值定理3.1 教材证法证明 作辅助函数 ()()()()f b f a F x f x x b a-=--显然,函数()x F 满足在闭区间[]b a ,上连续,在开区间()b a ,可导,而且()()F a F b =.于是由罗尔中值定理知道,至少存在一点ζ()b a <<ζ,使()()()()0''=---=ab a f b f f F ζζ.即()()()ab a f b f f --=ζ'.3.2 用作差法引入辅助函数法证明 作辅助函数 ()()()()()()⎥⎦⎤⎢⎣⎡---+-=a x a b a f b f a f x f x ϕ 显然,函数()x ϕ在闭区间[]b a ,上连续,在开区间()b a ,可导,()()0==b a ϕϕ,因此,由罗尔中值定理得,至少存在一点()b a ,∈ζ,使得()()()()0''=---=ab a f b f f ζζϕ,即 ()()()ab a f b f f --=ζ'推广1 如图3过原点O 作OT ∥AB ,由()x f 与直线OT 对应的函数之差构成辅助函数()x ϕ,因为直线OT 的斜率与直线AB 的斜率相同,即有:()()ab a f b f K K AB OT --==,OT 的直线方程为:()()x ab a f b f y --=,于是引入的辅助函数为:()()()()x ab a f b f x f x ---=ϕ. (证明略)推广2 如图4过点()O a ,作直线''B A ∥AB ,直线''B A 的方程为:()()()a x ab a f b f y ---=,由()x f 与直线函''B A 数之差构成辅助函数()x ϕ,于是有:()()()()()a x ab a f b f x f x ----=ϕ. (证明略) 推广3 如图5过点作()O b ,直线''B A ∥AB ,直''B A 线的方程为()()()b x ab a f b f y ---=,由()x f 与直线A B ''函数之差构成辅助函数()x ϕ,于是有:()()()()()b x ab a f b f x f x ----=ϕ. 事实上,可过y 轴上任已知点()m O ,作//B A ∥AB 得直线为()()m x ab a f b f y +--=,从而利用()x f 与直线的''B A 函数之差构成满足罗尔中值定理的辅助函数()x ϕ都可以用来证明拉格朗日中值定理. 因m 是任意实数,显然,这样的辅助函数有无多个.3.3 用对称法引入辅助函数法在第二种方法中引入的无数个辅助函数中关于x 轴的对称函数也有无数个,显然这些函数也都可以用来证明拉格朗日中值定理.从几何意义上看,上面的辅助函数是用曲线函数()x f 减去直线函数,反过来,用直线函数减曲线函数()x f ,即可得与之对称的辅助函数如下:⑴ ()()()()()()x f a x a b a f b f a f x -⎥⎦⎤⎢⎣⎡---+=ϕ ⑵ ()()()()x f x ab a f b f x ---=ϕ⑶ ()()()()()x f a x a b a f b f x ----=ϕ ⑷ ()()()()()x f b x ab a f b f x ----=ϕ 等等.这类能用来证明拉格朗日中值定理的辅助函数显然也有无数个. 这里仅以⑵为例给出拉格朗日中值定理的证明.证明 显然,函数()x ϕ满足条件:()1在闭区间[]b a ,上连续;()2在开区间()b a ,可导;()3()()()()ab a bf b af b a --==ϕϕ.由罗尔中值定理知,至少存在一点()b a ,∈ζ,使得()()()()0''=---=ζζϕf a b a f b f ,从而有()()()ab a f b f f --=ζ',显然可用其它辅助函数作类似的证明.3.4 转轴法由拉格朗日中值定理的几何图形可以看出,若把坐标系xoy 逆时针旋转适当的角度α,得新直角坐标系XOY ,若OX 平行于弦AB ,则在新的坐标系下()x f 满足罗尔中值定理,由此得拉格朗日中值定理的证明.证明 作转轴变换ααsin cos Y X x -=,ααcos sin Y X y +=,为求出α,解出Y X ,得()()x X x f x y x X =+=+=ααααsin cos sin cos ① ()()x Y x f x y x Y =+-=+-=ααααcos sin cos sin ② 由()()b Y a Y =得()()ααααcos sin cos sin b f b a f a +-=+-,从而()()ab a f b f --=αtan ,取α满足上式即可.由()x f 在闭区间[]b a ,上连续,在开区间()b a ,可导,知()x Y 在闭区间[]b a ,上连续,在开区间()b a ,可导,且()()b Y a Y =,因此,由罗尔中值定理知,至少存在一点()b a ,∈ζ,使得()()0cos sin '=+-=αζαζf Y ,即()()()ab a f b f f --==αζtan ' 3.5 用迭加法引入辅助函数法让()x f 迭加一个含待顶系数的一次函数m kx y +=,例如令()()()m kx x f x +-=ϕ或()()m kx x f x ++-=ϕ,通过使()()b a ϕϕ=,确定出m k ,,即可得到所需的辅助函数.例如由 ()()()m kx x f x +-=ϕ,令()()b a ϕϕ=得()()()()m kb b f m ka a f +-=+-,从而()()ab a f b f k --=,而m 可取任意实数,这样我们就得到了辅助函数()()()m x ab a f b f x ---=ϕ,由m 的任意性易知迭加法可构造出无数个辅助函数,这些函数都可用于证明拉格朗日中值定理.3.6 用行列式引入辅助函数法证明 构造一个含()x f 且满足罗尔中值定理的函数()x ϕ,关键是满足()()b a ϕϕ=.我们从行列式的性质想到行列式()()()111xf x af a bf b 的值在,x a x b ==时恰恰均为0,因此可设易证()()()()111xf x x af a bf b ϕ=,展开得 ()()()()()()()x f b x bf a af x af b f a x bf x ϕ=++---.因为()x f 在闭区间[]b a ,上连续,在开区间()b a ,可导,所以()x ϕ在闭区间[]b a ,上连续,在开区间()b a ,可导,且()()0a b ϕϕ==,所以由罗尔中值定理知,至少存在一点()b a ,∈ζ,使得()0'=ζϕ. 因为()()()()()0''=---=ζζϕf b a b f a f即: ()()()ab a f b f f --=ζ'3.7 数形相结合法引理 在平面直角坐标系中,已知ABC ∆三个顶点的坐标分别为()(),A a f a ,()(),B b f b ,()(),C c f c ,则ABC ∆面积为()()()1112ABCa f a Sb f b a cf c ∆=, 这一引理的证明在这里我们不做介绍,下面我们利用这一引理对拉格朗日中值定理作出一种新的证明. 这种方法是将数形相结合,考虑实际背景刻意构造函数使之满足罗尔中值定理的条件.如图, 设()(),c f c 是直线AB 与()y f x =从A 点开始的第一个交点,则构造()()()()211141af a x c f c xf x ϕ=, 易验证()x ϕ满足罗尔中值定理的条件:在闭区间[],a c 上连续,在开区间(),a c 可导,而且()()b a ϕϕ=,则至少存在一点()b a ,∈ζ,使()/0ϕζ=,即:()()()()()()01111111'=ζζζf c f c a f a f c f ca f a但是()()()1101a f a cf c f ζζ≠,这是因为,如果 ()()()1101a f a c f c f ζζ=, 则()()()()f f c f c f a c c aζζ--=--,这样使得()(),f ζζ成为直线AB 与()y f x =从A 点的第一个交点,与已知矛盾).故()()()0111=ζζf c f ca f a,即()()()()()ac a f c f a b a f b f f --=--=ζ'. 若只从满足罗尔中值定理的要求出发,我们可以摈弃许多限制条件,完全可以构造()()()()111af a x bf b xf x ϕ=来解决问题,从而使形式更简洁,而且启发我们做进一步的推广:可构造()()()()()()()111g a f a x g b f b g x f x ϕ=来证明柯西中值定理. 3.8 区间套定理证法证明 将区间[],I a b =二等分,设分点为1ζ,作直线1x ζ=,它与曲线()y f x = 相交于1M ,过1M 作直线11L M ∥弦b a M M . 此时,有如下两种可能:⑴ 若直线11M L 与曲线()y f x =仅有一个交点1M ,则曲线必在直线11M L 的一侧.否则,直线11M L 不平行于直线a b M M . 由于曲线()y f x =在点1M 处有切线,根据曲线上一点切线的定义,直线11M L 就是曲线()y f x =在点1M 处的切线,从而()()()ab a f b f f --=1ζ.由作法知,1ζ在区间(),a b 部,取ζζ=1 于是有 ()()()ab a f b f f --=ζ ⑵ 若直线11M L 与曲线()y f x =还有除1M 外的其他交点,设()111,N x y 为另外一个交点,这时选取以11,x ξ为端点的区间,记作[]111,I a b =,有1,112b al I b a -⊇-<, ()()()()1111f b f a f b f a b a b a--=--,把1I 作为新的“选用区间”,将1I 二等分,并进行与上面同样的讨论,则要么得到所要求的点ζ,要么又得到一个新“选用区间”2I .如此下去,有且只有如下两种情形中的一种发生:(a) 在逐次等分“选用区间”的过程中,遇到某一个分点k ζ,作直线k x ζ=它与曲线()y f x =交于k M ,过点k M 作直线k k L M ∥弦b MM , 它与曲线()y f x =只有一个交点k M ,此时取ζζ=k 即为所求.(b) 在逐次等分“选用区间”的过程中,遇不到上述那种点,则得一闭区间序列{n I },满足:① 12I I I ⊇⊇⊇ []n n n b a I ,=② ()02n n n b ab a n --<→→∞ ③()()()()n n n n f b f a f b f a b a b a--=-- 由①②知,{n I }构成区间套,根据区间套定理,存在唯一的一点() 3,2,1=∈n I n ζ,此点ζ即为所求. 事实上ζ==∞→∞→n n n n b a lim lim ,()fξ存在()()()ζf a b a f b f nn n n n =--∞→lim ,由③lim n →∞()()()()n n n n f b f a f b f a b a b a--=--,所以()()()a b a f b f f --=ζ,从“选用区间”的取法可知,ζ确在(),a b 的部. 3.9 旋转变换法证明 引入坐标旋转变换A : cos sin x X Y αα=- ⑴ ααcos sin Y X y += ⑵因为 22cos sin cos sin 10sin cos αααααα-∆==+=≠所以A 有逆变换/A :()()cos sin cos sin X x y x f x X x αααα=+=+= ⑶()()sin cos sin cos Y x y x f x Y x αααα=-+=-+= ⑷ 由于()x f 满足条件: ()1在闭区间[]b a ,上连续;()2在开区间()b a ,可导,因此⑷式中函数()Y x 在闭区间[]b a ,上连续,在开区间()b a ,可导.为使()Y x 满足罗尔中值定理的第三个条件,只要适当选取旋转角α,使()()Y a Y b =, 即()()sin cos sin cos a f a b f b αααα-+=-+,也即()()tan f b f a b aα-=-.这样,函数()Y x 就满足了罗尔中值定理的全部条件,从而至少存在一点()b a <<ζζ,使()()0cos sin =+=αζαζf Y 即()αζtan =f . 由于所选取旋转角α满足()()a b a f b f --=αtan ,所以()()()ab a f b f f --=ζ. 结论本论文仅是对拉格朗日中值定理的证明方法进行了一些归纳总结其中还有很多方法是我没有想到的,而且里面还有很多不足之处需要进一步的修改与补充. 通过这篇论文我只是想让人们明白数学并不是纯粹的数字游戏,里面包含了很多深奥的容. 而且更重要的是我们应该学会去思考,学会凡是多问几个为什么,不要让自己仅仅局限于课本上的容,要开动脑筋学会举一反三,不要单纯为了学习而学习,让自己做知识的主人!总之,数学的发展并非是无可置疑的,也并非是反驳的复杂过程,全面的思考问题有助于我们思维能力的提高,也有助于创新意识的培养.参考文献[1] 华东师大学数学系. 数学分析(上册)(第二版)[M].:高等教育.1991:153-161 [2] 大学数学系. 数学分析(上册)[M].:人民教育.1979:194-196[3] 同济大学应用数学系. 高等数学(第一册)[M].:高等教育(第五版).2004:143-153 [4] 周性伟,立民. 数学分析[M].天津:南开大学.1986:113-124 [5] 林源渠,方企勤. 数学分析解题指南[M].:大学.2003:58-67[6] 清华等. 数学分析容、方法与技巧(上)[M].:华中科技大学.2003:98-106[7] 洪毅. 数学分析(上册)[M].:华南理工大学.2001:111-113[8] 党宇飞. 促使思维教学进入数学课堂的几点作法[J].:数学通报.2001,1:15-18 [9] 王爱云. 高等数学课程建设和教学改革研究与实践[J].:数学通报.2002,2:84-88 [10] 惠民等. 数学分析习题课讲义[M].:高等教育.2003:126-135[11] 玉莲,奎元等. 数学分析讲义学习指导书(上册)[M].:高等教.1994:98-112 [12] 大学数学力学系. 高等代数. :人民教育. 1978:124-135[13] 裴礼文. 数学分析中的典型问题与方法[M].:高等教育.1993:102-110 [14] 琉信.数学方法论[M].:广西教育.1996:112-123 [15] 传璋等. 数学分析(上册)[M].:人民教育.1983:87-92 [16] 成章,黄玉民. 数学分析(上)[M].:科学.1995:77-86附 录柯西中值定理若 ⑴ 函数()f x 与()g x 都在闭区间[]b a ,上连续; ⑵ ()x f '与()x g '在开区间()b a ,可导;⑶ ()x f' 与()x g '在()b a ,不同时为零;⑷ ()()g a g b ≠,则在()b a ,至少存在一点ζ,使得()()()()a b a f b f g f --=ζζ''. 区间套定理若[]{},n n a b 是一个区间套,则存在唯一一点ζ,使得 [],n n a b ζ∈,1,2,n = 或 n n a b ζ≤≤,1,2,n =。