概率统计实验12多准则决策问题Word版
- 格式:doc
- 大小:388.50 KB
- 文档页数:9

概率统计学中的随机决策问题学院:数学科学学院年级:***专业:数学与应用数学姓名:***学号:***指导教师:***摘要至今,概率论与数理统计的理论与方法已广泛应用于自然科学、社会科学及人文科学等各个领域中,并且随着计算机的普及,概率论与数理统计已成为处理信息、制定决策的重要理论与方法。
本文就以“概率统计学中的随机决策问题”为题,结合现实情况,运用概率论与数理统计的理论知识来解决与人们生活密切相关的问题,以地震预测和大学生择业两个问题为主要内容,解决问题,得出结论。
关键词概率论,数理统计,决策,地震预测。
AbstractSo far, Probability theory and mathematical statistics theory and method has been widely used in Natural Science、Social and Human Sciences in the fields, and with the popularization of computers, probability theory and mathematical statistics has become to deal with information, an important decision-making theory and method.This article on "statistical probability of a random decision-making" as the title, combined with the actual situation, the use of probability theory and mathematical statistics, theory of knowledge to solve people's lives and is closely related to the problem of earthquake prediction and college students to careers as the main two issues content, solve problems, reach a conclusion.KeywordsProbability theory, mathematical statistics, decision-making, earthquake prediction.目录摘要 (I)ABSTRACT (II)第一章综述 (1)第二章地震预测 (3)3.1地震基本概念 (3)3.2震级分布 (3)3.1最大震级分布 (4)第三章大学毕业生职场择业决策依据与风险分析 (7)3.1择业决策依据分析 (7)3.2择业决策风险分析 (9)第四章概率中的数学游戏 (12)结论 (13)参考文献 (14)致谢 (15)第一章综述数理统计是随机数学的重要分支,它是基于观测数据来研究随机现象,研究如何有效的收集、整理和分析带有随机性的数据,以对所观察的问题做出推测和预测,直至为采取一定的决策和行动提供依据和建议,数理统计是以概率为基础的。

统计与概率中的决策问题第一类 回归分析中的“决策”【例1】(2018·莆田3月教学质量检测)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:吨)和年利润z (单位:千元)的影响,对近13年的年宣传费x i 和年销售量y i (i =1,2,…,13)数据作了初步处理,得到如图2311所示的散点图及一些统计量的值.图2311由散点图知,按y =a +b x ,y =c +dx 建立y 关于x 的回归方程是合理的.令s =x ,t =1x , 经计算得如下数据:x y s t 10.15109.943.040.16∑13i =1s i y i-13s y ∑13i =1t i y i-13t y ∑13i =1s 2i -13s 2 ∑13i =1t 2i -13t 2∑13i =1y 2i -13y 213.94-2.1011.67 0.21 21.22i i i i 12(1)从以上模型中选择更优的回归方程,并用相关系数加以说明; (2)根据(1)的选择结果及表中数据,建立y 关于x 的回归方程;(3)已知这种产品的年利润z 与x ,y 的关系为z =10y -x .根据(2)的结果回答下列问题: (ⅰ)年宣传费x =20时,年利润的预报值是多少? (ⅱ)年宣传费x 为何值时,年利润的预报值最大? 附:对于一组数据()()()1122,,,,,,n n u v u v u v ,其回归直线v u βα=⋅+中的斜率和截距的最小二乘估计分别为()()()1221,n i ii ni i u v n uv v u u n u βαβ==-==-⋅-∑∑【解析】 (1)由于|r 1|<|r 2|<1,故y =c +dx 更优.(2)=∑13i =1t i y i-13t y ∑13i =1t 2i -13t 2=-2.100.21=-10,=y -t =109.94+10×0.16=111.54.则y 关于x 的回归方程为=111.54-10x .(3)由题意,年利润z =10y -x =1 115.4-⎝ ⎛⎭⎪⎫100x +x ,(ⅰ)当x =20时,年利润的预报值是=1 115.4-⎝ ⎛⎭⎪⎫10020+20=1 090.4.(ⅱ)由基本不等式得,年利润的预报值=1 115.4-⎝ ⎛⎭⎪⎫100x +x ≤1 115.4-2100x ×x =1095.4,当且仅当x =10时等号成立,故年宣传费x 为10时,年利润的预报值最大.【例2】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:万元)对年销售量y (单位:吨)和年利润z (单位:万元)的影响。
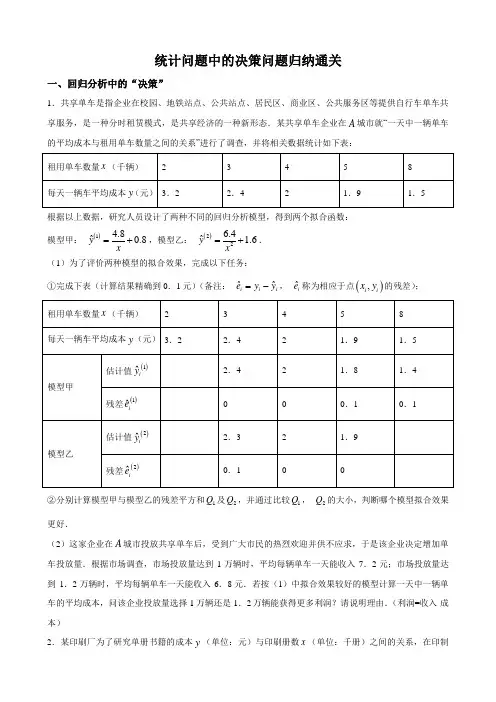
统计问题中的决策问题归纳通关一、回归分析中的“决策”1.共享单车是指企业在校园、地铁站点、公共站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是一种分时租赁模式,是共享经济的一种新形态.某共享单车企业在A 城市就“一天中一辆单车的平均成本与租用单车数量之间的关系”进行了调查,并将相关数据统计如下表:根据以上数据,研究人员设计了两种不同的回归分析模型,得到两个拟合函数:模型甲: ()1 4.8.8ˆ0yx =+,模型乙: ()226.4.ˆ16yx=+. (1)为了评价两种模型的拟合效果,完成以下任务:①完成下表(计算结果精确到0.1元)(备注: ˆˆi i i e y y =-, ˆi e 称为相应于点(),i i x y 的残差);②分别计算模型甲与模型乙的残差平方和1Q 及2Q ,并通过比较1Q , 2Q 的大小,判断哪个模型拟合效果更好.(2)这家企业在A 城市投放共享单车后,受到广大市民的热烈欢迎并供不应求,于是该企业决定增加单车投放量.根据市场调查,市场投放量达到1万辆时,平均每辆单车一天能收入7.2元;市场投放量达到1.2万辆时,平均每辆单车一天能收入6.8元.若按(1)中拟合效果较好的模型计算一天中一辆单车的平均成本,问该企业投放量选择1万辆还是1.2万辆能获得更多利润?请说明理由.(利润=收入-成本)2.某印刷厂为了研究单册书籍的成本y (单位:元)与印刷册数x (单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲: ()141.1ˆyx=+,方程乙: ()226.4.ˆ16yx=+. (1)为了评价两种模型的拟合效果,完成以下任务. ①完成下表(计算结果精确到0.1);②分别计算模型甲与模型乙的残差平方和1Q 及2Q ,并通过比较12,Q Q 的大小,判断哪个模型拟合效果更好.(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷,根据市场调查,新需求量为10千册,若印刷厂以每册5元的价格将书籍出售给订货商,求印刷厂二次印刷10千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).3.在2017年初的时候,国家政府工作报告明确提出,2017年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少,6月至11月的用煤量如下表所示:(1)由于某些原因, y 中一个数据丢失,但根据6至9月份的数据得出少样本平均值是3.5,求出丢失的数据;(2)请根据6至9月份的数据,求出y 关于x 的线性回归方程ˆˆˆybx a =+; (3)现在用(2)中得到的线性回归方程中得到的估计数据与10月11月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过0.3,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?(参考公式:线性回归方程ˆˆˆybx a =+,其中()()()1122211ˆn ni i i i i i n n i i i i x x y y x y nxy b x x x nx====---==--∑∑∑∑) 4.某地区某农产品近几年的产量统计如下表:(1)根据表中数据,建立y 关于x 的线性回归方程ˆˆˆybt a =+; (2)若近几年该农产品每千克的价格v (单位:元)与年产量y 满足的函数关系式为 4.50.3v y =-,且每年该农产品都能售完.①根据(1)中所建立的回归方程预测该地区()20187t =年该农产品的产量; ②当()17t t ≤≤为何值时,销售额S 最大? 附:对于一组数据()()()1122,,,,,,n n t y t y t y ,其回归直线ˆˆˆybt a =+的斜率和截距的最小二乘估计分别为: ()()()121ˆni i i n i i t t y y b t t ==--=-∑∑, ˆˆa y bt =-. 5.某基地蔬菜大棚采用水培、无土栽培方式种植各类蔬菜.过去50周的资料显示,该地周光照量X (小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量y (百斤)与使用某种液体肥料x (千克)之间对应数据为如图所示的折线图.(1)依据数据的折线图,是否可用线性回归模型拟合y 与x 的关系?请计算相关系数r 并加以说明(精确到0.01).(若0.75r >,则线性相关程度很高,可用线性回归模型拟合)(2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪最多可运行台数受周光照量X 限制,并有如下关系: 周光照量X (单位:小时) 3050X <<5070X ≤≤70X >光照控制仪最多可运行台数321若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.若商家安装了3台光照控制仪,求商家在过去50周周总利润的平均值.附:相关系数公式()()()()12211niii nniii i x x y y r x x y y ===--=--∑∑∑,参考数据0.30.55≈,.6.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费(单位:万元)对年销售量(单位:吨)和年利润(单位:万元)的影响。

实验十二 多准则决策问题一 实验目的通过用层次分析法解决一个多准则决策问题, 学习层次分析法的基本原理与方法; 掌握用层次分析法建立数学模型的基本步骤;学会用Mathematica 解决层次分析法中的数学问题.二 学习Mathematica 命令有时在计算中只需求出实数解, 而省略复数解, 则可以输入调用只求实数解的软件包. 输入<<Miscellaneous\RealOnly.m即可.三 实验的基本原理与方法层次分析法是一种简便、灵活而实用的多准则决策方法. 它特别适用于难以完全定量进行分析的,又相互关联、相互制约的众多因素构成的复杂问题. 它把人的思维过程层次化、数量化, 是系统分析的一个新型的数学方法.运用层次分析法建模,大体上可分四个基本步骤进行:1. 建立层次结构首先对所面临的问题要掌握足够的信息. 搞清楚问题的范围、因素、各因素之间的相互关系,及所要解决问题的目标. 把问题条理化、层次化,构造出一个有层次的结构模型. 在这个模型下,复杂问题被分解为元素的组成部分. 这些元素又按其属性及关系形成若干层次. 层次结构一般分三类:第一类为最高层,它是分析问题的预定目标和结果,也称目标层;第二类为中间层,它是为了实现目标所涉及的中间环节,如:准则、子准则,也称准则层;第三类为最低层,它包括了为实现目标可供选择的各种措施、决策方案等,也称方案层. OO 的影响之比,全部比较的结果可用矩阵表示,n n ij==⨯矩阵称为判断矩阵. 定义1 若判断矩阵满足下列条件:则称判断矩阵A 为正互反矩阵.怎样确定判断矩阵A 的元素ij a 取值?当某层的元素n C C C ,,,21 对于上一层某元素O 的影响可直接定量表示时(如利润多少),i C 与j C 对O 的影响之比可以直接确定,ij a 的值也易得到.但对于大多数社会经济问题,特别是比较复杂的问题,元素i C 和j C 对O的重要性不容易直接获得,需要通过适当的方法解决.通常取数字1-9及其倒数作为ij a 的取值范围.这是因为在进行定性的成对比较时,人们头脑中通常有5个明显的等级:因素太多,将超出人们的判断比较能力,降低精确. 实践证明,成对比较的尺度以72±为宜. 故ij a 的取值范围是1,2,9, 及其倒数1,.91,,21 3. 计算层次单排序并做一致性检验层次单排序是指同一层次各个元素对于上一层次中的某个元素的相对重要性进行排序. 具体做法是:根据同一层n 个元素n C C C ,,,21 ,对上一层某元素O 的判断矩阵A 求出它们对于元素O 的相对排序权重,记为:n w w w ,,,21 .写成向量形式:()T n w w w w ,,,21 = ,称为A 的排序权重向量. 其中i w 表示第i 个元素对上一层中某元素O 所占的比重. 从而得到层次单排序.层次单排序权重向量可有几种方法求解,常用的方法是利用判断矩阵A 的特征值与特征向量来计算排序权重向量w .为此引出矩阵的特征值与特征向量的有关理论.定义2 如果一个正互反矩阵().,,2,1,,n j i a A nn ij ==⨯满足 ),,2,1,,(n k j i a a a ik jk ij ==⨯,则称矩阵A 具有一致性,称元素k j i c c c ,,的成对比较是一致的; 并且称A 为一致矩阵.根据矩阵理论,可以得到如下几个定理.定理1 n 阶正互反矩阵A 的最大特征根m ax λn ≥,当n =λ时,A 是一致的.定理2 n 阶正互反矩阵是一致矩阵的充分必要条件是最大特征值m ax λn =.计算排序权重向量方法和步骤:设()T n w w w w ,,,21 =是n 阶判断矩阵的排序权重向量,当A 为一致矩阵时,根据n 阶判断矩阵构成的意义,显然有⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n n n n n n w w w w w w w w w w w w w w w w w w A 212221212111 (1) 因而满足 nw Aw =. 这里n 是矩阵A 的最大特征根,w 是相应的特征向量;当A 为一般的判断矩阵时w Aw max λ=. 其中m ax λ是A 的最大特征值(也称主特征根),w 是相应的特征向量(也称主特征向量). 经归一化后(即:∑==n i i w11),可近似作为排序权重向量,这种方法称为特征根法.一致性检验:在判断矩阵的构造中,并没有要求判断矩阵具有一致性的特点. 这是由于客观事物的复杂性与人的认识的多样性所决定.特别是在规模大、因素多的情况下,对于判断矩阵的每个元素来说,不可能求出精确的ji w w .但要求判断矩阵大体上应该是一致的. 一个经不起推敲的判断矩阵有可能导致决策的失误. 利用上述方法计算排序权向量,当判断矩阵过于偏离一致性时,其可靠程度也出现问题. 因此需要对判断矩阵的一致性进行检验. 其步骤如下:(1)计算一致性指标..I C1..max --=n nI C λ (2)当0..=I C 时,即n =max λ时,判断矩阵A 是一致的.当..I C 值越大,判断矩阵A 的不一致的程度越严重.(2)查找相应的平均随机一致性指标..I R下表给出了n (从1—11)阶正互反矩阵,用了100—150个随机样本矩阵A 算出的随机一致性指标..I R......I R I C R C = (3) 当10.0..<R C 时,认为判断矩阵的一致性是可以接受的,否则应对判断矩阵作适当修正.4. 计算层次总排序权重并做一致性检验在得到了某层元素对其上一层中某元素的排序权重向量后,还需要得到各层元素,特别是最低层中各方案对于目标层的排序权重,即层次总排序权重向量,从而进行方案选择. 层次总排序权重要自上而下地将层次单排序的权重进行合成得到.考虑3个层次的决策问题. 若第一层只有1个元素,第二层有n 个元素,第三层有m 个元素,设第二层对第一层的层次单排序的权重向量为:第三层对第二层的层次单排序的权重为:以)3(k w 为列向量构成矩阵 ()nm nm m m n n n w w w w w w w w w w w w W ⨯⎪⎪⎪⎪⎪⎭⎫ ⎝⎛==)3()3(2)3(1)3(2)3(22)3(12)3(1)3(21)3(11)3()3(2)3(1)3(,,,(4) 则第三层对第一层的层次总排序权重向量为)2()3()3(w W w = (5)一般地,若有s 层,则第k 层对第一层的总排序权重向量为s k w W w k k k ,,4,3,)1()()( ==- (6)其中)(k W 是以第k 层对第k-1层的排序权向量为列向量组成的矩阵,)1(-k w 是第k-1层对第一层的总排序权重向量. 按照上述递推公式,可得到最下层(第s 层)对第一层的总排序权重向量为 )2()3()1()()(w W W W w s s s -= (7)层次总排序权重向量也要进行一致性检验. 具体方法是从最高层到最低层逐层进行. 定义3:若考虑的决策问题共有s 层. 设第l (s l ≤≤3)层的一致性指标为)1(.,,.,.)()(2)(1层元素的数目是第-l n I C I C I C l n l l ; 第l 层的随机一致性指标为 )()(2)(1.,,.,.l n l l I R I R I R ,令)1()(1)(1)(].,,.[.-=l l l l w I C I C I C (8))1()(1)(1)(].,,.[.-=l l l l w I R I R I R (9)则第l 层对第一层的总排序权向量的一致性比率为s l I R I C R C RC l l l l ,,4,3,....)()()1()( =+=-. (10) 其中)2(.R C 为由(3)式计算的第二层对第一层的排序权向量的一致性比率. 当最下层对第一层的总排序权向量的一致性比率1.0.)(<s RC 时,认为整个层次结构的比较判断可通过一致性检验.。



实践课:概率计算与决策11.1随机事件的概率(复习)奉港高级中学 杨亢尔教学目的1、复习本节知识要点,进一步了解随机事件概率和等可能事件概率的意义;23 师:12 我们把一次试验连同其中可能出现的每一个结果称为一个基本事件,如果一次试验中可能出现的结果有n 个,即此试验有n 个基本事件组成,而且所有出现的可能性都相等,那么每一个基本事件的概率都是n 1。
如果某个事件A 包含的结果有m 个,那么事件A 的概率nm A P =)(,显然1)(0≤≤A P 。
3.从集合的角度看等可能事件的概率在一次试验中,如果等可能出现的结果有n 个,我们把这n 个结果看成n 个元素组成的集合I ,包含m 个结果的事件A 对应于I 中含有m 个元素的子集A ,若分别用)(I card 和)(A card 表示I 和A 中的元素个数,则nm I card A card A P ==)()()(。
师:本节内容概念较多,能否掌握好本节内容,关系到高中概率和统计内容的学习。
我们在学习中不能只背条文,必须在理解上下工夫,加深对随机事件概率和等可能事件概率的意义的理解和应用。
我们来看下面的问题:脑,生生 生这样选择的理由。
师:这位同学不轻信自己的直觉,敢于怀疑,这种理性思维方式难能可贵!生3:我觉得应该改变选择,换到另一扇未打开的门。
师:事实上,你的选择是正确的!众生:啊?!师:能把你的想法跟同学们说说吗?生3:我是这样考虑的,首先把门编上号,1号门,2号门和3号门。
假设最初选择的是3号门,在主持人打开一扇有铅笔的门后,如果仍旧坚持原来的选择,那么只有一种情况能获得手提电脑,即3号门后是手提电脑。
而我们如果改变选择转移到另一扇门,那么只要手提电脑不在3号门后,就会获奖,即当2号门或1号门后是手提电脑时,有两种情况会获奖。
由此,改变选择会使获得手提电脑的概率大一倍,所以我认为应该改变原来的选择。
众生:哇!原来如此!师:从大家的赞叹声中可以看出,改变原来的选择实在是一种明智之举。

【关键字】条件高中数学第一章统计案例 1.2.1 条件概率与独立事件同步测控北师大版选修1-2我夯基我达标1.两人同时向一敌机射击,甲的命中率为,乙的命中率为,则两人中恰有一人击中敌机的概率是…( )A. B. C. D.解析:甲、乙击中敌机分别记作事件A、B,则P=P(A+B)=P(A)+P(B)=P(A)P()+P()P(B)=×(1)+(1)×=.答案:A2.某人一周晚上值班2次,在已知他星期日一定值班的前提下,则他在其余晚上值班所占的概率为( )A. B. C. D.解析:本题为条件概率,在星期日一定值班的前提下,只需再从其余6天中选一天值班即可,概率为.答案:D3.一个口袋内装有大小相等的5个白球和3个黑球,从中任取出两个球,在第一次取出是黑球的前提下,第二次取出黑球的概率为( )A. B. C. D.解析:设第一次取出黑球为事件A,第二次取出黑球为事件B,则P(A)=,P(AB)=,∴P(B|A)=.答案:D4.三个运动员打破纪录的概率都是0.1,一次比赛中记录未能打破的概率是( ).1-0.9解析:三个运动员打破纪录分别为事件A、B、C,则P(A)=P(B)=P(C)=0.1,则未打破纪录的概率为P=P()=P()P()P()=(1-0.1)3=0.93.答案:A5.从一副不含大小王的52张扑克牌中,不放回地抽取3次,每次抽1张,已知前两次抽到K,则第三次抽到A的概率是( )A. B. C. D.解析:前两次抽到K,第三次抽到A的概率为.答案:C6.甲口袋内装有大小相等的8个红球和4个白球,乙口袋内装有大小相等的9个红球和3个白球,从两个口袋内各摸出一球,那么等于( )A.2个球都是白球的概率B.2个球中恰好有1个是白球的概率C.2个球都不是白球的概率D.2个球不都是红球的概率解析:2个球都是白球的概率为×=;2个球恰好有1个是白球的概率为×+×=.答案:B7.一种零件的加工由两道工序组成,第一道工序的废品率为p,第二道工序的废品率为q,则该零件加工成品率为___________.解析:两道工序都不能为废品,即概率为(1-p)(1-q).答案:(1-p)(1-q)8.盒中有10只螺丝钉,其中3只是坏的,现从盒中随机抽取2只,那么在第一只抽取为好的的前提下,至多1只是坏的的概率是___________.解析:第一只抽取好螺丝钉为事件A,则第二次抽取至多1只是坏的有两种可能,①抽取好的,②抽取坏的,即抽取好的、坏的都满足要求,概率为1.答案:1我综合 我发展9.一道数学难题,学生甲能解出它的概率为,学生乙能解出它的概率为,学生丙能解出它的概率为,则甲、乙、丙三人独立解答此题时恰有一人解出此题的概率是___________.解析:设学生甲、乙、丙能解出此题分别为事件A 、B 、C 它们相互独立,则P(A)=,P(B)= ,P(C)=,则P()=,P()=,P()=,∴恰有一人解出此题的概率为P(A+B+C)=P(A)+P(B)+P(C)=P(A)P()P()+P()P(B)P()+P()P()P(C)=××+××+××=.答案:10.某市派出甲、乙两支球队分别参加全省青年组,少年组足球赛,甲、乙两队夺冠的概率分别为和,则该市足球队夺取冠军的概率是_____________.解析:设甲夺冠为事件A,乙夺冠为事件B,则A 、B 相互独立.该市夺冠为事件A+B+AB 概率为P(A+B+AB)=P(A)P()+P()P(B)+P(A)P(B)=×+×+×=或1-P()=1-P()P()=1×=.答案:11.盒中有20只灯泡,其中5只是坏的,现从盒中随机抽取3只,已知抽取一只是坏的,问再抽取两只好的的概率是多少?解析:可直接计算,也可用条件概率公式计算.解:P=.12.袋中有大小相同的4个红球和6个白球,每次从中摸取一球,每个球被取到的可能性相同,现不放回地取3个球.(1)求第三次取出红球的概率;(2)在已知前两次取出的是白球的前提下,第三次取出红球的概率.解析:(1)无条件概率按古典概型计算,(2)为条件概率.解:设第三次取出红球为事件A,前两次取出白球为事件B.(1)由于每次取到红球的概率相等,所以第三次取出红球的概率就等于第一次取出红球的概率P(A)=104=52,(2)P(B)=3121026=C C ,P(AB)=613101423=A A A , ∴P(A|B)=213161)()(==B P AB P . 13.设两个独立事件A 和B 都不发生的概率为91,A 发生B 不发生的概率与B 发生A 不发生的概率相同,则A 发生的前提下B 发生的概率是多少?解析:本题为相互独立事件的概率及条件概率的综合问题,可根据公式进行运算. 解:由已知P(A B )=91,P(A B )=P(B A ),即P(A)P(B )=P(B)P(A ),即P(A)[1-P(B)]=P(B)[1-P(A)],∴P(A)-P(A)P(B)=P(B)-P(A)P(B).∴P(A)=P(B). ∴P(A )=P(B )=31. ∴P(A)=32,P(B)=32,P(AB)=P(A)P(B)=94. ∴P(B|A)=3294)()(=A P AB P =32. 14.甲、乙两人独立地破译1个密码,他们能译出密码的概率分别为31和41, 求:(1)两人都译出密码的概率;(2)两人都译不出密码的概率;(3)恰有1人译出密码的概率;(4)至多有1人译出密码的概率.解析:本题为相互独立事件同时发生的概率,“至多”“至少”可正面计算,也可反面排除.解:设甲、乙译出密码分别记作事件A 、B,则P(A)=31,P(B)=41,P(A )=32,P(B )=43. (1)两人都译出密码的概率P(AB)=P(A)P(B)=31×41=121. (2)两人都译不出密码的概率P(A B )=P(A )P(B )=32×43=21. (3)恰有一人译出密码的概率为P(A B +A B)=P(A)P(B )+P(A )P(B)=31×43+32×41=41+61= 125或1-P(AB)-P(A B )=112521121=--. (4)至多有1人译出密码的概率为P(A B )+P(A B +A B)=21+125=1211或1-P(AB)=1121-=1211. 我创新 我超越15.掷三颗骰子,试求:(1)没有一颗骰子出现1点或6点的概率;(2)恰好一颗骰子出现1点或6点的概率.解析:三颗骰子出现1点或6点是相互独立的,其对立事件也是相互独立的,恰好一颗骰子出现1点或6点对应三种可能.解:设三颗骰子出现1点或6点分别依次记作事件A,事件B,事件C,则P(A)=P(B)=P(C)=31,P(A )=P(B )=P(C )=32, 则没有一颗骰子出现1点或6点的概率为P(A B C )=P(A )P(B )P(C )=278,恰好一颗骰子出现1点或6点的概率为P(A B C +A B C +A B C)=P(A B C )+P(A B C )+ P(A B C)=P(A)P(B )P(C )+P(A )P(B)P(C )+P(A )P(B )P(C)=3×31×(32)2=94. 16.某种电路开关闭合后,会出现红灯或绿灯闪动,已知开关第一次闭合后,出现红灯和出现绿灯的概率都是21,从开关第二次闭合起,若前次出现红灯,则下次出现红灯的概率是31,出现绿灯的概率是32,若前次出现绿灯,则下次出现红灯的概率是23,出现绿灯的概率是52,问:(1)第二次闭合后出现红灯的概率是多少?(2)三次发光后,出现一次红灯、两次绿灯的概率是多少?解析:本题各种情况较为复杂,可一一列举出来.解:(1)如果第一次出现红灯,则接着又出现红灯记为事件A,则P(A)=21×31=61, 如果第一次出现绿灯,则接着又出现红灯记为事件B,则P(B)=21×53=103. 所以第二次出现红灯的概率为P(A+B)=P(A)+P(B)=61+103=157. (2)由题意,三次发光后,出现一次红灯、两次绿灯的情况共有如下3种方式: ①出现绿、绿、红时的概率为21×52×53=253; ②出现绿、红、绿时概率为21×53×32=51; ③出现红、绿、绿时概率为21×32×52=152; ∴三次发光后,出现一次红灯、两次绿灯的概率为253+51+152=7534.此文档是由网络收集并进行重新排版整理.word 可编辑版本!。

统计与概率中的决策问题第一类 回归分析中的“决策”【例1】(2018·莆田3月教学质量检测)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:吨)和年利润z (单位:千元)的影响,对近13年的年宣传费x i 和年销售量y i (i =1,2,…,13)数据作了初步处理,得到如图2311所示的散点图及一些统计量的值.图2311由散点图知,按y =a +b x ,y =c +d x 建立y 关于x 的回归方程是合理的.令s =x ,t =1x , 经计算得如下数据:x y s t 10.15109.943.040.16∑13i =1s i y i -13s y ∑13i =1t i y i-13t y ∑13i =1s 2i -13s 2∑13i =1t 2i -13t 2∑13i =1y 2i -13y 213.94 -2.10 11.67 0.21 21.22i i i i 12(1)从以上模型中选择更优的回归方程,并用相关系数加以说明; (2)根据(1)的选择结果及表中数据,建立y 关于x 的回归方程;(3)已知这种产品的年利润z 与x ,y 的关系为z =10y -x .根据(2)的结果回答下列问题: (ⅰ)年宣传费x =20时,年利润的预报值是多少? (ⅱ)年宣传费x 为何值时,年利润的预报值最大?附:对于一组数据()()()1122,,,,,,n n u v u v u v L ,其回归直线v u βα=⋅+中的斜率和截距的最小二乘估计分别为()()()1221,ni i i ni i u v n uv v u u n u βαβ==-==-⋅-∑∑【例2】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:万元)对年销售量y (单位:吨)和年利润z (单位:万元)的影响。
对近六年的年宣传费i x 和年销售量)6,5,4,3,2,1(=i y i 的数据作了初步统计,得到如下数据: 年份2011 2012 2013 2014 2015 2016 年宣传费x (万元) 38 48 58 68 78 88 年销售量y (吨)16.818.820.722.424.025.5经电脑模拟,发现年宣传费x (万元)与年销售量y (吨)之间近似满足关系式(,0),b y a x a b =⋅>即。

试卷一一、填空(每小题2分,共10分)1.设是三个随机事件,则至少发生两个可表示为______________________。
2. 掷一颗骰子,表示“出现奇数点”,表示“点数不大于3”,则表示______________________。
3.已知互斥的两个事件满足,则___________。
4.设为两个随机事件,,,则___________。
5.设是三个随机事件,,,、,则至少发生一个的概率为___________。
二、单项选择(每小题的四个选项中只有一个是正确答案,请将正确答案的番号填在括号内。
每小题2分,共20分)1. 从装有2只红球,2只白球的袋中任取两球,记“取到2只白球”,则()。
(A) 取到2只红球(B) 取到1只白球(C) 没有取到白球(D) 至少取到1只红球2.对掷一枚硬币的试验, “出现正面”称为()。
(A) 随机事件(B) 必然事件(C) 不可能事件(D) 样本空间3. 设A、B为随机事件,则()。
(A) A (B) B(C) AB(D) φ4. 设和是任意两个概率不为零的互斥事件,则下列结论中肯定正确的是()。
(A) 与互斥(B) 与不互斥(C) (D)5. 设为两随机事件,且,则下列式子正确的是()。
(A) (B)(C) (D)6. 设相互独立,则()。
(A) (B)(C) (D)7.设是三个随机事件,且有,则()。
(A) 0.1 (B) 0.6(C) 0.8 (D) 0.78. 进行一系列独立的试验,每次试验成功的概率为p,则在成功2次之前已经失败3次的概率为()。
(A) p2(1–p)3 (B) 4 p (1–p)3(C) 5 p2(1–p)3(D) 4 p2(1–p)39. 设A、B为两随机事件,且,则下列式子正确的是()。
(A) (B)(C) (D)10. 设事件A与B同时发生时,事件C一定发生,则()。
(A) P(A B) = P (C) (B) P (A) + P (B) –P (C) ≤1(C) P (A) + P (B) –P (C) ≥1 (D) P (A) + P (B) ≤P (C)三、计算与应用题(每小题8分,共64分)1. 袋中装有5个白球,3个黑球。

预测:根据过去和现在估计未来,预测未来统计预测:用科学的统计方法对事物的未来发展进行定量推测,并计算概率置信区间统计预测三要素:实际资料是依据,经济理论是基础,数学模型是手段影响预测的因素:费用的高低,预测方法的难易程度,预测结果的精确程度按预测方法分类:(1)定性预测法:通过预测者所掌握的信息结合各种因素对事物的发展前景做出判断,并将判断定量化(2)回归预测法:研究变量与变量之间相互关系的数理统计方法,从一个值或几个自变量的值去预测因变量的值(3)时间序列预测法:考虑变量随时间变化发展规律并用该变量以往的统计资料简历数学模型做外推按预测时间分类:近期预测,短期预测,中期预测,长期预测预测方法的选择:考虑合适性、费用和精确性各种预测方法特点:(1)定性预测法:短期、中期、长期,适用于对缺乏历史统计资料或趋势面临转折的事件进行预测,需做大量的调查研究工作(2)一元线性回归预测法:短期、中期,适用于自变量与因变量两个变量之间存在着线性关系,需为两个变量收集历史数据(3)多元线性回归预测法:短期、中期,适用于因变量与两个或两个以上自变量之间存在着线性关系,需为所有变量收集历史数据(4)非线性回归预测法:短期、中期,适用于因变量与一个或多个自变量之间存在某种非线性关系,必须收集历史数据,并用几个非线性模型实验(5)趋势外推法:中期、长期,适用于当被预测项目的有关变量用时间表示时,用非线性回归,只需要因变量的历史数据,但用趋势图试探是费时统计预测研究步骤:(1)确定预测目的(2)搜集和审核资料(3)选择预测模型和方法(4)分析预测误差、改进预测模型(5)提出预测报告定性预测的优缺点:优点在于注重事物发展在性质方面的预测,具有较大的灵活性,易于充分发挥人的主观能动作用,且简单迅速,省时、省费用;缺点在于易受主观因素影响,比较注重人的经验和主观判断能力,从而易受人的知识、经验和能力的多少大小的束缚和限制,尤其缺乏对事物发展做数量上的精确描述定量预测的优缺点:优点在于注重事物发展在数量方面的分析,重视对事物发展变化的程度做数量上的描述,更多的依据历史统计资料,较少受主观因素的影响,可以利用电子计算机对统计发放和数学方法做大量计算处理;缺点在于比较机械,不以灵活掌握,对信息资料的质量和数量要求较高,且不易处理有较大波动的信息资料,更难以预测事物质的变化德尔菲法的特点:(1)反馈性:表现在多次作业、反复、综合、整理、归纳和修正,但不是漫无边际,而是有组织有步骤的进行(2)匿名性:免除心理干扰影响(3)统计性:对各位专家的估计或预测数进行统计,然后采用平均数或中位数统计出量化结果德尔菲法的优缺点:优点在于(1)加快预测速度,节约预测费用(2)获得各种不同但有价值的观点和意见(3)适用于长期预测和对新产品的预测,在历史资料不足或不可测因素较多时尤为适用缺点在于(1)对于分地区的顾客群或产品的预测可能不可靠(2)责任比较分散(3)专家的意见有时可能不完整或不切合实际厂长(经理)评判意见法优缺点:优点在于:(1)迅速、及时和经济(2)发挥集体智慧,是预测结果比较准确可靠(3)不需要大量统计资料,更适用于不可控因素较多的产品进行销售预测(4)市场发生变化时可以立即修正缺点在于:(1)结果用一首主观因素影响(2)对市场变化、顾客愿望等问题了解不细,预测结果一般化估计量要求:好的估计量满足一致性、无偏性和有效性.定性分析注意事项:在运用时注意它的作用与范围,超过这个范围去推断或预测,可能会得到错误结论.直线回归适用范围:只适宜做中、短期预测,不宜于做长期预测关于对数据资料的要求问题:(1)关于数据资料的准确性问题(2)关于数据资料的可比性和独立性问题(3)关于社会经济现象基本稳定的问题正确应用回归分析方法注意事项:(1)用定性分析判断现象之间的依存关系(2)避免回归预测的任意外推(3)应用合适的数据资料长期趋势因素(T):反映了经济现象在一个较长时间内的发展方向,在一个相当长的时间内表现为一种近似直线的持续向上或持续向下或平稳的趋势,也可以表现为类似指数趋势或其它曲线趋势的形式。
常见大题:1. 全概率公式和贝叶斯公式问题 B 看做“结果〞,有多个“原因或者条件iA 〞可以导致B 这个“结果〞发生,考虑结果B 发生的概率,或者求在B 发生的条件下,源于某个原因iA 的概率问题全概率公式:()()()1B |ni i i P B P A P A ==∑贝叶斯公式:1(|)()()()()ni i i jjj P A B P A P B A P A P BA ==∑||一〔12分〕今有四个口袋,它们是甲、乙、丙、丁,每个口袋中都装有a 只红球和b 只白球。
先从甲口袋中任取一只球放入乙口袋,再从乙口袋中任取一只球放入丙口袋,然后再从丙口袋中任取一只球放入丁口袋,最后从丁口袋中任取一球,问取到红球的概率为多少? 解 i B 表示从第i 个口袋放入第1+i 个口袋红球,4,3,2,1=ii A 表示从第i 个口袋中任取一个球为红球, 2分那么ba aB P +=)(1, 2分 )()()()()(1111111B A P B P B A P B P A P += 111++++++++=b a a b a b b a a b a a b a a+= 2分依次类推 2分ba a A P i +=)( 二〔10分〕袋中装有m 只正品硬币,n 只次品硬币〔次品硬币的两面均印有国徽〕,在袋中任取一只,将它投掷r 次,每次都出现国徽,问这只硬币是次品的概率为多少?、解记B ={取到次品},B ={取到正品},A ={将硬币投掷r 次每次都出现国徽} 那么()(),n m P B P B m n m n==++,()1P A B =,()12r P A B =―—5分 ()()1()212()()()()12r r r nP B P A B n m n P B A n m n m P B P A B P B P A B m n m n ⨯+===++⨯+⨯++三、〔10分〕一批产品共100件,其中有4件次品,其余皆为正品。
•多准则决策问题:指在具有相互冲突、不可共度的有限(无限)方案集中进行选择的决策。
•解决方法:
①把评价标准1,评价标准2……,评价标准n归纳为一个新的评价标准,即综合评价
标准。
然后使其最大化为决策标准进行最优决策。
综合评价标准=评价标准1的重要系数x评价标准1+评价标准2的重要系数x评价标准2……+评价标准n的重要系数x评价标准n
②除评价标准1以外的所有评价标准都视为约束条件,也就说评价标准2到n分别取
可妥协的最小值,只有评价标准1为最大化。
•决策行为:评价标准最大化
•评价标准:评价标准1
•制约条件:原有制约条件以外,
评价标准2〉可妥协最小值2
评价标准3〉可妥协最小值3
……
评价标准n〉可妥协最小值n
•通过以上俩种方法可以使原本复杂的问题归结为生产者最优决策的基本原理来进行分析,并作出判断和决策。
生产者最优决策的基本原理:
评价标准的边际值=0时的生产量为最适生产量。
概率统计在风险决策中的应用05级数学系四班王世钇摘要:近几年来,我国的经济学界和经济部门越来越意识到用数学方法来解决经济问题的重要性,正在探索经济问题中应有数学的规律。
实践证明,概率统计是对经济和经济管理问题进行量的研究的有效工具,为经济预测和决策提供了新的手段,有助于提高管理水平和经济效益。
本文将利用概率统计方法解决一些经济问题,分析研究怎样进行风险决策以及怎样检验产品质量和确定产品进货量等。
关键词:概率统计;经济问题;风险决策目录第一章概率与风险决策 (1)1.1 引言 ................................... . (2)1.2 风险决策中的应用........................................................5.1.2.1 先验信息决策分析......................................................9.1.2.2 后验信息决策分析......................................................12..第二章概率与保险..............................................................2.1 概率与保险................................................................. 第三章概率与人寿保险问题.....................................................3.1 概率与人寿保险问题......................................................... 第四章小结...................................................................4.1 小结....................................................................... 参考文献.......................................................................第一章概率与风险决策1.1引言随着我国经济建设的发展,在企业管理工作中的人们越来越重视经济分析的数量化,管理和决策的科学化,这就使数理统计理论与方法逐步渗透到管理科学的各个领域,且其重要性已为人们所公认。
第5章多目标决策分析习题参考解答5-1对于单层次、多层次序列型和多层次非序列型三种目标准则体系,各举出一个社会生活或经济管理的实例,并构造目标准则体系的结构图。
参考解答:单层次目标体系(设备采购)系列型多层次目标准则体系(课题立项选择)总人口非系列型多层次目标准则体系(某地区总人口)5-2对学生进行综合评价的目标准则体系、效用并合规则和权系数如图5-36所示,用多2 1 2 15-3某个工厂有一百多个岗位,这些岗位复杂程度各不相同,工作的环境各不一样,一个合理的岗位丁资分配制度对于提高员工满意度、体现人力资源的公平性具有非常重要的作用,而该工厂所处的行业比较特殊,没有可以借鉴的经验,必须由该工厂对自已的岗位工资水平进行合理地定义。
现已知社会的平均丁资水平,该公司决定比社会平均工资水平高10% 做为公司总的基数,工厂面临的问题是如何对工厂内部各个岗位的工资基数进行分配?以一线员工的岗位工资为例,在对公司各层次的调查中,大家一致同意将劳动强度、岗 位技术含量、生产出的产品对质量的影响以及该岗位员工的获得性做为一个评判标准。
(1) 劳动强度:越高则工资应该越高; (2) 技术含量:越高则工资应该越高; (3) 对质量影响:影响越大则工资应该越高; (4) 工人获得性:越难获得的岗位,工资应该越高。
以A 、B 、C 、D 四个岗位为例,利用层次分析法进行分析求出这四个岗位的薪酬水平应该 怎样分配才是合理的,在这里A 、B 、C 、D 是我们要分析的决策变量。
参考解答:首先,选择四个岗位,我们以研发、采购、生产、销售四个岗位为例,来分 析该厂的薪酬分配问题。
(1)建立层次结构模型,该模型共分为三个层次,三层次因素之间均为完全层次关系。
层次单排序及其一致性检验。
判断矩阵的构造因人而异,每个人给定的判断矩阵的兀素不一定相同。
对于总目标A ,准则层各因素构造判断矩阵A ,求解最大特征值;及其对应的特征向 量W (A),并进行一致性检验,即目标层,(2)构造判断矩阵、九急=4.1624, CR = 0.0609 < 0.1对于准则力i,准则层各因素构造判断矩阵B],求解最大特征值;1的?及其对应的特征向量W㈤),并进行一致性检验,即W lB1)=(0.0679 0.1524 0.3899 0.3899),蕴=4.0435, CR = 0.0161< 0.1对于准则万2,准则层各因素构造判断矩阵^2,求解最大特征值人捋;及其对应的特征向量/禺),并进行一致性检验,即W 阳=(0.5785 0.0718 0.2337 0.1161), 2^ = 4.2370,CR = 0.0878 < 0.1对于准则与,准则层各因素构造判断矩阵^3,求解最大特征值;I置及其对应的特征向量W(Bi),并进行一致性检验,即W,阳=(0.2554 0.1141 0.5806 0.0499),人捋;=4.0763, CR = 0.0283 < 0.1对于准则如,准则层各因素构造判断矩阵B.,求解最大特征值也及其对应的特征向量W㈤),并进行一致性检验,即W ㈤)=(0.5707 0.1318 0.0441 0.2534),九普;=4.1821, CR = 0.0674 <0.1以上各层次的判断矩阵均通过了一致性检验。
Review of Lecture 1n决策问题是Ø有不确定性的(概率)Ø复杂的偏好关系(效用)n决策分析的基石Ø效用Ø概率n决策要素包括ØA decision maker, frame , what you want, what youknow, what you can do,logic n决策树(结点与枝)Ø图形化表示决策问题Ø组织计算Ø决策分析与博弈分析范式区别n St. Petersburg Paradox Ø风险的价值测度使用期望效用Ø对数效用函数(考虑边际变化,边际效用递减)概率4.2Risk vs. uncertaintyn The risk versus uncertainty distinction is often used to distinguish between theories whichu do not make probability assignments (uncertainty) u use the (subjective or objective) assignment ofmathematical probabilities) (risk)Ø不确定性可以通过有限个未知参数来表示Ø参数的不确定性可以通过概率分布来表示概率计算n The probability of event A is p?1. I’m about to toss a coin. What is the probability of itcoming up Head?2. I consider parking my car on the street tonight. What isthe probability that it will be stolen overnight?3. I am about to undergo a medical operation. What is theprobability that I will survive it?4. What is the probability of war in the Middle East thisyear?两类学术观点n Frequentistu probability is the relative frequency of theoccurrence of an event in a large set of repetitions ofthe experiment (or in a large ensemble of identicalsystems) and is, as such, a property of a so-calledrandom variablen Bayesianu probability is not defined as a frequency ofoccurrence but as the plausibility that a propositionis true, given the available information. Probabilities are then—in the Bayesian view—not properties ofrandom variables but a quantitative encoding of ourstate of knowledge about these variables.Subjective Probability and Probability Spacen“Whether or not the difference (between subjective probability and objective probability) is importantphilosophically, we don’t feel it should make anydifference operationally…”n A triple (Ω,F,P) is called a probability space provided Ω is any set, F is a σ-algebra of subsets of Ω, and P is a probability measure on F.An example of ill-defined “randomness”n Bertrand’s paradox. Take a circle of radius 2 inches in the plane and choose a chord of this circle at random. What is the probability this chord intersects the concentric circle of radius 1 inch?主观概率与先验分布n现实决策中的结果的可能性几乎不可能通过大量重复实验来定义n根据决策人对事件的了解去设定,这样的概率反映了决策人对事件掌握的知识所建立起来的信念,称为主观概率u基于一定的公认假设,或者说公理系统,然后从这些假设出发,利用逻辑推理的方法导出。
实验十二多准则决策问题一实验目的通过用层次分析法解决一个多准则决策问题, 学习层次分析法的基本原理与方法; 掌握用层次分析法建立数学模型的基本步骤;学会用Mathematica解决层次分析法中的数学问题.二学习Mathematica命令有时在计算中只需求出实数解, 而省略复数解, 则可以输入调用只求实数解的软件包. 输入<<Miscellaneous\RealOnly.m即可.三实验的基本原理与方法层次分析法是一种简便、灵活而实用的多准则决策方法. 它特别适用于难以完全定量进行分析的,又相互关联、相互制约的众多因素构成的复杂问题. 它把人的思维过程层次化、数量化, 是系统分析的一个新型的数学方法.运用层次分析法建模,大体上可分四个基本步骤进行:1.建立层次结构首先对所面临的问题要掌握足够的信息. 搞清楚问题的范围、因素、各因素之间的相互关系,及所要解决问题的目标. 把问题条理化、层次化,构造出一个有层次的结构模型. 在这个模型下,复杂问题被分解为元素的组成部分. 这些元素又按其属性及关系形成若干层次.层次结构一般分三类:第一类为最高层,它是分析问题的预定目标和结果,也称目标层;第二类为中间层,它是为了实现目标所涉及的中间环节,如:准则、子准则,也称准则层;第三类为最低层,它包括了为实现目标可供选择的各种措施、决策方案等,也称方案层.图26.1层次结构应具有几个特点:(1) 从上到下顺序地存在支配关系,并用直线段表示. (2) 整个结构中层次数不受限制.2. 建立判断矩阵判断矩阵是层次分析的关键. 假定以上一层次的元素O 为准则,所支配的下一层次的元素为n C C C ,,,21 ,n 个元素n C C C ,,,21 对上一层次的元素O 有影响,要确定它们在O 中的比重.采用成对比较法.即每次取两个元素i C 和j C ,用ij a 表示i C 与j C 对O 的影响之比,全部比较的结果可用矩阵A 表示,().,,2,1,,n j i a A nn ij==⨯矩阵A 称为判断矩阵.定义1 若判断矩阵满足下列条件:().,,2,1,,1,1,0,n j i a a a a a A ii ijji ij nn ij===>=⨯ 则称判断矩阵A 为正互反矩阵.怎样确定判断矩阵A 的元素ij a 取值?当某层的元素n C C C ,,,21 对于上一层某元素O 的影响可直接定量表示时(如利润多少),i C 与j C 对O 的影响之比可以直接确定,ij a 的值也易得到.但对于大多数社会经济问题,特别是比较复杂的问题,元素i C 和j C 对O的重要性不容易直接获得,需要通过适当的方法解决.通常取数字1-9及其倒数作为ij a 的取值范围.这是因为在进行定性的成对比较时,人们头脑中通常有5个明显的等级:因素太多,将超出人们的判断比较能力,降低精确. 实践证明,成对比较的尺度以72±为宜. 故ij a 的取值范围是1,2,9, 及其倒数1,.91,,213. 计算层次单排序并做一致性检验层次单排序是指同一层次各个元素对于上一层次中的某个元素的相对重要性进行排序. 具体做法是:根据同一层n 个元素n C C C ,,,21 ,对上一层某元素O 的判断矩阵A 求出它们对于元素O 的相对排序权重,记为:n w w w ,,,21 .写成向量形式:()Tn w w w w ,,,21 = ,称为A 的排序权重向量. 其中i w 表示第i 个元素对上一层中某元素O 所占的比重. 从而得到层次单排序.层次单排序权重向量可有几种方法求解,常用的方法是利用判断矩阵A 的特征值与特征向量来计算排序权重向量w .为此引出矩阵的特征值与特征向量的有关理论.定义2 如果一个正互反矩阵().,,2,1,,n j i a A nn ij ==⨯满足),,2,1,,(n k j i a a a ik jk ij ==⨯,则称矩阵A 具有一致性,称元素k j i c c c ,,的成对比较是一致的; 并且称A 为一致矩阵.根据矩阵理论,可以得到如下几个定理.定理1 n 阶正互反矩阵A 的最大特征根m ax λn ≥,当n =λ时,A 是一致的. 定理2 n 阶正互反矩阵是一致矩阵的充分必要条件是最大特征值m ax λn =.计算排序权重向量方法和步骤:设()Tn w w w w ,,,21 =是n 阶判断矩阵的排序权重向量,当A 为一致矩阵时,根据n 阶判断矩阵构成的意义,显然有⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n n n nn n w w w w w w w w w w w w w w w w w w A 212221212111 (1) 因而满足 nw Aw =. 这里n 是矩阵A 的最大特征根,w 是相应的特征向量;当A 为一般的判断矩阵时w Aw max λ=. 其中m ax λ是A 的最大特征值(也称主特征根),w 是相应的特征向量(也称主特征向量). 经归一化后(即:∑==ni iw11),可近似作为排序权重向量,这种方法称为特征根法.一致性检验:在判断矩阵的构造中,并没有要求判断矩阵具有一致性的特点. 这是由于客观事物的复杂性与人的认识的多样性所决定.特别是在规模大、因素多的情况下,对于判断矩阵的每个元素来说,不可能求出精确的jiw w .但要求判断矩阵大体上应该是一致的. 一个经不起推敲的判断矩阵有可能导致决策的失误. 利用上述方法计算排序权向量,当判断矩阵过于偏离一致性时,其可靠程度也出现问题. 因此需要对判断矩阵的一致性进行检验. 其步骤如下:(1)计算一致性指标..I C1..max --=n nI C λ (2)当0..=I C 时,即n =max λ时,判断矩阵A 是一致的. 当..I C 值越大,判断矩阵A 的不一致的程度越严重.(2)查找相应的平均随机一致性指标..I R下表给出了n (从1—11)阶正互反矩阵,用了100—150个随机样本矩阵A 算出的随机一致性指标..I R......I R I C R C =(3) 当10.0..<R C 时,认为判断矩阵的一致性是可以接受的,否则应对判断矩阵作适当修正.4. 计算层次总排序权重并做一致性检验在得到了某层元素对其上一层中某元素的排序权重向量后,还需要得到各层元素,特别是最低层中各方案对于目标层的排序权重,即层次总排序权重向量,从而进行方案选择. 层次总排序权重要自上而下地将层次单排序的权重进行合成得到.考虑3个层次的决策问题. 若第一层只有1个元素,第二层有n 个元素,第三层有m 个元素,设第二层对第一层的层次单排序的权重向量为:()Tnw w w w )2()2(2)2(1)2(,,, =第三层对第二层的层次单排序的权重为:().,,2,1,,,,)3()3(2)3(1)3(n k w w w w Tkmk k k == 以)3(k w 为列向量构成矩阵()nm nm m m n n nw w w w w w w w w w w w W ⨯⎪⎪⎪⎪⎪⎭⎫ ⎝⎛==)3()3(2)3(1)3(2)3(22)3(12)3(1)3(21)3(11)3()3(2)3(1)3(,,, (4) 则第三层对第一层的层次总排序权重向量为)2()3()3(w W w = (5)一般地,若有s 层,则第k 层对第一层的总排序权重向量为s k w W w k k k ,,4,3,)1()()( ==- (6)其中)(k W 是以第k 层对第k-1层的排序权向量为列向量组成的矩阵,)1(-k w 是第k-1层对第一层的总排序权重向量. 按照上述递推公式,可得到最下层(第s 层)对第一层的总排序权重向量为)2()3()1()()(w W W W w s s s -= (7)层次总排序权重向量也要进行一致性检验. 具体方法是从最高层到最低层逐层进行. 定义3:若考虑的决策问题共有s 层. 设第l (s l ≤≤3)层的一致性指标为)1(.,,.,.)()(2)(1层元素的数目是第-l n I C I C I C l n l l ; 第l 层的随机一致性指标为 )()(2)(1.,,.,.l n l l I R I R I R ,令)1()(1)(1)(].,,.[.-=l l l l w I C I C I C (8) )1()(1)(1)(].,,.[.-=l l l l w I R I R I R (9)则第l 层对第一层的总排序权向量的一致性比率为s l I R I C RC RC l l l l ,,4,3,....)()()1()( =+=-. (10) 其中)2(.RC 为由(3)式计算的第二层对第一层的排序权向量的一致性比率.当最下层对第一层的总排序权向量的一致性比率1.0.)(<s R C 时,认为整个层次结构的比较判断可通过一致性检验.四 实验内容电脑的选购问题. 在选购电脑时,人们希望花最少的钱买到最理想的电脑. 下面通过层次分析法建立数学模型,以此确定欲选购的电脑. 模型建立的步骤可以分成四步:1. 建立购机的层次结构模型;2. 构造成对比较矩阵;3. 计算排序权重向量并做一致性检验;4. 计算层次总排序权重向量并做一致性检验. 下面按上述各步骤一一讨论研究. 1. 建立购机的层次结构模型图 26.2层次共有三层:最高层是“目标层”(用符号O 表示最终的选择目标);中间层是“准则层”(分别用符号1C ~5C 表示“性能”、“价格”、“质量”、“外观”、“售后服务”五个判断准则); 最低层是“方案层”(分别用符号1p ~3p 表示选定的三种品牌机:品牌1、品牌2、品牌3作为候选机型).选定了上述三种品牌机后,就要根据准则进行评定.2. 建立成对比较矩阵(1)建立“准则层”对“目标层”的成对比较矩阵根据表1的定量化尺度,根据建模者的个人观点,设“准则层”对“目标层”的成对比较矩阵为⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=1312313113121911312312122115139351A (11) (2)建立“方案层”对“准则层”的成对比较矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1251312151311B ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1215312151312B ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1251312151313B ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1213513121514B ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=111133131315B3. 计算排序权重向量并做一致性检验利用Mathematica 的Eigensystem 命令可得到矩阵A 的最大特征值及特征值所对应的特征向量. 输入:<<Miscellaneous\RealOnly.m (*调用只求实数运算的软件包*)A={{1.0, 5, 3, 9, 3}, {1/5, 1, 1/2, 2, 1/2}, {1/3, 2, 1, 3, 1},{1/9, 1/2, 1/3, 1, 1/3}, {1/3, 2, 1, 3, 1}};(*以小数形式1.0输入, 进行近似计算,可避免精确解太长、太复杂*) T=Eigensystem[A]//Chop (*输入//Chop,把与零非常接近的数换成零*)输出为:{{5.00974, Nonreal, Nonreal, 0, 0},{{0.88126, 0.167913, 0.304926, 0.0960557, 0.304926}, {0.742882, Nonreal, Nonreal, Nonreal, Nonreal}, {0.742882, Nonreal, Nonreal, Nonreal, Nonreal},{-0.993398, 0, 0.0673976, 0.0662265, 0.0650555}, {-0.65676, 0, 0.57431, 0.043784, -0.486742}}}(输出中的Nonreal 表示复数)得到A 的最大特征值00974.5max =λ,以及00974.5max =λ所对应的特征向量()T x 304926.0,0960557.0,304926.0,167913.0,88126.0=输入Clear[x];x=T[[2,1]];ww2=x/Apply[Plus, x]得归一化后的特征向量:()T w 173739.0,0547301.0,173739.0,0956728.0,502119.0)2(=计算一致性指标1..max --=n nI C λ其中5=n ,00974.5max =λ, 得..I C =0.002435.查表得到相应的随机一致性指标12.1..=I R得到一致性比例......)2(I R I C R C ==0.002174 故1.0..)2(<R C ,通过了一致性检验. 此时可以认为A 的一致性程度在容许的范围之内,可以用其归一化后的特征向量()T w 173739.0,0547301.0,173739.0,0956728.0,502119.0)2(=作为其排序权向量.再求矩阵)5,,2,1( =j B j 的最大特征值及特征值所对应的特征向量. 输入命令B1=B3={{1.0, 1/3, 1/5}, {3, 1, 1/2}, {5, 2, 1}};B2=Transpose[B1];B4={{1.0, 5, 3}, {1/5, 1, 1/2}, {1/3, 2, 1}}; B5={{1.0, 3, 3}, {1/3, 1, 1}, {1/3, 1, 1}};T1=Eigensystem[B1]//Chop T2=Eigensystem[B2]//Chop T3=Eigensystem[B3]//Chop T4=Eigensystem[B4]//Chop T5=Eigensystem[B5]//Chop输出分别为{{3.00369,Nonreal,Nonreal}, {{0.163954,0.46286,0.871137}, {Nonreal,Nonreal,0.871137}, {Nonreal,Nonreal,0.871137}}};{{3.00369,Nonreal,Nonreal}, {{0.928119,0.328758,0.174679}, {0.928119,Nonreal,Nonreal}, {0.928119,Nonreal,Nonreal}}}{{3.00369,Nonreal,Nonreal}, {{0.163954,0.46286,0.871137}, {Nonreal,Nonreal,0.871137}, {Nonreal,Nonreal,0.871137}}}{{3.00369,Nonreal,Nonreal}, {{0.928119,0.174679,0.328758}, {0.928119,Nonreal,Nonreal}, {0.928119,Nonreal,Nonreal}}}{{3.,0,0},{{0.904534,0.301511,0.301511}, {-0.973329,0.162221,0.162221}, {-0.170182,-0.667851,0.724578}}}从输出可以分别得到)5,,2,1( =j B j 的最大特征值为000.3,00369.3,00369.3,00369.3,00369.354321=====λλλλλ,以及上述特征值所对应的特征向量为()()()()()T TTTT x x x x x 301511.0,301511.0,904534.0328758.0,174679.0,928119.0871137.0,46286.0,163954.0174679.0,328758.0,928119.0871137.0,46286.0,163954.054321=====其中.5,,2,1),,,(321 ==i x x x x i i i i 为了求得归一化后(即:.5,,2,1,131==∑=i xj ij)的特征向量:输入Clear[x1,x2,x3,x4,x5];x1=T1[[2,1]]; w1=x1/Apply[Plus, x1]x2=T2[[2,1]]; w2=x2/Apply[Plus, x2]x3=T3[[2,1]]; w3=x3/Apply[Plus, x3]x4=T4[[2,1]]; w4=x4/Apply[Plus, x4]x5=T5[[2,1]]; w5=x5/Apply[Plus, x5]得()()()()()TT T TTw w w w w 200000.0,200000.0,600000.0229651.0,12202.0,648329.0581552.0,308996.0,109452.012202.0,229651.0,648329.0581552.0,308996.0,109452.054321=====为计算一致性指标,.5,,2,1,1. =--=i n nI C i i λ其中3=n ,输入lamda={T1[[1,1]], T2[[1,1]], T3[[1,1]], T4[[1,1]], T5[[1,1]]}CI=(lamda-3)/(3-1)//Chop得0.,0018473.0.,0018473.0.,0018473.0.,0018473.0.54321=====I C I C I C I C I C查表得到相应的随机一致性指标)5,,2,1(58.0. ==i I R i计算一致性比例.5,,2,1,... ==i I R I C R C iii 输入CR=CI/0.58得0.;003185.0.;003185.0.;003185.0.;003185.0.54321=====R C R C R C R C R C .故)5,,2,1(,1.0. =<i R C i ,通过了一致性检验. 此时可以认为)5,,2,1( =j B j 的一致性程度在容许的范围之内,可以用其特征向量(归一化后)作为其排序权向量.4. 计算层次总排序权重向量并做一致性检验 列表表示各数据如下:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=2.0229651.0581552.012202.0581552.02.012202.0308996.0229651.0308996.06.0648329.0109452.0648329.0109452.0)3(W)3(W 即是第三层对第二层的权重向量为列向量组成的矩阵. 最下层(第三层)对最上层(第一层)的总排序权向量为)2()3()3(w W w =为了计算上式, 输入W3=Transpose[{w1, w2, w3, w4, w5}];ww3=W3.ww2得到输出()T w 452037.0,272235.0,275728.0)3(=为了对总排序权向量进行一致性检验, 计算())2(521)3(.,,.,..w I C I C I C I C =输入CI.ww2得0.00152635.)3(=I C再计算)2(51)3(].,.[.w I R I R I R =输入RI=Table[0.58,{j,5}];RI.ww2得58.0.)3(=I R再计算)3()3()2()3(....I R I C RC RC +=得0.00480575.)3(=R C因为1.0.)3(<R C ,所以总排序权重向量符合一致性要求的范围. 根据总排序权重向量的分量取值,品牌3的电脑是建模者对这三种品牌机的首选.五 实验作业1. 根据你的设想购置一台计算机,需考虑什么样的判断准则?利用上述层次分析法及数学软件做出最佳的决策.2. 根据你的经历设想如何报考大学,需要什么样的判断准则?利用上述层次分析法及数学软件做出最佳的决策.(注:可编辑下载,若有不当之处,请指正,谢谢!)。