大学物理23.2单缝夫琅禾费衍射和光栅衍射.

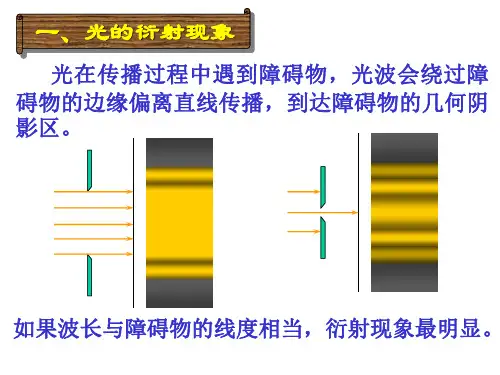
第四章 光的衍射一、基本知识点光的衍射：当光遇到小孔、狭缝或其他的很小障碍物时，传播方向将发生偏转，而绕过障碍物继续前行，并在光屏上形成明暗相间的圆环或条纹。

光波的这种现象称为光的衍射。

菲涅耳衍射：光源、观察屏（或者是两者之一）到衍射屏的距离是有限的，这类衍射又称为近场衍射。

夫琅禾费衍射：光源、观察屏到衍射屏的距离均为无限远，这类衍射也称为远场衍射。

惠更斯－菲涅耳原理：光波在空间传播到的各点，都可以看作一个子波源，发出新的子波，在传播到空间某一点时，各个子波之间可以相互叠加。

这称为惠更斯－菲涅耳原理。

菲涅耳半波带法：将宽度为a 的缝AB 沿着与狭缝平行方向分成一系列宽度相等的窄条，1AA ，12A A ，…，k A B ，对于衍射角为θ的各条光线，相邻窄条对应点发出的光线到达观察屏的光程差为半个波长，这样等宽的窄条称为半波带。

这种分析方法称为菲涅耳半波带法。

单缝夫琅禾费衍射明纹条件：sin (21)(1,2,...)2a k k λθ=±+=单缝夫琅禾费衍射暗纹条件：sin (1,2,...)a k k θλ=±=在近轴条件下，θ很小，sin θθ≈, 则第一级暗纹的衍射角为 1aλθ±=±第一级暗纹离开中心轴的距离为 11x f faλθ±±==±, 式中f 为透镜的焦距。

中央明纹的角宽度为 112aλθθθ-∆=-=中央明纹的线宽度为 002tan 2l f f faλθθ=≈∆=衍射图样的特征：① 中央明纹的宽度是各级明纹的宽度的两倍，且绝大部分光能都落在中央明纹上。

② 暗条纹是等间隔的。

③ 当入射光为白光时，除中央明区为白色条纹外，两侧为由紫到红排列的彩色的衍射光谱。

④ 当波长一定时，狭缝的宽度愈小，衍射愈显著。

光栅: 具有周期性空间结构或光学性能（透射率，反射率和折射率等）的衍射屏，统称为光栅。

光栅常数: 每两条狭缝间距离d a b =+称为光栅常数。

物理实验居家单缝夫琅禾费衍射实验数据及完整实验报告和结论2020年春季大学物理实验单缝夫琅禾费衍射专业班级：学号：姓名：日期：实验名称：单缝夫琅禾费衍射实验目的：观察激光通过单缝后的夫琅禾费衍射现象，测量出单缝宽度参考时，麻烦注意数据和格式的替换，楼主也是学生党，这是我自己的实验报告实验仪器材料：激光笔、书本、墙壁、皮尺、胶水、直尺实验方案设计：1.设单缝宽度AB=a，单缝到接收屏之间的距离是L，衍射角为Ф的光线聚到屏上P 点，P点到中央明纹中心距离X K，那么A、B出射光线到P点的光程差则为asinФ2.当光程差是半波长的偶数倍时形成暗纹，由于Ф很小，asinФ≈aX K /L，即当aX K /L=kλ时，出现暗纹，由此得到单缝宽度：a=LKλ/ X K实验过程：参考时，麻烦注意数据和格式的替换，楼主也是学生党，这是我自己的实验报告1. 用两张银行卡自制狭缝，并用书本固定，激光笔发出红光，照射狭缝，调整远处墙壁可初步观察到明显的夫琅禾费衍射现象2. 测量狭缝和墙壁的距离L，测量暗环中心到中央明纹中心的距离X K，可选择第1级（K=±1）或第2级（K=±2）暗纹，共测量5次，取平均值3. 通过上述公式计算出狭缝宽度，激光波长参考：红光650nm问题：手持激光笔摇晃严重，增加测量难度；办法：用胶水固定激光笔数据分析处理：参考时，麻烦注意数据和格式的替换，楼主也是学生党，这是我自己的实验报告将上述实验数据代入公式a=LKλ/ X K，可以得到K=1时，计算得到狭缝的宽度为0.455mm；K=2时，计算得到狭缝的宽度为0.456mm K=3时，计算得到狭缝的宽度为0.455mm综上，测量得到狭缝的宽度为0.455mm实验小结：激光笔红光波长与参考值存在误差；狭缝和墙壁的距离L因皮尺精度有限，读数不准虽然大学物理的课程未涉及本次实验知识，但通过这次实验也让我对光学相关知识有了更深层次的了解，提高了兴趣-全文完-。

§ 14.3光的夫琅和费衍射一. 单缝夫琅和费衍射 二. 圆孔夫琅和费衍射 ▲三. 光栅夫琅和费衍射 单缝衍射：a ↓: ∆ϕ ↑; I ↓平行、等宽、等间距的多狭缝(或反射面) 构成的光学元件解决办法： 采用一系列平行单缝 光栅：从工作原理分: 衍射光栅(透射光栅) 反射光栅(闪耀光栅)透射光栅:刻痕玻璃在玻璃片上刻划出一系列平行等距的划痕,刻过 的地方不透光，未刻地方透光。

N条未刻： 透光缝 刻：遮光l光栅常数:l d =a+b= N(10 ~ 10 cm)−3−4装置：思路: （1）先不计缝宽，将每缝光强各集中于一个线光源： 讨论N个几何线光源的干涉 （2） 计及缝宽：加上N个单缝衍射的影响1. N 缝(几何线光源)干涉 （1）光强分布用多边形法则进行 N 个大小相等， （P395 例一） 两两依次相差为 δ 的光振动的叠加λ∆d∆ = d sin ϕϕ∆ ∆FPfδ =2π d sin ϕλπ d sin ϕ β = = λ 2δωRMCδNδr Ar A2rδ ANA 1 = 2 R sinδδ2δ δNδ A = 2 R sin 2 NδsinOϕr A1δxP2 = A ⋅ sin Nβ A = A1 ⋅ 1 δ sin β sin 2光强分布：sinNβ 2 ) I = I1( sinβ一般情况明纹中心（主明纹、主极大）sinNβ 2 ) I = I1( sinβωRMrδ ANI = N I12CδNδr Ar A2暗纹中心δ δI =0xδr r A1 r AN A = 0r A2Oϕδr A1δP（2）条纹特点（半定量讨论） 1）明纹中心（主明纹、主极大）条件 光栅公式：kλbadϕϕ∆ = d sin ϕ = ( a + b ) sin ϕ = kλ(k = 0，1， 2L ± ± )f光栅公式： ∆ = d sin ϕ = ( a + b ) sin ϕ = k λ(k = 0，1， 2L ± ± )主明纹角位置：sin ϕ = k亮度：λdI = N 2 I1最高级次：Q| sin ϕ |< 1λ∴ km <λdd d (例： = 4 ⋅ 2, k m = 4; = 4, k m = 3)λ例：分光计作光栅实验，用波长 λ = 632.8 nm的激光 照射光栅常数 d = 1/300 mm的光栅上，问最多能看到 几条谱线。

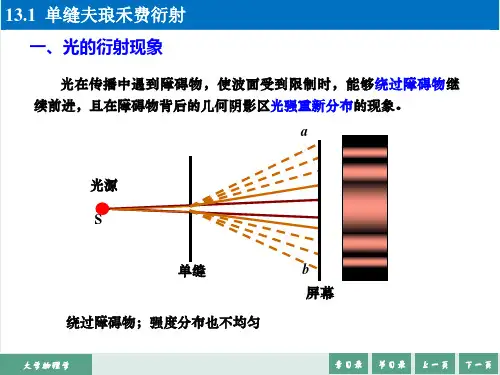
光栅衍射和单缝衍射的关系
光栅衍射和单缝衍射是两种不同的光学现象，但它们之间存在一定的关系。

单缝衍射是当光通过一个狭窄的缝隙时，由于光波的干涉和衍射作用，会在屏幕上出现明暗相间的条纹。

这些条纹是单缝里波阵面上各点所有子波互相干涉的结果。

光栅衍射则是当光通过一个刻有密集平行狭缝的光栅时，会形成明暗相间的干涉条纹。

这些条纹是光栅上每个缝发出的各波的干涉以及各缝的衍射光互相干涉的结果。

换句话说，光栅具有单缝衍射和多光束干涉的总和作用。

在光栅衍射中，单缝衍射起着勾画光栅图样轮廓的作用，而多光束干涉则起着填补轮廓内多光束干涉的各级主极大的作用。

由于每个缝上出来的光再在各缝间干涉加强，所以明纹特别亮。

同时，因为形成暗纹的机会比明纹的多，所以暗区特别宽，用光栅衍射测定波长较为准确。

总的来说，光栅衍射是单缝衍射和多缝干涉的综合结果，因此光栅衍射同时保留着单缝衍射的痕迹。

以上信息仅供参考，如果想要了解更多专业解释，可以查阅光学书籍或咨询物理学家。