下载文档原格式
测定单缝衍射的光强分布【教学目的】１．观察单缝衍射现象，加深对衍射理论的理解。
２．会用光电元件测量单缝衍射的相对光强分布，掌握其分布规律。
３．学会用衍射法测量微小量。
【教学重点】1.夫琅禾费衍射理论2.夫琅禾费单缝衍射装置3.用光电元件测量单缝衍射的相对光强分布，衍射法测量微小量【教学难点】夫琅禾费单缝衍射光路及光强分布规律【课程讲授】提问：1. 缝宽的变化对衍射条纹有什么影响？2. 夫琅和费衍射应符合什么条件？一、实验原理光的衍射现象是光的波动性的重要表现。
根据光源及观察衍射图象的屏幕（衍射屏）到产生衍射的障碍物的距离不同，分为菲涅耳衍射和夫琅禾费衍射两种，前者是光源和衍射屏到衍射物的距离为有限远时的衍射，即所谓近场衍射；后者则为无限远时的衍射，即所谓远场衍射。
要实现夫琅禾费衍射，必须保证光源至单缝的距离和单缝到衍射屏的距离均为无限远（或相当于无限远），即要求照射到单缝上的入射光、衍射光都为平行光，屏应放到相当远处，在实验中只用两个透镜即可达到此要求。
实验光路如图1所示，图1 夫琅禾费单缝衍射光路图与狭缝E 垂直的衍射光束会聚于屏上P 0处，是中央明纹的中心，光强最大，设为I 0，与光轴方向成Ф角的衍射光束会聚于屏上P A 处，P A 的光强由计算可得：式中，b 为狭缝的宽度，λ为单色光的波长，当0=β时，光强最大，称为主极大，主极大的强度决定于光强的强度和缝的宽度。
当πβk =，即：时，出现暗条纹。
除了主极大之外，两相邻暗纹之间都有一个次极大，由数学计算可得出现这些次极大的位置在β=±1.43π，±2.46π，±3.47π，…，这些次极大的相对光强I/I 0依次为0.047，0.017，0.008，…图2 夫琅禾费衍射的光强分布夫琅禾费衍射的光强分布如图2所示。
220sin ββI I A =)sin (λφπβb =b Kλφ=sin ），，，⋅⋅⋅±±±=321(K图3 夫琅禾费单缝衍射的简化装置用氦氖激光器作光源，则由于激光束的方向性好，能量集中，且缝的宽度b 一般很小，这样就可以不用透镜L 1，若观察屏（接受器）距离狭缝也较远（即D 远大于b ）则透镜L 2也可以不用，这样夫琅禾费单缝衍射装置就简化为图3，这时，由上二式可得二、实验装置激光器座、半导体激光器、导轨、二维调节架、一维光强测试装置、分划板 、可调狭缝、平行光管、起偏检偏装置、光电探头 、小孔屏、 数字式检流计、专用测量线等。
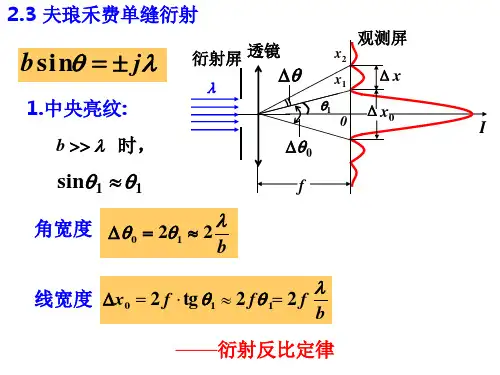
利用夫琅与费单缝衍射对角宽度的测量观察衍射现象的实验装置一般就是由光源、衍射屏与接受屏三部分组成。
按它们相互间距离的不同情况,通常将衍射分为两类:一类就是衍射屏离光源或接受屏的距离为有限远时的衍射,称为菲涅尔衍射;另一类就是衍射屏与光源与接受屏的距离都就是无穷远的衍射,也就就是照射到衍射屏上的入射光与离开衍射屏的衍射光都就是平行光的衍射,称为夫琅禾费衍射。
若衍射屏上有一单狭缝,宽度为a,则在接受屏上将出现一组明暗相间的平行直条纹。
一、实验目的1、观察单缝衍射现象,了解单缝宽度对衍射条纹的影响。
2、学习测量单缝宽度的一种方法。
二、实验原理让一束单色平行光通过宽度可调的缝隙,射到其后的接收屏上。
,若缝隙的宽度a 足够大,接收屏上将出现亮度均匀的光斑。
随着缝隙宽度a 变小,光斑的宽度也相应变小。
但当缝隙宽度小到一定程度时, 光斑的区域将变大,并且原来亮度均匀的光斑变成了一系列亮暗相间的条纹。
根据惠更斯-菲涅耳原理,接收屏上的这些亮暗条纹,就是由于从同一个波前上发出的子波产生干涉的结果。
为满足夫琅禾费衍射的条件,必须将衍射屏放置在两个透镜之间。
实验光路图如图17-1所示。
r r 0OX'x k f θL 1L 2S 2S 1图17-1夫琅禾费单缝衍射光路图下面来推导单缝缝宽的测量公式 。
中央亮条纹的宽度可用其两侧暗条纹之间的角距离来表示,由于对称性, 主极大的角宽度为从点O 到第一暗条纹中心的角距离的两倍,所以从点O 到第一暗条纹中心的角距离,称为主极大的半角宽度。
主极大的半角宽度就就是第一暗条纹的衍射角θ,近似等于a /λ。
中央亮条纹的宽度等于各次极大的两倍,也就就是说,各次极大的角宽度都等于中央亮条纹的半角宽度,并且绝大部分光能都落在了中央亮条纹上。
在远场条件下,即单缝至屏距离a z >>时,各级暗条纹衍射角k θ很小,k k θθ≈sin ,于就是第k 级暗条纹在接收屏上距中心的距离k x 可写为f x k k θ=。
