单缝和圆孔夫琅禾费衍射介绍
- 格式：ppt
- 大小：904.00 KB
- 文档页数：15
文档推荐
-
2.3 夫琅禾费单缝衍射页数:26
-
测定夫琅禾费衍射实验页数:6
-
夫琅禾费单缝衍射光强分布的研究页数:6
-
单缝夫琅和费衍射的光强分布页数:6
-
单缝夫琅禾费衍射强度页数:2
-
夫琅禾费单缝衍射页数:2
-
夫琅和费单缝衍射的光强问题页数:8
下载文档原格式
合集下载
圆孔的夫朗和费衍射
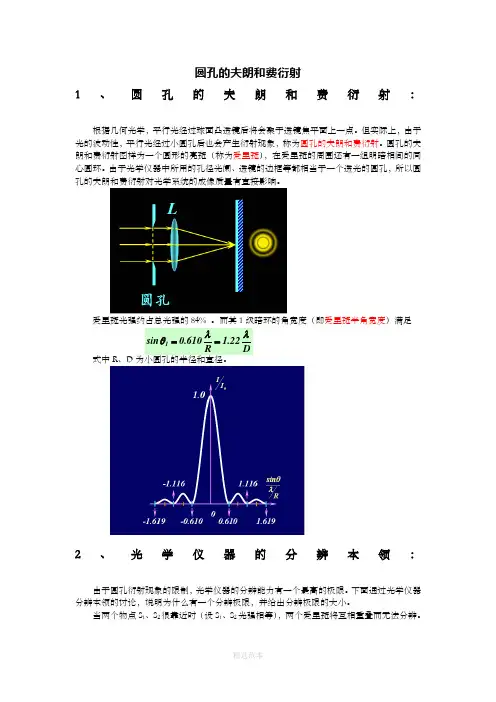
圆孔的夫朗和费衍射1、圆孔的夫朗和费衍射：根据几何光学，平行光经过球面凸透镜后将会聚于透镜焦平面上一点。
但实际上，由于光的波动性，平行光经过小圆孔后也会产生衍射现象，称为圆孔的夫朗和费衍射。
圆孔的夫朗和费衍射图样为一个圆形的亮斑（称为爱里斑），在爱里斑的周围还有一组明暗相间的同心圆环。
由于光学仪器中所用的孔径光阑、透镜的边框等都相当于一个透光的圆孔，所以圆孔的夫朗和费衍射对光学系统的成像质量有直接影响。
爱里斑光强约占总光强的84% 。
而其1级暗环的角宽度（即爱里斑半角宽度）满足D 22.1R610.0sin 1λλθ==式中R 、D 为小圆孔的半径和直径。
2、光学仪器的分辨本领：由于圆孔衍射现象的限制，光学仪器的分辨能力有一个最高的极限。
下面通过光学仪器分辨本领的讨论，说明为什么有一个分辨极限，并给出分辨极限的大小。
当两个物点S 1、S 2很靠近时（设S 1、S 2光强相等），两个爱里斑将互相重叠而无法分辨。
对一个光学仪器来说，若一个点光源产生的爱里斑的中央刚好与另一个点光源产生的爱里斑瑞的1级暗环相重合，这时两个爱里斑重合部分的光强约为单个爱里斑中央光强的80%左右，一般人眼刚好能分辨出这是两个光点的像。
因此，满足上述条件的两个点光源恰好能被该光学仪器所分辨。
这一条件称为瑞利分辨判据。
（见下图）恰能分辨时两光源发出的光线对透镜光心的夹角Δθ 称为最小分辨角，用δθ表示。
由上讨论可知，最小分辨角δθ等于爱里斑的半角宽度θ1：)D 22.1arcsin(1λθδθ==尤其当θ1 ~ 0D 22.1λδθ≈（或称分辨率），用R 表示：λδθ22.1D 1R ==讨论：⑴ 增大透镜的直径D 可提高镜头的分辨率。
光学天文望远镜的镜头孔径可达数米！ ⑵ 设r 、d 为爱里斑的半径和直径，则：f 2d f r D 22.1===λδθ即：D f44.2d λ=f D称为镜头的相对孔径（越大越好）。
如照相机镜头上所标示的502:1字样，即表示镜头的焦距mm 50f =，而镜头的孔径mm 25D =。
单缝和圆孔的夫琅禾费衍射介绍
2
明纹在屏上的位置
x f sin f (2k 1)
2a
k ax 1 3.5 0.5 3
f 2
第3级明 纹
（2）对应于 p点缝可分成多少个半波带？
asin (2k 1)
2
(23 1) 7
22
7个半波带
（3）将缝宽增加1倍，p 点将变为什么条纹？
y2 = u
-2 - o
··
··
2 u
-2.46π -1.43π
+1.43π +2.46π
u 1.43， 2.46， 3.47，…
相应 asin 1.43, 2.46, 3.47,…
三、入射光非垂直入射时光程差的计算
DB BC
b(sin sin)
“半波带”发的光在 P处干涉相消形成暗纹。
当asin=3/2时，可将缝分为3个半波带.
a
AA
A1
p
B
A2 C
o
B /2
相邻半波带的相对应点光程差均是/2,两个
“半波带”发的光在 P处干涉相消形成暗纹。第 3个“半波带”发的光在 P形成明纹。
一般情况下，可将缝分为k个半波带，当k为偶数 时，p点为暗纹，当k为奇数时，p点为明纹。
例3 在单缝衍射中，若使单缝和透镜分别 稍向上移，则衍射条纹将如何变化？ 解：
o
⑴单缝上移衍射光束向上平移经透镜聚焦后， 位置不变条纹不变 ⑵透镜上移衍射光束经透镜聚焦后，位置随之 上移条纹向上平移
例4 在单缝夫琅和费衍射实验中，缝宽a=10，缝 后透镜焦距 f =40cm , 试求第一级明纹的角宽度，线 宽度以及中央明纹的线宽度。
明纹在屏上的位置
x f sin f (2k 1)
2a
k ax 1 3.5 0.5 3
f 2
第3级明 纹
（2）对应于 p点缝可分成多少个半波带？
asin (2k 1)
2
(23 1) 7
22
7个半波带
（3）将缝宽增加1倍，p 点将变为什么条纹？
y2 = u
-2 - o
··
··
2 u
-2.46π -1.43π
+1.43π +2.46π
u 1.43， 2.46， 3.47，…
相应 asin 1.43, 2.46, 3.47,…
三、入射光非垂直入射时光程差的计算
DB BC
b(sin sin)
“半波带”发的光在 P处干涉相消形成暗纹。
当asin=3/2时，可将缝分为3个半波带.
a
AA
A1
p
B
A2 C
o
B /2
相邻半波带的相对应点光程差均是/2,两个
“半波带”发的光在 P处干涉相消形成暗纹。第 3个“半波带”发的光在 P形成明纹。
一般情况下，可将缝分为k个半波带，当k为偶数 时，p点为暗纹，当k为奇数时，p点为明纹。
例3 在单缝衍射中，若使单缝和透镜分别 稍向上移，则衍射条纹将如何变化？ 解：
o
⑴单缝上移衍射光束向上平移经透镜聚焦后， 位置不变条纹不变 ⑵透镜上移衍射光束经透镜聚焦后，位置随之 上移条纹向上平移
例4 在单缝夫琅和费衍射实验中，缝宽a=10，缝 后透镜焦距 f =40cm , 试求第一级明纹的角宽度，线 宽度以及中央明纹的线宽度。
2—3 夫琅和费单缝衍射
3、狭缝上所有次波在P 的叠加
积分过程见（附录2－1） b sinu u sin A A A0 sincu 令 p 0 u
2 sin u 2 2 2 2 Ap A0 A sin c u 0 2 u
I p I 0 sinc 2 u P点光强随θ的分布
16
三、强度公式的讨论 1、最大最小位置：
y2 = u
-
·
-2.46
·
-1.43
· 0
0
+1.43
+2.46
解得 :
相应 :
u 1.43， 2.46， 3.47， „
b sin 1.43 , 2.46 , 3.47 ,„
19
前几个次最大的位置
次最大序号 次最大位置 相对强度
u
1.43 2.46
(k 1, 2, ) 暗纹 (k 1, 2, ) 明纹 中央明纹
•正、负号表示衍射条纹对称分布于中央明纹的两侧 •对于任意衍射角，单缝不能分成整数个半波带，
在屏幕上光强介于最明与最暗之间。
方法一、菲涅耳半波带法
I / I0
明纹宽度
中央明条纹的角宽度 为中央两侧第一暗条纹 之间的区域:
3.47
4.48
sin
3 2b 5 2.46 b 2b 7 3.47 b 2b 9 4.48 b 2b 1.43 b
I I 0
1 2 3 4
0.047
0.017
0.008
0.005
1 sin k0 k 2 b
b
0
sin (2k 1)
2b
物理大学物理惠更斯单缝圆孔衍射
演示：单缝、圆孔、单丝
一．光的衍射现象
光在传播过程中能绕过障碍物 的边缘而偏离直线传播的现象 特征： 光不仅能绕过障碍物传播， 而且还能产生明暗相间的条纹 根据惠更斯原理能很自然地解释波在障碍物附近 发生的衍射现象，
但却不能说明光在衍射的同时， 为什么会出现明暗相间的条纹。
惠更斯原理
• 在波的传播过程中，波阵面（波前）上的 每一点都可看作是发射子波的波源 (点波源)。
E
B
aC
A
2
●P
a
●
●
●
●
●
●
●
●
●
半波带 半波带 半波带
另外，单缝波阵面AB 被这些平行平面分成许多等宽的条带， 相邻条带上对应点发出的光在P点的光程差为λ/2 （半个波长）
相邻两波带发出的子波相位差为
相邻两条带发出的光在P点相干叠加时将相互抵消 这样的条带称为半波带， 利用这样的半波带分析衍射图样的方法叫半波带法。
S
●
根据惠——菲原理，单缝后面空间任一点的光振动 是单缝波阵面上窄条子波源发出柱面光波 传到该点的相干叠加
3. 定性解释
E
L2
L1
a
a●
S
子波源沿某一方向的波线——衍射线 衍射线与单缝面法线的夹角——衍射角
显然单缝面上各个子波源沿同一衍射角发射的子波 构成一平行光束
3. 定性解释 L2
L1
●
a●
光衍射分类 根据障碍物与光源和观察屏之间的距离来分
1) 近场衍射（菲涅耳衍射）
障碍物与光源或观察屏的
距离是有限远时。
S
观察比较方便， 但定量计算却很复杂。
RP
2) 远场衍射（夫琅禾费衍射） 障碍物与光源和观察屏的 距离是无限远时。 计算比较简单。 物理含义?
一．光的衍射现象
光在传播过程中能绕过障碍物 的边缘而偏离直线传播的现象 特征： 光不仅能绕过障碍物传播， 而且还能产生明暗相间的条纹 根据惠更斯原理能很自然地解释波在障碍物附近 发生的衍射现象，
但却不能说明光在衍射的同时， 为什么会出现明暗相间的条纹。
惠更斯原理
• 在波的传播过程中，波阵面（波前）上的 每一点都可看作是发射子波的波源 (点波源)。
E
B
aC
A
2
●P
a
●
●
●
●
●
●
●
●
●
半波带 半波带 半波带
另外，单缝波阵面AB 被这些平行平面分成许多等宽的条带， 相邻条带上对应点发出的光在P点的光程差为λ/2 （半个波长）
相邻两波带发出的子波相位差为
相邻两条带发出的光在P点相干叠加时将相互抵消 这样的条带称为半波带， 利用这样的半波带分析衍射图样的方法叫半波带法。
S
●
根据惠——菲原理，单缝后面空间任一点的光振动 是单缝波阵面上窄条子波源发出柱面光波 传到该点的相干叠加
3. 定性解释
E
L2
L1
a
a●
S
子波源沿某一方向的波线——衍射线 衍射线与单缝面法线的夹角——衍射角
显然单缝面上各个子波源沿同一衍射角发射的子波 构成一平行光束
3. 定性解释 L2
L1
●
a●
光衍射分类 根据障碍物与光源和观察屏之间的距离来分
1) 近场衍射（菲涅耳衍射）
障碍物与光源或观察屏的
距离是有限远时。
S
观察比较方便， 但定量计算却很复杂。
RP
2) 远场衍射（夫琅禾费衍射） 障碍物与光源和观察屏的 距离是无限远时。 计算比较简单。 物理含义?
4-5 单缝和圆孔的夫琅禾费衍射
3) 任意相邻的半波带上的对应点的子波光程差为 ， 2 π
，所以达到P点时将完全相互抵消。
4
R
A1
A
L
P
Q
BC a sin
B
A2
C
o
/2
讨论： 1) 半波带数为整数，且为偶数时
a sin 2k
2
k
干涉相消（暗纹）
2) 半波带数为整数，且为奇数时
a sin ( 2k 1)
15
I I0
1.43 2.46 a a
3
1.43
a
2
2.46
a
a
3
a
2
a
a
o
a
a
sin
16
二、圆孔的夫琅禾费衍射
中央是个明亮的圆斑，外围是一组同心的明环 17 和暗环。中央明区集中了光能的83.8%。
L2 D f
p
0 0
d
第一暗环对应的衍射角0称为艾里斑的半角 宽 (它标志着衍射的程度) ，理论计算得：
2
k
x kf a
sin k a
x k a sin a f
6
第一暗纹距中心的距离: 线度： x1 f
a
角度：
sin 1
a
a a （2）中央明纹：主极大(k = 1两暗纹之间)
第一暗纹的衍射角
1 arcsin
0 ，相当于到达屏上O点的各衍射子波的相位 相同，产生了最大的光强，是零级衍射斑的中心。
单缝、圆孔衍射
这就是光的衍射现象。
缝
屏
缝
屏
光通过宽狭缝
光通过窄狭缝
衍射屏
观察屏
*
S
a
单缝
小孔衍射
矩形孔缝
二、衍射的分类 根据光源缝、和屏的位置的不同分：
光源无限远 射向无限远 菲涅耳衍射 夫琅和费衍射
在实验中的夫琅禾费衍射
缝平面 透镜L
观察屏
透镜L
*
f
S
B Aδ
p · 0 f
a
S: 单色线光源
2
a
a sin
两相邻半波带上对应点发的 光在P 处干涉相消。
P
3 •当 a sin 时,可将缝分成三个“半波带” 2
B θ
P 处为明纹中心
a
A λ /2
•当 a sin 2 时,可将缝分成四个“半波带”
B θ a A λ /2
P 处干涉相消形成暗纹
由半波带法可得明暗纹条件为：
a sin
0, 0
*
f
S
B
a
0
A
O点—— 中央明纹(中心)
f
菲涅耳半波带法 在波阵面上截取一个条状带，使它上下两边缘发 的光在屏上 p 处的光程差为 ，此带称为半波带。
2
θ
1 2 1′ 2′ 1 2 1′ 2′
a
B 半波带
半波带 半波带
半波带
A
λ /2
菲涅耳半波带法
例题1 水银灯发出的波长为546nm的绿色平行光，垂直入射于 宽0.437mm的单缝，缝后放置一焦距为40cm的透镜，试求在透镜 焦面上出现的衍射条纹中央明纹的宽度。
缝
屏
缝
屏
光通过宽狭缝
光通过窄狭缝
衍射屏
观察屏
*
S
a
单缝
小孔衍射
矩形孔缝
二、衍射的分类 根据光源缝、和屏的位置的不同分：
光源无限远 射向无限远 菲涅耳衍射 夫琅和费衍射
在实验中的夫琅禾费衍射
缝平面 透镜L
观察屏
透镜L
*
f
S
B Aδ
p · 0 f
a
S: 单色线光源
2
a
a sin
两相邻半波带上对应点发的 光在P 处干涉相消。
P
3 •当 a sin 时,可将缝分成三个“半波带” 2
B θ
P 处为明纹中心
a
A λ /2
•当 a sin 2 时,可将缝分成四个“半波带”
B θ a A λ /2
P 处干涉相消形成暗纹
由半波带法可得明暗纹条件为：
a sin
0, 0
*
f
S
B
a
0
A
O点—— 中央明纹(中心)
f
菲涅耳半波带法 在波阵面上截取一个条状带，使它上下两边缘发 的光在屏上 p 处的光程差为 ，此带称为半波带。
2
θ
1 2 1′ 2′ 1 2 1′ 2′
a
B 半波带
半波带 半波带
半波带
A
λ /2
菲涅耳半波带法
例题1 水银灯发出的波长为546nm的绿色平行光，垂直入射于 宽0.437mm的单缝，缝后放置一焦距为40cm的透镜，试求在透镜 焦面上出现的衍射条纹中央明纹的宽度。
夫琅禾费衍射的概念
夫琅禾费衍射的概念夫琅禾费衍射是物理学中一个重要的光学现象，它描述了光通过一个孔或一个狭缝后在远离孔或狭缝的屏上的分布情况。
夫琅禾费衍射现象的研究对于理解光的传播和干涉现象有着重要的意义。
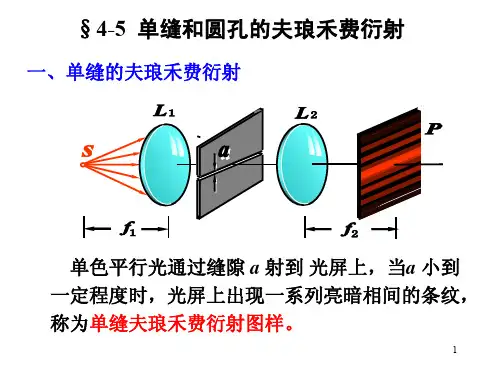
夫琅禾费衍射的基本概念可以通过一个单缝的情况来进行解释。
当单色光通过一个宽度接近光波长的狭缝时，光波会在狭缝两侧发生衍射现象。
正面入射的平行光束通过狭缝后，将呈现出圆形的衍射图样。
在远离狭缝的屏幕上观察到的图样会呈现出中央亮度较高，并且逐渐向外衰减的特点。
这个图样被称为夫琅禾费衍射图样。
夫琅禾费衍射现象可以通过赫兹斯普龙公式进行数学描述。
根据该公式，通过一个圆形孔或一个狭缝的光波将呈现出一系列同心圆环的亮暗条纹。
这些条纹的亮暗程度取决于入射光的波长、狭缝的大小以及光波与屏幕之间的距离。
当光波波长相对于狭缝宽度较大时，衍射效应将变得更加明显。
夫琅禾费衍射现象的产生可以用光波的波动性来解释。
光波通过狭缝时，会被限制在狭缝的尺寸范围内。
因此，在狭缝两端会形成波前的弯曲。
弯曲后的波前会在远离狭缝的地方重新放松，形成夫琅禾费衍射图样。
这个现象可以被视为光波的干涉效应，即不同部分的波面之间相互干涉所形成的结果。
夫琅禾费衍射现象对于光的成像和恢复过程有着广泛的应用。
在显微镜和望远镜中，通过使用透镜和光阑等光学元件可以控制夫琅禾费衍射的效果，从而使光束聚焦在被观察的目标上，并实现清晰的成像。
此外，夫琅禾费衍射现象也在光纤通信中扮演着重要的角色。
光纤中的光波会因为狭缝的存在而发生衍射，这使得光波能够在光纤内部传播。
总结起来，夫琅禾费衍射是光学中一种重要的现象，它描述了光波通过孔或狭缝后在屏幕上呈现出的衍射图样。
夫琅禾费衍射现象的研究对于理解光的传播和干涉现象具有重要的意义，也在成像和光通信等领域中有广泛应用。
对于夫琅禾费衍射的深入理解将有助于推动光学技术的发展与应用。
15.4 单缝衍射和圆孔衍射解析
2018/10/6
波动光学
2. 惠更斯—菲涅耳原理
(1) 原理内容 同一波面上的各点发出的都是相干子波. 各子波在空间某点的相干叠加，就决定了该点波的强度. (2) 原理数学表达 设初相为零, 面积为 S 的波面 Q , 其上 面元 dS 在 P 点的光振动的振幅为 Ai :
Q
n
ds
dS Ai 并与θ有关 r 面元dS 在P 点的光矢量的大小： dS 2r dE CK ( ) cos( t ) r
2018/10/6
波动光学
讨论
2 当波长越长，缝宽越小时 , 由 (1) 0 21 a 知：条纹宽度较宽，衍射效应明显.
(2) 当缝宽变大时，条纹变的窄而密集. (3) λ a 0 (4) λ a 1
0 0 波动光学退化到几何光学.
0 π
观察屏上不出现暗纹.
(5) 缝位置变化不影响条纹位置分布.
2018/10/6
波动光学
如果用望远镜观察
将该望远镜的物镜孔
到在视场中靠得很近的 径限制得更小，则可能分 辨不出这是四颗星星. 四颗星星恰能被分辨.
2018/10/6
波动光学
例：在通常亮度下，人眼的瞳孔直径约为3mm ，
视觉感受的最灵敏的光波波长为 550 nm.
求：人眼的最小分辨角为多大？ 解： 由题意有：
2018/10/6
D R 0 1.22
1
波动光学
光学仪器的分辨本领: R
1
0
D 1.22
思考：如何提高仪器分辨率？
D R
提高光学仪器
的放大倍数能提高
角分辨率吗？
望远镜： 不可选择，可 D R 显微镜： D不会很大，可 R
10章_衍射_单缝_圆孔
B
.
f
结论：分成偶数半波带为暗纹。
分成奇数半波带为明纹。
a sin k a sin ( 2k 1) 2 a sin 0
与两束光相干叠加对比
( k 1,2,) 暗纹 ( k 1,2,) 明纹 中央明纹
——无限多束子波相干叠加
(k 0,1,2,) 明纹 k (2k 1) 2 (k 0,1,2,) 暗纹
l = x k+1 x k = a
f 1 l l0 明纹中心 a 2 1) 条纹在屏幕上的位置与波长成正比，如果用白光 做光源，中央为白色明条纹，其两侧各级都为彩 色条纹。该衍射图样称为衍射光谱。
2) 缝越窄（ a 越小），条纹分散的越开，衍射现 象越明显；反之，条纹向中央靠拢。 当缝宽比波长大很多时，形成单一的明条纹，这就是 透镜形成的光源的象。显示了光的直线传播的性质。
θ 0= a
（中央亮纹半角宽度）
衍射的反比率
I
x
2f λ l 0 =2 x = a
当缝宽
（中央亮纹宽度）
中央亮纹宽度
a
l0
暗纹中心 明纹中心
3. 其它相邻两暗条纹间距（其它明纹宽度）
条纹在接收 屏上的位置
x k= ka
fλ
( k + 1) fλ x k+1= a
fλ
其它各级明条纹的宽度为中央明条纹宽度的一半。
光 的 衍 射
10-3 光的衍射
一、 光的衍射现象 惠更斯-菲涅耳原理 屏幕 屏幕
阴 影
缝较大时，光是直线传播的
缝很小时，衍射现象明显
光在传播过程中遇到障碍物，能够绕过障碍物的边缘 前进，这种偏离直线传播并形成明暗相间条纹的现象称为 光的衍射现象。
大学物理课件：10_ 4 单缝衍射和圆孔衍射
3）子波到达P点的振幅与相位符合下列四条假设
1）S 为同相面，各个子波源相位相同. 设 = 0.
2）dS发出的子波在 P 点引起的振幅与dS成正比，与 r 成反比 .
Ap d S
1
Ap r
3）dS在 P 点引起的振幅与dS的法线和 r 之间的夹角θ有关，
θ 越大，在P点的振幅越小，当θ≥(π/2)时, 振幅为零。
Ap f ( )
4) dS在 P 点引起的光振动的相位，由dS 到P点的光程 r 决定。
由菲涅耳假设可得 面元dS在P 引起的振动为:
d E( p) C f ( ) cos[t 2 r ] d S r
P点总振动的振幅：
E( p) C Σ
f ( ) cos(t 2 r ) d S
r
积分法较复杂，主要采用半波带法 。
1）明、暗条纹在屏上的位置:
P
x f tan f f sin
暗纹位置: x k f
a
a
f
x
l
o
l0
l
明纹位置： x (2k 1) f
2a
k 1,2,3,
2）明条纹宽度：
①中央明纹
线宽度
2 f
l0 a
角宽度
21
2
a
②次级明纹
f
l xk xk1 xk a
l0 2l
例题1 缝宽a = 0.5mm 的单缝后面D = 1.00 m 处置接收屏。
条纹宽度
l0
2 f
a
l0 2l
爱里斑的半角宽度： 1.22
D 光学仪器最小分辨角和分辨本领：
min
1.22
D
1
D
R
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三、入射光非垂直入射时光程差的计算
DB BC A
b(si n sin ) b
（中央明纹向下移动）
D
B
C
BC DA
b(si n sin )
（中央明纹向上移动）
D A
b
C
B
例1 在单缝衍射中，=600nm, a=0.60mm, f=60cm, 则（1）中央明纹宽度为多少？（2）两 个第三级暗纹之间的距离？
单缝和圆孔的夫琅 禾费衍射介绍
一、单缝夫琅禾费衍射
1.衍射装置及图样
单缝 透镜
衍射角
f
衍射屏
I
衍射图样
（1） 衍射条纹与狭缝平行。 （2）中心条纹很亮，两侧明条纹对称分布， 亮度减弱。 （3）中央亮斑的宽度为其他亮斑的两倍。
由惠更斯——菲涅耳原理：
单缝处波面看作无穷多个相干波源，屏上一点是 (无穷)多光束干涉的结果。
解 ⑴ 中央明纹的宽度
⑵第三级暗纹在屏上的位置
x3ftanf3a3l0
两个第三级暗纹之间的距离
x6l 7.2mm 0
例2 已知：一雷达位于路边d =15m处,射束与公路成 15°角，天线宽度a =0.20m，射束波长=30mm。
求：该雷达监视范围内公路长L =?
L
d
a
θ1
β
150
解：将雷达波束看成是单缝衍射的0级明纹
越大，
越大，衍射效应越明显.
1
二、用振幅矢量推导光强公式
1.振幅矢量法 将缝AB的面积S等分成N(很大)个等宽的窄带,
每个窄带宽度a/N.
每个窄带发的子波在P点振
A
幅近似相等，设为A1，相邻
窄带所发子波在P点引起的振
动的光程差
δ = (asin）/N
B
相位差 22asNin
屏上P点的合振幅 AP就是各子波的振幅矢量和的 模，这是多个同方向、同频率，同振幅、初相依 次差一个恒量的简谐振动的合成。
由 asin 1 有 sin 1 a3 0.2m 0m 0 m 0.15
d
a
θ1
L
β
150
1 8.63°
如图： 1° 5 1 2.6 3 ° 3
1° 5 16 .3° 7
L d (c c tg t )g
1 (5 c 6 .3 t° g 7 c2 t.6 g 3 ° ) 3 1m 00
1
sin1
a
中央明纹线宽度
x
2x12f
tg12f
a
半角宽
1
sin1
a
a
1
1
x1 x1
I
角宽度
21
2
a
f
2)其他亮纹的宽度
f
x 当较小时，
O tansin
Байду номын сангаас
屏上暗纹中心的位置：
xfta nfs i n kf k 1 ,2 ...
a
其他明纹的线宽度
其他亮纹的宽度是中央亮纹宽度的一半。
3)在 不是很小时，各级条纹的线位置为：
0
1
例5 单缝衍射中，a=0.1mm，入射波长λ=500nm，透 镜焦距f=10cm，在屏上x=1.75mm的p点为明条纹
求：（1）p点条纹级数 k?
解：由暗纹公式 a sin k，当k =1，2时有
a sin1
所以第一级暗纹衍射角
a sin2 2
1 sin1 / a
第二级暗纹衍射角
2 sin2 2 / a
所以第一级明纹角宽度
2 1 / a 0.1rad
第一级明纹线宽度
x1 f 4cm
中央明纹的线宽度
l 2x 8cm
当asin=3/2时，可将缝分为3个半波带.
a
AA
A1
p
B
A2 C
o
B /2
相邻半波带的相对应点光程差均是/2,两个
“半波带”发的光在 P处干涉相消形成暗纹。第3 个“半波带”发的光在 P形成明纹。
一般情况下，可将缝分为k个半波带，当k为偶数 时，p点为暗纹，当k为奇数时，p点为明纹。
asin0 中央明纹中心
u求)得0
du u2
得 tgu = u，由作图法可得次极大位置
y y1 = tgu
y2 = u
··
-2 - o
2 u
··
-2.46π -1.43π
+1.43π +2.46π
u 1 . 4 3 ， 2 . 4 6 ， 3 . 4 7 ， …
相应 a si n 1 .4, 3 2 .4, 6 3 .4, … 7
对于屏中心o点
衍射角为零，各子波的相位相同
A
1
…
A 0
o点的合振动振幅 A0 = N A1
中央明纹的光强 I0 A02
对于屏上其它点P，由
于屏上位置不同，对应的衍
射角就不同，Ａｐ的大小也
不同．
令 u asin
A p A i
可以求出 A A sinu 过程略
p
0u
p点的光强
I p
I 0
sinu u
例3 在单缝衍射中，若使单缝和透镜分别 稍向上移，则衍射条纹将如何变化？ 解：
o
⑴单缝上移衍射光束向上平移经透镜聚焦后， 位置不变条纹不变 ⑵透镜上移衍射光束经透镜聚焦后，位置随之 上移条纹向上平移
例4 在单缝夫琅和费衍射实验中，缝宽a=10，缝 后透镜焦距 f =40cm , 试求第一级明纹的角宽度，线 宽度以及中央明纹的线宽度。
xk ftank(k为k级条纹中k射 心角 所） 对
4)讨论：i)波长变化对条纹的影响
第一暗纹的衍射角
1
sin1
a
a一定，越大，1越大，衍射效应越明显.
一定
ii)缝宽变化对条纹的影响
a增大，1减小
a
0,1
0
a减小，1增大
a
1,1
2
光直线传播 衍射最大
单缝宽度变化，中央明纹宽度如何变化？
入射波长变化，衍射效应如何变化 ?
2
2.衍射条纹的特点 １）中央明纹
位置：在 = 0处
I p
I 0
sinu u
2
光强：中央明纹中心的光强最大 I = I0
2）暗纹
位置：在u≠0，sinu = 0处
条件: asink
sin (/a)， 2(/a)， 3(/a)，…
在sin坐标上暗纹是等间距的。
3）其他明纹
位置：由
d
sin2 (
asin2k 第k级暗纹中心 2k个半波带
2
asin(2k1) 第k级明纹中心
2
asink （介于明暗之间）
2 ( k 1,2,3,L )
2k 1
个半波带
单缝衍射的（相对）光强曲线
I
3 2
aa
a
0
2
3
sin
a
a
a
3.条纹宽度
1)中央明纹宽度：k=-1级暗纹和k=1级暗纹之间
的距离
k=1级暗纹 asin1
2.菲涅耳半波带法
f
衍射角
A
p
o
B
缝宽AB = a 称为衍射角
A→P 和 B→P的光程差 asin
0， 0—— 中央明纹(中心)
当asin=时，可将缝分为两个半波带
半波带 半波带
A
p
A1
o
相邻半波带的相对应
点光程差均是/2
B /2
相邻半波带的相对应点光程差均是/2两个
“半波带”发的光在 P处干涉相消形成暗纹。