几种常见函数的傅里叶变换及推导
- 格式:docx
- 大小:3.62 KB
- 文档页数:3

傅里叶变换常用公式推导
傅里叶变换是信号处理中非常重要的数学工具,可以将一个信号从时域转换到频域。
在信号处理和通信领域,傅里叶变换广泛应用于频谱分析、滤波、调制解调等方面。
傅里叶变换的常用公式包括正向变换和逆向变换。
正向变换将一个时域信号转换为频域信号,逆向变换则将频域信号恢复回时域信号。
首先,我们来看正向傅里叶变换的常用公式。
设时域信号为x(t),
其傅里叶变换为X(f),则公式可以表示为:
X(f) = ∫[x(t) * e^(-j2πft)] dt
其中,∫表示积分运算,e为自然对数的底数,j为虚数单位。
这个
公式表示的是在时域上的函数与指数函数的乘积的积分。
公式的意义是将时域信号分解成一系列的正弦和余弦函数,每个正弦和余弦函数对应一个频率分量。
逆向傅里叶变换则是将频域信号还原为时域信号。
设频域信号为X(f),其逆向傅里叶变换为x(t),则公式可以表示为:
x(t) = ∫[X(f) * e^(j2πft)] df
逆向傅里叶变换的公式与正向变换的公式非常相似,只是积分的变量从时间t变为频率f,并且指数函数的符号发生了变化。
这个公式的意义是将频域信号合成为一个时域信号。
傅里叶变换的常用公式还包括一些性质和定理,如平移性、尺度性、线性性等。
这些公式和定理使得傅里叶变换成为一种非常灵活和强大的工具,可以方便地对信号进行分析和处理。
总结起来,傅里叶变换的常用公式推导了信号从时域到频域的转换过程,以及从频域到时域的逆向转换过程。
这些公式和定理为信号处理和通信领域提供了重要的数学基础,使得我们可以更好地理解和分析信号。

傅里叶变换概念及公式推导傅里叶变换是一种数学工具,用于将一个函数从时域(时间域)转换为频域。
傅里叶变换的基本概念是,任何一个周期性函数都可以表示为一系列不同频率的正弦和余弦函数的叠加。
通过傅里叶变换,我们可以将原始信号分解成许多不同频率的正弦和余弦波。
F(ω) = ∫[−∞,+∞] f(t) e^(−iωt) dt其中,F(ω)表示频域中的函数,与f(t)相对应。
为了推导傅里叶变换的公式,我们首先将复数e^(−iωt)展开为正弦和余弦函数的形式:e^(−iωt) = cos(ωt) − i sin(ωt)然后将这个展开式代入变换公式中,得到:F(ω) = ∫[−∞,+∞] f(t) (cos(ωt) − i sin(ωt)) dt为了求解这个积分,我们可以利用欧拉公式,将复数表示为以指数函数的形式:F(ω) = ∫[−∞,+∞] f(t) e^(iωt) dt − i ∫[−∞,+∞] f(t) sin(ωt) dt将第一个积分的积分变量由t替换为−t,得到:F(ω) = ∫[−∞,+∞] f(t) e^(iωt) dt − i ∫[−∞,+∞] f(−t) sin(ωt) dt由于f(t)是一个偶函数(即f(−t)=f(t))F(ω) = ∫[−∞,+∞] f(t) e^(iωt) dt − i ∫[−∞,+∞] f(t)sin(ωt) dt记F(ω)的实部为Re[F(ω)],虚部为Im[F(ω)],我们可以将公式进一步简化为:Re[F(ω)] = ∫[−∞,+∞] f(t) cos(ωt) dtIm[F(ω)] = − ∫[−∞,+∞] f(t) sin(ωt) dt这就是傅里叶变换的实部和虚部的计算公式,也称为余弦分量和正弦分量的公式。
通过计算这两个积分,我们可以得到函数在不同频率上的分量。
这些频率分量相当于原始函数在频域中的表现,有助于我们理解原始函数的频率特征。
要注意的是,以上推导过程是针对连续时间信号的傅里叶变换。

常用信号的傅里叶变换傅里叶变换是一种将时域信号转换为频域信号的数学工具。
对于任意一个周期信号,傅里叶变换可以将其表示成一系列正弦波的叠加形式,从而更好地理解和处理信号。
在实际应用中,有很多信号都需要进行傅里叶变换。
下面介绍一些常用信号的傅里叶变换。
1. 正弦信号正弦信号是一种最基本的周期信号,其函数形式为y=sin(wt),其中w为角频率。
通过傅里叶变换,可以将正弦信号表示为一组频率为w的正弦波的叠加形式,即:y(t) = A1*sin(wt) + A2*sin(2wt) + A3*sin(3wt) + …其中,An为振幅,表示第n个正弦波的幅度。
2. 方波信号方波信号是一种由周期为T的矩形波形组成的信号,其函数形式为:y(t) = sgn(sin(wt))其中,sgn表示符号函数,即当sin(wt)>0时,sgn(sin(wt))=1,否则sgn(sin(wt))=-1。
通过傅里叶变换,可以将方波信号表示为一组频率为w的正弦波的叠加形式,即:y(t) = (4/pi)*[sin(wt) + (1/3)*sin(3wt) + (1/5)*sin(5wt) + …]3. 带限信号带限信号是指信号的频率范围有限,通常是指截止频率为一定值的信号。
通过傅里叶变换,可以将带限信号表示为一组频率在一定范围内的正弦波的叠加形式,即:y(t) = (1/2*pi)*Int[-w0,w0]{F(w)*e^(jwt)dw}其中,F(w)为信号的频谱,w0为信号的截止频率,Int表示积分运算。
以上三种信号只是常用信号中的一部分,实际应用中还有很多其他类型的信号需要进行傅里叶变换。
傅里叶变换不仅可以分析信号的频域特性,还可以用于信号的滤波、压缩、编码等方面,具有广泛的应用价值。

常见函数傅里叶变换傅里叶变换是一种将一个函数分解成一系列正弦和余弦函数的方法。
它是一种非常重要的数学工具,被广泛应用于信号处理、图像处理、量子力学等领域。
在本文中,我们将介绍几种常见的函数傅里叶变换。
1. 正弦函数傅里叶变换正弦函数傅里叶变换是将一个函数分解成一系列正弦函数的方法。
它适用于周期函数,即函数在一个周期内重复。
正弦函数傅里叶变换的公式为:f(x) = a0/2 + Σ(an*cos(nπx/L) + bn*sin(nπx/L))其中,a0/2是函数的平均值,an和bn是函数的傅里叶系数,L 是函数的周期。
正弦函数傅里叶变换可以用于分析周期信号的频谱特性。
2. 傅里叶级数傅里叶级数是将一个函数分解成一系列正弦和余弦函数的方法。
它适用于周期函数,即函数在一个周期内重复。
傅里叶级数的公式为:f(x) = a0/2 + Σ(an*cos(nπx/L) + bn*sin(nπx/L))其中,a0/2是函数的平均值,an和bn是函数的傅里叶系数,L是函数的周期。
傅里叶级数可以用于分析周期信号的频谱特性。
3. 傅里叶变换傅里叶变换是将一个非周期函数分解成一系列正弦和余弦函数的方法。
它适用于非周期函数,即函数在整个实数轴上都有定义。
傅里叶变换的公式为:F(ω) = ∫f(x)e^(-iωx)dx其中,F(ω)是函数的傅里叶变换,f(x)是原函数,ω是频率。
傅里叶变换可以用于分析信号的频谱特性。
4. 离散傅里叶变换离散傅里叶变换是将一个离散信号分解成一系列正弦和余弦函数的方法。
它适用于数字信号处理。
离散傅里叶变换的公式为:X(k) = Σx(n)e^(-i2πnk/N)其中,X(k)是信号的傅里叶变换,x(n)是原信号,N是信号的长度,k是频率。
离散傅里叶变换可以用于分析数字信号的频谱特性。
傅里叶变换是一种非常重要的数学工具,它可以将一个函数分解成一系列正弦和余弦函数,从而分析函数的频谱特性。
在信号处理、图像处理、量子力学等领域都有广泛的应用。

8个典型信号的傅里叶变换1. 常数信号(直流信号)这个常数信号啊,就像一个超级稳定的家伙,一直保持一个值不变。
它的傅里叶变换可有趣啦,就是一个冲激函数(狄拉克函数)在频率为0的地方。
你可以想象啊,常数信号就只有一个频率成分,那就是0频率,就像一个静止不动的状态在频率域里的表示呢。
2. 正弦信号。
正弦信号就像一个有规律的摇摆舞者。
它的傅里叶变换呢,是在正负它的角频率处有两个冲激函数。
比如说一个正弦函数Asin(ω_0t),在频率ω = ω_0和ω=-ω_0的地方有两个冲激。
这就好像在说,正弦信号就只有一个频率在那欢快地跳动,这个频率就是它自己的角频率ω_0,一正一负就像在频率轴上对称地站着两个代表它的小尖刺。
3. 余弦信号。
余弦信号跟正弦信号是近亲呢。
Acos(ω_0t)的傅里叶变换也是在正负它的角频率处有两个冲激函数。
不过和正弦信号有点小区别,就像是两个风格相似但又有点不同的舞者。
余弦信号的傅里叶变换,那两个冲激函数就像是在频率轴上标记着它自己独特的角频率ω_0的两个小灯塔。
4. 单位冲激信号(狄拉克函数)这个单位冲激信号啊,就像一个超级突然的小爆炸,瞬间爆发然后就没了。
它的傅里叶变换可神奇了,是一个常数1。
你想啊,这个小爆炸包含了所有频率成分,就像一个超级大杂烩,在频率域里就变成了一个平坦的1,就好像所有频率都被它平等对待,一股脑儿地全在里面了。
5. 矩形脉冲信号。
矩形脉冲信号就像一个突然冒出来又突然消失的小方块。
它的傅里叶变换是Aτ Sa((ωτ)/(2)),这里的A是脉冲的幅度,τ是脉冲的宽度,Sa函数是(sin x)/(x)。
这个变换就像是把矩形脉冲信号这个小方块在时间域的信息,分散到了频率域里,就像把一个集中的小方块打散成了好多频率成分,那些频率成分按照Sa函数的规律分布着。
6. 三角脉冲信号。
三角脉冲信号就像一个小山峰。
它的傅里叶变换是Aτfrac{Sa^2((ωτ)/(2))}{ω^2}。
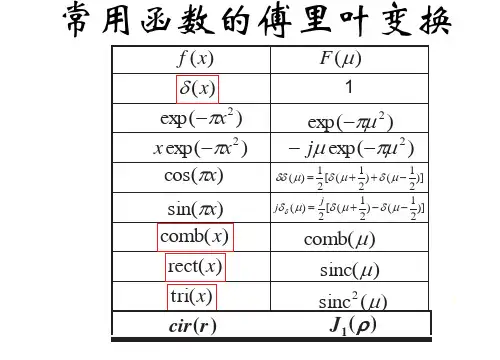
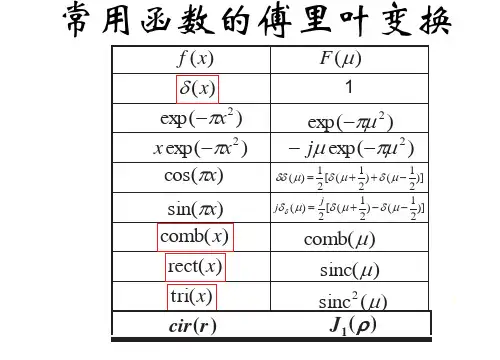

常用信号的傅里叶变换傅里叶变换是一种将信号从时域转换到频域的数学工具。
它是以法国数学家傅里叶的名字命名的,用于分析信号的频谱成分。
在信号处理和通信领域,傅里叶变换被广泛应用于信号的频谱分析、滤波、解调和压缩等方面。
1. 正弦信号的傅里叶变换正弦信号是最简单的周期信号之一,它可以表示为一个频率和幅度确定的正弦函数。
对于一个正弦信号,它的傅里叶变换是一个由两个峰值组成的频谱图。
其中一个峰值位于正弦信号的频率上,另一个峰值位于负频率上,其幅度与正弦信号的幅度相等。
2. 方波信号的傅里叶变换方波信号是一种以方波函数为基础的周期信号。
方波信号可以表示为一系列正弦信号的叠加,其傅里叶变换是一个由多个峰值组成的频谱图。
频谱图上的峰值对应于方波信号中各个频率的成分。
3. 矩形脉冲信号的傅里叶变换矩形脉冲信号是一种在有限时间内突然变化的信号。
它在时域上表现为一个宽度有限的矩形脉冲,其傅里叶变换是一个以脉冲宽度为主要参数的频谱图。
频谱图上的峰值表示了矩形脉冲信号中各个频率的成分。
4. 高斯信号的傅里叶变换高斯信号是一种以高斯函数为基础的连续非周期信号。
高斯信号在时域上呈钟形分布,其傅里叶变换是一个以高斯函数为形状的频谱图。
频谱图上的峰值表示了高斯信号中各个频率的成分。
5. 三角波信号的傅里叶变换三角波信号是一种以三角函数为基础的周期信号。
三角波信号可以表示为一系列正弦信号的叠加,其傅里叶变换是一个以基频为主要参数的频谱图。
频谱图上的峰值对应于三角波信号中各个频率的成分。
6. 音频信号的傅里叶变换音频信号是一种连续时间的信号,它可以通过傅里叶变换转换为频域信号进行分析。
音频信号的傅里叶变换可以得到音频信号的频谱图,从而可以对音频信号进行频谱分析、滤波和合成等操作。
7. 语音信号的傅里叶变换语音信号是一种声音信号,它可以通过傅里叶变换转换为频域信号进行分析。
语音信号的傅里叶变换可以得到语音信号的频谱图,从而可以对语音信号进行声音分析、语音识别和语音合成等操作。

常用函数的傅里叶变换傅里叶变换是一种将时域信号转换为频域信号的方法,常用于信号处理、通信、图像处理等领域。
在实际应用中,有很多常用的函数需要进行傅里叶变换,本文将介绍一些常用函数的傅里叶变换公式。
1. 正弦函数和余弦函数正弦函数和余弦函数是最基本的周期函数,它们的傅里叶变换公式如下:$$begin{aligned}mathcal{F}(sin(omega_0t)) &= frac{j}{2}[delta(omega-omega_0)-delta(omega+omega_0)]mathcal{F}(cos(omega_0t)) &= frac{1}{2}[delta(omega-omega_0)+delta(omega+omega_0)]end{aligned}$$其中,$omega_0$表示正弦函数和余弦函数的基频,$delta(omega)$表示狄拉克脉冲函数,$j$表示虚数单位。
2. 矩形函数矩形函数是一个限制在有限区间的常数函数,它的傅里叶变换公式如下:$$mathcal{F}(mathrm{rect}(t/T)) = Tmathrm{sinc}(omega T) $$其中,$mathrm{sinc}(x)=frac{sin(pi x)}{pi x}$为正弦积分函数。
3. 三角函数三角函数包括正弦函数、余弦函数、正切函数等,它们的傅里叶变换公式如下:$$begin{aligned}mathcal{F}(sin^2(omega_0t)) &= frac{j}{4}[delta(omega-2omega_0)-delta(omega)-delta(omega+2omega_0)]mathcal{F}(cos^2(omega_0t)) &= frac{1}{4}[delta(omega-2omega_0)+2delta(omega)+delta(omega+2omega_0)]mathcal{F}(tan(omega_0t)) &= -jfrac{pi}{2}mathrm{sgn}(omega-omega_0)-jfrac{pi}{2}mathrm{sgn}(omega+omega_0)end{aligned}$$其中,$mathrm{sgn}(x)$为符号函数。

常用fourier变换表傅里叶变换是一种重要的数学工具,常用于信号处理、图像处理、通信等领域。
以下是一些常用的傅里叶变换表:1.Fourier变换对:•时间域函数x(t) 的傅里叶变换X(f):F{ x(t) } = X(f) = ∫[−∞, +∞] x(t) * exp(-j2πft) dt•频率域函数X(f) 的傅里叶逆变换x(t):F^−1{X(f)} = x(t) = ∫[−∞, +∞] X(f) * exp(j2πft) df2.常见信号的傅里叶变换:•常数信号的傅里叶变换:F{1} = δ(f) (其中,δ(f) 表示狄拉克δ函数)•单频正弦信号的傅里叶变换:F{cos(2πf0t)} = 0.5 * [ δ(f - f0) + δ(f + f0) ]•矩形脉冲信号的傅里叶变换:F{rect(t / T)} = T * sin(πfT) / (πfT) (其中,rect(t / T) 表示矩形函数)•高斯函数的傅里叶变换:F{exp(-πt^2)} = exp(-πf^2)3.常见性质和公式:•傅里叶变换的线性性质:F{a * x(t) + b * y(t)} = a * X(f) + b * Y(f)•频率平移性质:F{ x(t - t0) } = X(f) * exp(-j2πft0)•时域和频域的缩放性质:F{ x(a * t) } = (1 / |a|) * X(f / a)•卷积定理:F{ x(t) * y(t) } = X(f) * Y(f) (其中* 表示卷积操作)这些是一些常见的傅里叶变换表中的内容,可以帮助我们理解信号在时域和频域之间的关系,进而应用到实际问题的分析和处理中。
请注意,这里只给出了部分常见的表达式和性质,实际的傅里叶变换表还包含更多的公式和变换对,具体的应用需要根据具体问题进行深入研究和理解。

五种傅里叶变换解析标题:从简到繁:五种傅里叶变换解析引言:傅里叶变换是数学中一种重要且广泛应用于信号处理、图像处理和物理等领域的工具。
它的基本思想是将一个信号或函数表示为若干个不同频率的正弦波的叠加,从而揭示信号或函数的频谱特性。
本文将展示五种常见的傅里叶变换方法,包括离散傅里叶变换(DFT)、快速傅里叶变换(FFT)、连续傅里叶变换(CTFT)、离散时间傅里叶变换(DTFT)和傅里叶级数展开,帮助读者逐步理解傅里叶变换的原理与应用。
第一部分:离散傅里叶变换(DFT)在此部分中,我们将介绍离散傅里叶变换的基本概念和算法。
我们将讨论DFT的离散性质、频域和时域之间的关系,以及如何利用DFT进行频域分析和滤波等应用。
此外,我们还将探讨DFT算法的时间复杂度,以及如何使用DFT来解决实际问题。
第二部分:快速傅里叶变换(FFT)在这一部分中,我们将深入研究快速傅里叶变换算法,并详细介绍其原理和应用。
我们将解释FFT如何通过减少计算量和优化计算过程来提高傅里叶变换的效率。
我们还将讨论FFT算法的时间复杂度和几种不同的FFT变体。
第三部分:连续傅里叶变换(CTFT)本部分将介绍连续傅里叶变换的概念和定义。
我们将讨论CTFT的性质、逆变换和时频分析的应用。
进一步,我们将引入傅里叶变换对信号周期性的描述,以及如何利用CTFT对信号进行频谱分析和滤波。
第四部分:离散时间傅里叶变换(DTFT)在这一章节中,我们将介绍离散时间傅里叶变换的基本原理和应用。
我们将详细讨论DTFT的定义、性质以及与DFT之间的关系。
我们还将探讨DTFT的离散频率响应、滤波和频谱分析的相关内容。
第五部分:傅里叶级数展开最后,我们将深入研究傅里叶级数展开的原理和应用。
我们将解释傅里叶级数展开如何将周期函数分解为多个不同频率的正弦波的叠加。
我们还将讨论傅里叶级数展开的收敛性和逼近性,并探讨如何利用傅里叶级数展开来处理周期信号和周期性问题。
结论:综上所述,本文介绍了五种常见的傅里叶变换方法,包括离散傅里叶变换(DFT)、快速傅里叶变换(FFT)、连续傅里叶变换(CTFT)、离散时间傅里叶变换(DTFT)和傅里叶级数展开。
常用傅里叶变换公式大全傅里叶变换是一种重要的数学工具,它可以将时域信号转换为频域信号,从而更好地理解信号的特性。
下面就是常用的傅里叶变换公式大全:1、傅里叶变换:$$F(u)=\int_{-\infty}^{\infty}f(x)e^{-2\pi iux}dx$$2、傅里叶反变换:$$f(x)=\int_{-\infty}^{\infty}F(u)e^{2\pi iux}du$$3、离散傅里叶变换:$$F(u)=\sum_{n=-\infty}^{\infty}f(n)e^{-2\pi iun}$$4、离散傅里叶反变换:$$f(n)=\frac{1}{N}\sum_{u=-\infty}^{\infty}F(u)e^{2\pi iun}$$5、快速傅里叶变换:$$F(u)=\sum_{n=0}^{N-1}f(n)W_N^{nu}$$6、快速傅里叶反变换:$$f(n)=\frac{1}{N}\sum_{u=0}^{N-1}F(u)W_N^{-nu}$$7、离散余弦变换:$$F(u)=\sum_{n=0}^{N-1}f(n)\cos\frac{(2n+1)u\pi}{2N}$$8、离散余弦反变换:$$f(n)=\frac{1}{N}\sum_{u=0}^{N-1}F(u)\cos\frac{(2n+1)u\pi}{2N}$$9、离散正弦变换:$$F(u)=\sum_{n=0}^{N-1}f(n)\sin\frac{(2n+1)u\pi}{2N}$$10、离散正弦反变换:$$f(n)=\frac{1}{N}\sum_{u=0}^{N-1}F(u)\sin\frac{(2n+1)u\pi}{2N}$$以上就是常用的傅里叶变换公式大全,它们可以帮助我们更好地理解信号的特性,并且可以用来解决许多实际问题。
因此,傅里叶变换在科学研究和工程应用中都有着重要的作用。
常用信号的傅里叶变换
傅里叶变换是一种将函数从时域(时间域)转换到频域(频率域)的数学技术。
在信号处理中,傅里叶变换可以用来分析各种信号的频率成分。
下面是一些常见信号的傅里叶变换:
1. 正弦信号:正弦信号是基本的周期信号,其傅里叶变换是两个峰值的Delta函数,分别位于正负频率轴上。
峰值的高度与正弦信号的振幅成正比。
2. 方波信号:方波信号的傅里叶变换是一系列的Delta函数,位于基频和其倍频的频率轴上。
每个Delta函数的幅值与方波的斜率成正比。
3. 三角波信号:三角波信号的傅里叶变换是一系列的Delta函数,位于基频和其奇倍频的频率轴上。
每个Delta函数的幅值与三角波的斜率成正比,而且随着频率的增加而逐渐减小。
4. 窗函数信号:窗函数信号可以用来限制一个信号的频率范围。
常见的窗函数信号有矩形窗、汉宁窗、汉明窗等。
它们的傅里叶变换都是一系列的Delta函数,位于基频和其倍频的频率轴上。
不同的窗函数有不同的幅值分布。
5. 常见滤波器的傅里叶变换:滤波器可以用来去除一个信号的某些频率成分。
常见的滤波器有低通滤波器、高通滤波器、带通滤波器、带阻滤波器等。
它们的傅里叶变换都有不同的频率响应曲线,用来描述信号在不同频率上的响应情况。
以上是一些常见信号的傅里叶变换,它们可以用来分析和处理各
种实际的信号。
在实际应用中,傅里叶变换经常和其它技术一起使用,如滤波、采样、量化等,以实现更复杂的信号处理任务。
常见函数的傅里叶变换傅里叶变换是一种将一个函数映射到频域的数学工具。
通过它,我们可以将一个信号或者一个函数进行频域分析,对其进行处理、滤波、特征提取等。
在信号处理、图像处理、通信等领域中,傅里叶变换非常重要。
本文将介绍几种常见的函数的傅里叶变换及其应用。
一、常数函数常数函数f(x)=c,其中c为常数,其傅里叶变换为:F(k)=c\int_{-\infty}^\infty e^{-2\piikx}dx=c\delta(k)其中\delta(k)是狄拉克δ 函数,表示在k=0时存在一个单位脉冲。
显然,常数函数的傅里叶变换是一个单位脉冲。
在实际应用中,常数函数的傅里叶变换用于求解不同函数的卷积。
二、正弦函数正弦函数f(x)=sin(2πwx),其傅里叶变换为:F(k)=\int_{-\infty}^\infty sin(2\pi wx)e^{-2\pi ikx}dx=-\frac{iw}{2} (\delta(k-w)+\delta(k+w))正弦函数的傅里叶变换具有许多实用性质,例如:1. 它反映了信号在频域中的分布,即将正弦函数分解成不同频率的正弦函数的和。
2. 它可以用来提取频率信息。
3. 它还可以用来滤波。
三、余弦函数余弦函数f(x)=cos(2πwx),其傅里叶变换为:F(k)=\int_{-\infty}^\infty cos(2\pi wx)e^{-2\pi ikx}dx=\frac{w}{2} (\delta(k-w)+\delta(k+w))与正弦函数相似,余弦函数也可以用来分解信号,并且可以用来提取频率信息和滤波。
四、矩形脉冲函数矩形脉冲函数f(x)=rect(x)(即在[-0.5, 0.5]内为1,在其他地方为0),其傅里叶变换为:F(k)=\int_{-\infty}^\infty rect(x)e^{-2\piikx}dx=\int_{-0.5}^{0.5}e^{-2\piikx}dx=\frac{sin(\pi kw)}{\pi kw}矩形脉冲函数的傅里叶变换也称为sinc函数。
常用傅里叶变换表在数学和工程领域,傅里叶变换是一种非常重要的工具,它能够将一个时域信号转换为频域表示,从而帮助我们更好地理解和处理各种信号。
为了方便使用,人们总结出了常用的傅里叶变换表。
傅里叶变换的基本概念是将一个函数表示为不同频率的正弦和余弦函数的线性组合。
通过这种变换,我们可以从不同的角度分析信号的特性,例如频率成分、能量分布等。
常见的函数及其傅里叶变换如下:1、单位冲激函数(δ函数)单位冲激函数在时域中是一个在某一时刻瞬间出现的极大值,而在其他时刻为零。
它的傅里叶变换是常数 1。
2、单位阶跃函数单位阶跃函数在时域中从某一时刻开始值为 1。
其傅里叶变换为 1 /(jω) +πδ(ω) 。
3、正弦函数正弦函数sin(ω₀t) 的傅里叶变换为π δ(ω ω₀) δ(ω +ω₀) 。
4、余弦函数余弦函数cos(ω₀t) 的傅里叶变换为π δ(ω ω₀) +δ(ω +ω₀) 。
5、指数函数指数函数 e^(αt) u(t) (其中 u(t) 为单位阶跃函数,α > 0)的傅里叶变换为 1 /(α +jω) 。
6、矩形脉冲函数矩形脉冲函数在一定区间内值为 1,其他区间为 0。
其傅里叶变换可以通过计算得到特定的表达式。
这些只是傅里叶变换表中的一部分常见函数。
在实际应用中,我们常常需要对复杂的信号进行傅里叶变换。
通过将复杂信号分解为上述常见函数的组合,再利用傅里叶变换的线性性质(即多个函数之和的傅里叶变换等于各个函数傅里叶变换之和),可以方便地求出复杂信号的频域表示。
傅里叶变换在许多领域都有广泛的应用。
在通信领域,它用于信号的调制和解调、频谱分析等。
在图像处理中,傅里叶变换可以帮助我们分析图像的频率特性,从而进行图像增强、滤波等操作。
在控制系统中,它可以用于分析系统的频率响应,帮助设计控制器。
例如,在音频处理中,我们可以通过傅里叶变换将声音信号从时域转换到频域,从而识别出不同的频率成分,实现音频的滤波、降噪等处理。
五种傅里叶变换解析标题:深入解析五种傅里叶变换引言:傅里叶变换是一种重要的数学工具,它在信号处理、图像处理、频谱分析等领域发挥着重要的作用。
其中,傅里叶级数、离散傅里叶变换、傅里叶变换、快速傅里叶变换和短时傅里叶变换是五种常见的傅里叶变换方法。
在本文中,我们将深入解析这五种傅里叶变换的原理和应用,以帮助读者更全面、深刻地理解它们。
1. 傅里叶级数:1.1 傅里叶级数的基本概念和原理1.2 傅里叶级数在信号分析中的应用案例1.3 对傅里叶级数的理解和观点2. 离散傅里叶变换:2.1 离散傅里叶变换的基本原理和离散化方法2.2 离散傅里叶变换在数字信号处理中的应用案例2.3 对离散傅里叶变换的理解和观点3. 傅里叶变换:3.1 傅里叶变换的定义和性质3.2 傅里叶变换在频谱分析中的应用案例3.3 对傅里叶变换的理解和观点4. 快速傅里叶变换:4.1 快速傅里叶变换的算法和优势4.2 快速傅里叶变换在图像处理中的应用案例4.3 对快速傅里叶变换的理解和观点5. 短时傅里叶变换:5.1 短时傅里叶变换的原理和窗函数选择5.2 短时傅里叶变换在语音处理中的应用案例5.3 对短时傅里叶变换的理解和观点总结与回顾:通过对五种傅里叶变换的深入解析,我们可以看到它们在不同领域的广泛应用和重要性。
傅里叶级数用于对周期信号进行分析,离散傅里叶变换在数字信号处理中具有重要地位,傅里叶变换常用于频谱分析,快速傅里叶变换作为计算效率更高的算法被广泛采用,而短时傅里叶变换在时变信号分析中展现出其优势。
对于读者而言,通过深入理解这五种傅里叶变换的原理和应用,可以更好地应用它们解决实际问题。
观点和理解:从简到繁、由浅入深地探讨五种傅里叶变换是为了确保读者能够从基础开始逐步理解,从而更深入地理解其运算原理、应用场景和优缺点。
通过结构化的文章格式,读者可以清晰地了解到每种傅里叶变换的特点和优势,并能够进行比较和评估。
同时,本文在总结与回顾部分提供了对这五种傅里叶变换的综合理解,以帮助读者获得更全面、深刻和灵活的知识。
典型函数傅里叶变换推导一、傅里叶级数的引入任何一个周期函数都可以用一组正弦函数或余弦函数的线性组合来表示,这就是傅里叶级数的基本思想。
假设有一个周期为T的函数f(t),它可以表示为:f(t) = a0 + Σ(an*cos(nωt) + bn*sin(nωt)),其中an和bn是系数,n是正整数,ω是角频率,a0是直流分量。
这就是傅里叶级数展开式。
二、傅里叶变换的定义傅里叶变换是将一个函数从时域转换到频域的过程,它将一个函数f(t)变换为另一个函数F(ω),表示函数在不同频率下的成分。
傅里叶变换的定义如下:F(ω) = ∫[f(t)*e^(-jωt)]dt,其中e^(-jωt)是欧拉公式,表示角频率ωt的复指数。
傅里叶变换将函数f(t)在时域的信息转换为频域的信息。
三、傅里叶变换的推导为了推导傅里叶变换,我们先考虑一个非周期函数f(t),它可以表示为一个周期为T的函数的展开式的极限形式:f(t) = lim[T->∞]{Σ[An*cos(nωt) + Bn*sin(nωt)]},其中An和Bn是系数,n是正整数,ω是角频率。
将上式代入傅里叶变换的定义中,得到:F(ω) = ∫[lim[T->∞]{Σ[An*cos(nωt) + Bn*sin(nωt)]}*e^(-jωt)]dt。
由于f(t)是非周期函数,所以对于不同的角频率ω,展开式中每一项的系数An和Bn都可能不同。
为了简化计算,我们引入复指数形式的傅里叶级数展开式:f(t) = Σ[Cn*e^(jωnt)],其中Cn是系数,n是整数。
将上式代入傅里叶变换的定义中,得到:F(ω) = ∫[Σ[Cn*e^(jωnt)]*e^(-jωt)]dt。
利用欧拉公式,将上式展开为实部和虚部的形式:F(ω) = ∫[Σ[Cn*(cos(nωt) + jsin(nωt))]*e^(-jωt)]dt。
对上式中的每一项进行积分,得到:F(ω) = Σ[Cn*∫[e^(-jωt + jnωt)]dt]。
几种常见函数的傅里叶变换及推导
傅里叶变换是数学中一种非常重要的变换方法,它可以将一个函数在时域(或空域)中的表达转换为频域中的表达。
在信号处理、图像处理、通信等领域中被广泛应用。
本文将介绍几种常见函数的傅里叶变换及推导过程。
1. 方波函数的傅里叶变换
方波函数是一种周期函数,它在每个周期内以不同的幅度交替出现。
方波函数的傅里叶变换可以通过将方波函数表示为一系列正弦函数的和来推导得到。
假设方波函数为f(t),其周期为T,傅里叶变换为F(ω)。
根据傅里叶级数展开的性质,方波函数可以表示为:
f(t) = (1/2) + (2/π)sin(ωt) + (2/π)sin(2ωt) + (2/π)sin(3ωt) + ...
其中,ω = 2π/T是方波函数的角频率。
根据傅里叶变换的定义,可以得到方波函数的傅里叶变换为:
F(ω) = (1/2)δ(ω) + (1/2π)[δ(ω-ω0) - δ(ω+ω0)] + (1/2π)[δ(ω-2ω0) - δ(ω+2ω0)] + (1/2π)[δ(ω-3ω0) - δ(ω+3ω0)] + ...
其中,δ(ω)是狄拉克函数,表示单位冲激函数。
傅里叶变换的结果是一系列的冲激函数,每个冲激函数对应一个正弦函数的频谱分量。
2. 高斯函数的傅里叶变换
高斯函数是一种常用的连续函数,其在数学和物理学中有广泛的应用。
高斯函数的傅里叶变换可以通过将高斯函数表示为指数函数的平方和来推导得到。
假设高斯函数为f(t),傅里叶变换为F(ω)。
根据高斯函数的定义,可以得到:
f(t) = e^(-αt^2)
其中,α是常数。
根据傅里叶变换的定义,可以得到高斯函数的傅里叶变换为:
F(ω) = √(π/α)e^(-ω^2/(4α))
高斯函数的傅里叶变换仍然是一个高斯函数,只是幅度和频率发生了变化。
3. 矩形函数的傅里叶变换
矩形函数是一种常见的函数,它在一个有限区间内的值为常数,而在其他区间内的值为零。
矩形函数的傅里叶变换可以通过将矩形函数表示为两个单位阶跃函数的差来推导得到。
假设矩形函数为f(t),其宽度为2a,傅里叶变换为F(ω)。
根据矩形函数的定义,可以得到:
f(t) = 1,-a≤t≤a
= 0,其他
其中,a是常数。
根据傅里叶变换的定义,可以得到矩形函数的傅里叶变换为:
F(ω) = (2a/ω)sin(ωa)
矩形函数的傅里叶变换是一个正弦函数,其频率和幅度与矩形函数的宽度有关。
本文介绍了几种常见函数的傅里叶变换及推导过程。
方波函数、高斯函数和矩形函数分别展示了不同类型函数的傅里叶变换结果。
傅里叶变换在信号处理和频谱分析中具有重要的应用价值,通过对函数在频域中的表示,可以更好地理解和处理信号的特性。
希望本文对读者有所启发,对傅里叶变换的理解有所帮助。