24.1-24.2与圆的位置关系水平测试卷

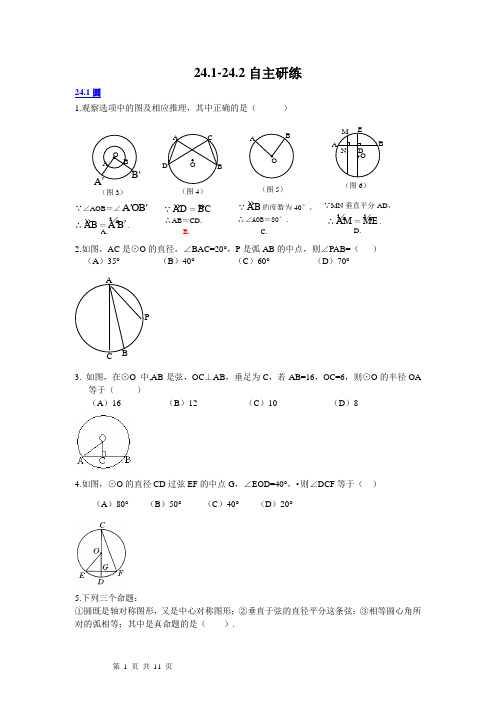
5.下列三个命题：①圆既是轴对称图形，对的弧相等；其中是真命题的是（（A）①②（B）②③（C）①③（D）①②③6.如图，AB是⊙O的直径，点C在⊙O上，∠B=70°，则∠A的度数是（）（A）20°（B）25°（C）30°（D）35°7.如图，A、B、C是⊙O上的三点，∠BAC=45°，则∠BOC•的大小是（）（A）90°（B）60°（C）45°（D）22．5°8.如图，AB是⊙O的直径，BC、CD、DA是⊙O的弦，且BC=CD=•DA，则∠BCD=（）（A）100°（B）110°（C）120°（D）135°9. 已知⊙O中最长的弦为16cm，则⊙O的半径为________cm．10. 弦AB把圆分成1：3两部分，则AB所对的劣弧等于_______度，AB•所对的优弧等于________度．11.如图，水平放置的一个油管的截面半径为13cm，其中有油部分油面宽AB为24cm，则截面上有油部分油面高CD(单位：cm)为_______________.12.如图，△ABC为⊙O的内接三角形，AB为⊙O的直径，点D•在⊙O 上，∠BAC=35°，则∠ADC=_______度．13. 如图，方格纸上一圆经过（2，6）、（-2，2）、（2，-2）、（6，2）四点，•则该圆圆心的坐14. 如图所示，已知C 为 AB •则CD=_______．BC ADO NM（保留作图痕迹，不写作法）OBA=30°，•点D的4.如图，⊙O的半径OC=5cm则1沿OC所在直线向下平移（A）1 （5.如果两圆外切，那么它们的公切线的条数为（13.如图，已知直线CD等于_______（度）．14.若半径为3cm 和4cm●备用题：两圆的直径分别是15.已知圆心在y轴17.如图，A是⊙O外一点，B是⊙O上一点，∠C=22．5°，∠A=45°．求证：直线AB是⊙上一点，DE⊥AB于点H，满足什么条件时，PC与⊙O测得钢球顶点连结OC、BC,则有与⊙O相交于C1、C2两∵OB、OC是⊙O的半径，∴∴∠OBC=∠OCB=22∴∠AOB=∠OBC+∠∵∠A=45°．∴∠OBA=180°-（∠。

达标训练基础·巩固·达标1．若⊙A 的半径为5，点A 的坐标为（3，4），点P 的坐标为（5，8），则点P( ) A.在⊙A 内 B.在⊙A 上 C.在⊙A 外 D.提示：本题两种方法，既可以画图，也可以计算A P 的长.∵A P=()()204248352222＝＝+-+-＜5，所以点P 在圆内.答案：A2．圆心为O 的甲、乙两圆，半径分别为r 1和r 2，且r 1＜OA ＜r 2，那么点A( )A.甲圆内B.乙圆外C.甲圆外，乙圆内D.提示：点A 在两圆组成的圆环内.答案：C3．已知⊙O 的半径为3.6 cm ，线段OA =257 cm ，则点A 与⊙O 的位置关系是( )A.A 点在⊙OB.A 点在⊙OC.A 点在⊙OD.提示：用“点到圆心的距离d 与半径r 的大小关系”来判定点与圆的位置关系.答案：C4．⊙O 的半径为5，圆心O 的坐标为（0，0），点P 的坐标为（4，2），则点P 与⊙O( )A.点P 在⊙OB.点P 在⊙OC.点P 在⊙OD.点P 在⊙O 上或⊙O提示：比较O P 与半径r 的关系.∵O P=５＝22422+，O P 2=20. ∵r 2=25，∴O P ＜r.∴点P 在⊙O 内.答案：A5．在△ABC 中，∠C =90°，AC =BC =4 cm ，D 是AB 边的中点，以C 为圆心，4 cm 长为半径作圆，则A 、B 、C 、D 四点中在圆内的有( ) A.1 B.2 C.3 D.4提示：如右图，连接CD .∵D 为AB 的中点，∴CD =21AB .∵AB =24BC AC 22=+，∴CD =22＜4.∵AC =BC =4C 和点D 在以C 为圆心，4 cm的圆的内部.答案：B6．已知a 、b 、c 是△ABC 三边长，外接圆的圆心在△ABC ( )A.a =15，b =12，c =1 B.a =5，b =12，c =12C.a =5，b =12，c =13D.a =5，b =12，c =14 提示：只有直角三角形的外心在边上（斜边中点）.答案：C7．在R t △ABC 中，∠C =90°，AC =6 cm ，BC =8 cm ，则它的外心与顶点C ( ) A.5cm B.6 cmC.7 cmD.8 cm提示：AB =2286 =10，它的外心是斜边中点，外心与顶点C 的距离是斜边的中线长为21AB =5 cm. 答案：A8.点A 在以O 为圆心，3 cm 为半径的⊙O 内，则点A 到圆心O 的距离d 的范围是_________.提示：根据点和圆的位置关系判定.答案：0≤d ＜39．如图24-2-5，在△ABC 中，∠ACB =90°，AC =2 cm ，BC =4 cm ，CM 为中线，以C 为圆心，5 cm 为半径作圆，则A 、B 、C 、M 四点在圆外的有_________，在圆上的有________，在圆内的有__________.图24-2-5提示：AB =25 cm ，C M=5 cm.答案：点B 点M 点A 、C10.已知圆的半径等于5 cm ，根据下列点P 到圆心的距离：（1）4 cm ；（2）5 cm ；（3）6 cm ，判定点P 与圆的位置关系，并说明理由.提示：利用点与圆的位置关系，由点到圆心距离与半径的大小比较.解：（1）当d=4 cm 时，∵d ＜r ，∴点P 在圆内.（2）当d=5 cm 时，∵d=r ，∴点P 在圆上.（3）当d=6 cm 时，∵d ＞r ，∴点P 在圆外.综合·应用·创新11．（经典回放）阅读下面材料：对于平面图形A ，如果存在一个圆，使图形A 上的任意一点到圆心的距离都不大于这个圆的半径，则称图形A 被这个圆所覆盖.图24-2-6①中的三角形被一个圆所覆盖，图24-2-6②中的四边形被两个圆所覆盖.图24-2-6（1）边长为1 cm 的正方形被一个半径为r 的圆所覆盖，r 的最小值是________cm （2）边长为1 cm 的等边三角形被一个半径为r 的圆所覆盖，r 的最小值是________cm ；（3）边长为2 cm ，1 cm 的矩形被两个半径都为r 的图所覆盖，r 的最小值是_________cm ，这两个圆的圆心距是____________cm .提示：图形被圆覆盖，圆一定大于图形的外接圆，它的最小半径就是外接圆半径.解：（1）正方形的外接圆半径，是对角线的一半，因此r 的最小值是22 cm.（2）等边三角形的外接圆半径是其高的23，故r 的最小值是33 cm. （3）r 的最小值是22 c m ，圆心距是1 cm.答案：（1）22 （2）33 （3）22 1 12.已知R t △ABC 的两直角边为a 和b ，且a 、b 是方程x 2-3x ＋1=0的两根，求R t △ABC积.提示：由a 、b 是直角三角形的两直角边，所以可求出斜边是22b a +，这样就得外接圆半径.根据直角三角形的外心是斜边中点，因此，其外接圆直径就是直角三角形的斜边.解：设Rt △ABC 的斜边为c ，∵a 、b 为方程x 2-3x ＋1=0∴a ＋b=3ab=1.由勾股定理，得c 2=a 2＋b 2=（a ＋b ）2-2ab=9-2=7.∴△ABC 的外接圆面积S=π·22⎪⎭⎫ ⎝⎛c =π∏=⨯∏=∏=47744422c c . 回顾·热身·展望13．（湖南常德模拟）有一个未知圆心的圆形工件（如图24-2-7）.现只允许用一块直角三角板（注：不允许用三角板上的刻度）画出该工件表面上的一根直径并定出圆心.要求在图上保留画图痕迹，写出画法.图24-2-7提示：因为三角板有一个角是直角，所以可利用直角画90°的圆周角，由此可得直径，再画一个90°的圆周角，也能得到一直径，两直径的交点为圆心.答案：画法：(1)用三角板的直角画圆周角∠BDC =90°，∠EF H=90(2)连接BC 、E H ，它们交于点O .BC 为直径，点O 为圆心.14.（经典回放）电脑CP U 芯片由一种叫“单晶硅”的材料制成，未切割前的单晶硅材料是一种薄圆形片，叫“晶圆片” .现在为了生产某种CP U 芯片，需要长、宽都是1 cm 的正方形小硅片若干，如图24-2-8所示.如果晶圆片的直径为10.05 cm ，问一张这种晶圆片能否切割出所需尺寸的小硅片66张？请说明你的方法和理由.图24-2-8答案：可以切割出66个小正方形.方法一：（1）我们把10个小正方形排成一排，看成一个的矩形，这个矩形刚好能放入直径为10.05 m.题图中矩形ABCD .∵AB =1，BC =10，∴对角线AC 2=100＋1=101＜（10.05）2.（2）我们在矩形ABCD 的上方和下方可以分别放入9个小正方形.∵新加入的两排小正方形连同ABCD 的一部分可看成矩形EF GH矩形EF GH 的长为9，高为3，对角线E G 2=92＋32=81＋9＜（10.05）2，但是新加入的这两排小正方形不能每排10个，因为：102＋32=100＋9＞（10.05）2.（3）同理，∵82＋52=64＋25＜（10.05）2，92＋52=81＋25=106＞（10.05）2，∴可以在矩形EF GH 的上面和下面分别再排下8个小正方形，那么现在小正方形已有了5层.（4）再在原来的基础上，上下再加一层，共7层，新矩形的高可以看成是7，那么新加入的这两排，每排可以是7个，但不能是8个.∵72＋72=49＋49=98＜（10.05）2，82＋72=64＋49=113＞（10.05）2.（5）在第7层的基础上，上下再加一层，新矩形的高可以看成是9，这两层每排可以是4个，但不能是5个.∵42＋92=16＋81=97＜（10.05）2，52＋92=25＋81=106＞（10.05）2.现在总共排了9层，高度达到了9，上下各剩下约0.5 cm ABCD置不能调整，故再也放不下一个小正方形了.所以10＋2×9＋2×8＋2×7＋2×4=66（个）.。

前言：
该测试题由多位一线国家特级教师针对当前最新的热点、考点、重点、难点、知识点，精心编辑而成。

以高质量的测试题助力考生查漏补缺，在原有基础上更进一步。

（最新精品测试题）
24.2 点和圆、直线和圆的位置关系
24．2.1 点和圆的位置关系
1．已知⊙O的半径为5 cm，点P为⊙O外一点，则OP的长可能是( ) A．5 cm B．4 cm
C．3 cm D．6 cm
2．三角形的外心是三角形的( )
A．三条中线的交点
B．三条高的交点
C．三条角平分线的交点
D．三条边的垂直平分线的交点
3．已知⊙O的半径为10 cm，点P到圆心的距离为d.
(1)当d＝8 cm时，点P在⊙O____；
(2)当d＝10 cm时，点P在⊙O____；
(3)当d＝12 cm时，点P在⊙O____.
4．如图24­2­3，在矩形ABCD中，AB＝4，AD＝3，以顶点D为圆心作半径为r的圆，若要求另外三个顶点A，B，C中至少有一个点在圆内，且至少有一个点在圆外，则r的取值范围是____．
图24­2­ 3
5．已知A，B，C三点，根据下列条件，说明A，B，C三点能否确定一个圆．如果能，求出圆的半径；如果不能，请说明理由．
1。

人教版 九年级数学上册 24.1 --24.4分节测试题含答案） 24.1 圆的有关性质一、选择题（本大题共10道小题）1. 如图所示的圆规，点A 是铁尖的端点，点B 是铅笔芯尖的端点，已知点A 与点B 的距离是2 cm ，若铁尖的端点A 固定，将铅笔芯尖的端点B 绕点A 旋转一周，则作出的圆的直径是( )A ．1 cmB ．2 cmC ．4 cmD ．π cm2. 如图，AB是⊙O 的直径，弦CD ⊥AB 于点E ，则下列结论正确的是( )A ．OE ＝BEB.BC ︵＝BD ︵ C ．△BOC 是等边三角形D ．四边形ODBC 是菱形3. 如图，AB是⊙O 的直径，BC ︵＝CD ︵＝DE ︵，∠COD ＝34°，则∠AEO 的度数是( )A ．51°B ．56°C ．68°D ．78°4. 如图，OA是⊙O 的半径，B 为OA 上一点(不与点O ，A 重合)，过点B 作OA的垂线交⊙O 于点C .以OB ，BC 为边作矩形OBCD ，连接BD .若BD ＝10，BC ＝8，则AB 的长为( )A ．8B ．6C ．4D ．25. 在⊙O 中，圆心角∠AOB ＝3∠COD (∠COD <60°)，则劣弧AB ，劣弧CD 的大小关系是( ) A.AB ︵＝3CD ︵B.AB ︵>3CD ︵C.AB ︵<3CD ︵D ．3AB ︵<CD ︵6. 如图，将半径为2的圆形纸片折叠后，圆弧恰好经过圆心O ，则折痕AB 的长为( )A. 5 B ．2 5 C ．3 D ．2 37. 如图，AB 是⊙O的直径，弦CD ⊥AB 于点E.若AB ＝8，AE ＝1，则弦CD 的长是( )A.7 B ．27 C ．6 D ．88. 如图，直线l1∥l2，以直线l1上的点A 为圆心、适当长为半径画弧，分别交直线l1，l2于点B ，C ，连接AC ，BC.若∠ABC ＝54°，则∠1等于( )A ．36°B ．54°C ．72°D ．73°9. 如图，在⊙O 中，AB ︵所对的圆周角∠ACB ＝50°，若P 为AB︵上一点，∠AOP ＝55°，则∠POB 的度数为( )A ．30°B ．45°C ．55°D ．60°10. 如图，△ABC 是⊙O 的内接三角形，∠C ＝30°，⊙O 的半径为5.若P 是⊙O上的一点，在△ABP 中，PB ＝AB ，则PA 的长为( )A ．5 B.5 32C ．5 2D ．5 3二、填空题（本大题共8道小题） 11. 2018·孝感 已知⊙O 的半径为10 cm ，AB ，CD 是⊙O 的两条弦，AB ∥CD ，AB ＝16 cm ，CD ＝12 cm ，则弦AB 和CD 之间的距离是________cm.12. 2018·毕节如图，AB 是⊙O 的直径，C ，D 为半圆的三等分点，CE ⊥AB 于点E ，则∠ACE 的度数为________．13. 如图，平面直角坐标系xOy 中，点M 的坐标为(3，0)，⊙M 的半径为2，过点M 的直线与⊙M 的交点分别为A ，B ，则△AOB 的面积的最大值为________，此时A ，B 两点所在直线与x 轴的夹角等于________°.14. 如图所示，OB ，OC是⊙O 的半径，A 是⊙O 上一点．若∠B ＝20°，∠C ＝30°，则∠A ＝________°.15. 如图，⊙O 的直径AB 过弦CD 的中点E ，若∠C ＝25°，则∠D ＝________°.16. 如图所示，动点C 在⊙O 的弦AB 上运动，AB ＝23，连接OC ，过点C 作CD ⊥OC 交⊙O 于点D ，则CD 的最大值为________．17. 如图，圆内接四边形ABCD 中两组对边的延长线分别相交于点E ，F ，且∠A＝55°，∠E ＝30°，则∠F ＝________°.18. 如图所示，在半圆O 中，AB为直径，P 为AB ︵的中点，分别在AP ︵和PB ︵上取其中点A 1和B 1，再在P A ︵1和PB ︵1上分别取其中点A 2和B 2.若一直这样取下去，则∠A n OB n ＝________°.三、解答题（本大题共4道小题）19. 如图，在△ABC 中，∠C ＝90°，D 是BC 边上一点，以BD 为直径的⊙O 经过AB 的中点E ，交AD 的延长线于点F ，连接EF. (1)求证：∠1＝∠F ；(2)若AC ＝4，EF ＝2 5，求CD 的长．20.如图，△ABC 和△ABD 都是直角三角形，且∠C ＝∠D ＝90°.求证：A ，B ，C ，D 四点在同一个圆上.21. (2019•包头)如图，在⊙O 中，B 是⊙O 上的一点，120ABC ∠=︒，弦AC =弦BM 平分ABC ∠交AC 于点D ，连接MA MC ，． (1)求⊙O 半径的长； (2)求证：AB BC BM +=．22. 如图，已知AB 为⊙O 的直径，C 为半圆ACB ︵上的动点(不与点A ，B 重合)，过点C 作弦CD ⊥AB ，∠OCD 的平分线交⊙O 于点P ，则点P 的位置有何规律？请证明你的结论．人教版 九年级数学 24.1 圆的有关性质-答案一、选择题（本大题共10道小题） 1. 【答案】C2. 【答案】B[解析] AB 是⊙O 的直径，弦CD ⊥AB 于点E ，由垂径定理可以得到CE ＝DE ，BC ︵＝BD ︵，AC ︵＝AD ︵.但并不一定能得到OE ＝BE ，OC ＝BC ，从而A ，C ，D 选项都是错误的． 故选B.3. 【答案】A[解析] ∵BC ︵＝CD ︵＝DE ︵，∠COD ＝34°，∴∠BOC ＝∠COD ＝∠EOD ＝34°，∴∠AOE ＝180°－∠EOD －∠COD －∠BOC ＝78°. 又∵OA ＝OE ，∴∠AEO ＝∠OAE ，∴∠AEO ＝12×(180°－78°)＝51°.4. 【答案】C5. 【答案】A[解析] 把∠AOB 三等分，得到的每一份角所对的弧都等于CD ︵，因此有AB ︵＝3CD ︵.6. 【答案】D[解析] 如图，过点O 作OD ⊥AB 于点D ，连接OA .根据题意，得OD ＝12OA ＝1.再根据勾股定理，得AD ＝ 3.根据垂径定理，得AB ＝2 3.7. 【答案】B[解析] 连接OC ，则OC ＝4，OE ＝3.在Rt △OCE 中，CE ＝OC2－OE2＝42－32＝7.因为AB ⊥CD ，所以CD ＝2CE ＝2 7.8. 【答案】C9. 【答案】B10. 【答案】D[解析] 如图，连接OB ，OA ，OP ，设OB 与AP 交于点D.由PB＝AB 可知PB ︵＝AB ︵，从而可知OB ⊥AP.运用“一条弧所对的圆周角等于它所对的圆心角的一半”及“同圆的半径相等”可知△OAB 为等边三角形，在Rt △OAD 中，运用“在直角三角形中，30°角所对的直角边等于斜边的一半”及勾股定理列方程可求得AD 的长，从而可求出AP 的长为5 3.故选D.二、填空题（本大题共8道小题）11. 【答案】2或14 [解析] ①当弦AB 和CD 在圆心同侧时，连接OA ，OC ，过点O 作OE ⊥CD 于点F ，交AB 于点E ，如图①， ∵AB ＝16 cm ，CD ＝12 cm ， ∴AE ＝8 cm ，CF ＝6 cm. ∵OA ＝OC ＝10 cm ， ∴EO ＝6 cm ，OF ＝8 cm ， ∴EF ＝OF －OE ＝2 cm ；②当弦AB 和CD 在圆心异侧时，连接OA ，OC ，过点O 作OE ⊥CD 于点E 并反向延长交AB 于点F ，如图②，∵AB ＝16 cm ，CD ＝12 cm ， ∴AF ＝8 cm ，CE ＝6 cm. ∵OA ＝OC ＝10 cm ， ∴OF ＝6 cm ，OE ＝8 cm ， ∴EF ＝OF ＋OE ＝14 cm.∴AB 与CD 之间的距离为2 cm 或14 cm.12. 【答案】30°[解析] 如图，连接OC .∵AB 是⊙O 的直径，AC ︵＝CD ︵＝BD ︵，∴∠AOC ＝∠COD ＝∠DOB ＝60°.∵OA ＝OC ，∴△AOC 是等边三角形， ∴∠A ＝60°.∵CE ⊥OA ，∴∠AEC ＝90°， ∴∠ACE ＝90°－60°＝30°.13. 【答案】6 90 [解析] ∵AB 为⊙M 的直径，∴AB ＝4.当点O 到AB 的距离最大时，△AOB 的面积最大，此时AB ⊥x 轴于点M ， ∴△AOB 的面积的最大值为12×4×3＝6，∠AMO ＝90°. 即此时A ，B 两点所在直线与x 轴的夹角等于90°.14. 【答案】50[解析] 连接OA ，则OA ＝OB ，OA ＝OC ，∴∠OAB ＝∠B ，∠OAC ＝∠C ，∴∠BAC ＝∠OAB ＋∠OAC ＝∠B ＋∠C ＝20°＋30°＝50°.15. 【答案】65[解析] ∵∠C ＝25°，∴∠A ＝∠C ＝25°.∵⊙O 的直径AB 过弦CD 的中点E ， ∴AB ⊥CD ，∴∠AED ＝90°， ∴∠D ＝90°－25°＝65°.16. 【答案】3 [解析] 如图，连接OD ，过点O 作OH ⊥AB 于点H ，则AH ＝BH＝12AB ＝ 3.∵CD ⊥OC ，∴CD ＝OD 2－OC 2.∵OD 为⊙O 的半径，∴当OC 最小时，CD 最大．当点C 运动到点H 时，OC 最小，此时CD ＝BH ＝3，即CD 的最大值为 3.17. 【答案】40[解析] ∵∠BCD ＝180°－∠A ＝125°，∠CBF ＝∠A ＋∠E ＝85°，∴∠F ＝∠BCD －∠CBF ＝125°－85°＝40°.18. 【答案】(902n －1)[解析] 当n ＝1时，∠A 1OB 1＝90°；当n ＝2时，∠A 2OB 2＝90°2＝45……所以∠A n OB n ＝(902n －1)°.三、解答题（本大题共4道小题）19. 【答案】解：(1)证明：如图，连接DE. ∵BD 是⊙O 的直径， ∴∠DEB ＝90°，即DE ⊥AB. 又∵E 是AB 的中点， ∴AD ＝BD ，∴∠1＝∠B. 又∵∠B ＝∠F ，∴∠1＝∠F.(2)∵∠1＝∠F ，∴AE ＝EF ＝2 5， ∴AB ＝2AE ＝4 5.在Rt △ABC 中，∵AC ＝4，∠C ＝90°， ∴BC ＝AB2－AC2＝8. 设CD ＝x ，则AD ＝BD ＝8－x. 在Rt △ACD 中，∵∠C ＝90°，∴AC2＋CD2＝AD2，即42＋x2＝(8－x)2， 解得x ＝3，即CD ＝3.20. 【答案】证明：如图，取AB 的中点O ，连接OC ，OD.∵△ABC 和△ABD 都是直角三角形，且∠ACB ＝∠ADB ＝90°，∴OC ，OD 分别为Rt △ABC 和Rt △ABD 斜边上的中线，∴OC ＝OA ＝OB ，OD ＝OA ＝OB ，∴OA ＝OB ＝OC ＝OD ，∴A ，B ，C ，D 四点在同一个圆上．21. 【答案】(1)连接OA OC 、，过O 作OH AC ⊥于点H ，如图1，∵120ABC ∠=︒，∴18060AMC ABC ∠=-∠=︒︒，∴2120AOC AMC ∠=∠=︒，∴1602AOH AOC ∠=∠=︒， ∵132AH AC ==， ∴2sin60AH OA ==︒， 故⊙O 的半径为2．(2)在BM 上截取BE BC =，连接CE ，如图2，∵120ABC ∠=︒，BM 平分ABC ∠，∴60ABM CBM ∠=∠=︒，∵60MBC BE BC ︒∠==，，∴EBC △是等边三角形，∴60CE CB BE BCE ==∠=︒，， ∴60BCD DCE ∠+∠=︒，∵60ACM ∠=︒，∴60ECM DCE ∠+∠=︒，∴ECM BCD ∠=∠，∴6060CAM CBM ACM ABM ∠︒=∠︒=∠=∠=，， ∴ACM △是等边三角形，∴AC CM =，∴ACB MCE △≌△，∴AB ME =，∵ME EB BM +=，∴AB BC BM +=．22. 【答案】⎝ ⎛⎭⎪⎫360n m 解：P 为半圆ADB ︵的中点． 证明：如图，连接OP .∵∠OCD 的平分线交⊙O 于点P ，∴∠PCD ＝∠PCO .∵OC ＝OP ，∴∠PCO ＝∠OPC ，∴∠PCD ＝∠OPC ，∴OP ∥CD .∵CD ⊥AB ，∴OP ⊥AB ，∴AP ︵＝BP ︵，即P 为半圆ADB ︵的中点．24.2.2直线和圆的位置关系一．选择题1．如图，AB 、AC 是⊙O 的切线，B 、C 为切点，∠A ＝50°，点P 是圆上异于B 、C ，则∠BPC 的度数是（ ）A．65°B．115°C．115°或65°D．130°或65°2．△ABC中，AB＝13，BC＝5，点O是AC上的一点，⊙O与BC相切于点C，与AB相切于点D，则⊙O的半径为（）A．B．3C．D．53．如图，AB为⊙O的切线，A为切点，BO交⊙O于点C，点D在⊙O上，若∠ABO的度数是32°，则∠ADC的度数是（）A．15°B．16°C．29°D．58°4．如图，△ABC中，∠A＝80°，点O是△ABC的内心，则∠BOC的度数为（）A．100°B．160°C．80°D．130°5．如图，在△ABC中，以AB为直径的圆交AC于点D，⊙O的切线DE交BC于点E，若∠A＝35°，则∠CDE是（）A．35°B．45°C．55°D．65°6．如图，射线BM与⊙O相切于点B，若∠MBA＝140°，则∠ACB的度数为（）A．40°B．50°C．60°D．707．如图，P A、PB是⊙O切线，A、B为切点，AC是直径，∠P＝40°，则∠BAC＝（）A．40°B．80°C．20°D．10°8．如图，AB是⊙O的直径，BP是⊙O的切线，AP与⊙O交于点C，D为BC上一点，若∠P＝36°，则∠ADC等于（）A．18°B．27°C．36°D．54°9．如图，已知P A，PB是⊙O的两条切线，A，B为切点，线段OP交⊙O于点M．给出下列四种说法：①P A＝PB；②OP⊥AB；③四边形OAPB有外接圆；④M是△AOP外接圆的圆心．其中正确说法的个数是（）A．1B．2C．3D．410．如图，AB为⊙O的切线，切点为A，OB交⊙O于点C，点D在⊙O上，且OD∥AC，若∠B＝38°，则∠ODC的度数为（）A．46°B．48°C．52°D．58°二．填空题11．如图，已知圆O为Rt△ABC的内切圆，切点分别为D、E、F，且∠C＝90°，AB＝13，BC＝12，则圆O的半径为．12．如图，AB是⊙O的弦，点C在过点B的切线上，且OC⊥OA，OC交AB于点P，已知∠OAB＝23°，则∠OCB＝°．13．已知点P是圆外一点，过点P引圆的两条切线P A、PB，切点分别为A、B，点C是圆上异于A、B的点，若∠P＝70°，则∠ACB＝．14．如图，AB，AC，BD是⊙O的切线，P，C，D为切点，若AB＝5，AC＝4，则BD的长为．15．如图，等腰△ABC的内切圆⊙O与AB，BC，CA分别相切于点D，E，F，且AB＝AC＝5，BC＝6，则DE的长是．三．解答题16．已知：如图，Rt△ABC中，∠ACB＝90°，以AC为弦作⊙O，交BC的延长线于点D，且DC＝BC，过点D作⊙O的切线，交AB的延长线于点E．（1）猜想∠CAB与∠BDE的数量关系，并说明理由；（2）若AB＝BE，则∠E的度数为°．17．如图，在等腰三角形ABD中，AB＝AD，点C为BD上一点，以BC为直径作⊙O，且点A恰好在⊙O上，连接AC．（1）若AC＝CD，求证：AD是⊙O的切线．（2）在（1）的条件下，若CD＝1，求⊙O的直径．18．如图，△ABC内接于⊙O，∠B＝60°，CD是⊙O的直径，点P是CD延长线上的一点且AP＝AC．（1）求证：P A是⊙O的切线；（2）若AB＝2+，BC＝4，求⊙O的半径．参考答案1．解：∵AB、AC是⊙O的切线，∴OB⊥AB，OC⊥AC，∵∠A＝50°，∴∠BOC＝180°﹣50°＝130°，当点P在优弧BC上时，∠BPC＝∠BOC＝65°，当点P′在劣弧BC上时，∠BP′C＝180°﹣65°＝115°，故选：C．2．解：依题意画出图形，连接OD，如图：∵⊙O与BC相切于点C，与AB相切于点D，∴∠ACB＝90°，∠ADO＝90°，∴∠ACB＝∠ADO，又∵∠A＝∠A，∴△ADO∽△ACB，∴＝，在△ABC中，AB＝13，BC＝5，由勾股定理得：AC＝＝12，设⊙O的半径为r，则有：＝，解得：r＝．故选：C．3．解：∵AB为⊙O的切线，∴∠OAB＝90°，∴∠AOB＝90°﹣∠ABO＝58°，由圆周角定理得，∠ADC＝∠AOB＝29°，故选：C．4．解：∵∠A＝80°，∴∠ABC+∠ACB＝180°﹣∠A＝100°，∵点O是△ABC的内心，∴∠OBC+∠OCB＝（∠ABC+∠ACB）＝50°，∴∠BOC＝180°﹣50°＝130°．故选：D．5．解：连接DB，OD，∵AB是⊙O的直径，∴∠ADB＝90°，∵OA＝OD，∠A＝35°，∴∠ODA＝∠A＝35°，∴∠ODB＝90°﹣35°＝55°，∵DE是⊙O的切线，OD是⊙O的半径，∴∠ODE＝90°，∴∠BDE＝∠ODE﹣∠ODB＝90°﹣55°＝35°，∴∠CDE＝∠CDB﹣∠BDE＝90°﹣35°＝55°，故选：C．6．解：∵射线BM与⊙O相切于点B，∴BC⊥BM，∴∠MBC＝90°，∴∠ABC＝∠MBA﹣∠MBC＝140°﹣90°＝50°，∵BC为直径，∴∠BAC＝90°，∴∠ACB＝90°﹣50°＝40°．故选：A．7．解：连接OB，∵P A、PB是⊙O切线，A、B为切点，∴∠OAP＝∠OBP＝90°，∵∠P＝40°，∴∠AOB＝360°﹣∠OAP﹣∠P﹣∠OBP＝140°，∵OA＝OB，∴∠BAC＝∠OBA＝（180°﹣∠AOB）＝20°，故选：C．8．解：连接BC，∵BP是⊙O的切线，∴AB⊥BP，∴∠ABP＝90°，∴∠BAP＝90°﹣∠P＝54°，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠ABC＝90°﹣∠BAP＝36°，由圆周角定理得，∠ADC＝∠ABC＝36°，故选：C．9．解：∵P A，PB是⊙O的两条切线，A，B为切点，∴P A＝PB，所以①正确；∵OA＝OB，P A＝PB，∴OP垂直平分AB，所以②正确；∵P A，PB是⊙O的两条切线，A，B为切点，∴OA⊥P A，OB⊥PB，∴∠OAP＝∠OBP＝90°，∴点A、B在以OP为直径的圆上，∴四边形OAPB有外接圆，所以③正确；∵只有当∠APO＝30°时，OP＝2OA，此时PM＝OM，∴M不一定为△AOP外接圆的圆心，所以④错误．故选：C．10．解：连接OA，∵AB为⊙O的切线，∴OA⊥AB，∴∠OAB＝90°，∴∠AOB＝90°﹣∠B＝52°，∵OA＝OC，∴∠OCA＝∠OAC＝×（180°﹣52°）＝64°，∵OD∥AC，∴∠DOC＝∠OCA＝64°，∵OC＝OD，∴∠ODC＝∠OCD＝×（180°﹣64°）＝58°，故选：D．11．解：在Rt△ABC中，∵∠C＝90°，AB＝13，BC＝12，∴AC＝＝5，∵⊙O为Rt△ABC的内切圆，切点分别为D，E，F，∴BD＝BF，AD＝AE，CF＝CE，如图，连接OE，OF，∵OE⊥AC，OF⊥BC，OE＝OF，∴∠OEC＝∠C＝∠OFC＝90°，∴四边形OECF是正方形，设OE＝OF＝CE＝CF＝x，则AD＝AE＝5﹣x，BF＝BD＝12﹣x，∵AD+BD＝13，∴5﹣x+12﹣x＝13，∴x＝2，则圆O的半径为2．故答案为：2．12．解：连接OB，∵BC是⊙O的切线，∴OB⊥BC，∴∠OBA+∠CBP＝90°，∵OC⊥OA，∴∠A+∠APO＝90°，∵OA＝OB，∠OAB＝23°，∴∠OAB＝∠OBA＝23°，∴∠APO＝∠CBP＝67°，∵∠APO＝∠CPB，∴∠CPB＝∠APO＝67°，∴∠OCB＝180°﹣67°﹣67°＝46°，故答案为：46．13．解：①当C和P在O的异侧时，如图1，连接OA，OB，∵P A，PB是⊙O的切线，∴OA⊥P A，OB⊥PB，∴∠P AO＝∠PBO＝90°，∴∠AOB＝360°﹣∠P AO﹣∠PBO﹣∠P＝360°﹣90°﹣90°﹣70°＝110°，∴∠ACB＝∠AOB＝55°；②当C和P在O的同侧时，如图2，连接OA，OB，由①知∠AOB＝110°，∵∠ACB+∠AOB＝180°，∴∠ACB＝180°﹣∠AOB＝125°；综上所述：∠ACB＝55°或125°，故答案为：55°或125°．14．解：∵AC，AP为⊙O的切线，∴AC＝AP＝4，∵BP，BD为⊙O的切线，∴BP＝BD，∴BD＝BP＝AB﹣AP＝5﹣4＝1．故答案为：1．15．解：连接OA、OE、OB，OB交DE于H，如图，∵等腰△ABC的内切圆⊙O与AB，BC，CA分别相切于点D，E，F，∴OA平分∠BAC，OE⊥BC，OD⊥AB，BE＝BD，∵AB＝AC，∴AO⊥BC，∴点A、O、E共线，即AE⊥BC，∴BE＝CE＝3，在Rt△ABE中，AE＝＝4，∵BD＝BE＝3，∴AD＝2，设⊙O的半径为r，则OD＝OE＝r，AO＝4﹣r，在Rt△AOD中，r2+22＝（4﹣r）2，解得r＝，在Rt△BOE中，OB＝＝，∵BE＝BD，OE＝OD，∴OB垂直平分DE，∴DH＝EH，OB⊥DE，∵HE•OB＝OE•BE，∴HE＝＝＝，∴DE＝2EH＝．故答案为：．16．解：（1）∠CAB＝∠BDE．理由如下：连接AD，如图，∵∠ACB＝90°，∴∠ACD＝90°，∴AD为⊙O的直径，∵DE为切线，∴AD⊥DE，∴∠ADC+∠BDE＝90°，∵DC＝BC，AC⊥BD，∴AD＝AB，∴∠ADC＝∠ABC，∵∠BAC+∠ABC＝90°，∴∠BAC＝∠BDE；（2）∵∠ADE＝90°，AB＝BE，∴BD＝AB＝BE，而AD＝AB，∴△ABD为等边三角形，∴∠BAD＝60°，∴∠E＝90°﹣60°＝30°．故答案为30．17．解：（1）如图，连接OA．∵OA＝OB，∴∠B＝∠OAB，∵AB＝AD，∴∠B＝∠D，∵AC＝CD，∴∠D＝∠CAD，∴∠OAB＝∠CAD，∵BC为直径，∴∠BAC＝90°，∴∠OAD＝90°，即OA⊥AD，∵OA是⊙O的半径，∴AD是⊙O的切线；（2）设⊙O的半径为x，则OA＝OC＝x，BC＝2x，∵∠B＝∠D，AB＝AD，∠BAC＝∠OAD＝90°，∴△BAC≌△DAO，∴BC＝DO，∵CD＝1，∴DO＝OC+CD＝x+1，∴2x＝x+1，∴x＝1，即⊙O的直径为2．18．（1）证明：连接OA，∵∠B＝60°，∴∠AOC＝2∠B＝120°，又∵OA＝OC，∴∠OAC＝∠OCA＝30°，又∵AP＝AC，∴∠P＝∠ACP＝30°，∴∠OAP＝∠AOC﹣∠P＝90°，∴OA⊥P A，∴P A是⊙O的切线；（2）解：过点C作CE⊥AB于点E．在Rt△BCE中，∠B＝60°，BC＝4，∴BE＝BC＝2，CE＝2，∵AB＝2+，∴AE＝AB﹣BE＝，在Rt△ACE中，AC＝＝3，∴AP＝AC＝3．在Rt△P AO中，OA＝OP＝3，∴⊙O的半径为3．24.3正多边形和圆一．选择题1．下列说法错误的是（）A．平分弦的直径垂直于弦B．圆内接四边形的对角互补C．任意三角形都有一个外接圆D．正n边形的中心角等于2．下列说法中正确的是（）A．直角三角形只有一条高B．三角形任意两个内角的和大于第3个内角C．在同圆中任意两条直径都互相平分D．如果一个多边形的各边都相等，那么它是正多边形3．如图，A、B、C是⊙O上顺次3点，若AC、AB、BC分别是⊙O内接正三角形、正方形、正n边形的一边，则n＝（）A．9B．10C．12D．154．如图，在正五边形ABCDE中，连结AC，以点A为圆心，AB为半径画圆弧交AC于点F，连接DF．则∠FDC的度数是（）A．18°B．30°C．36°D．40°5．下列说法中，正确的个数为（）①三角形的外角等于两个内角的和；②有两边和一角分别相等的两个三角形全等；③各边都相等的多边形是正多边形；④到角两边距离相等的点，在这个角的平分线上．A．1B．2C．3D．06．如图，正六边形ABCDEF内接于⊙O，点P是上的任意一点，则∠APB的大小是（）A．15°B．30°C．45°D．60°7．如图，四边形ABCD是⊙O的内接正方形，点P是上不同于点C的任意一点，则∠BPC的大小是（）A．22.5°B．45°C．30°D．50°8．如图，⊙O的周长等于4πcm，则它的内接正六边形ABCDEF的面积是（）A．B．C．D．9．如图，AC是⊙O的内接正四边形的一边，点B在弧AC上，且BC是⊙O的内接正六边形的一边．若AB是⊙O的内接正n边形的一边，则n的值为（）A．6B．8C．10D．1210．已知⊙O是正六边形ABCDEF的外接圆，P为⊙O上除C、D外任意一点，则∠CPD 的度数为（）A．30°B．30°或150°C．60°D．60°或120°二．填空题11．如图，将边长相等的正六边形和正五边形拼接在一起，则∠ABC的度数为°．12．已知正方形的半径是4，那么这个正方形的边心距是．13．已知正三角形ABC的半径长为R，那么△ABC的周长是．（用含R的式子表示）14．如图，正五边形ABCDE内接于⊙O，点F为BC上一点，连接AF，若∠AFC＝126°，则∠BAF的度数为．15．如图，△PQR是⊙O的内接正三角形，四边形ABCD是⊙O的内接正方形，BC∥QR，则∠BOQ＝．三．解答题16．如图，已知点O是正六边形ABCDEF的对称中心，G，H分别是AF，BC上的点，且AG＝BH．（1）求∠F AB的度数；（2）求证：OG＝OH．17．如图，⊙O的半径等于4cm，正六边形ABCDEF内接于⊙O（1）求圆心O到AF的距离；（2）求正六边形ABCDEF的面积．参考答案1．解：A、∵平分弦（不是直径）的直径垂直于弦，∴选项A符合题意；B、∵圆内接四边形的对角互补，∴选项B不符合题意；C、∵任意三角形都有一个外接圆，∴选项C不符合题意；D、∵正n边形的中心角等于，∴选项D不符合题意；故选：A．2．解：A、直角三角形有3条高，故原命题错误，不符合题意；B、钝角三角形的两个较小的锐角的和小于最大的钝角，故原命题错误，不符合题意；C、在同圆中任意两条直径都互相平分，正确，符合题意；D、如果一个多边形的各角相等，各边都相等，那么它是正多边形，故原命题错误，不符合题意；故选：C．3．解：如图，连接OA，OC，OB．∵若AC、AB分别是⊙O内接正三角形、正方形的一边，∴∠AOC＝120°，∠AOB＝90°，∴∠BOC＝∠AOC﹣∠AOB＝30°，由题意30°＝，∴n＝12，故选：C．4．解：∵五边形ABCDE是正五边形，∴∠AED＝∠EAB＝∠ABC＝108°，∵BA＝BC，∴∠BAC＝∠BCA＝36°，∴∠EAC＝72°，∴∠AED+∠EAC＝180°，∴DE∥AF，∵AE＝AF＝DE，∴四边形AEDF是菱形，∴∠EDF＝∠EAF＝72°，∵∠EDC＝108°，∴∠FDC＝36°，故选：C．5．解：①三角形的外角等于两个内角的和，错误，应该是三角形的外角等于和它不相邻两个内角的和．②有两边和一角分别相等的两个三角形全等，错误，应该是有两边和夹角分别相等的两个三角形全等．③各边都相等的多边形是正多边形，错误．缺少各个角相等这个条件．④到角两边距离相等的点，在这个角的平分线上．错误，这个点必须在这个角的内部．故选：D．6．解：连接OA、OB、如图所示：∵∠AOB＝＝60°，∴∠APC＝∠AOC＝30°，故选：B．7．解：如图，连接OB、OC，则∠BOC＝90°，根据圆周角定理，得：∠BPC＝∠BOC＝45°．故选：B．8．解：如图，连接OA、OB，作OG⊥AB于点G，∵⊙O的周长等于4πcm，∴⊙O的半径为：＝2，∵ABCDEF是⊙O的内接正六边形，∴OA＝OB＝AB＝2，∵OG⊥AB，∴AG＝BG＝AB＝1，∴OG＝，∴S△AOB＝AB•OG＝2×＝．∴它的内接正六边形ABCDEF的面积是6S△AOB＝6（cm2）．故选：C．9．解：连接AO、BO、CO，∵AC是⊙O内接正四边形的一边，∴∠AOC＝360°÷6＝90°，∵BC是⊙O内接正六边形的一边，∴∠BOC＝360°÷6＝60°，∴∠AOB＝∠AOC﹣∠BOC＝90°﹣60°＝30°，∴n＝360°÷30°＝12；故选：D．10．解：连接OC、OD，如图，∵⊙O是正六边形ABCDEF的外接圆，∴∠COD＝60°，当P点在弧CAD上时，∠CPD＝∠COD＝30°，当P点在弧CD上时，∠CPD＝180°﹣30°＝150°，综上所述，∠CPD的度数为30°或150°．故选：B．11．解：由题意得：正六边形的每个内角都等于120°，正五边形的每个内角都等于108°，∴∠ABC＝360°﹣120°﹣108°＝132°，故答案为：132．12．解：如图，根据正方形的性质知：△BOC是等腰直角三角形，过O作OE⊥BC于E，∵正方形的半径是4，∴BO＝4，∴OE＝BE＝BO＝2，故答案为：2．13．解：如图所示：连接OA、OB、OC，过O作OD⊥BC于D，∵△ABC是半径为R的等边三角形，∴OA＝OB＝OC＝R，∠ABC＝60°，∴∠OBD＝30°，∵OD⊥BC，∴∠ODB＝90°，OD＝OB＝R，∴BD＝OD＝R，∴BC＝2BD＝R，∴该三角形的周长为3R，故答案为：3R．14．解：∵正五边形ABCDE内接于⊙O，∴∠ABC＝＝108°，∵∠AFC＝126°，∴∠BAF＝∠AFC﹣∠ABF＝126°﹣108°＝18°．故答案为18°．15．解：连结OA，OD，∵△PQR是⊙O的内接正三角形，∴PQ＝PR＝QR，∴∠POQ＝×360°＝120°，∵BC∥QR，OP⊥QR，∵BC∥QR，∴OP⊥BC，∵四边形ABCD是⊙O的内接正方形，∴OP⊥AD，∠AOD＝90°，∴＝，∴∠AOP＝∠DOP，∴∠AOP＝×90°＝45°，∴∠AOQ＝∠POQ﹣∠AOP＝75°．∵∠AOB＝90°，∴∠QOB＝15°，故答案为：15°．16．（1）解：∵六边形ABCDEF是正六边形，∴∠F AB＝＝120°；（2）证明：连接OA、OB，∵OA＝OB，∴∠OAB＝∠OBA，∵∠F AB＝∠CBA，∴∠OAG＝∠OBH，在△AOG和△BOH中，，∴△AOG≌△BOH（SAS）∴OG＝OH．17．解：（1）过O作OH⊥AF于H，连接OA，OF，∵在正六边形ABCDEF中，∠BAF＝120°，∴∠OAF＝60°，∵OA＝4，∴AH＝OA＝2，∴OH＝＝＝2；∴圆心O到AF的距离为2；（2）∵OA＝OF，∠OAF＝60°，∴△OAF是等边三角形，∴AF＝OA＝4，∴S△AOF＝×4×2＝4，∴正六边形ABCDEF的面积＝6S△AOF＝24．24.4 弧长和扇形面积一、选择题1. 如图，AB，CD是⊙O的两条互相垂直的直径，O1，O2，O3，O4分别是OA，OB，OC，OD的中点．若⊙O的半径是2，则阴影部分的面积为()A．8 B．4C．4π＋4 D．4π－42. 如图，用一张半径为24 cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计)．如果圆锥形帽子的底面圆半径为10 cm，那么这张扇形纸板的面积是()A．240π cm2B．480π cm2C．1200π cm2D．2400π cm23. 一个圆锥的侧面积是底面积的2倍，则该圆锥侧面展开图的圆心角的度数是( )A ．120°B ．180°C ．240°D ．300°4. 如图，在边长为4的正方形ABCD 中，以点B 为圆心，AB 长为半径画弧，交对角线BD 于点E ，则图中阴影部分的面积是(结果保留π)( )A ．8－πB ．16－2πC ．8－2πD ．8－12π5. 如图AB 为半圆O 的直径，AB ＝4，C ，D 为AB ︵上两点，且AC ︵＝15BD ︵.若∠CED ＝52∠COD ，则BD ︵的长为( )图A.59πB.78πC.89πD.109π6. 如图，线段AB 经过⊙O 的圆心，AC ，BD 分别与⊙O 相切于点C ，D .若AC ＝BD ＝4，∠A ＝45°，则CD ︵的长度为( )A ．πB ．2πC ．2 2πD ．4π7. 如图0，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，∠CDB ＝30°，CD ＝2 3，则图中阴影部分的面积为( )A ．4πB ．2πC ．π D.2π38. 如图，△ABC 是等腰直角三角形，且∠ACB ＝90°.曲线CDEF…叫做“等腰直角三角形的渐开线”，其中CD ︵，DE ︵，EF ︵，…的圆心依次按A ，B ，C ，…循环．如果AC ＝1，那么曲线CDEF 和线段CF 围成图的面积为( )图A .（12＋72）4πB .（9＋52）4πC .（12＋72）π＋24D .（9＋52）π＋249. 如图，点I 为△ABC 的内心，AB ＝4，AC ＝3，BC ＝2，将∠ACB 平移使其顶点与点I 重合，则图中阴影部分的周长为( )A ．4.5B ．4C ．3D ．210. 如图所示，矩形纸片ABCD 中，AD ＝6 cm ，把它分割成正方形纸片ABFE 和矩形纸片EFCD 后，分别裁出扇形BAF 和半径最大的圆，恰好能作为一个圆锥的侧面和底面，则AB 的长为( )A．3.5 cm B．4 cm C．4.5 cm D．5 cm二、填空题11. 用一个圆心角为120°，半径为6的扇形作一个圆锥的侧面，则这个圆锥的底面圆的面积为________．12. 如图所示，有一直径是2米的圆形铁皮，现从中剪出一个圆心角是90°的最大扇形ABC，则：(1)AB的长为________米；(2)用该扇形铁皮围成一个圆锥，所得圆锥的底面圆的半径为________米．13. 如图，AB是⊙O的直径，AC是弦，AC＝3，∠BOC＝2∠AOC.若用扇形OAC(图中阴影部分)围成一个圆锥的侧面，则这个圆锥底面圆的半径是________．AB=，将半圆绕点A顺时针旋转14. (2019•十堰)如图，AB为半圆的直径，且660︒，点B旋转到点C的位置，则图中阴影部分的面积为__________．15. 如图，∠AOB＝90°，∠B＝30°，以点O为圆心，OA长为半径作弧交AB于点A，C，交OB于点D.若OA＝3，则阴影部分的面积为________．三、解答题16. 已知扇形的圆心角为120°，面积为300π cm2.(1)求扇形的弧长；(2)若把此扇形卷成一个圆锥，则这个圆锥的体积是多少？17. 已知一个圆锥的轴截面△ABC(如图0)是等边三角形，它的表面积为75π cm2，求这个圆锥的底面圆的半径和母线长．18. 当汽车在雨天行驶时，司机为了看清楚道路，要启动前方挡风玻璃上的雨刷．如图是某汽车的一个雨刷的转动示意图，雨刷杆AB与雨刷CD在B处固定连接(不能转动)，当杆AB绕点A转动90°时，雨刷CD扫过的面积是图中阴影部分的面积，现量得CD＝90 cm，∠DBA＝20°，AC＝115 cm，DA＝35 cm，试从以上信息中选择所需要的数据，求出雨刷扫过的面积．19. 如图是两个半圆，点O 为大半圆的圆心，AB 是大半圆的弦且与小半圆相切，AB ＝24，求图中阴影部分的面积．20. 如图①，在等腰三角形ABC 中，∠BAC ＝120°，AD 平分∠BAC ，且AD ＝6，以点A 为圆心，AD 长为半径画弧EF ，交AB 于点E ，交AC 于点F.(1)求由EF ︵及线段FC ，CB ，BE 围成的图形(图中阴影部分)的面积；(2)将阴影部分剪掉，余下扇形AEF ，将扇形AEF 围成一个圆锥的侧面，AE 与AF 正好重合，圆锥侧面无重叠(如图②)，求这个圆锥的高h.人教版 九年级数学 24.4 弧长和扇形面积 针对训练 -答案一、选择题1. 【答案】A2. 【答案】A[解析] ∵扇形的弧长l＝2·π·10＝20π(cm)，∴扇形的面积S＝12lR＝12×20π×24＝240π(cm2)．3. 【答案】B[解析] 设母线长为R，底面圆的半径为r，则底面圆的周长＝2πr，底面积＝πr2，侧面积＝πrR.∵侧面积是底面积的2倍，∴2πr2＝πrR，∴R＝2r.设该圆锥侧面展开图的圆心角为n°，则nπR180＝2πr，∴nπR180＝πR，∴n＝180.故选B.4. 【答案】C[解析] 在边长为4的正方形ABCD中，BD是对角线，∴AD＝AB＝4，∠BAD＝90°，∠ABE＝45°，∴S△ABD＝12AD·AB＝8，S扇形BAE＝45·π·42360＝2π，∴S阴影＝S△ABD－S扇形BAE＝8－2π.故选C.5. 【答案】D6. 【答案】B7. 【答案】D[解析] 如图，连接OD.∵CD⊥AB，∴CE＝DE＝3，∠CEO＝∠DEO＝90°.又∵OE＝OE，∴△COE≌△DOE，故S△COE＝S△DOE，即可得阴影部分的面积等于扇形OBD的面积．∵∠CDB＝30°，∴∠COB＝60°，∴∠OCD ＝30°，∴OE ＝12OC.在Rt △COE 中，CE ＝3，由勾股定理可得OC ＝2，∴OD ＝2.∵△COE ≌△DOE ，∴∠DOE ＝∠COE ＝60°，∴S 扇形OBD ＝60π·22360＝23π，即阴影部分的面积为2π3.故选D.8. 【答案】C [解析] 曲线CDEF 和线段CF 围成的图是由三个圆心不同，半径不同的扇形以及△ABC 组成的，所以根据面积公式可得 135π×1＋135π×（2＋1）2＋90π×（2＋2）2360＋12×1×1＝（12＋7 2）π＋24.9. 【答案】B [解析] 设CA ，CB 平移后分别交AB 于点M ，N ，连接AI ，BI.由平移可知AC ∥MI ，∴∠CAI ＝∠AIM.∵∠CAI ＝∠BAI ，∴∠BAI ＝∠AIM ，∴AM ＝MI.同理BN ＝NI.∴△MNI 的周长＝MI ＋NI ＋MN ＝AM ＋BN ＋MN ＝AB ＝4.故选B.10. 【答案】B [解析] AF ︵的长＝14·2π·AB ，右侧圆的周长为π·D E.∵裁出的扇形和圆恰好能作为一个圆锥的侧面和底面，∴14·2π·AB ＝π·DE ，∴AB ＝2DE ，即AE ＝2DE.∵AE ＋DE ＝AD ＝6，∴AB ＝4.故选B.二、填空题11. 【答案】4π [解析] 设此圆锥的底面圆的半径为r.由题意可得2πr ＝120π×6180，解得r ＝2，故这个圆锥的底面圆的半径为2，所以底面圆的面积为πr2＝4π.12. 【答案】(1)1 (2)14 [解析] (1)如图，连接BC.∵∠BAC ＝90°，∴BC 为⊙O 的直径，即BC ＝ 2.∵AB ＝AC ，AB2＋AC2＝BC2＝2，∴AB ＝1(米)．(2)设所得圆锥的底面圆的半径为r 米．根据题意，得2πr ＝90·π·1180，解得r ＝14.13. 【答案】12 [解析] 设这个圆锥底面圆的半径是r.∵∠BOC ＝2∠AOC ，∠BOC ＋∠AOC ＝180°，∴∠AOC ＝60°.又∵OA ＝OC ，∴△OAC 为等边三角形，∴OA ＝OC ＝AC ＝3，∴lAC ︵＝60π×3180＝2πr ，解得r ＝12，∴这个圆锥底面圆的半径是12.14. 【答案】6π【解析】由图可得， 图中阴影部分的面积为：22260π6π(62)π(62)6π36022⨯⨯⨯÷⨯÷+-=，故答案为：6π．15. 【答案】34π [解析] 如图，连接OC ，过点C 作CN ⊥AO 于点N ，CM ⊥OB于点M.∵∠AOB ＝90°，∠B ＝30°，∴∠A ＝60°.∵OA ＝OC ，∴△AOC 为等边三角形，∴∠AOC ＝60°，AC ＝OA.∵OA ＝3，∴AC ＝OA ＝3.∵CN ⊥OA ，∴AN ＝ON ＝12OA ＝32，∴CN ＝32 3，∴S △AOC ＝12OA·CN ＝94 3.∵∠AOB ＝90°，CN ⊥OA ，CM ⊥OB ，∴四边形CNOM 为矩形，∴CM ＝ON ＝32.在Rt △AOB 中，∠B ＝30°，OA ＝3，∴AB ＝2OA ＝6，∴OB ＝3 3，∴S △OCB ＝12OB·CM ＝94 3. ∵∠AOC ＝60°，OA ＝3，∴S 扇形OAC ＝60π·32360＝32π.∵∠COD ＝90°－60°＝30°，∴S 扇形OCD ＝30π·32360＝34π，∴S 阴影＝S 扇形OAC －S △AOC ＋S △OCB －S 扇形OCD ＝34π.三、解答题16. 【答案】解：(1)设扇形的半径为r cm.由题意，得120π×r2360＝300π，解得r ＝30，∴扇形的弧长＝120π×30180＝20π(cm)．(2)设圆锥的底面圆的半径为x cm ，则2π·x ＝20π，解得x ＝10， ∴圆锥的高＝302－102＝20 2(cm)，∴圆锥的体积＝13·π·102·20 2＝ 2000 23π(cm3)．17. 【答案】解：∵轴截面△ABC 是等边三角形，∴AC ＝BC ＝2OC.由题意，得π·OC·AC ＋π·OC 2＝75π，∴3π·OC2＝75π，∴OC2＝25.∵OC>0，∴OC ＝5 cm ，∴AC ＝2OC ＝2×5＝10(cm)．即这个圆锥的底面圆的半径为5 cm ，母线长为10 cm.18. 【答案】解：由题意可知△ACD ≌△AC′D′，所以可将△AC′D′旋转到△ACD 处，使阴影部分面积成为一部分环形面积，可通过两扇形面积之差求得，即雨刷CD 扫过的面积S 阴影＝S 扇形ACC′－S 扇形ADD′＝90π×1152360－90π×352360＝π4(115＋35)×(115－35)＝3000π(cm2)．答：雨刷扫过的面积为3000π cm2.19. 【答案】 [解析] 小圆向右平移，使它的圆心与大圆的圆心重合，于是阴影部分的面积可转化为大半圆的面积减去小半圆的面积．解：将小半圆向右平移，使两半圆的圆心重合，如图，连接OB ，过点O 作OC ⊥AB 于点C ，则AC ＝BC ＝12.∵AB 是大半圆的弦且与小半圆相切，∴OC 为小半圆的半径，∴S 阴影＝S 大半圆－S 小半圆＝12π·OB2－12π·OC2＝12π(OB2－OC2)＝12π·BC2＝72π.20. 【答案】解：(1)∵在等腰三角形ABC 中，∠BAC ＝120°，∴AB ＝AC ，∠B ＝∠C ＝30°.∵AD 平分∠BAC ，∴AD ⊥BC ，BD ＝CD.在Rt △ABD 中，由∠B ＝30°，AD ＝6，可得AB ＝12，BD ＝6 3，∴BC ＝2BD ＝12 3，∴由EF ︵及线段FC ，CB ，BE 围成的图形(图中阴影部分)的面积＝S △ABC －S 扇形AEF ＝12×6×12 3－120·π·62360＝36 3－12π. (2)设圆锥的底面圆的半径为r.根据题意，得2πr ＝120·π·6180，解得r ＝2，∴这个圆锥的高h ＝62－22＝4 2.。

2018-2019学年度人教版数学九年级上册同步练习24.2.1点和圆的位置关系.选择题（共16小题）1 •已知。

O 的半径为5,若OP=6,则点P 与。

O 的位置关系是（）A. 点P 在。

O 内B .点P 在。

O 外 C.点P 在。

O 上 D .无法判断2. 在平面直角坐标系中，圆心为坐标原点，。

O 的半径为5,则点P （- 3, 4） 与。

O 的位置关系是（ ） A. 点P 在。

O 外 B .点P 在。

O 上 C •点P 在。

O 内 D .无法确定3. 平面内有一点P 到圆上最远的距离是6,最近的距离是2,则圆的半径是（ ）A. 2 B . 4 C. 2 或 4 D . 84. 如图，在矩形ABCD 中，AB=4, AD=3,以顶点D 为圆心作半径为x 的圆，若 要求另外三个顶点A 、B C 中至少有一个点在圆内，且至少有一个点在圆外,5. 如图，AB 是半圆O 的直径，点D 在半圆O 上，AB=2_ 一，AD=10, C 是弧BD上的一个动点，连接 AC,过D 点作DH 丄AC 于H ,连接BH,在点C 移动的过 程中，BH 的最小值是（ ）A . 5B . 6 C. 7 D . 86. 如图，在平面直角坐标系中，。

A 的半径为1,圆心A 在函数y=x 的图象上运 动，下列各点不可能落入O A 的内部的是（ ）3< r v 5 C. 3< r <5 D . r >4 B .7. 下随有关圆的一些结论：①任意三点确定一个圆；②相等的圆心角所对的弧 相等；③平分弦的直径垂宜于弦；并且平分弦所对的弧，④圆内接四边形对角互补•其中错误的结论有（8. 下列有关圆的一些结论①任意三点可以确定一个圆；②相等的圆心角所对的 弧相等；③平分弦的直径垂直于弦，并且平分弦所对的弧；④圆内接四边形对角互补.其中正确的结论是（9. 如图，已知点平面直角坐标系内三点 O P 经过点A 、B C,则点P 的坐标为（） C.（ 4,亍） D .（ 4,）10•如图所示，△ ABC 内接于。

人教版九年级数学上册《24.2.1点和圆的位置关系》同步测试题带答案一、单选题1．已知O 的半径为4cm ，A 是线段OP 的中点 OP 8cm =，点A 与O 的位置关系是（ ） A ．在圆内B ．在圆上C ．在圆外D ．不能确定2．牛顿曾说过：“反证法是数学家最精良的武器之一．”那么我们用反证法证明：“在一个三角形中，至少有一个内角小于或等于60?︒时，第一步先假设（ ） A ．三角形中有一个内角小于60° B ．三角形中有一个内角大于60° C ．三角形中每个内角都大于60° D ．三角形中没有一个内角小于60°3．下列说法中正确的命题是（ ） A ．一个三角形只有一个外接圆 B ．平分弦的直径，平分这条弦所对的弧 C ．过三点可以画一个圆D ．三角形的外心到三角形的三边距离相等4．平面上有四个点，过其中任意3个点一共能确定圆的个数为（ ） A ．0或3或4B ．0或1或3C ．0或1或3或4D ．0或1或45．⊙O 的半径为5，点A 与圆心O 的距离为OA ＝4，则点A 与⊙O 的位置关系为( ) A ．点A 在⊙O 内 B ．点A 在⊙O 上C ．点A 在⊙O 外D ．以上三种情况都有可能6．有下列五个命题：⊙等弧所对的圆心角相等；⊙经过三个点一定可以作圆；⊙三角形的外心到三角形各顶点的距离都相等；⊙长度相等的两条弧是等弧；⊙直角三角形的外心是斜边的中点．其中正确的有（ ） A ．5个B ．4个C ．3个D ．2个二、填空题7．平面内有一点P 到圆上最远距离是8，最近距离是4，则圆的半径是8．在ABC 中6AB AC BC ==，，ABC 外接圆的半径为5，ABC 则的面积为 . 9．已知直角三角形的两条直角边长分别是3厘米，4厘米，则此直角三角形的重心与外心之间的距离为 厘米．10．如图所示，在平面直角坐标系xOy 中，点P 是钝角ABC 的外心，点A 、B 、P 的坐标分别为()1,0 ()2,5 ()4,2 若第一象限的点C 横坐标、纵坐标均为整数，则点C 的坐标为 ．11．在平面直角坐标系中，过三点A （0，0），B （2，2），C （4，0）的圆的圆心坐标为 . 12．如图，O 是ABC 的外接圆，M 、N 分别是AB 、AC 的中点，连接OM 、ON ，分别交BC 于点F 、E ，若5BF =，FE=3，EC=4，则ABC 的面积为 ．三、解答题13．如图，点A 、B 、C 三个点不在一条直线上．(1)那么经过A 、B 、C 三个点可以画个圆吗？如果能，请在图中画出来（要求尺规作图，保留作图痕迹）；如果不能，说明理由．(2)分别连接AB 、BC 、AC ，若ABC 是等边三角形，边长为6，求ABC 外接圆的半径．14．在直角坐标系中，以点()2,0A 为圆心作圆，使圆经过点()0,4B -，如图所示，试判断()0,4C ()2,0D - ()0,8E 与A 的位置关系.若点()0,M m 在A 外，求m 的取值范围.15．如图是一块残缺的圆轮片，点A 、B 、C 在圆弧E 上． （1）画出所在的⊙O ；（2）若AB=BC=60，⊙ABC=120°，求所在⊙O 的半径．16．某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下图是水平放置的破裂管道有水部分的截面．(1)请你补全这个输水管道的圆形截面；(2)若这个输水管道有水部分的水面宽16AB =cm ，水面最深地方的高度为4cm ，求这个圆形截面的半径；(3)在（2）的条件下，小明把一只宽12cm 的方形小木船放在修好后的圆柱形水管里，已知船高出水面13cm ，问此小船能顺利通过这个管道吗？ 17．按照下列要求作出图形(不写作法，保留作图痕迹)(1)尺规作图：将图1中的破轮子复原，已知弧上三点A，B，C．画出该轮的圆心；(2)如图2，矩形ABCD的顶点A在圆上，顶点B，C，D在圆内．请仅用无刻度的直尺画出图2中的圆心O．18．已知二次函数22y ax ax c=++的图象交x轴于A、B两点（其中A在B的左侧），交y 轴的正半轴于点C，且AB长为4．(1)请直接写出A、B两点的坐标；(2)设△ABC的外接圆的圆心为点M．⊙若点M到两坐标轴的距离相等，请求出这个二次函数的表达式；⊙若点M在△ABC的边上，设二次函数22=++的图象的顶点为D，连接DM，问：y ax ax c线段DM上是否存在这样的点P，使得直线OP将△ABC的面积分成相等两部分？若存在，请直接写出点P的坐标；若不存在，请说明理由．题号 1 2 3 4 5 6答案 B C A C B C1．B 2．C 3．A 4．C 5．B 6．C 7．2 8．27或3 9．5610．（1，4）或（6，5） 11．（2，0） 12．24 13．(1)能 (2)314．C 在A 上、D 在A 内、E 在A 外，4m >或4m <-15．（2）60.16．(2)这个圆形截面的半径为10cm (3)小船能顺利通过这个管道 18．(1)A (-3，0)，B (1，0)(2)⊙223y x x =--+或212133y x x =--+；⊙P (-123。

1《24.2.1 点和圆的位置关系》一、选择题1．下列说法正确的是（ ）A ．过一点A 的圆的圆心可以是平面上任意点B ．过两点A 、B 的圆的圆心在一条直线上C ．过三点A 、B 、C 的圆的圆心有且只有一点D ．过四点A 、B 、C 、D 的圆不存在2．若△ABC 的外接圆的圆心在△ABC 的内部，则△ABC 是（ ） A ．锐角三角形 B ．直角三角形 C ．钝角三角形 D ．无法确定3．在Rt △ABC 中，∠C=90°，AC=6cm ，BC=8cm ，则它的外心与顶点C 的距离为（ ） A ．5cm B ．6cm C ．7cm D ．8cm4．如图所示，一圆弧过方格的格点A 、B 、C ，试在方格中建立平面直角坐标系，使点A 的坐标为（﹣2，4），则该圆弧所在圆的圆心坐标是（ ）A ．（﹣1，2）B ．（1，﹣1）C ．（﹣1，1）D ．（2，1）5．Rt △ABC 中，∠C=90°，AC=2，BC=4，如果以点A 为圆心，AC 为半径作⊙A ，那么斜边中点D 与⊙A 的位置关系是（ ）A ．点D 在⊙A 外B ．点D 在⊙A 上C ．点D 在⊙A 内 D ．无法确定6．若⊙A 的半径为5，圆心A 的坐标是（3，4），点P 的坐标是（5，8），你认为点P 的位置为（ ） A ．在⊙A 内 B ．在⊙A 上 C ．在⊙A 外 D ．不能确定 7．如图，⊙O 是△ABC 的外接圆，若∠B=30°，AC=，则⊙O 的直径为（ ）2A ．1B ．C ．2D ．8．用反证法证明命题“三角形中必有一个内角小于或等于60°”时，首先应该假设这个三角形中（ ）A ．有一个内角小于60°B ．每一个内角都小于60°C ．有一个内角大于60°D ．每一个内角都大于60° 二、填空题9．点A 在以O 为圆心，3cm 为半径的⊙O 内，则点A 到圆心O 的距离d 的范围是______． 10．如图，在△ABC 中，∠ACB=90°，AC=2cm ，BC=4cm ，CM 为中线，以C 为圆心，cm 为半径作圆，则A 、B 、C 、M 四点在圆外的有______，在圆上的有______，在圆内的有______．11．若AB=4cm ，则过点A 、B 且半径为3cm 的圆有______个．12．在△ABC 中，BC=24cm ，外心O 到BC 的距离为6cm ，则△ABC 外接圆的半径为______． 13．一点和⊙O 上的最近点距离为4cm ，最远距离为9cm ，则这个圆的半径是______．14．阅读下面材料：对于平面图形A ，如果存在一个圆，使图形A 上的任意一点到圆心的距离都不大于这个圆的半径，则称图形A 被这个圆所覆盖．回答下列问题：（1）边长为1cm 的正方形被一个半径为r 的圆所覆盖，r 的最小值是______ cm ； （2）边长为1cm 的等边三角形被一个半径为r 的圆所覆盖，r 的最小值是______ cm ．15．若Rt △ABC 的两条直角边a ，b 是方程x 2﹣3x+1=0的两根，则Rt △ABC 的外接圆面积是______． 三、解答题16．已知圆的半径等于5cm ，根据下列点P 到圆心的距离：（1）4cm ；（2）5cm ；（3）6cm ，判定点P 与圆的位置关系，并说明理由．17．在Rt△ABC中，∠C=90°，BC=3m，AC=4m，以B为圆心，以BC为半径作⊙B，D、E是AB、AC中点，A、C、D、E分别与⊙O有怎样的位置关系？（画出图形，写过程）18．（教材变式题）如图所示，△ABC中，AB=AC=10，BC=12，求△ABC外接圆的半径．19．如图，AD为△ABC外接圆的直径，AD⊥BC，垂足为点F，∠ABC的平分线交AD于点E，连接BD，CD．（1）求证：BD=CD；（2）请判断B，E，C三点是否在以D为圆心，以DB为半径的圆上？并说明理由．20．某公园有一个边长为4米的正三角形花坛，三角形的顶点A、B、C上各有一棵古树．现决定把原来的花坛扩建成一个圆形或平行四边形花坛，要求三棵古树不能移动，且三棵古树位于圆周上或平行四边形的顶点上．以下设计过程中画图工具不限．（1）按圆形设计，利用图1画出你所设计的圆形花坛示意图；（2）按平行四边形设计，利用图2画出你所设计的平行四边形花坛示意图；（3）若想新建的花坛面积较大，选择以上哪一种方案合适？请说明理由．3《24.2.1 点和圆的位置关系》参考答案与试题解析一、选择题1．下列说法正确的是（）A．过一点A的圆的圆心可以是平面上任意点B．过两点A、B的圆的圆心在一条直线上C．过三点A、B、C的圆的圆心有且只有一点D．过四点A、B、C、D的圆不存在【解答】解：A、过一点A的圆的圆心可以是平面上任意点（A点外），故本选项错误，B、过两点A、B的圆的圆心在一条直线上，错误，C、正确，D、过四点A、B、C、D的圆可以存在，故本选项错误，故选：B．2．若△ABC的外接圆的圆心在△ABC的内部，则△ABC是（）A．锐角三角形B．直角三角形C．钝角三角形D．无法确定【解答】解：△ABC的外接圆的圆心在△ABC的内部，则△ABC是锐角三角形．故选A．3．在Rt△ABC中，∠C=90°，AC=6cm，BC=8cm，则它的外心与顶点C的距离为（）A．5cm B．6cm C．7cm D．8cm【解答】解：∵∠C=90°，AC=6cm，BC=8cm，∴AB==10cm，∵Rt△ABC的外心为斜边AB的中点，∴Rt△ABC的外接圆半径为5cm，∴它的外心与顶点C的距离为5cm．故选A．454．如图所示，一圆弧过方格的格点A 、B 、C ，试在方格中建立平面直角坐标系，使点A 的坐标为（﹣2，4），则该圆弧所在圆的圆心坐标是（ ）A ．（﹣1，2）B ．（1，﹣1）C ．（﹣1，1）D ．（2，1） 【解答】解：如图所示， ∵AW=1，WH=3， ∴AH==；∵BQ=3，QH=1， ∴BH==；∴AH=BH ， 同理，AD=BD ，所以GH 为线段AB 的垂直平分线， 易得EF 为线段AC 的垂直平分线， H 为圆的两条弦的垂直平分线的交点， 则BH=AH=HC ， H 为圆心．于是则该圆弧所在圆的圆心坐标是（﹣1，1）． 故选C ．65．Rt △ABC 中，∠C=90°，AC=2，BC=4，如果以点A 为圆心，AC 为半径作⊙A ，那么斜边中点D 与⊙A 的位置关系是（ ）A ．点D 在⊙A 外B ．点D 在⊙A 上C ．点D 在⊙A 内 D ．无法确定 【解答】解：根据勾股定理求得斜边AB==2，则AD=，∵＞2，∴点在圆外． 故选A ．6．若⊙A 的半径为5，圆心A 的坐标是（3，4），点P 的坐标是（5，8），你认为点P 的位置为（ ） A ．在⊙A 内 B ．在⊙A 上 C ．在⊙A 外 D ．不能确定 【解答】解：∵AP==2＜5，∴点P 在⊙A 内， 故选A ．7．如图，⊙O 是△ABC 的外接圆，若∠B=30°，AC=，则⊙O 的直径为（ ）A ．1B ．C ．2D ．【解答】解：作直径AD ，连结CD ，如图， ∵AD 为直径， ∴∠ACD=90°， ∵∠D=∠B=30°， ∴AD=2AC=2．故选D ．78．用反证法证明命题“三角形中必有一个内角小于或等于60°”时，首先应该假设这个三角形中（ ）A ．有一个内角小于60°B ．每一个内角都小于60°C ．有一个内角大于60°D ．每一个内角都大于60°【解答】解：用反证法证明“三角形中必有一个内角小于或等于60°”时， 应先假设三角形中每一个内角都不小于或等于60°，即每一个内角都大于60°． 故选：D ． 二、填空题9．点A 在以O 为圆心，3cm 为半径的⊙O 内，则点A 到圆心O 的距离d 的范围是 0≤d ＜3cm ． 【解答】解：∵点A 在以O 为圆心，3cm 为半径的⊙O 内， ∴点A 到圆心O 的距离d 的范围是：0≤d ＜3cm ． 故答案为：0≤d ＜3cm ．10．如图，在△ABC 中，∠ACB=90°，AC=2cm ，BC=4cm ，CM 为中线，以C 为圆心，cm 为半径作圆，则A 、B 、C 、M 四点在圆外的有 点B ； ，在圆上的有 点M ； ，在圆内的有 点A 、C ． ．【解答】解：∵△ABC 中，∠ACB=90°，AC=2cm ，BC=4cm ， ∴AB==2，∵CM 为中线， ∴CM=AB=，8∴AC ＜cm ，BC ＞cm ，∴在圆外的有点B ，在圆上的有点M ，在圆内的有点C 和点A ， 故答案为：点B ； 点M ； 点A 、C ．11．若AB=4cm ，则过点A 、B 且半径为3cm 的圆有 两 个．【解答】解：这样的圆能画2个．如图，作AB 的垂直平分线l ，再以点A 为圆心，3cm 为半径作圆交l 于O 1和O 2，然后分别以O 1和O 2为圆心，以3cm 为半径作圆， 则⊙O 1和⊙O 2为所求圆．故答案为：两．12．在△ABC 中，BC=24cm ，外心O 到BC 的距离为6cm ，则△ABC 外接圆的半径为 ．【解答】解：过O 作OD ⊥BC ，由垂径定理得， BD=BC=12cm ，在Rt △OBD 中，OD=6cm ，BD=12cm ， ∴OB==cm ，即△ABC 外接圆的半径为cm ．13．一点和⊙O 上的最近点距离为4cm ，最远距离为9cm ，则这个圆的半径是 6.5cm 或2.5cm ．9【解答】解：点P 应分为位于圆的内部与外部两种情况讨论：①当点P 在圆内时，最近点的距离为4cm ，最远点的距离为9cm ，则直径是4+9=13cm ，因而半径是6.5cm ；②当点P 在圆外时，最近点的距离为4cm ，最远点的距离为9cm ，则直径是9﹣4=5cm ，因而半径是2.5cm ．故答案为6.5cm 或2.5cm ．14．阅读下面材料：对于平面图形A ，如果存在一个圆，使图形A 上的任意一点到圆心的距离都不大于这个圆的半径，则称图形A 被这个圆所覆盖．回答下列问题： （1）边长为1cm 的正方形被一个半径为r 的圆所覆盖，r 的最小值是cm；（2）边长为1cm 的等边三角形被一个半径为r 的圆所覆盖，r 的最小值是cm ．【解答】解：（1）正方形ABCD 的边长为1cm ，则正方形ABCD 被一个半径为r 的圆所覆盖，r 的最小值为其外接圆的半径，如图1，正方形ABCD 的外接圆为⊙0， ∵∠B=90°， ∴AC 为直径， ∴AC=AB=，∴OA=，∴r 的最小值是cm ； （2）边长为1cm 的等边三角形ABC 被一个半径为r 的圆所覆盖，r 的最小值为其外接圆的半径，如图2，等边三角形ABC 的外接圆为⊙0， 连结OB ，作OD ⊥BC 于D ， ∵点O 为等边三角形ABC 的外心， ∴OB 平分∠ABC ， ∴∠OBD=30°，10∵OD ⊥BC ， ∴BD=BC=，在Rt △BOD 中，∵cos ∠OBD=，∴OB===，∴r 的最小值是cm ． 故答案为；．15．若Rt △ABC 的两条直角边a ，b 是方程x 2﹣3x+1=0的两根，则Rt △ABC 的外接圆面积是π．【解答】解：∵圆的半径r=c ，根据两直角边a 、b 分别是一元二次方程x 2﹣3x+1=0的两根，可得 a+b=3，a •b=1，∴c 2=a 2+b 2=（a+b ）2﹣2a •b=7， ∴Rt △的外接圆的面积为πr 2=π×（）2=π．故答案为：π． 三、解答题11 16．已知圆的半径等于5cm ，根据下列点P 到圆心的距离：（1）4cm ；（2）5cm ；（3）6cm ，判定点P 与圆的位置关系，并说明理由．【解答】解：（1）当d=4 cm 时，∵d ＜r ，∴点P 在圆内；（2）当d=5 cm 时，∵d=r ，∴点P 在圆上；（3）当d=6 cm 时，∵d ＞r ，∴点P 在圆外．17．在Rt △ABC 中，∠C=90°，BC=3m ，AC=4m ，以B 为圆心，以BC 为半径作⊙B ，D 、E 是AB 、AC 中点，A 、C 、D 、E 分别与⊙O 有怎样的位置关系？（画出图形，写过程）【解答】解：∵BC=3=R ，∴点C 在⊙B 上，∵AB=5＞3，∴点A 在⊙B 外，∵D 为BA 中点，∴， ∴点D 在⊙B 内，∵E 为AC 中点，∴， 连结BE ，∴BE===＞3m ， ∴E 在⊙B 外．1218．（教材变式题）如图所示，△ABC 中，AB=AC=10，BC=12，求△ABC 外接圆的半径．【解答】解：如图，作AD ⊥BC ，垂足为D ，则O 一定在AD 上，所以AD==8；设OA=r ，OB 2=OD 2+BD 2，即r 2=（8﹣r ）2+62，解得r=．答：△ABC 外接圆的半径为．19．如图，AD 为△ABC 外接圆的直径，AD ⊥BC ，垂足为点F ，∠ABC 的平分线交AD 于点E ，连接BD ，CD ．（1）求证：BD=CD ；（2）请判断B ，E ，C 三点是否在以D 为圆心，以DB 为半径的圆上？并说明理由．13 【解答】（1）证明：∵AD 为直径，AD ⊥BC ，∴由垂径定理得：∴根据圆心角、弧、弦之间的关系得：BD=CD ．（2）解：B ，E ，C 三点在以D 为圆心，以DB 为半径的圆上．理由：由（1）知：，∴∠1=∠2，又∵∠2=∠3，∴∠1=∠3，∴∠DBE=∠3+∠4，∠DEB=∠1+∠5，∵BE 是∠ABC 的平分线，∴∠4=∠5，∴∠DBE=∠DEB ，∴DB=DE ．由（1）知：BD=CD∴DB=DE=DC ．∴B ，E ，C 三点在以D 为圆心，以DB 为半径的圆上．（7分）20．某公园有一个边长为4米的正三角形花坛，三角形的顶点A 、B 、C 上各有一棵古树．现决定把原来的花坛扩建成一个圆形或平行四边形花坛，要求三棵古树不能移动，且三棵古树位于圆周上或平行四边形的顶点上．以下设计过程中画图工具不限．（1）按圆形设计，利用图1画出你所设计的圆形花坛示意图；（2）按平行四边形设计，利用图2画出你所设计的平行四边形花坛示意图；（3）若想新建的花坛面积较大，选择以上哪一种方案合适？请说明理由．14【解答】解：（1）（2）；（3）连接OB ，OA ，并延长AO 交BC 于D ， ∵r=OB==， ∴S ⊙O =πr 2=≈16.75，又S 平行四边形=2S △ABC =2××42×sin60°=8≈13.86， ∵S ⊙O ＞S 平行四边形，∴选择建圆形花坛面积较大．15。

24.2 与圆有关的位置关系 同步学习检测〔二〕班级 座号 姓名 ___ 得分一、选择题〔每题2分，共100分〕1．⊙O 的半径为5，点在直线上，且，直线与⊙O 的位置关系是〔 〕 A ．相切 B ．相交 C ．相离 D ．相切或相交 2．〔2021年清远〕O ⊙的半径r ，圆心O 到直线l 的距离为d ，当d r =时，直线l 与O ⊙的位置关系是〔 〕A ．相交 B ．相切 C ．相离 D ．以上都不对3．如图，在直角梯形ABCD 中，AD BC ∥，90C =∠，且AB AD BC >+，AB 是⊙O 的直径，那么直线CD 与⊙O 的位置关系为〔 〕A ．相离B ．相切C ．相交D ．无法确定 4．〔2021年孝感〕如图，⊙O 是△ABC 的外接圆，∠B =60°，那么∠CAO 的度数是( ) A ．15° B ．30° C ．45° D ．60°5.〔2021年天津市〕如图，ABC △内接于O ⊙，假设28OAB ∠=°，那么C ∠的大小为〔 〕A ． 28°B ．56°C ．60°D ．62°6.〔2021年凉山州〕如图，O ⊙是ABC △的外接圆，50ABO ∠=°，那么ACB ∠的大小为〔 〕A ．40°B ．30°C ．45°D ．50°7．(2021年潍坊)如图，圆O 的半径为R ，AB 是圆O 的直径，D 是AB 延长线上一点，DC 是圆O 的切线，C 是切点，连结AC ，假设30CAB ∠=°，那么BD 的长为〔 〕A ．2RBC ．RD8．〔2021年安徽〕△ABC 中，AB ＝AC ，∠A 为锐角，CD 为AB 边上的高，I 为△ACD 的内切圆圆心，那么∠AIB 的度数是〔 〕A ．120°B ．125°C ．135°D ．150°9.〔2021威海〕⊙O 是△ABC 的外接圆，假设AB =AC =5，BC =6，那么⊙的半径为〔 〕 A ．4 B ．3.25 C ．3.125 D ．2.25 10．〔09年山西省〕如图，AB 是⊙O 的直径，AD 是⊙O 的切线，点C 在⊙O 上，BC ∥OD ，AB ＝2,OD ＝3,那么BC 的长为〔 〕A ．23 B ．32C11．如图，⊙O 内切于△ABC ，切点为D 、E 、F ，假设∠B ＝50°，∠C ＝60°，•连结OE ，OF ，DE ，DF ，∠EDF 等于〔 〕 A ．45° B ．55° C ．65° D ．70° 12．〔09年邵阳市〕如图，AB 是⊙O 的直径，AC 是⊙O 的切线，A 为切点，连结BC 交圆0于点D,连结AD,假设∠ABC ＝450,那么以下结论正确的选项是〔 〕 A.AD ＝21BC B.AD ＝21AC C.AC ＞AB D.AD ＞DC 13. 〔2021年赤峰市〕如图PA 、PB 是⊙O 的切点，AC 是⊙O 的直径，∠P=40°，那么∠BAC得度数是 〔 〕 A 、10° B 、20° C 、30° D 、40°14．(2021年咸宁市)如图，在平面直角坐标系中，A ⊙与y 轴相切于原点O ，平行于x 轴的直线交A ⊙于M 、N 两点，假设点M 的坐标是(42)--，，那么点N 的坐标为〔 〕 A ．(12)--，B ．(12)-，C ．(152)--．，D ．(1.52)-，15. 〔2021年浙江省绍兴市〕如图，在平面直角坐标系中，P ⊙与x 轴相切于原点O ，平行于y 轴的直线交P ⊙于M ，N 两点．假设点M 的坐标是〔21-，〕，那么点N 的坐标是〔 〕A ．(24)-， B. (2 4.5)-， C.(25)-， D.(2 5.5)-，16．如图，在平面直角坐标系中，点A 在第一象限，⊙A 与轴相切于B ，与轴交于C 〔0，1〕， D 〔0，4〕两点，那么点A 的坐标是 〔 〕A.35(,)22B.3(,2)2C.5(2,)2D.53(,)2217．〔2021襄樊市〕如图，AB 是⊙O 的直径，点D 在AB 的延长线上，DC 切⊙O 于C ，假设25A =∠．那么D ∠等于〔 〕A ．40︒ B ．50︒ C ．60︒ D ．70︒ 18．如图，直线AB 、CD 相交于点O ，∠AOD=30°，半径为1cm 的⊙P 的圆心在射线OA 上，且与点O 的距离为6cm ．如果⊙P 以1cm/s 的速度沿由A 向B 的方向移动，那么〔 〕秒钟后⊙P 与直线CD 相切． Ａ．4 Ｂ．8 Ｃ．4或6 Ｄ．4或8 19．〔2021年佳木斯〕10、如图，AB 是⊙O 的直径，⊙O 交BC 的中点于D,DE⊥AC 于E,连接AD,那么以下结论正确的个数是( 〕①AD⊥BC ②∠EDA＝∠B ③OA＝12AC ④DE 是⊙O 的切线 A ．1 个 B ．2个 C ．3 个 D ．4个20．〔2021绵阳〕一个钢管放在V 形架内，右图是其截面图，O 为钢管的圆心．如果钢管的 半径为25 cm ，∠MPN = 60︒，那么OP =( )A ．50 cmB ．253cmC ．3350cm D ．503cm 21.〔2021年常德市〕如图，两个同心圆的半径分别为3cm 和5cm ，弦AB 与小圆相切于点C ，那么AB 的长为〔 〕 A ．4cm B ．5cm C ．6cm D ．8cm 22. 如图，以点O 为圆心的两个同心圆，半径分别为5和3，假设大圆的弦AB 与小圆相交，那么弦长AB 的取值范围是〔 〕A ．810AB ≤≤ B ．8AB ≥C ．810AB <≤D ．810AB << 23．〔09年陕西省)在如图中圆与圆之间不同的位置关系有 〔 〕A ．2种B ．3种C ．4种D ．5种 24．如图，⊙O 1 、⊙O 2 、⊙O 3两两相外切，⊙O 1的半径11r =，⊙O 2的半径22r =，⊙O 3的半径33r =，那么123O O O △是〔 〕A ．锐角三角形B ．直角三角形C ．钝角三角形D ．锐角三角形或钝角三角形 25．以下说法错误的选项是〔 〕A ．两圆仅有一个公共点时，两圆相切B ．两圆相交时，连心线垂直平分公共弦C ．两圆相切时，连心线必定经过切点D ．两圆没有公共点时，那么两圆外离 26．〔09年新疆乌鲁木齐市〕假设相交两圆的半径分别为1和2，那么此两圆的圆心距可能是〔 〕．A ．1 B ．2 C ．3 D ．4 27．〔2021年长春〕两圆的半径分别为2和5，圆心距为7，那么这两圆的位置关系为〔 〕 A ．外离 B ．外切 C ．相交 D ．内切 28．〔2021年泸州〕⊙O 1与⊙O 2的半径分别为5cm 和3cm ，圆心距020=7cm ，那么两圆的位置关系为〔 〕 A ．外离 B ．外切 C ．相交 D ．内切29．(2021年湖州)1O ⊙与2O ⊙外切，它们的半径分别为2和3，那么圆心距12O O 的长是〔 〕A ．12O O =1 B ．12O O ＝5 C ．１＜12O O ＜５ D ．12O O ＞５30．(2021年滨州)两圆半径分别为2和3，圆心距为d ，假设两圆没有公共点，那么以下结论正确的选项是〔 〕A ．01d <<B ．5d >C ．01d <<或5d >D ．01d <≤或5d > 31．〔2021年益阳市〕⊙O 1和⊙O 2的半径分别为1和4，如果两圆的位置关系为相交，那么圆心距O 1O 2的取值范围在数轴上表示正确的选项是32.〔关系为〔 〕 A ．外离 B ．外切 Ｃ．相交 D ．内含33.〔2021年舟山〕外切两圆的圆心距是7，其中一圆的半径是4，那么另一圆的半径是A ．11B ．7C ．4D ．334.〔2021年兰州〕两圆的半径分别为3cm 和2cm ，圆心距为5cm ，那么两圆的位置关系是〔 〕A ．外离 B ．外切 C ．相交 D ．内切 35．〔2021年赤峰市〕假设两圆的直径分别是2cm 和10cm ，圆心距为8cm ，那么这两个圆的位置关系是〔 〕 A.内切 B.相交 C.外切 D.外离36．〔2021肇庆〕假设1O ⊙与2O ⊙相切，且125O O =，1O ⊙的半径12r =，那么2O ⊙的B ． D ． A ．C ．半径2r 是〔 〕A ． 3 B ． 5 C ． 7 D ． 3 或7 37．〔2021临沂〕1O ⊙和2O ⊙相切，1O ⊙的直径为9C m ，2O ⊙的直径为4cm ．那么12O O 的长是〔 〕A ．5cm 或13cm B ．2.5cm C ．6.5cm D ．2.5cm 或6.5cm38.〔2021年宜宾〕假设两圆的半径分别是2cm 和3cm,圆心距为5cm ，那么这两个圆的位置关系是〔 〕A. 内切 B.相交 C.外切 D. 外离 39．平面直角坐标系中有点 A 〔3，4〕，以 A 为圆心，5为半径画圆，在同一坐标系中直线y ＝－x 与⊙A 的位置关系是〔 〕A ．相离B ．相切C ．相交D 以上情况都有可能40．(泸州市2021年)如图，PA 切⊙O 于A ，PO 交⊙O 于B ，假设PA=6，PB=4，那么⊙O 的半径是〔 〕A ．52B ．56C ．2D ．541．(南京市2021年)如图，⊙O 是等边三角形ABC 的外接圆，⊙O 的半径为2，那么等边三角形ABC 的边长为〔 〕ABC． D．42. (2021年潍坊市)如图，三角开ABC 内接于⊙O ，50A =∠，60ABC =∠，BD 是圆O 的直径， BD 交AC 于点E ，连结DC ，那么AEB ∠等于〔 〕A ．70B ．110 C ．90 D ．12043．(2021年浙江省嘉兴市)如图，正方形ABCD 中，E 是BC 边上一点，以E 为圆心、EC 为半径的半圆与以A 为圆心，AB 为半径的圆弧外切，那么BE ：AE 的值为〔 〕 A ．43B ．34 C ．45D ．3544．(浙江省丽水市2021年〕 如图，⊙O 是以数轴的原点O 为圆心，半径为1的圆， 45AOB ∠=︒,点P 在数轴上运动，假设过点P 且与OA 平行的直线与⊙O 有公共点, 设 OP x =，那么x 的取值范围是〔 〕A ．O≤x ≤2 B．≤x ≤2 C ．－1≤x ≤1 D ．x ＞2 45．(威海市2021年)如图，⊙O 的半径为2，点A 的坐标为〔2，32〕，直线AB 为⊙O 的切线，B 为切点．那么B 点的坐标为 〔 〕A ．⎪⎪⎭⎫ ⎝⎛-5823, B ．()13,- C ．⎪⎭⎫ ⎝⎛-5954, D ．()31,- 46．(泰州市2021年)如图，以直角梯形ABCD 的腰CD 为直径的半圆O 与梯形上底AD 、 下底BC 以及腰AB 均相切，切点分别是D 、C 、E 。

24.2.1 点和圆的位置关系同步测试一．选择题（共12小题）.1．用反证法证明命题：“已知△ABC，AB＝AC，求证：∠B＜90°．”第一步应先假设（）A．∠B≥90°B．∠B＞90°C．∠B＜90°D．AB≠AC2．已知⊙O的半径为6，点A与点O的距离为5，则点A与⊙O的位置关系是（）A．点A在圆外B．点A在圆内C．点A在圆上D．不确定3．在平面直角坐标系中，⊙O的直径为10，若圆心O为坐标原点，则点P（﹣8，6）与⊙O 的位置关系是（）A．点P在⊙O上B．点P在⊙O外C．点P在⊙O内D．无法确定4．已知△ABC内接于⊙O，连接AO并延长交BC于点D，若∠B＝60°，∠C＝50°，则∠BAD的度数是（）A．70°B．40°C．50°D．60°5．如图，已知AC是⊙O的直径，△ABC内接于⊙O，AB＝BC，∠DBC＝32°，则∠BCD ＝（）A．113°B．103°C．45°D．58°6．如图，⊙O为△ABC的外接圆，若∠BAC＝64°，则∠OBC等于（）A．36°B．32°C．26°D．24°7．已知点C为线段AB延长线上的一点，以A为圆心，AC长为半径作⊙A，则点B与⊙A的位置关系为（）A．点B在⊙A上B．点B在⊙A外C．点B在⊙A内D．不能确定8．如图，⊙O是△ABC的外接圆，已知∠ACB＝50°，则∠ABO的大小为（）A．30°B．40°C．45°D．50°9．如图，△ABC为圆O的内接三角形，AB为圆O的直径，点D在圆O上，∠BAC＝35°，则∠ADC的度数为（）A．45°B．50°C．55°D．65°10．如图，△ABC内接于⊙O，∠A＝50°．E是边BC的中点，连接OE并延长，交⊙O于点D，连接BD，则∠D的大小为（）A．55°B．65°C．60°D．75°二．填空题11．平面直角坐标系中，以原点O为圆心，2为半径作⊙O，则点A（2，2）与⊙O的位置关系为．12．在Rt△ABC中，∠ABC＝90°，AB＝6，BC＝8，则这个三角形的外接圆的直径长为．13．在平面直角坐标系xOy中，⊙O的半径为5，则点P（3，﹣4）在⊙O．（填“内”、“上”或“外”）14．用反证法证明“一个三角形中最多有一个内角是钝角”的第一步是．15．如图，△ABC内接于⊙O，BD是⊙O的直径，∠CBD＝21°，则∠A的度数为．三．解答题16．如图，网格纸中每个小正方形的边长为1，一段圆弧经过格点．（1）该图中弧所在圆的圆心D的坐标为；．（2）根据（1）中的条件填空：①圆D的半径＝（结果保留根号）；②点（7，0）在圆D（填“上”、“内”或“外”）；③∠ADC的度数为．17．已知线段AB＝6cm．（1）画半径为4cm的圆，使它经过A、B两点，这样的圆能画几个？（2）画半径为3cm的圆，使它经过A、B两点，这样的圆能画几个？（3）画半径为2cm的圆，使它经过A、B两点，这样的圆能画几个？18．如图，⊙O是地球的轴截面（把地球的轴截面近似地看成圆形），点P表示人造通讯卫星，已知从点P观测到地球表面的最近距离为P A＝akm，最远距离为PB＝bkm，其中b ＞a．用a、b表示地球的半径．参考答案1．解：用反证法证明命题：“已知△ABC，AB＝AC，求证：∠B＜90°．”第一步应先假设∠B≥90°．故选：A．2．解：∵OA＜R，∴点A在圆内，故选：B．3．解：∵点P的坐标为（﹣8，6），OP＝＝10∵⊙O的直径为10，半径为5∴点P在⊙O外．故选：B．4．解：延长AD交⊙O于E，连接CE，则∠E＝∠B＝60°，∠ACE＝90°，∴∠CAE＝90°﹣∠E＝90°﹣60°＝30°，∵∠B＝60°，∠ACB＝50°，∴∠BAC＝180°﹣∠B﹣∠ACB＝70°，∴∠BAD＝∠BAC﹣∠CAE＝40°．故选：B．5．解：∵AC是⊙O的直径，∴∠ABC＝90°，∵AB＝BC，∴∠ACB＝∠BAC＝45°，∴∠BDC＝45°，∵∠DBC＝32°，∴∠BCD＝180°﹣∠BDC﹣∠DBC＝180°﹣45°﹣32°＝103°．故选：B．6．解：∵⊙O为△ABC的外接圆，∠BAC＝64°，∴∠BOC＝2∠BAC＝2×64°＝128°，∵OB＝OC，∴∠OBC＝＝＝26°．故选：C．7．解：∵点C为线段AB延长线上的一点，∴AC＞AB，∴以A为圆心，AC长为半径作⊙A，则点B与⊙A的位置关系为点B在⊙A内，故选：C．8．解：∵∠ACB＝50°，∴∠AOB＝100°，∵AO＝BO，∴∠ABO＝（180°﹣100°）÷2＝40°，故选：B．9．解：∵AB是⊙O的直径，∴∠ACB＝90°，∵∠BAC＝35°，∴∠B＝90°﹣35°＝55°，∴∠ADC＝∠B＝55°．故选：C．10．解：连接CD，∵∠A＝50°，∴∠CDB＝180°﹣∠A＝130°，∵E是边BC的中点，∴OD⊥BC，∴BD＝CD，∴∠ODB＝∠ODC＝BDC＝65°，故选：B．11．解：∵点A（2，2）∴AO＝2，∵以原点O为圆心，2为半径作⊙O，∴2＞2，∴点A（2，2）与⊙O的位置关系为：圆外．故答案为：圆外．12．解：根据题意得：斜边是AC，即外接圆直径＝＝＝10，这个三角形的外接圆的直径长为10，故答案为：10．13．解：∵圆心P的坐标为（3，﹣4），∴OP＝＝5．∵⊙O的半径为5，∴点P（3，﹣4）在⊙O上．故答案为：上．14．解：用反证法证明“一个三角形中最多有一个内角是钝角”的第一步是假设至少有两个内角是钝角，故答案为：至少有两个内角是钝角．15．解：∵△ABC内接于⊙O，BD是⊙O的直径，∴∠BCD＝90°，∵∠CBD＝21°，∴∠A＝∠D＝90°﹣21°＝69°．故答案为：69°16．解：（1）根据垂径定理的推论：弦的垂直平分线必过圆心，可以作弦AB和BC的垂直平分线，交点即为圆心．如图所示，则圆心D的坐标为（2，0）；（2）①圆D的半径＝＝2，②点（7，0）在圆D外；③∠ADC的度数为90°．故答案为：（2，0），2，外，90°．17．解：（1）这样的圆能画2个．如图1：作AB的垂直平分线l，再以点A为圆心，4cm为半径作圆交l于O1和O2，然后分别以O1和O2为圆心，以4cm为半径作圆，则⊙O1和⊙O2为所求；（2）这样的圆能画1个．如图2：作AB的垂直平分线l，交AB于O点，然后以O为圆心，以3cm为半径作圆，则⊙0为所求；（3）这样的圆不存在．18．解：连接BO，延长P A一定交于点O，由题意可得：∠PBO＝90°，则设BO＝x，故AO＝x，则（a+x）2＝x2+b2，整理可得：x＝，即地球的半径为：．。