备战高考数学理母题小题精做系列第一季训练5 Word版无答案

专题24 综合训练31.集合2*{|70,}A x x x x N =-<∈，则*6{|,}B y N y A y=∈∈中元素的个数为（ ） A ． 1个 B ．2个 C ．3个 D ．4个 【答案】D 【解析】试题分析： 2*{|70,}A x x x x N =-<∈}6,5,4,3,2,1{=，}6,3,2,1{B =，因为B B A = ，∴集合2*{|70,}A x x x x N =-<∈，则*6{|,}B y N y A y=∈∈中元素的个数为4个． 考点：集合的表示方法. 2.下列说法错误的是（ ）A ．若p :R x ∈∃，210x x -+=，则:p x R ⌝∀∈， 210x x -+≠ B ．“:p x R∃∈1s i n 2θ=”是“30θ=或150”的充分不必要条件 C ．命题“若0a =，则0ab =”的否命题是“若0a ≠，则0ab ≠”D ．已知:p x R ∃∈，cos 1x =，:q x R ∀∈，210x x -+>，则“()p q ∧⌝”为假命题 【答案】B 【解析】考点：简易逻辑.3.在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，若2c =，b =30C =，则角B 等于（ ） A ．30 B ．60 C ．30或60 D ．60或120 【答案】D【解析】试题分析：因为2c =，b =30C =，所以由正弦定理可得：2322132cbsinCsinB =⨯==，因为c b >，可得：B )180,30(︒︒∈，所以︒︒=12060或B ．考点：1、正弦定理；2、特殊角的三角函数值.4.命题“[1,2]x ∀∈，20x a -≤”为真命题的一个充分不必要条件是（ ）A ．4a ≥B ．4a ≤ C.5a ≥ D ．5a ≤ 【答案】C 【解析】考点：1、充要条件；2、恒成立问题. 5.已知向量(sin(),1)6a πα=+，(4,4cos b α=，若a b ⊥，则4sin()3πα+=（ ） A．-．14-C. ．14【答案】B 【解析】试题分析：3cos 464sin b a -++=∙απα）（ 03)3sin(343cos 6sin 32=-+=-+=πααα，所以41)3sin(=+πα．所以41sin()sin()334ππαα+=-+=-． 考点：1、向量的数量积公式；2三角恒等变换公式. 6.设n S 是等差数列n a 的前n 项和，若612310S S =，则39S S =（ ） A ．16 B ．13 C.14D ．19 【答案】A 【解析】考点：等差数列性质.7.已知数列{}n a 中，45n a n =-+，等比数列{}n b 的公比q 满足1(2)n n q a a n -=-≥，且12b a =，则12||||||n b b b +++=（ ）A ．14n- B ．41n- C. 143n - D ．413n -【答案】B 【解析】试题分析：21q a 3a =-=-，1143)4(3--∙=-∙-=n n n b ，所以12||||||n b b b +++=1n 24343433-∙+⋅⋅⋅+∙+∙+1441413-=--∙=n n.考点：等差、等比数列通项公式及等比数列的前n 项和公式. 8.(1tan18)(1tan 27)++的值是（ ）A 【答案】C 【解析】试题分析：(1tan18)(1tan 27)++︒∙︒+︒+︒+=27tan 18tan 27tan 18tan 1227tan 18tan )27tan 18tan 1(45tan 1=︒︒+︒∙︒-∙︒+=．考点：两角和的正切公式的应用. 9.将函数sin(2)y x θ=+的图象向右平移6π个单位，得到的图象关于4x π=对称，则θ的一个可能的值为（ ） A ．23π B ．23π- C. 56π D ．56π-【答案】B 【解析】考点：1、函数)sin(φω+=x A y 的图象变换规律；2、正弦函数的图象的对称性. 10.在数列{}n a 中，12a =，22a =，且21(1)()n n n a a n N ++-=+-∈，则100S =（ ）A ．0B ．1300 C.2600 D ．2602 【答案】C 【解析】试题分析：由21(1)()n n n a a n N ++-=+-∈，当1n =时，得0a 13=-a ，即13a a =；当2n =时，得2a 24=-a ，由此可得，当n 为奇数时，1a a n =；当n 为偶数时，2222a n a n +-⨯=， ∴)()(10042993110021100a a a a a a a a a S +++++++=+++=[])98()4()2(5022221+++++++=a a a a a )9842(50502 ++++=a 2600=．考点：1、数列递推式；2、数列的分组求；3、等差数列的前n 项和. 11.在锐角ABC ∆中，若2A B =，则ab的范围是（a ，b 分别为角A ，B 的对边长）（ ）A ．B ． C.(0,2) D ． 【答案】A 【解析】试题分析：因为2A B =，B A 、为锐角，所以ππ<<B 32，,2B 20π<<所以46ππ<<B ，则a b ∈===cosB 2sinB B 2sin sin sin BA ．考点：1、倍角公式与正弦定理；2、三角形内角和定理.12.数列{}n a 满足1a =与11[]{}n n n a a a +=+（[]n a 与{}n a 分别表示n a 的整数部分与分数部分），则a=（）2014A．3020+．30203018 D．3018+【答案】B【解析】考点：数列项的求解.。

一、选择题（共6小题）1.【2013年普通高等学校招生全国统一考试（湖南卷）】复数()()1z i i i =+ 为虚数单位在复平面上对应的点位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2.【2013年普通高等学校统一考试试题新课标Ⅱ数学（理）卷】已知m ，n 为异面直线，m ⊥平面α，n ⊥平面β，直线l 满足l ⊥m ，l ⊥n ，,l α⊄l ,l β⊄则（）（A ）α∥β且l ∥α （B ）α⊥β且l ⊥β （C ）α与β相交，且交线垂直于l （D ）α与β相交，且交线平行于l3.【2013年普通高等学校招生全国统一考试（山东卷）理】过点()3,1作圆()2211x y -+=的两条切线，切点分别为,A B ，则直线AB 的方程为A.032=-+y xB.032=--y xC.034=--y xD.034=-+y x【答案】A【解析】画图可知直线AB 的斜率为负，其中一个切点为()1,1，代入A,D 只有A 满足.4.【2013年普通高等学校招生全国统一考试（北京卷）理】设关于x ,y 的不等式组210,0,0x y x m y m -+>⎧⎪+<⎨⎪->⎩表示的平面区域内存在点P (x 0，y 0)满足x 0－2y 0=2，求得m 的取值范围是 A.4,3⎛⎫-∞- ⎪⎝⎭ B. 1,3⎛⎫-∞ ⎪⎝⎭ C. 2,3⎛⎫-∞- ⎪⎝⎭ D. 5,3⎛⎫-∞- ⎪⎝⎭5.【2013年全国高考新课标（I ）理科】已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的右焦点为F (3,0)，过点F 的直线交椭圆于A 、B 两点.若AB 的中点坐标为(1，－1)，则E 的方程为 ( )A 、x 245＋y 236＝1B 、x 236＋y 227＝1错误！未找到引用源。

C 、x 227＋y 218＝1D 、x 218＋y 29＝16.【2013年普通高等学校招生全国统一考试福建卷】设T S ,是R 的两个非空子集，如果存在一个从S 到T 的函数)(x f y =满足：)(i {}S x x f T ∈=)(；)(ii 对任意S x x ∈21,，当21x x <时，恒有)()(21x f x f <，那么称这两个集合“保序同构”，以下集合对不是“保序同构”的是（ ）A. N B N A ==*,B. {}{}1008,31≤<-==≤≤-=x x x B x x A 或C. {}R B x x A =<<=,10 D. Q B Z A ==, 二、填空题（共2小题）7.【2013年普通高等学校招生全国统一考试（广东卷）理】若曲线ln y kx x =+在点()1,k 处的切线平行于x 轴,则k =______.【考点定位】导数的几何意义.8.【2013年普通高等学校招生全国统一考试（上海卷）理】在xOy平面上，将两个半圆弧22(3)1(3)x y x-+=≥、两条直线1-+=≥和22x y x(1)1(1)y=-围成的封闭图y=和1形记为D，如图。

专题11数列-备战2023年高考数学母题题源解密（全国通用）考向一等差数列【母题来源】2022年高考全国I 卷【母题题文】记n S 为数列{}n a 的前n 项和，已知11,n n S a a ⎧⎫=⎨⎬⎩⎭是公差为13的等差数列．（1）求{}n a 的通项公式；（2）证明：121112na a a +++<．【试题解析】【小问1详解】∵11a =，∴111S a ==,∴111S a =,又∵n n S a ⎧⎫⎨⎬⎩⎭是公差为13的等差数列，∴()121133n n S n n a +=+-=,∴()23n n n a S +=,∴当2n ≥时，()1113n n n a S --+=，∴()()112133n n nn n n a n a aS S --++=-=-,整理得：()()111n n n a n a --=+,即111n n a n a n -+=-,∴31211221n n n n n a a a a a a a a a a ---=⨯⨯⨯⋯⨯⨯()1341112212n n n n n n ++=⨯⨯⨯⋯⨯⨯=--，显然对于1n =也成立，∴{}n a 的通项公式()12n n n a +=；【小问2详解】()12112,11n a n n n n ⎛⎫==- ⎪++⎝⎭∴12111n a a a +++ 1111112121222311n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-=-< ⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦【命题意图】本题考查利用等差数列的通项公式、累乘法及裂项求和法.【命题方向】这类试题在考查题型选择、填空、解答题都有可能出现，多为中档题，是历年高考的必考题型．常见的命题角度有：（1）等差数列通项公式的求法；（2）等差数列前n 项和公式的求法；【得分要点】（1）掌握等差数列通项公式求法的几种形式；（2）掌握等差数列前n 项和公式求法的几种形式；考向二等比数列【母题来源】2022年高考全国乙卷（文科）【母题题文】已知等比数列{}n a 的前3项和为168，2542a a -=，则6a =（）A.14B.12C.6D.3【试题解析】详解：设等比数列{}n a 的公比为,0q q ≠，若1q =，则250a a -=，与题意矛盾，所以1q ≠，则()31123425111168142a q a a a qa a a q a q ⎧-⎪++==⎨-⎪-=-=⎩，解得19612a q =⎧⎪⎨=⎪⎩，所以5613a a q ==.故选：D .【命题意图】本题考查等比数列的通项公式的简单运算.【命题方向】这类试题在考查题型选择、填空、解答题都有可能出现，多为中档题，是历年高考的热点．常见的命题角度有：（1）等比数列通项公式的求法；（2）等比数列前n 项和公式的求法；【得分要点】（1）掌握等差数列通项公式的求法；（2）掌握等差数列前n 项和公式的求法；考向三等差数列、等比数列综合应用【母题来源】2022年高考全国甲卷（理科）【母题题文】记n S 为数列{}n a 的前n 项和．已知221nn S n a n+=+．（1）证明：{}n a 是等差数列；（2）若479,,a a a 成等比数列，求n S 的最小值．【试题解析】【小问1详解】解：因为221nn S n a n+=+，即222n n S n na n +=+①，当2n ≥时，()()()21121211n n S n n a n --+-=-+-②，①-②得，()()()22112212211n n n n S n S n na n n a n --+---=+----，即()12212211n n n a n na n a -+-=--+，即()()()1212121n n n a n a n ----=-，所以11n n a a --=，2n ≥且N*n ∈，所以{}n a 是以1为公差的等差数列．【小问2详解】解：由（1）可得413a a =+，716a a =+，918a a =+，又4a ，7a ，9a 成等比数列，所以2749a a a =⋅，即()()()2111638a a a +=+⋅+，解得112a =-，所以13n a n =-，所以()22112512562512222228n n n S n n n n -⎛⎫=-+=-=--⎪⎝⎭，所以，当12n =或13n =时()min 78n S =-．【命题意图】本题主要考查数列通项公式的求解，分组求和法，指数型裂项求和，错位相减求和等，属于中等题.【命题方向】这类试题在考查题型上主要以解答题的形式出现．多为中档题，数列是历年高考的热点，主要考查数列的通项公式及前n 项和.【得分要点】高考命制综合题时，常将等差、等比数列结合在一起，形成两者之间的相互联系和相互转化，破解这类问题的方法是首先寻找通项公式，利用性质之间的对偶与变式进行转化．一、单选题1．（江西省抚州市2021-2022学年高二下学期学生学业发展水平测试（期末）数学（理）试题）已知等差数列{}n a 的前n 项和为n S ，若2497330a a a a +++=，则11S =（）A ．44B ．33C ．66D ．55【答案】D 【解析】【分析】根据等差数列的通项公式和条件求出65a =，然后利用等差数列的求和可得答案.【详解】设等差数列{}n a 的公差为d ，因为{}n a 为等差数列，所以()()24791111163336865630a a a a a d a d a d a d a d a +++=+++++++=+==，得65a =，所以()1111161111552a a S a +===.故选：D.2．（重庆市长寿区2021-2022学年高二下学期期末数学（B ）试题）在等差数列{}n a 中，31124a a +=，则678a a a ++的值是（）A ．36B ．48C ．72D ．24【答案】A 【解析】【分析】利用等差中项的性质求得712a =，再由67873a a a a ++=即可得结果.【详解】由题设，1137224a a a +==，则712a =，所以6787336a a a a =++=.故选：A3．（北京市海淀区2021-2022学年高二下学期学业水平调研数学试题）已知{}n a 是等比数列，则“120a a >>”是“{}n a 为递减数列”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】A 【解析】【分析】由120a a >>求出公比的取值范围，然后结合等比数列的通项即可判断数列的单调性，举出反例说明{}n a 为递减数列不一定能得到120a a >>，再根据充分条件和必要条件即可得出答案.【详解】解：设数列{}n a 的公比为q ，若120a a >>，则110a a q >>，所以1q >，则110n n a a q -=<，11111nn n n a a q q a a q +-==>，所以1n n a a +<，所以{}n a 为递减数列；若{}n a 为递减数列，当111,22a q ==时，12n n a =，数列为递减数列，此时120a a >>，所以由{}n a 为递减数列不一定能得到120a a >>，所以“120a a >>”是“{}n a 为递减数列”的充分而不必要条件.故选：A.4．（广东省肇庆市2021-2022学年高二下学期期末数学试题）等比数列{}n a 中的项1a ，105a 是函数()32692f x x x x =-+-的极值点，则53a =（）A ．3B ．C ．D【答案】D 【解析】【分析】先根据题意确定函数的极值点，进而得到1105a a ⋅，然后根据等比中项求得答案.【详解】由题意，()()()23129313f x x x x x =-+=--'，则(),1x ∈-∞时()0f x '>，函数单调递增，()1,3x ∈时()0f x '<，函数单调递减，()3,x ∈+∞时()0f x '>，函数单调递增，于是x =1和x =3是函数的两个极值点，故1a ，105a 是()231290x x f x =-+='的两个根，所以11053a a ⋅=，所以25311053a a a =⋅=，又110540a a +=>，所以10a >，1050a >，设公比为q ，525310a a q =，所以55a =故选：D.5．（2022·上海奉贤·二模）若a ，b ，c ，d 成等比数列，则下列三个数列：①,,a b b c c d +++；②,,ab bc cd ；③,,a b b c c d ---，必成等比数列的个数为（）A ．0B ．1C ．2D ．3【答案】B 【解析】【分析】对于等比数列，注意相邻项加减所成的数列含0的情况判断①③即可.【详解】若a ，b ，c ，d 为1,1,1,1--，则,,a b b c c d +++不为等比数列，①不符合；由a ，b ，c ，d 必非零且公比为q ，则,,ab bc cd 也非零且公比为q ，②符合；若a ，b ，c ，d 为1,1,1,1，则,,a b b c c d ---不为等比数列，③不符合；故选：B6．（2022·陕西·西北工业大学附属中学模拟预测（理））已知数列{}n a 满足11a =，且()11n n n a a a +=+，*n ∈N ，则12233420202021a a a a a a a a ++++= （）A ．2021B ．20202021C ．202112D ．20212【答案】B 【解析】【分析】根据题意整理得1111n n a a +=+，结合等差数列通项公式可得1n a n =，再利用裂项相消1111n n a a n n +=-+运算处理．【详解】∵()11n n n a a a +=+，即11n n n a a a +=+，则11111n n n na a a a ++==+∴数列1n a ⎧⎫⎨⎬⎩⎭是以首项111a =，公差1d =的等差数列则111n n n a =+-=，即1n a n=∴()111111n n a a n n n n +==-++则122334202020211111120201 (223202*********)a a a a a a a a ++++=-+-++-= 故选：B ．7．（2022·全国·哈师大附中模拟预测（文））已知数列{}n a 满足11242n n a -=++++ ，则数列12n n n a a +⎧⎫⎨⎬⎩⎭的前5项和为（）A ．131B ．163C ．3031D ．6263【答案】D 【解析】【分析】先求出121n n a +=-，得到112112121n n n n n a a ++=---，利用裂项相消法求和.【详解】因为111124221,21n n n n n a a -++=++++=-=- ，所以()()()()()()1111121212211212121212121n n n n n n n n n n n n a a +++++---===-------.所以12n n n a a +⎧⎫⎨⎬⎩⎭前5项和为1223561611111111162121212121212121216363⎛⎫⎛⎫⎛⎫-+-++-=-=-= ⎪ ⎪ ⎪--------⎝⎭⎝⎭⎝⎭ 故选：D8．（2022·河南·模拟预测（理））《周髀算经》中有这样一个问题:冬至、小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气，自冬至日起，其日影长依次成等差数列，前三个节气日影长之和为28.5尺，最后三个节气日影长之和为1.5尺，今年3月20日17时37分为春分时节，其日影长为（）A ．4.5尺B ．3.5尺C ．2.5尺D ．1.5尺【答案】A 【解析】【分析】由题意构造等差数列{}n a ，设公差为d ，利用基本量代换求出通项公式，然后求7a .【详解】小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气日影长构成等差数列{}n a ，设公差为d ，由题意得：12310111228.51.5a a a a a a ++=⎧⎨++=⎩，解得：110.51a d =⎧⎨=-⎩所以()1111.5n a a n d n =+-=-，所以711.57 4.5a =-=，即春分时节的日影长为4.5.故选：A 【点睛】(1)数学建模是高中数学六大核心素养之一，在高中数学中，应用题是常见考查形式：求解应用性问题时，首先要弄清题意，分清条件和结论，抓住关键词和量，理顺数量关系，然后将文字语言转化成数学语言，建立相应的数学模型；(2)等差（比）数列问题解决的基本方法：基本量代换.9．（2022·上海市实验学校模拟预测）.定义“规范01数列”{}n a 如下：{}n a 共有2m 项，其中m 项为0，m 项为1，且对任意2k m ≤，12,,,k a a a 中0的个数不少于1的个数.若4m =，则不同的“规范01数列”共有（）A ．18个B ．16个C ．14个D ．12个【答案】C 【解析】【分析】根据数列新定义确定首末项分别为0、1，应用分类讨论及组合数求总排法数.【详解】依题意，由“规范01数列”得：第一项为0，第2m 项为1，当4m =时，只需确定中间的6个元素即可，且知中间的6个元素有3个“0”和3个“1”.①若0后接00，如：0001.后面四个空位可以随意安排3个1和1个0，则有34C 种；②若0后接01，如：0011.后面四个空位可以排的数字为2个“0”和2个“1”，只有一种情形不符合题意，即01后面紧接11，除此外其它的情形故满足要求，因此排法有24C 15-=种；③若0后接10，如：010 1.在10后若接0，则后面有13C 种；在10后若接1，即010101，第五个数字一定接0，另两个位置0、1随意排，有22A 种；综上，满足题意的排法有312432C 5C A 14+++=种.故选：C.10．（2022·山西太原·三模（理））斐波那契数列，又称黄金分割数列，该数列在现代物理、准晶体结构、化学等领域有着非常广泛的应用，在数学上，斐波那契数列是用如下递推方法定义的：121a a ==，()*123,.n n n a a a n n N --=+≥∈已知2222123mma a a a a ++++ 是该数列的第100项，则m =（）A ．98B ．99C ．100D ．101【答案】B 【解析】【分析】根据题意推出2121a a a =，222321a a a a a =-，L ，211m m m m m a a a a a +-=-，利用累加法可得211mi m m i a a a +==∑，即可求出m 的值.【详解】由题意得，2121a a a =，因为12n n n a a a --=-，得222312321()a a a a a a a a =-=-，233423432()a a a a a a a a =-=-，L ，21111()m m m m m m m m a a a a a a a a +-+-=-=-，累加，得222121m m m a a a a a ++++= ，因为22212m ma a a a +++ 是该数列的第100项，即1m a +是该数列的第100项，所以99m =.故选：B.二、填空题11．（2022·四川省内江市第六中学模拟预测（理））已知数列{}n a 满足12a =，24a =，2(1)3+-=-+nn n a a ，则数列{}n a 的前20项和为___________.【答案】330【解析】【分析】分别讨论n 为奇数时，数列{}21n a -的通项公式与n 为偶数时，数列{}2n a 的通项公式，再利用分组求和法代入求和即可.【详解】由题意，当n 为奇数时，2(1)32n n a a +-=-+=，所以数列{}21n a -是公差为2，首项为2的等差数列，所以2122(1)2n n a n -=+-=，当n 为偶数时，2134n n a a +-=+=，所以数列{}2n a 是公差为4，首项为4的等差数列，所以244(1)4n n n a =+-=，()()20122013192420......S a a a a a a a a a =+++=+++++++ 10(220)10(440)(2420)(4840)33022++=+++++++=+= ，故答案为：33012．（2022·青海·海东市第一中学模拟预测（理））设等比数列{}n a 的前n 项和为n S ，若241252a a a =，且61224S S S λ+=，则λ＝________.【答案】143【解析】【分析】项和公式来进行相关运算即可.【详解】∵241252a a a =，∴22852a a =，∴62q =，∵61224S S S λ+=，∴()()()61224111111111a q a q a q q q q λ---+⋅=---，()61224111q q q λ-+-=-，将62q =代入，可得143λ=.故答案为：14313．（2022·江西·临川一中模拟预测（文））已知23n a n n =+，若2n n a λ≤对于任意*n ∈N 恒成立，则实数λ的取值范围是_______．【答案】15,4⎡⎫+∞⎪⎢⎣⎭【解析】【分析】先分离参数将问题转化为232n n n λ+≤对于任意*n ∈N 恒成立，进而转化为2max 3()2n n n λ+≤，构造232n nn n b +=，再作差判定单调性求出数列{}n b 的最值，进而求出λ的取值范围.【详解】因为23n a n n =+，且2n n a λ≤对于任意*n ∈N 恒成立，所以232nn n λ+≤对于任意*n ∈N 恒成立，即2max 3()2n n n λ+≤，令232n n n n b +=，则2221113(1)(1)3354222n n n n n n n n n n n b b +++++++-++-=-=，因为21302b b -=>，32104b b -=>，43102b b -=-<，且21135402n n n n n b b ++-++-=<对于任意3n ≥恒成立，所以12345b b b b b <<>>>⋅⋅⋅，即2max 3315()24n n n b +==，所以实数λ的取值范围是15,4⎡⎫+∞⎪⎢⎣⎭.故答案为：15,4⎡⎫+∞⎪⎢⎣⎭.三、解答题14．（2022·全国·模拟预测）已知数列{}n a 的前n 项和为n S ，14a =，28a =，且2124n n n S S S ++-+=．(1)求证：数列{}n a 是等差数列；(2)若m a ，m S ，114m a +成等比数列，求正整数m ．【答案】(1)证明见解析(2)7【解析】【分析】（1）根据11n n n a S S ++=-化简整理，解得等差数列定义1n n a a d +-=处理；（2）根据()11n a a n d +-=，()12n n n a a S +=，并代入2114m m m S a a +=运算求解．(1)因为2124n n n S S S ++-+=，所以2114n n n n S S S S +++--+=，即()()2114n n n n S S S S +++---=，则214n n a a ++-=．又14a =，28a =，满足214a a -=，所以{}n a 是公差为4的等差数列．(2)由（1）得，()4144n a n n =+-⨯=，则()244222n n n S n n +==+．又2114m m m S a a +=，所以()()222214441,N m m m m n ++=⨯⨯+∈，化简得2560m m +-=，解得m ＝7或8m =-（舍）．所以m 的值为7．15．（2022·全国·模拟预测）已知{}n a 是等比数列，0n a >，1329a a a =，12312323a a a ++=．(1)求{}n a 的通项公式；(2)记n S 为数列{}n a 的前n 项和，求使得1n n S na +≥的正整数n 的所有取值．【答案】(1)3n n a =或9n a =；(2)答案见解析．【解析】【分析】（1）设{}n a 的公比为()0q q >，由等比数列的性质，列出方程即可解出29a =，3q =或1q =，从而得出{}n a 的通项公式；（2）由等比数列前n 项和公式求出n S ，即可解出不等式1n n S na +≥．(1)因为{}n a 为等比数列，所以213229a a a a ==，又0n a ≠，所以29a =．设{}n a 的公比为()0q q >，因为12312323a a a ++=，所以12329993q q++=，化简得24309q q q -+=，解得3q =或1q =．当3q =时，2933n n n a -=⨯=．当1q =时，9n a =．(2)当3q =时，()1113312n n n a q S q +--==-．由1n n S na +≥，得23332n n n +-≥⋅，化简得()9233n n -⨯≥．易知，当5n ≥时，不等式显然不成立，检验可知，满足不等式的正整数n 的所有取值为1，2，3，4．当1q =时，9n S n =，由1n n S na +≥，得()919n n +≥，此时n 的取值为一切正整数．16．（2022·江苏·扬中市第二高级中学模拟预测）已知数列{}n a 满足111,31n n a a a +==+.(1)证明12n a ⎧⎫+⎨⎬⎩⎭是等比数列，并求{}n a 的通项公式；(2)证明：121113 (2)n a a a +++<.【答案】（1）证明见解析，113322n n a -+=；（2）证明见解析.【解析】【详解】试题分析：本题第（1）问，证明等比数列，可利用等比数列的定义来证明，之后利用等比数列，求出其通项公式；对第（2）问，可先由第（1）问求出1na ，然后转化为等比数列求和，放缩法证明不等式.试题解析：（1）证明：由131n n a a +=+得1113()22n n a a ++=+，所以112312n n a a ++=+，所以12n a ⎧+⎫⎨⎬⎩⎭是等比数列，首项为11322a +=，公比为3，所以12n a +=1332n -⋅，解得n a =312n -.（2）由（1）知：n a =312n -，所以1231n n a =-，因为当1n ≥时，13123n n --≥⋅，所以1113123n n -≤-⋅，于是11a +21a + 1n a =31(1)23n -32<，所以11a +21a + 1n a 32<.【易错点】对第（1）问，构造数列证明等比数列不熟练；对第（2）问，想不到当1n ≥时，13123n n --≥⋅，而找不到思路，容易想到用数学归纳法证明而走弯路.考点：本小题考查等比数列的定义、数列通项公式的求解、数列中不等式的证明等基础知识，考查同学们的逻辑推理能力，考查分析问题与解决问题的能力.数列是高考的热点问题之一，熟练数列的基础知识是解决好该类问题的关键.。

『高考真题•母题解密」『分项汇编•逐一击破J专题05统计【母题来源一】［2020年高考全国I 卷理数】某校一个课外学习小组为研究某作物种子的发 芽率y 和温度x （单位：°C ）的关系，在20个不同的温度条件下进行种子发芽实验，由实B.y = a + bx 1D. y = a + blnx【答案】D 【解析】由散点图分布可知，散点图分布在一个对数函数的图象附近, 因此，最适合作为发芽率y 和温度x 的回归方程类型的是y = a+b\nx. 故选D.【名师点睛】本题考查函数模型的选择，主要观察散点图的分布，属于基础题.根据散点图 的分布可选择合适的函数模型.【母题来源二】［2018年高考全国I 卷理数】某地区经过一年的新农村建设，农村的经济收 入增加了一倍，实现翻番.为更好地了解该地区农村的经济收入变化情况，统计了该地区新 农村建设前后农村的经济收入构成比例，得到如下饼图:母题呈现A. y = a + bx C. y = a + be x验数据乂）。

= 1,2, ,20）得到下面的散点图:的回归方程类型的是建设前经济收入构成比例建设后经济收入构成比例则下面结论中不正确的是A. 新农村建设后，种植收入减少B. 新农村建设后，其他收入增加了一倍以上C. 新农村建设后，养殖收入增加了一倍D. 新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半 【答案】A【解析】设新农村建设前的收入为而新农村建设后的收入为2M,则新农村建设前种植 收入为0.6M,而新农村建设后的种植收入为0.74M,所以种植收入增加了，所以A 项不正 确； 新农村建设前其他收入为0.04M,新农村建设后其他收入为0.1M,故增加了一倍以上，所 以B 项正确；新农村建设前，养殖收入为0.3M,新农村建设后为0.6M,所以增加了一倍，所以C 项正确; 新农村建设后，养殖收入与第三产业收入的综合占经济收入的30%+ 28% = 58% > 50%, 所以超过了经济收入的一半，所以D 正确. 故选A.母题揭秘【命题意图】会利用散点图认识变量间的相关关系，了解回归分析的基本思想、方法及其简单应用. 【命题规律】 高考常考查知识点：（1）会作两个有关联变量的数据的散点图，会利用散点图认识变量间的相关关系. (2) 了解最小二乘法的思想，能根据给出的线性回归方程系数公式建立线性回归方程. (3)了解分布的意义和作用，会列频率分布表，会画频率分布直方图、频率折线图、茎叶 图，4%其他收入种植收入养殖收入 第三产业收入役\第二产业收入种植收入 养殖收入其他收入理解它们各自的特点.能从样本数据中提取基本的数字特征(如平均数、标准差)，并给出合理的解释.【答题模板】对某些特殊的非线性关系，可以通过变量转换，把非线性回归问题转化成线性回归问题，然后用线性回归的方法进行研究.在大量的实际问题中，所研究的两个变量不一定都呈线性相关关系，当两变量y与x不具有线性相关关系时，要借助散点图，与己学过的函数(如指数函数、对数函数、蓦函数等)的图象相比较，找到合适的函数模型，利用变量代换转化为线性函数关系，从而使问题得以解决.【方法总结】1•相关关系的判断判定两个变量正、负相关性的方法：(1)画散点图：若点的分布从左下角到右上角，则两个变量正相关；若点的分布从左上角到右下角，则两个变量负相关；(2)相关系数：r>0时，正相关；r<0时，负相关；(3)线性回归方程中：片>0时，正相关；片<°时，负相关.2.求回归直线方程的一般步骤：(1)作出散点图，依据问题所给的数据在平面直角坐标系中描点，观察点的分布是否呈条状分布，即是否在一条直线附近，从而判断两变量是否具有线性相关关系.(2)当两变量具有线性相关关系时，求回归系数余片，写出回归直线方程.(3)根据方程进行估计.3.求非线性回归方程的步骤：(1)确定变量，作出散点图.(2)根据散点图，选择恰当的拟合函数.(3)变量置换，通过变量置换把非线性回归问题转化为线性回归问题，并求出线性回归方程.(4)分析拟合效果：通过计算相关指数或画残差图来判断拟合效果.（5）根据相应的变换，写出非线性回归方程.4.频率分布直方图（1）画频率分布直方图的步骤①求极差（即一组数据中最大值与最小值的差）；②决定组距与组数；③将数据分组；④列频率分布表；⑤画频率分布直方图（以横轴表示样本分组，纵轴表示频率与组距的比值）.（2）频率分布直方图的性质①落在各小组内的频率用各小长方形的面积表示，且各小长方形的面积的和等于1.②频率分布直方图与众数、中位数与平均数的关系a.最高的小长方形底边中点的横坐标即是众数；勿中位数左边和右边的小长方形的面积和是相等的；c.平均数是频率分布直方图的“重心”，等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标的和.1.[2020届全国100所名校高考模拟金典卷高三数学（十一）试题】已知某产品的销售额y 与广告费用X之间的关系如下表：若求得其线性回归方程为y^6.5x+a,则预计当广告费用为6万元时的销售额为（）A.42万元B. 45万元C.48万元D. 51万元【答案】C【解析】由题意，根据上表中的数据，可得x =2, y = 22，即回归方程经过样本点中心（元,予），又由线性回归方程为宁= 6.5x + a,所以22 = 6.5x2 + a,解得。

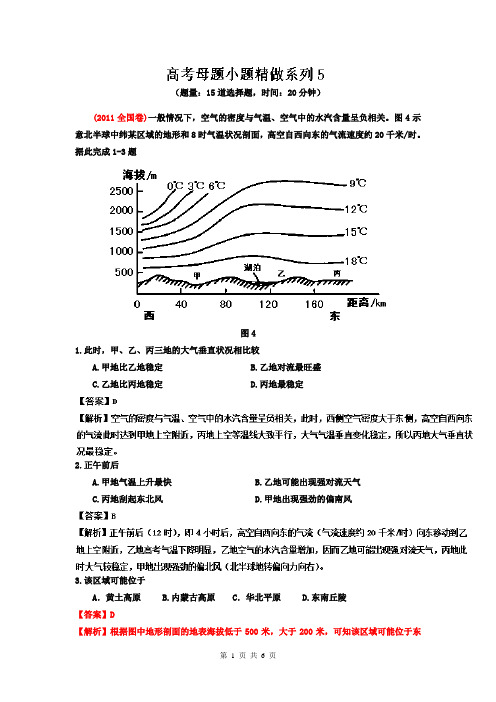
（题量：15道选择题，时间：20分钟）(2011全国卷)一般情况下，空气的密度与气温、空气中的水汽含量呈负相关。

图4示意北半球中纬某区域的地形和8时气温状况剖面，高空自西向东的气流速度约20千米/时。

据此完成1-3题图41.此时，甲、乙、丙三地的大气垂直状况相比较A.甲地比乙地稳定B.乙地对流最旺盛C.乙地比丙地稳定D.丙地最稳定2.正午前后A.甲地气温上升最快B.乙地可能出现强对流天气C.丙地刮起东北风D.甲地出现强劲的偏南风3.该区域可能位于A．黄土高原 B.内蒙古高原C．华北平原 D.东南丘陵【答案】D【解析】根据图中地形剖面的地表海拔低于500米，大于200米，可知该区域可能位于东南丘陵，黄土高原和内蒙古高原海拔高于1000米，华北平原海拔多低于200米。

（2011浙江卷）某校学生于台风过后，前往某山区实习，观测溪谷的变化情况。

图1为学生实习地区的等高线地形图。

完成4-5题。

4.学生在实习中可以得知的是A.溪谷的坡度；溪谷的蒸发量B.溪谷的蒸发量；溪流的水深和流速C.溪谷的台风降雨量；堆积物粒径大小D.溪谷的坡度；堆积物粒径大小(2012海南卷)图4a是2005年某城市新区规划图。

针对规划实施中出现的一些问题，2010年对原规划进行了修编（图4b）。

该城市盛行西北风。

据此完成6-8题。

6. 按主导职能，该新区规划为（）A. 居住区B. 文化区C. 政务区D. 工业区7. 在图4b中的M处适宜修建（）A. 自来水厂B. 垃圾焚烧厂C. 污水处理厂D. 热电厂8. 据图文资料推测，该新区规划实施中出现的主要问题是A. 交通拥堵B. 环境破坏严重C. 公共服务配套不足D. 工业用地不足(2012江苏卷)我国东南沿海某市原为农产品和部分轻工业原料生产基地，1990年开始积极吸引外资，调整产业结构，建立起以化工、机械、纺织、电子、服装等为主的工业体系。

图7是该市1990—2010年产业结构变化图。

专题05新农村建设——治沟造地【母题来源】2020年新课标全国卷Ⅰ【母题题文】治沟造地是陕西省延安市对黄土高原的丘陵沟壑区，在传统打坝淤地的基础上，集耕地营造、坝系修复、生态建设和新农村发展为一体的“田水路林村”综合整治模式，实现了乡村生产、生活、生态协调发展（图1）。

据此完成1~3题。

图11．与传统的打坝淤地工程相比，治沟造地更加关注A．增加耕地面积B．防治水土流失C．改善人居环境D．提高作物产量2．治沟造地对当地生产条件的改善主要体现在A．优化农业结构B．方便田间耕作C．健全公共服务D．提高耕地肥力3．推测开展治沟造地的地方①居住用地紧张②生态环境脆弱③坡耕地比例大④农业生产精耕细作A．①③B．①④C．②③D．②④【试题解析】【答案】1．C2．B3．C【解析】1．结合所学知识可知，传统的打坝淤地就是为了防治水土流失，且增加了耕地面积，提高了作物产量。

结合图示信息可看出，治沟造地不仅拦截泥沙、增加了耕地面积，且注重生态建设和新农村的发展，因此治沟造地更加关注改善人居环境，C对。

2．该题关键是注意审题，抓住关键词“生产条件”，AC可直接排除。

原有黄土高原农田是沿着沟坡分布，条块分割，高低不平。

结合图示“沟道覆土造地”信息可知，治沟造地后，沟道被治理为一块块平整的良田，规模成片且平整，更有利于改善耕作条件，利于田间管理耕作，B对。

提高耕地肥力没体现，D错。

3．根据图中信息提示：复垦空废宅基地和易地移民搬迁，说明该地居住用地不紧张，排除①；位于黄土高原丘陵沟壑区，说明生态环境脆弱，②对；加上坡面退耕还林，治沟造地，说明坡耕地比例大，农业生产精耕细作图中没有体现出来，所以选C。

【命题意图】新中国成立以来，黄土高原治理先后经历坡面治理，沟坡联合治理，以及小流域综合治理和退耕还林还草工程等阶段，每一阶段均取得显著成效。

但是黄土高原局部地区过度退耕还林还草，导致人-地-粮食关系的矛盾日益凸显，乡村“空心化”日趋严重，农村不可持续发展问题日益突出。

专题一经典母题30题(第一期)1．设复数11z i=-，则z 的共轭复数是( ) A ．11i +B ．1i +C ．11i-D ．1i - 【答案】D【解析】由题可知，i i ii z +=-=-=11112，故z ＝1＋i 的共轭复数为z ＝1－i ；2．已知函数()223f x x x =-++，若在区间[]4,4-上任取一个实数0x ，则使()00f x ≥成立的概率为()A ．1【答案】B【解析】因为f (x 0)≥0，所以－x 02＋2x 0＋3≥0，解得：－1≤x 0≤3，所以使f (x 0)≥0成立的B ．317个项中，整式的个数是()A ．1B ．3C ．5D ．7 【答案】B【解析】二项展开式的通项为，(,016)k Z k ∈≤≤，要使得它为整式，则k ＝6，8，10，故有三项，选B .4．在边长为1的正三角形ABC 中，设2BC BD = ，CA CE λ= ，若，则λ的值为()(A B )2(C D )3【答案】C【解析】由题意可得：5.设ABC∆的内角A，B，C所对边的长分别是a，b，c，且3b=，1c=，2A B=.则a 的值为()(A B C D【答案】D【解析】由题意可知：BbaBBABA cos2cossin2sin2sinsin=⇒=⇒=，所以，由余弦定理可得：Baccab cos2222-+=即122=a，6.(0ω>)的图象分别向左.向右各平移图象的对称轴重合，则ω的最小值为()A.1C.2D.4【答案】Cω＞0)为y＝2ω＞0)的图象向右平移个单位后，所得图像的解析式为②，解①得=0ω不合题意，解②得：ω＝2k ，k ∈Z ，则ω的最小值为2，故选C7.如图所示的程序框图输出的所有点都在函数()A ．1+=x y 的图像上B ．x y 2=的图像上C ．xy 2=的图像上 D ．12-=x y 的图像上【答案】D【解析】由题可知，输入x ＝1，y ＝1，由于1≤4，输出点(1，1)，进入循环， x ＝1＋1＝2，y ＝2×1＝2，由于2≤4，输出点(2，2)，进入循环， x ＝2＋1＝3，y ＝2×2＝4，由于3≤4，输出点(3，4)，进入循环， x ＝3＋1＝4，y ＝2×4＝8，由于4≤4，输出点(4，8)，进入循环，x ＝4＋1＝5＞4，循环结束；故点(2，2)，点(3，4)点(4，8)满足均在函数12-=x y 的图像上；8.对于三次函数f (x )＝ax 3＋bx 2＋cx ＋d (a ≠0)，给出定义：设f '(x )是函数y ＝f (x )的导数，f ''(x )是f '(x )的导数，若方程f ''(x )＝0有实数解x 0，则称点(x 0，f (x 0))为函数y ＝f (x )的“拐点”．某同学经过探究发现：任何一个三次函数都有“拐点”，任何一个三次函数都有对称中心，且“拐点”就是对称中心。

一、选择题（共6小题）1.【2013年普通高等学校招生全国统一考试（山东卷）】给定两个命题p ，q ,若p ⌝是q 的必要而不充分条件，则p 是q ⌝的A.充分不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件2.【2013年普通高等学校招生全国统一考试(江西卷)理】总体由编号为01，02，…，19，20的20个个体组成.利用下面的随机数表选取5个个体，选取方法从随机数表第1行的第5列和第6列数字开始由左到右一次选取两个数字，则选出来的第5个个体的编号为 （ ） 7816 6572 0802 6314 0702 4369 9728 0198 3204 9234 4934 8200 3623 4869 6938 7481A.08B.07C.02D.013.【2013年普通高等学校招生全国统一考试福建卷理】阅读如图所示的程序框图，若编入的10=k ，则该算法的功能是（ ）A. 计算数列{}12-n 的前10项和B.计算数列{}12-n 的前9项和C. 计算数列{}1-2n 的前10项和D. 计算数列{}1-2n 的前9项和4.【2013年普通高等学校招生全国统一考试（辽宁卷）理科】下面是关于公差0d >的等差数列{}n a 的四个命题：{}1:n p a 数列是递增数列；{}2:n p na 数列是递增数列； 3:n a p n ⎧⎫⎨⎬⎩⎭数列是递增数列； {}4:3n p a nd +数列是递增数列； 其中的真命题为（A ）12,p p （B ）34,p p （C ）23,p p （D ）14,p p5.【2013年普通高等学校招生全国统一考试（四川卷）理科】函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示，则,ωϕ的值分别是（ ）（A ）2,3π- （B ）2,6π- （C ）4,6π- （D ）4,3π6.【2013年普通高等学校招生全国统一考试（陕西卷）】在如图所示的锐角三角形空地中, 欲建一个面积不小于300m 2的内接矩形花园(阴影部分), 则其边长x(单位m)的取值范围是 （ ）(A) 【15,20】 (B) 【12,25】 (C) 【10,30】 (D) 【20,30】二、填空题（共2小题）7.【2013年普通高等学校招生全国统一考试（四川卷）理科】二项式5()x y +的展开式中，含23x y 的项的系数是____________.（用数字作答）8.【2013年普通高等学校招生全国统一考试（四川卷）理科】在平行四边形ABCD 中，对角线AC 与BD 交于点O ，AB AD AO λ+=u u u r u u u r u u u r ，则λ=____________.。