当前位置：文档之家 › 工程力学第三章 受力分析

工程力学第三章 受力分析

  • 格式：ppt
  • 大小：1.17 MB
  • 文档页数：42

下载文档原格式

  / 42

合集下载

工程力学第三章 受力分析(课堂PPT)

工程力学第三章 受力分析(课堂PPT)


1
31
解：
1.杆AB的受力图。
2. 活塞和连杆的受力图。
E D
B
Aq
C q
B
FBA
A
FA
3. 压块 C 的受力图。
q
FCB
FAB
q
C FCx
F
B
q
FBC
1 FCy
32
例题7
D
A
K
q
C
E
BⅠ Ⅱ
P
如图所示平面构架，由杆AB ， DE及DB铰接而成。钢绳一端拴 在K处，另一端绕过定滑轮Ⅰ和 动滑轮Ⅱ后拴在销钉B上。重物 的重量为P，各杆和滑轮的自重 不计。（1）试分别画出各杆， 各滑轮，销钉B以及整个系统的 受力图；（2）画出销钉B与滑轮 Ⅰ一起的受力图；（3）画出杆 AB ，滑轮Ⅰ ，Ⅱ ，钢绳和重物 作为一个系统时的受力图
处必有力，力的方向由约束类型而定。
要注意力是物体之间的相互机械作用。因此对 2、不要多画力 于受力体所受的每一个力，都应能明确地指出
它是哪一个施力体施加的。
1
18
3、不要画错力的方向 约束反力的方向必须严格地按照约束的类型来画，不 能单凭直观或根据主动力的方向来简单推想。在分析 两物体之间的作用力与反作用力时，要注意，作用力 的方向一旦确定，反作用力的方向一定要与之相反， 不要把箭头方向画错。
BB
D
F
A
C
1
7
解： 1. 杆 BC 的受力图。
BB
D
F
A
C
1
FB B
C
FC
8
2. 杆AB 的受力图。
BB
D
F
A
正交分解
03结构简图和物体受力分析(工程力学基础)

03结构简图和物体受力分析(工程力学基础)


四、支座的简化
1、支座简化示例 固定铰支座、可动铰支座、固定端支座、定向支座等都是理想的支 座。为便于计算，要分析实际结构支座的主要约束功能与哪种理想 支座的约束功能相符合，将工程结构的实际支座简化为力学中的理 想支座。 图（a）中所示的是预制钢筋混凝土柱与杯形基础的连接形式。基 础下面是比较坚实的地基，如杯口四周填人沥青麻丝，荷载的作用 能使柱端发生微小转动，其约束功能基本上与固定铰支座相符合， 则可简化为固定铰支座，如图（b）所示。如将预制钢筋混凝土柱插 在较深的杯形基础中，杯口四周及底部用细石混凝土填实，如图（c ）所示，柱端被相当坚实地固定住，其约束功能基本上与固定支座 相符合，则可简化为固定端支座，如图（d）所示。
位移的条件。
5
§3-2 平面体系的几何组成分析
１、几何可变体系：在荷载作用下 不能保持其几何形状和位置都不改 变的体系。
２、几何不变体系：在荷载作用下 能保持其几何形状和位置都不改变 的体系。
3、刚片 平面内的刚体称为刚片 4、自由度 体系可独立运动的方式称为该体系的自由度。
或表示体系位置的独立坐标数。 平面体系的自由度：用以确定平面体系在平面
六、计算跨度
计算简图的选取案例
七、平面杆系结构的分类
（一）按结构形式分
（1）梁式结构 ：梁由受弯杆件构成，杆件轴线一般为直线。 （2）刚架结构 ： 刚架是由梁和柱组成的结构。 （3）桁架结构 ： 桁架是由若干直杆在两端用铰链连接组成的结
构。。 （4）拱结构 ： 拱一般由曲杆构成。 （5）组合结构： 组合结构是桁架和梁或刚架组合在一起形成的
两刚片规则例
规则二：三刚片规则
三个刚片用不全在一条直线上的 三个单铰（可以是虚铰）两两相 连，组成无多余约束的几何不变 体系。如图所示。 铰接三角形规则：简称三角形规 则
工程力学中的杆件受力分析和应力分布

工程力学中的杆件受力分析和应力分布

工程力学中的杆件受力分析和应力分布工程力学是研究物体在受力作用下的力学行为及其工程应用的学科。

在工程力学中，对于杆件的受力分析和应力分布是非常重要的内容。

杆件是指在力的作用下只能沿着轴向伸缩的直细长构件，通常用来承受拉力或压力。

在本文中，我们将探讨杆件受力分析的方法以及应力分布的计算方式。

一、杆件受力分析在杆件受力分析中，主要考虑的是杆件所受的外力作用以及杆件内部所存在的支反力。

首先，我们需要明确杆件所受的外力有哪些类型。

常见的外力包括拉力、压力、剪力和扭矩等。

在分析杆件受力时，我们通常采用自由体图的方法，即将杆件与其它部分分开，将作用在该部分上的所有外力和内力用矢量图表示出来。

对于杆件受力分析，我们需要应用平衡条件，即受力平衡和力矩平衡条件。

受力平衡条件要求受力杆件在平衡状态下，合力为零，合力矩为零。

力矩平衡条件要求受力杆件在平衡状态下，合力矩为零。

通过应用这些平衡条件，我们可以得到杆件内部的支反力以及所受外力的大小和方向。

二、应力分布计算一旦我们确定了杆件所受的外力以及杆件内部的支反力，接下来我们需要计算杆件上的应力分布情况。

应力是指杆件某一截面上内部单位面积上所承受的力的大小。

常见的应力类型有拉应力、压应力和剪应力等。

在杆件内部，由于受力的存在，会导致杆件内部存在正应力和剪应力。

正应力是指作用在截面上的力沿截面法线方向的分量，而剪应力是指作用在截面上的力沿截面切线方向的分量。

根据杆件破坏的准则，我们通过计算截面上的应力分布来评估杆件的强度是否满足要求。

在计算杆件的应力分布时，一种常用的方法是应用梁弯曲理论。

根据梁弯曲理论，我们可以通过计算杆件的弯矩和截面形状来确定截面各点上的应力分布。

杆件的弯矩可以通过受力分析和力矩平衡条件来计算，而截面形状可以通过测量或者根据设计参数确定。

另外，我们还可以利用有限元分析方法来计算杆件的应力分布。

有限元分析是一种数值计算方法，通过将复杂的结构分解为许多小的单元，然后通过数值模拟的方式来计算每个单元上的应力分布。

工程力学3-力系的平衡条件和平衡方程

工程力学3-力系的平衡条件和平衡方程


例1 例1 求图示刚架的约束反力。
解：以刚架为研究对象，受力如图。
F x0:F A xq b0
P a A
q
b
F y0:F A yP0
P
MA(F)0:
MA
MAPa12q b2 0
FAx
A
FAy
q
解之得：
FAx qb
FAy P
MAPa 1 2qb 2
例2 例2 求图示梁的支座反力。
解：以梁为研究对象，受力如图。
坐标，则∑Fx＝0自然满足。于是平面 平行力系的平衡方程为：
O
F2
x
F y 0 ; M O ( F ) 0
平面平行力系的平衡方程也可表示为二矩式：
M A ( F ) 0 ; M B ( F ) 0
其中AB连线不能与各力的作用线平行。
[例5] 已知：塔式起重机 P=700kN, W=200kN (最大起重量)， 尺寸如图。求：①保证满载和空载时不致翻倒，平衡块
解： 1．分析受力
建立Oxy坐标系。 A处约束力分量为FAx和FAy ；钢 索的拉力为FTB。
解： 2．建立平衡方程
Fx＝0
MAF＝ 0
－ F Q 2 l－ F W xF T Blsi＝ n0
FTB＝ FPlxs＋ iF nQ2 l＝ 2FlWxFQ
FAx F TBco ＝ s0
Fy＝0
F A ＝ x 2 F W x l F Q l co＝ s3 3 F lW 0xF 2 Q
[例1] 已知压路机碾子重P=20kN, r=60cm, 欲拉过h=8cm的障碍物。 求：在中心作用的水平力F的大小和碾子对障碍物的压力。
解： ①选碾子为研究对象 ②取分离体画受力图
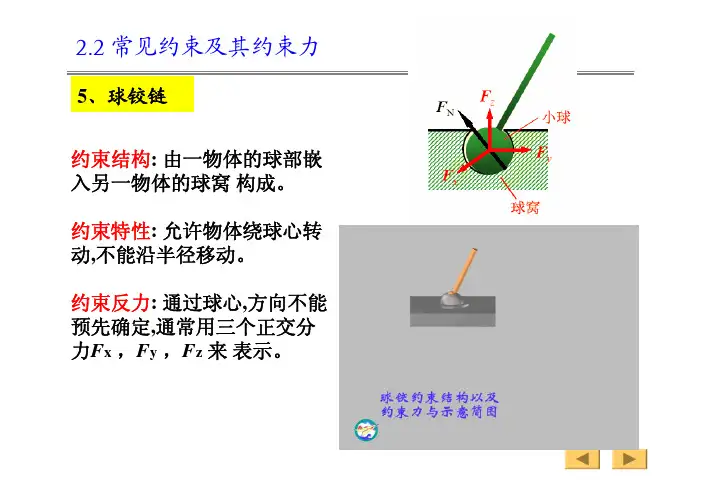
理论力学课件 受力分析与受力图、第三章

理论力学课件 受力分析与受力图、第三章

5、球铰链
约束结构: 由一物体的球部嵌入另一物体的球窝构成。

约束特性: 允许物体绕球心转动,不能沿半径移动。

约束反力: 通过球心,方向不能预先确定,通常用三个正交分力F x，F y，F z来表示。

人造髋关节
二力杆工程实例
固定端约束除了加约束力，还要加上约束力偶。

运动学角度：固定端既限制线位移，又限制角位移，如果只有约束力，则构件将转动。

必须有约束力偶才行。

力系简化角度：固定端所受的力是一个复杂的平面任意力系，力系向端部某点简化的结果是一力和一力偶。

CD是不是二力
杆？
2.3 受力分析与受力图
刚化原理：若变形体在某一力系作用下处于平衡，则将此变形体刚化为刚体，其平衡状态保持不变。

只有刚化原理没有软化原理。

1. 右拱BC 的受力图。

C
B
解：
F C
F B
2. 左拱AC 的受力图。

A C
F
F Ax C F
F Ay。

工程力学：第三章 空间问题的受力分析

工程力学：第三章 空间问题的受力分析


。CDB平面与水平
面间的夹角
，物重
。如起重杆的重量不计，试求
起重杆所受的压力和绳子的拉力。
解：取起重杆AB与 重物为研究对象。
取坐标轴如图所示。 由已知条件知：
列平衡方程 解得
§3-3 力对轴的矩 力F对z轴的矩就是分力Fxy 对点O的矩， 即
力对轴的矩是力使刚体绕该 轴转动效果的度量、是一个 代数量。
空间力偶系平衡的必要和充分条件是：该力偶系的合力偶矩等 于零，亦即所有力偶矩矢的矢量和等于零，即
由上式，有 欲使上式成立，必须同时满足
空间力偶系未知量）
空间力偶系平衡的必要和充分条件为：该力偶系中所有各力偶 矩矢在三个坐标轴上投影的代数和分别等于零。
§3-5 空间任意力系的平衡方程
可将上述条件写成空间任意力系的平衡方程
注：1.与平面力系相同，空间力系的平衡方程也有其它的形式。 2.六个独立的平衡方程，求解六个未知量。 3.可以从空间任意力系的普遍平衡规律中导出特殊情况的 平衡规律，例如空间平行力系、空间汇交力系和平面任意 力系等平衡方程。
例：设物体受一空间平行力系作用。 令z轴与这些力平行，则
绝对值： 该力在垂直于该轴的平面上的投影对于 这个平面与该轴的交点的矩的大小。
正负号： 从z轴正端来看，若力的这个投影使物体绕该轴 按逆时针转向转动，则取正号，反之取负号。
也可按右手螺旋规则来确定其正负号，如图所 示，姆指指向与z轴一致为正，反之为负。
当力与轴在同一平面时，力对该轴的矩等于零：
(1)当力与轴相交时 (此时h＝0)；
（三个方程，可 求解三个未知量）
空间汇交力系平衡的必要和充分条件为：该力系中所有各力 在三个坐标轴上的投影的代数和分别等于零。
工程力学第三章-力系的平衡

工程力学第三章-力系的平衡


将上式两边向x、y、z 轴投影，可得平衡方程
F F F
可以求解3个未知量。
x y
z
0 0 0
• 2.平面汇交力系
力系的平衡
• 力偶系的平衡方程 • 1.空间力偶系
平衡的充要条件（几何条件） M Mi 0 将上式两边向x、y、z 轴投影，可得平衡方程
M M M
可以求解3个未知量。
ix iy iz
0 0 0
• 2.平面力偶系
力系的平衡
• 平衡的充要条件:力偶系中各力偶矩的代数和等于零.
m 0
i
• 任意力系的平衡方程 空间任意力系： • 平衡的充要条件:力系的主矢和对任一点的主矩均为零。
FR 0
MO 0
G3 a
e
G 3(a b) FNAb G1e G 2L 0 G 3(a b) G1e G 2L FNA 2 b
由(1)、(2)式 得：
G1 G2 L
G1e G 2L G3 ab
3
A FN A b
B FN B
(2)空载时
不翻倒条件：FNB≥0 (4) 由 mA 0 得：
FAB = 45 kN
600
y B TBC 15 15 30 TBD
0 0 0
x
C
D
150
B
300
TBD=G E
A
E
FAB G
解题技巧及说明：
1、一般地，对于只受三个力作用的物体，且角度特殊时用 几 何法（解力三角形）比较简便。 2、一般对于受多个力作用的物体，且角度不特殊或特殊， 都用解析法。 3、投影轴常选择与未知力垂直，最好使每个方程中只有一 个未知数。
大学物理 力学-受力分析

大学物理 力学-受力分析

1
绪论
工程力学是一门理论性较强的技术基础课，它是诸多力学课 程的基础，并在工程技术领域中有着广泛的应用。
工程力学主要研究物体的机械运动和杆件弹性变形的一般规 律。它是高等工科院校的一门理论性较强的技术基础课程，为后 续课程的学习和解决工程实际问题提供力学的基本理论和方法。
机械设备或工程结构都是由若干构件组成的。当它们传递 运动或承受载荷时，各个构件都要受到力的作用。因此，首先必 须确定有哪些力在作用各个构件上，以及它们的大小和方向；其 次还必须为构件选用合适的材料，确定合理的截面形状和尺寸， 以保证构件既能安全可靠的工作又符合经济要求。这些都是工程 力学所要解决的问题。
26
总结
（1）光滑面约束——法向约束力 FN
（2）柔索约束——张力 FT
（3）光滑铰链——
r FAy
,
r FAx
（4）滚动支座—— F⊥N 光滑面
球铰链——空间三正交分力
止推轴承——空间三正交分力
27
§1.3 物体的受力分析与受力图
一、受力分析
在工程实际中，为了求出未知的约束反力，需要根据已 知力，应用平衡条件求解。为此，首先要确定构件受了几个 力，每个力的作用位置和作用方向，这种分析过程称为物体 的受力分析。
作用在物体上的力有：一类是主动力，如重力、风力、 气体压力等。二类是约束反力，为未知的被动力。
注意，凡图中未画出重力的就是不计重力，凡不提及摩 擦时视为光滑。
28
二、受力图
画物体受力图主要步骤为： ①选研究对象；② 取分离体； ③画上主动力；④画出约束反力。 [例1] 画出图示碾子的受力图。 解：画出简图 画出主动力 画出约束反力
1. 由柔软的绳索、链条或皮带构成的约束 绳索类只能受拉，所以它们的约束反力是作用在接触点，
《工程力学第三章》PPT课件

《工程力学第三章》PPT课件

F A y － F Q － F W ＋ F T B sin＝ 0
FA＝ y － l－ l xFW＋F2Q
h
15
平面力系的平衡条件与平衡方程
平面一般力系的平衡条件与平衡方程－例题 1
FTB＝FWlxs＋ iF nQ2l＝2FlWxFQ
解： 3．讨论 由结果可以看出，当x＝l，即电动机移动到吊车大梁 右端B点处时，钢索所受拉力最大。钢索拉力最大值为
因此，力系平衡的必要与充分条件是力系的主矢和对任意一 点的主矩同时等于零。这一条件简称为平衡条件
满足平衡条件的力系称为平衡力系。 本章主要介绍构件在平面力系作用下的平衡问题。
h
8
平面力系的平衡条件与平衡方程
平面一般力系的平衡条件与平衡方程
对于平面力系，根据第2章中所得到的主矢和主矩 的表达式，力系的平衡条件可以写成
吊 车 大 梁 AB 上 既 有 未 知 的 A 处 约 束力和钢索的拉力，又作用有已知的 电动机和重物的重力以及大梁的重力。 所以选择吊车大梁AB作为研究对象。 将吊车大梁从吊车中隔离出来。
h
12
平面力系的平衡条件与平衡方程
平面一般力系的平衡条件与平衡方程－例题 1
解： 1．分析受力
建立Oxy坐标系。 A处约束力分量为FAx和FAy ；钢 索的拉力为FTB。
平面一般力系的平衡条件与平衡方程－例题 1
解： 2．建立平衡方程
Fx＝0
MAF＝ 0
－ F Q2 l－ F W xF T Blsi＝ n0
FTB＝FWlxs＋ inFQ2l＝2FlWxFQ
FAxFTBco＝ s0
Fy＝0
F A＝ x 2F W x lF Q l co＝ s3 3 0 F lW xF 2 Q
工程力学受力分析课件

工程力学受力分析课件


02
受力分析基础
力的定义与分类
定义
力是物体之间的相互作用，是改 变物体运动状态的原因。
分类
根据力的作用效果，力可以分为 拉力、压力、剪切力、扭转力等 。根据力的性质，力可以分为重 力、弹性力、摩擦力等。
静力与动力
静力
物体在力的作用下处于平衡状态，即 合外力为零。静力分析主要用于研究 物体的平衡状态和受力情况。
轴的受力分析
转轴的受力分析 转轴的约束条件 转轴的内力和变形
轴的受力分析
转轴的强度和刚度要求 传动轴的受力分析 传动轴的约束条件
轴的受力分析
传动轴的内力和变形
传动轴的强度和刚度要求
轮轴的受力分析
车轮与车轴的连接受力分析 车轮与车轴的连接方式 车轮与车轴的内力和变形
轮轴的受力分析
车轮与车轴的强度和刚度要求 齿轮传动轮轴的受力分析 齿轮传动的特点和应用
详细描述
1. 机器设计：机械系 统的设计过程中，精 确的受力分析是关键 ，通过分析可以优化 机器的结构设计，提 高机器的承载能力和 使用寿命。
2. 零部件优化：针对 关键零部件，受力分 析可以帮助优化其形 状、尺寸和材料选择 ，提高其性能并降低 成本。
3. 动态性能：对于高 速运转的机器，受力 分析需考虑动态载荷 ，以确保机器在各种 工况下的稳定性和可 靠性。
1. 结构设计：建筑结构设计中， 需要精确分析各种受力情况，如 重力、风载、地震载荷等，以确 保建筑的安全性和稳定性。
3. 材料选择与优化：根据受力分 析结果，可以选择合适的材料和 优化结构设计，以降低成本并提 高效率。
机械系统中的受力分析案例
总结词：机械系统中 ，工程力学受力分析 有助于优化机器设计 ，提高机器性能与使 用寿命。
《工程力学》第三章精选习题及解答提示

《工程力学》第三章精选习题及解答提示

《工程力学》第三章精选习题及解答提示3—1 图示空间三力5001=F N ，10002=F N ，7003=F N ，求此三力在x ，y ，z 轴上的投影；并写出三力矢量表达式。

【解】（1）求三力在x ，y ，z 轴上的投影。

力1F的投影： ⎪⎪⎪⎩⎪⎪⎪⎨⎧=⨯=+⨯==⨯=+⨯-=N 224515002110N 447525002122211112211F F y xoz F F F F z y x 轴垂直）坐标面内，与位于—（———＝－－ 力2F 的投影（采用二次投影法）：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⨯=++⨯=-=⨯-=+⨯+++⨯-=⨯=+⨯+++⨯-=N 26714110003211N 802143100032132132N 53514210003223213222222222222222222222222F F F F F F z y x ＝－－ 力3F 的投影（3F 位于xoy 坐标面内，与x 轴平行同向）：⎪⎩⎪⎨⎧====00N 7003333z y x F F F F（2）写出三力的矢量表达式： k i k F j F i F F z y x ⋅+⋅-=⋅+⋅+⋅=2244471111 k j i k F j F i F F z y x ⋅+⋅-⋅-=⋅+⋅+⋅=2678025352222 i k F j F i F F z y x ⋅=⋅+⋅+⋅=7003333 3—2 半径为r 的斜齿轮，其上作用有力F ，如图所示。

已知角α和角β，求力F 沿坐标轴的投影及力F 对y 轴之矩。

【解】（1）求力在坐标轴的投影。

根据图中所示的力F 的位置关系，可知本题宜采用二次投影法：⎪⎩⎪⎨⎧⋅-=⋅⋅-=⋅⋅=αβαβαsin cos cos sin cos F F F F F F z y x（2）求力F 对y 轴之矩： 由图可知，力F 可分解为三个分力，分别是：轴向力a F ；径向力r F ；圆周力t F ，即： t r a F F F F ++=由合力矩定理得：βαβαsin cos sin cos 00)()()()(⋅⋅⋅=⋅⋅⋅++=++=r F r F F m F m F m F m t y r y a y y 3—3 铅垂力500=F N ，作用于曲柄上，如图所示，求该力对于各坐标轴之矩。

工程力学第三章 受力分析


F
D
C
F C
A
FA
F
FAx A FAy
精品课表件示法二
C
F C
23
例题2
A
如图所示，重物重G = 20 kN,用
60
D
B
钢丝绳挂在支架的滑轮B上，钢丝 绳的另一端绕在铰车D上。杆AB与
BC铰接，并以铰链A，C与墙连接。
30
如两杆与滑轮的自重不计并忽略摩
G
擦 和 滑 轮 的 大 小 ， 试 画 出 杆 AB 和
A
F
H
D
E
B
C
F
A
H
FB
D B
FC
E C
精品课件
12
[例5] 画出下列各构件的受力图
O
C
E
DQLeabharlann AB精品课件
13
O
C
E
D
Q
A
B
Ncx Ncy
NBx NBy
精品课件
N’cy
N’cx
14
[例6] 画出下列各构件的受力图
精品课件
15
尖点问题
应去掉约束
精品课件
应去掉约束
16
[例7] 画出下列各构件的受力图
梯子放在光滑水平面上，
若其自重不计，但在AB的 中点处作用一铅直载荷F。 试分别画出梯子的AB，AC
部分以及整个系统的受力
图。
精品课件
10
F
H D B
解： 1.梯子AB 部分的受力图。
FAy
A
FA
FAx
H
E
FB
FD
D
C B
2.梯子AC 部分的受力图。

工程力学课后习题标准答案静力学基本概念与物体受力分析标准答案

第一章静力学基本概念与物体的受力分析下列习题中，未画出重力的各物体的自重不计，所有接触面均为光滑接触。

1.1试画出下列各物体（不包括销钉与支座）的受力图。

解：如图1.2画出下列各物体系统中各物体（不包括销钉与支座）以及物体系统整体受力图。

解：如图1.3铰链支架由两根杆AB、CD和滑轮、绳索等组成，如题1.3图所示。

在定滑轮上吊有重为W的物体H。

试分别画出定滑轮、杆CD、杆AB和整个支架的受力图。

解：如图1.4题1.4图示齿轮传动系统，O1为主动轮，旋转方向如图所示。

试分别画出两齿轮的受力图。

解：1.5结构如题1.5图所示，试画出各个部分的受力图。

解：第二章汇交力系2.1在刚体的A点作用有四个平面汇交力。

其中F1＝2kN，F2=3kN，F3=lkN，F4=2.5kN，方向如题2.1图所示。

用解读法求该力系的合成结果。

解2.2 题2.2图所示固定环受三条绳的作用，已知F1＝1kN，F2=2kN，F3=l.5kN。

求该力系的合成结果。

解：2.2图示可简化为如右图所示2.3 力系如题2.3图所示。

已知：F 1＝100N ，F 2=50N ，F 3=50N ，求力系的合力。

解：2.3图示可简化为如右图所示2.4 球重为W ＝100N ，悬挂于绳上，并与光滑墙相接触，如题2.4图所示。

已知，试求绳所受的拉力及墙所受的压力。

解：2.4图示可简化为如右图所示墙所受的压力F=57.74N2.5 均质杆AB 重为W 、长为 l ，两端置于相互垂直的两光滑斜面上，如题2.5图所示。

己知一斜面与水平成角，求平衡时杆与水平所成的角及距离OA 。

解：取 AB 杆为研究对象，受力如图所示由于杆件再三力作用下保持平衡，故三力应汇交于C 点。

AB 杆为均质杆，重力作用在杆的中点，则W 作用线为矩形ACBO 的对角线。

由几何关系得 所以 又因为 所以2.6 一重物重为20kN ，用不可伸长的柔索AB 及BC悬挂于题2.6图所示的平衡位置。

第3章 平面静定结构受力分析(17)

第三章平面静定结构受力分析静定结构受力分析之歌内力分析要提升，等效截面法冲锋。

内力标记有新规，杆段截面都分明。

剪力轴力与前无异，弯矩顺时针恒正。

受力图上力已知，叠加绘图分分钟。

一、基本概念和公式1．任意截面x 的内力分量的求法。

图3-1截面x 上的内力分量表示段x 截面(a)(b)2q(c)32qa /2qa /-2e M qa =Cx F qa=Ax F qa=-AB C对于如题图3-1所示的平面力系，平衡截面法可表为N,,,Q,,,()()xA i x i xAxxCxA i y i yAxxCxA C i C i AxxCF F F F F F M M F M F =-==-==-=∑∑∑∑∑∑（3-1）N,,,Q,,,()()xC i x i xxCxAxC i y i yxCxAxC C i C i xCxAF F F F F F M M F M F =-==-==-=∑∑∑∑∑∑（3-2）式（3-1）中的第一个等式表明：Ax 段x 截面的内力分量等于本段上外力在相应方向上投影（或力矩）的代数和的负值—平衡截面法，第二个等式表明：Ax 段x 截面的内力分量等于另段xC 上的外力在相应方向上投影（或力矩）的代数和—等效截面法。

式（3-2）第一个等式表明：xC 段x 截面的内力分量等于本段上外力在相应方向上投影（或关于截面形心C 的力矩）的代数和的负值—平衡截面法，第二个等式表明：xC 段x 截面的内力分量等于另段Ax 上的外力在相应方向上投影（或力矩）的代数和—等效截面法。

式（3-1）的第二个等式更深刻和具体的表述为：Ax 段x 截面的内力的主矢和主矩等于xC 段上所有外力关于x 截面形心的主矢和主矩。

用内力分量表示就是：（1）Ax 段x 截面的轴力N,xA F 等于xC 段上所有外力在轴线方向投影的代数和；（2）剪力Q,xA F 等于xC 段上所有外力在竖直方向投影的代数和；（3）弯矩xA M 等于xC 段上所有外力关于x 截面形心的力矩的代数和。

工程力学中的杆件受力分析

工程力学中的杆件受力分析杆件在工程力学中是常见的结构元件，广泛应用于各种工程领域。

在设计和施工过程中，了解杆件受力分析原理和方法对于确保结构的安全和稳定至关重要。

本文将介绍工程力学中的杆件受力分析，包括受力原理、受力分析方法等内容。

一、受力原理在工程力学中，杆件受力分析的基础是牛顿第三定律，即作用力与反作用力相等，方向相反。

杆件受力可以分为两类：拉力和压力。

拉力是指杆件被拉伸的力，产生拉力的力又称为拉力的作用力；压力是指杆件被压缩的力，产生压力的力又称为压力的作用力。

根据受力原理，杆件上任意一点的受力可以通过平衡方程进行分析。

二、杆件受力分析方法1. 自由体图法自由体图法是杆件受力分析中常用的方法之一。

其基本思想是将杆件从整体中分离出来，将受力点周围的力及其作用方向用箭头表示在杆件上，然后根据受力平衡条件进行分析。

通过自由体图法可以清晰地了解杆件上各点的受力情况，从而判断杆件的受力状态。

2. 三力平衡法三力平衡法适用于已知杆件两端作用力和一个内力时的受力分析问题。

通过将杆件切割成两个自由体，并根据平衡条件求解未知内力的大小和方向。

三力平衡法常用于悬臂梁和简支梁等结构的受力分析。

3. 应力分析法应力分析法是一种通过分析杆件内部的应力情况，进而推导出受力的方法。

根据杆件材料的本构关系，可以得到应力与应变的关系，进而得到受力的大小和方向。

应力分析法适用于解决杆件受力分布不均匀或非轴对称的情况。

三、实例分析下面通过一个实例来说明杆件受力分析的具体过程。

例：一根长度为L、截面积为A的圆柱形杆件，其一端固定在墙壁上，另一端悬挂一个质量为m的物体。

假设杆件重力忽略不计，求解悬挂物体对杆件的拉力。

解：首先，根据题设，可以确定杆件受力的情况是纯拉力。

由牛顿第三定律可知，悬挂物体对杆件的拉力大小等于杆件对悬挂物体的拉力大小且方向相反。

其次，将杆件切割成两个自由体：杆件部分和悬挂物体部分。

以杆件部分为自由体进行受力分析。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3
二、受力分析的步骤 取研究对象； ① 取研究对象； 取分离体； ② 取分离体； 画上主动力； ③ 画上主动力； 找接触点或连接点； ④ 找接触点或连接点； 画出约束反力。 ⑤ 画出约束反力。
4
例1 画出图中的球和杆AB的受力分析图
解： B B SBC N2 P N1 A 600 C P N2 A XA YA
D
FA
8. 整体的受力图。
D A
A
θ
K C B Ⅰ
θ
K C B Ⅰ E
FEy FA FCy FCx
C
F′ K
FEx
F′ BD B Ⅰ
Ⅱ
E
Ⅱ
A
θ
P
P
Ⅱ
9. 杆AB，滑轮Ⅰ，Ⅱ 以及重物、 钢绳（包括销钉B）一起的受力图。
P
37
例 题8
重为P 的重物悬挂在滑轮支
C
架系统上，如图所示。设滑轮 的中心B与支架ABC相连接，AB
A C D B B
7
解： 1. 杆 BC 的受力图。
B B D
FB
B
F
A C
C
FC
8
2. 杆AB 的受力图。 正交分解
B B D
三力平衡汇交 FB
B B
FB
F
A C
F FAy
A
D D
F
A
H
FAx
FA
第二种画法
9
第一种画法
例
4
F
H D B
A
E C
如图所示，梯子的两部分 AB和AC在A点铰接，又在 D ，E两点用水平绳连接。 梯子放在光滑水平面上， 若其自重不计，但在AB的 中点处作用一铅直载荷F。 试分别画出梯子的AB，AC 部分以及整个系统的受力 图。
20
物体的受力分析 物体的受力分析
P
F
C
如图所示的三铰拱 桥 ， 由左右两拱桥铰接 而成。 设各拱桥的自重 而成 。 不计， 不计 ， 在拱上作用有载 荷F，试分别画出左拱 和右拱的受力图。 和右拱的受力图。
A
B
21
解：
1. 右拱 BC 的受力图。 的受力图。
F
P
C
A
B
FC
C
B
FB
22
2. 左拱 AC 的受力图。 的受力图。
2
§1-4 物体的受力分析和受力图 一、受力分析 无论是研究物体的平衡还是研究物体的运动规律， 无论是研究物体的平衡还是研究物体的运动规律， 都需要分析物体的受力情况。 都需要分析物体的受力情况。 1.分离体（研究对象） 1.分离体（研究对象） 分离体 2.受力分析 2.受力分析 3.受力图 3.受力图 作用在物体上的力有：主动力,被动力(约束反力) 作用在物体上的力有：主动力,被动力(约束反力)。
33
解：
1. 杆BD（B处为没有销钉的孔）的受力图。 FDB
D A D
θ
K C B Ⅰ
2. 杆AB（B处仍为没 有销钉的孔）的受力图。
B
E
Ⅱ FA
A
FCy FBx FCx C FBy
B
FBD
P
34
D
F′ DB
3. 杆DE的受力图。
D A
K
FK
F′ Cx
B Ⅰ
C
θ
K
F′y C
FB1y
F′ K
B
C
FB1x
10
解：
1.梯子AB 部分的受力图。 FAy
F
H D B
A
F
H E C
A
FAx
′ FAx
F′ D
A
FB
D B
′ FAy
F′ E
E
FC
2.梯子AC 部分的受力图。
C
11
3.梯子整体的受力图。
F
H D B
A
F
H E C
A
FB
D B E
FC
C
12
[例5] 画出下列各构件的受力图
O
C
E Q D A B
13
O
C
E Q D A B
Ncx Ncy
N’cy N’cx NBx
14
NBy
[例6] 画出下列各构件的受力图 ]
15
尖点问题
应去掉约束
应去掉约束
16
[例7] 画出下列各构件的受力图
17
三、画受力图应注意的问题
1、不要漏画力 、 除主动力外，只要物体相互接触，就一定存 除主动力外，只要物体相互接触， 在有机械作用。要分清研究对象（受力体） 在有机械作用。要分清研究对象（受力体） 都与周围哪些物体（施力体）相接触， 都与周围哪些物体（施力体）相接触，接触 处必有力，力的方向由约束类型而定。 处必有力，力的方向由约束类型而定。
要注意力是物体之间的相互机械作用。因此对 要注意力是物体之间的相互机械作用。 2、不要多画力 、 于受力体所受的每一个力， 于受力体所受的每一个力，都应能明确地指出 它是哪一个施力体施加的。 它是哪一个施力体施加的。
18
3、不要画错力的方向 、 约束反力的方向必须严格地按照约束的类型来画， 约束反力的方向必须严格地按照约束的类型来画，不 能单凭直观或根据主动力的方向来简单推想。 能单凭直观或根据主动力的方向来简单推想。在分析 两物体之间的作用力与反作用力时，要注意， 两物体之间的作用力与反作用力时，要注意，作用力 的方向一旦确定，反作用力的方向一定要与之相反， 的方向一旦确定，反作用力的方向一定要与之相反， 不要把箭头方向画错。 不要把箭头方向画错。 4、受力图上不能再带约束。 、受力图上不能再带约束。 即受力图一定要画在分离体上。 即受力图一定要画在分离体上。
P1 A F E D B H C G
θ
P2
29
例 题4
解：
1.物块 B 的受力图。
FE
FD D B
2. 球A 的受力图。
A F H C E A F P1 D B P1 G
E I H FH FF FC
P2
G C FG
θ
P2
3.滑轮 C 的受力图。 30
例 题 6
如图所示压榨机中，杆AB
E D
和BC的长度相等，自重忽略 不计。A ，B，C ，E处为铰 链连接。已知活塞D上受到油
A
P B
27
例 题3 解：
碾子的受力图为: F F
A
P B
P A FNA B FNB
28
例 题4
在图示的平面系统中，匀质 球A 重P1，本身重量和摩擦不计 的理想滑轮C 和柔绳维持在仰角 是θ 的光滑斜面上，绳的一端挂 着重P2 的物块B。试分析物块B , 球A和滑轮C的受力情况，并分 别画出平衡时各物体的受力图。
Ⅰ
FEy F Ex
E
E
Ⅱ
F′ 1
P
4. 轮Ⅰ (B处为没有销钉的孔）的受力图。
35
5. 轮Ⅱ的受力图。
FB F1 Ⅱ
D A
6. 销钉B的受力图。
F′ BD
F′ By
B
F′ x B1
′ FB1y
F′ Bx
F2
B Ⅰ
θ
K C
F′ K
F′ By
F′ B
F′ BD
B
F′ Bx
E
Ⅱ
F′ B
P
F′ 1
7. 销钉B与滑轮Ⅰ 一起的受力图。 36
画约束反力时， 画约束反力时，一定要按照约束的固有性质画 5 切不可主观臆断！ 图，切不可主观臆断！
画出图中球O与杆 与杆AB的受力分析图 例2 画出图中球 与杆 的受力分析图
6
例 3
等腰三角形构架ABC 的顶点 A，B，C 都用铰链连接，底边 AC固定，而AB 边的中点D 作用 有平行于固定边AC 的力F，如图 所示。不计各杆自重，试画出杆 AB 和BC 的受力图。 F
30o
接 。 如两杆与滑轮的自重不计并忽
G
略摩擦和滑轮的大小，试画出杆AB 略摩擦和滑轮的大小， 试画出杆 以及滑轮 的受力图。 和BC以及滑轮 的受力图。 以及滑轮B的受力图
24
C
A D
60o
解： 1.杆AB的受力图。 1.杆AB的受力图 的受力图。
B
FAB
A B
2.杆 2.杆BC 的受力图。 的受力图。
39
P
FBC
5. 轮 D 的受力图。 4. 销钉 B 的受力图。
F′ BC
F′ BA
H A
45o
FTE
FTD
D
C
F′ By
B
E
F′ Bx
P
FTB
B F
FTI
45o
I
E
D
6. 轮 I 的受力图。
FPx
I
FPy
P
40
• 作业：
41
B
缸内的总压力为F 。试画出
θ
C
A
θ
杆AB ，活塞和连杆以及压块 C的受力图。
31
解：
1.杆AB的受力图。 2. 活塞和连杆的受力图。
E D A
B
F BA
F
FA
B A
3. 压块 C 的受力图。
θCBiblioteka θθFCB FAB C F Cx
B
θ
FBC
θ
FCy
32
例 题 7
D A
θ
K C B Ⅰ
E
Ⅱ
P
如图所示平面构架，由杆AB ， DE及DB铰接而成。钢绳一端拴 在K处，另一端绕过定滑轮Ⅰ和 动滑轮Ⅱ后拴在销钉B上。重物 的重量为P，各杆和滑轮的自重 不计。（1）试分别画出各杆， 各滑轮，销钉B以及整个系统的 受力图；（2）画出销钉B与滑轮 Ⅰ一起的受力图；（3）画出杆 AB ，滑轮Ⅰ ，Ⅱ ，钢绳和重物 作为一个系统时的受力图