最新工程力学第三章受力分析

工程力学教程第4版第3章思考题答案_副本问题1问题描述：请说明受力分析方法的基本原理，并说明在实际工程中使用受力分析的步骤。

答案：受力分析是工程力学中常用的一种方法，用于分析物体所受的力和力的作用方向，以及这些力对物体的影响。

受力分析的基本原理是根据牛顿第二定律，即物体所受的合力等于物体的质量乘以加速度，通过受力分析可以求解物体在受力作用下的运动情况。

在实际工程中，使用受力分析的步骤如下：1.确定受力的作用方向和大小。

根据问题描述和已知条件，确定受力的作用方向和大小。

可使用向量图形表示受力的方向和大小。

2.绘制受力图。

根据受力的作用方向和大小，在纸上绘制受力图。

受力图可以使用箭头表示力的方向和长度表示力的大小。

3.分解力和合力。

根据受力图，可以将受力分解为多个力的合力。

将合力分解为多个力可以使计算更加简单，并且可以更好地理解力的作用。

4.应用牛顿第二定律求解受力的影响。

根据受力的作用方向和大小，使用牛顿第二定律求解受力的影响。

根据物体的质量和加速度，可以计算物体所受的合力。

使用受力分析可以解决物体的运动问题。

5.检查和验证结果。

在完成受力分析后，应对所得结果进行检查和验证。

可以使用其他方法验证受力分析的结果。

通过以上步骤，可以应用受力分析方法解决实际工程中的问题，该方法可以用于求解任何物体的运动情况。

问题2问题描述：请说明轴力和切力的概念，并分别给出它们的计算公式。

答案：轴力和切力是力学中的两个重要概念，用于描述杆件或梁的受力情况。

轴力是指垂直于横截面的力，也可以理解为沿着杆件轴线的力。

轴力的计算公式为：N = A·σ其中，N表示轴力，A表示横截面积，σ表示单位面积上的轴向应力。

切力是指垂直于杆件轴线的力，作用在杆件截面上的力。

切力的计算公式为：Q = A·τ其中，Q表示切力，A表示横截面积，τ表示单位面积上的切应力。

轴力和切力是杆件或梁内力的两个分量，通过计算轴力和切力可以确定杆件或梁在受力状态下的内力分布情况。

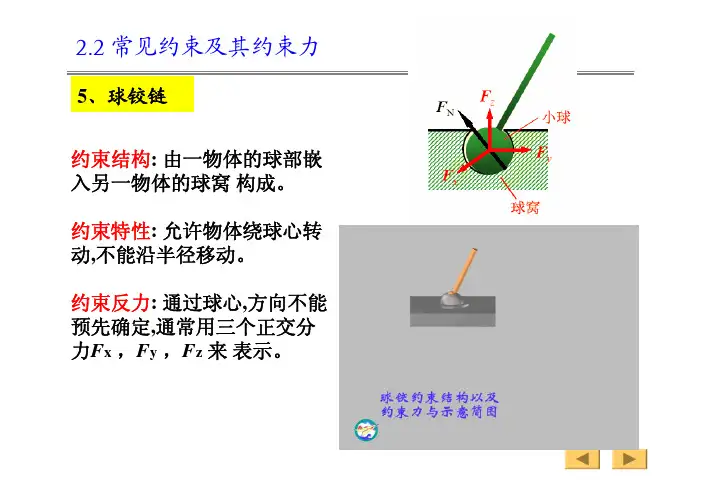
5、球铰链
约束结构: 由一物体的球部嵌入另一物体的球窝构成。

约束特性: 允许物体绕球心转动,不能沿半径移动。

约束反力: 通过球心,方向不能预先确定,通常用三个正交分力F x，F y，F z来表示。

人造髋关节
二力杆工程实例
固定端约束除了加约束力，还要加上约束力偶。

运动学角度：固定端既限制线位移，又限制角位移，如果只有约束力，则构件将转动。

必须有约束力偶才行。

力系简化角度：固定端所受的力是一个复杂的平面任意力系，力系向端部某点简化的结果是一力和一力偶。

CD是不是二力
杆？
2.3 受力分析与受力图
刚化原理：若变形体在某一力系作用下处于平衡，则将此变形体刚化为刚体，其平衡状态保持不变。

只有刚化原理没有软化原理。

1. 右拱BC 的受力图。

C
B
解：
F C
F B
2. 左拱AC 的受力图。

A C
F
F Ax C F
F Ay。

1第三章力系的平衡§3–1 平面力系的平衡方程§3–2 空间力系的平衡方程§3–3 物体系统的平衡方程§3–4 静定与静不定的基本概念§3-1 平面力系的平衡方程由于=0 为力平衡M O =0 为力偶也平衡所以平面任意力系平衡的充要条件为：力系的主矢F R 和主矩M O 都等于零，即：)()(22=+=∑∑Y X F R 0)(==∑i O O F m M 1、平面任意力系的平衡方程R F=∑X 0)(=∑i A F m 0)(=∑i B F m ②二矩式条件：x 轴不AB连线⊥0)(=∑i A F m 0)(=∑i B F m 0)(=∑i C F m ③三矩式条件：A ,B ,C 不在同一直线上上式有三个独立方程，只能求出三个未知数。

=∑X 0=∑Y 0)(=∑i O F m ①一矩式①平面汇交力系=∑xF 0=∑yF2、平面特殊力系的平衡方程②平面力偶系=∑M ③平面平行力系=∑y F 0)(=∑F M O 0)(=∑F MB0)(=∑F M A AB 不x 轴⊥[例] 已知：P , a , 求：A 、B 两点的支座反力？解：①选AB 梁研究②画受力图（以后注明解除约束，可把支反力直接画在整体结构的原图上）)(=∑i A F m 由32 ,032PN a N a P B B =∴=⋅+⋅-0=∑X 0=A X 0=∑Y 3,0PY P N Y A B B =∴=-+解除约束,0==∑A X X 由022;0)(=⋅-+⋅⋅+⋅=∑a P m aa q a R F m B A 0=∑Y 0=--+∴P qa R Y B A )kN (122028.01628.02022=⨯+-⨯-=+--=P a m qa R B )kN (24128.02020=-⨯+=-+=B A R qa P Y [例] 已知：P =20kN, m =16kN·m, q =20kN/m, a =0.8m求：A 、B 的支反力。

《工程力学》第三章精选习题及解答提示3—1 图示空间三力5001=F N ，10002=F N ，7003=F N ，求此三力在x ，y ，z 轴上的投影；并写出三力矢量表达式。

【解】（1）求三力在x ，y ，z 轴上的投影。

力1F的投影： ⎪⎪⎪⎩⎪⎪⎪⎨⎧=⨯=+⨯==⨯=+⨯-=N 224515002110N 447525002122211112211F F y xoz F F F F z y x 轴垂直）坐标面内，与位于—（———＝－－ 力2F 的投影（采用二次投影法）：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⨯=++⨯=-=⨯-=+⨯+++⨯-=⨯=+⨯+++⨯-=N 26714110003211N 802143100032132132N 53514210003223213222222222222222222222222F F F F F F z y x ＝－－ 力3F 的投影（3F 位于xoy 坐标面内，与x 轴平行同向）：⎪⎩⎪⎨⎧====00N 7003333z y x F F F F（2）写出三力的矢量表达式： k i k F j F i F F z y x ⋅+⋅-=⋅+⋅+⋅=2244471111 k j i k F j F i F F z y x ⋅+⋅-⋅-=⋅+⋅+⋅=2678025352222 i k F j F i F F z y x ⋅=⋅+⋅+⋅=7003333 3—2 半径为r 的斜齿轮，其上作用有力F ，如图所示。

已知角α和角β，求力F 沿坐标轴的投影及力F 对y 轴之矩。

【解】（1）求力在坐标轴的投影。

根据图中所示的力F 的位置关系，可知本题宜采用二次投影法：⎪⎩⎪⎨⎧⋅-=⋅⋅-=⋅⋅=αβαβαsin cos cos sin cos F F F F F F z y x（2）求力F 对y 轴之矩： 由图可知，力F 可分解为三个分力，分别是：轴向力a F ；径向力r F ；圆周力t F ，即： t r a F F F F ++=由合力矩定理得：βαβαsin cos sin cos 00)()()()(⋅⋅⋅=⋅⋅⋅++=++=r F r F F m F m F m F m t y r y a y y 3—3 铅垂力500=F N ，作用于曲柄上，如图所示，求该力对于各坐标轴之矩。