传递函数

传递函数概念
在数学中，函数是一种关系，将一个集合的每个元素（输入）映
射到另一个集合的唯一元素（输出）。

传递函数就是在这种映射关系
中的一种特殊情况，指的是当一个元素作为一个函数的输入时，该函
数的输出可以作为另一个函数的输入。

也就是说，如果存在两个函数f 和g，当f(x)的输出作为g的输入时，g(f(x))的输出与g(x)的输出相等，那么函数g被称为f的传递函数。

反过来，如果函数f是g的传
递函数，则我们也可以称g为f的逆传递函数。

传递函数在数学、物理、计算机科学等领域中都有广泛的应用。

在数学和物理中，传递函数可以用来描述信号、电路等物理系统的行为。

在计算机科学中，传递函数可以用来优化计算机程序的执行速度。

此外，在控制论、信号处理、通信等领域中，传递函数也是不可或缺
的概念。

总之，传递函数是一种重要的数学概念，在实际应用中具有广泛
的应用价值。

通过研究传递函数，我们可以进一步理解复杂的物理系统、计算机程序等，并为实际问题提供更好的解决方案。

2-6 传递函数求解控制系统的微分方程，可以得到在确定的初始条件及外作用下系统输出响应的表达式，并可画出时间响应曲线，因而可直观地反映出系统的动态过程。

如果系统的参数发生变化，则微分方程及其解均会随之而变。

为了分析参数的变化对系统输出响应的影响，就需要进行多次重复的计算。

微分方程的阶次愈高，这种计算愈复杂。

因此，仅仅从系统分析的角度来看，就会发现采用微分方程这种数学模型，当系统阶次较高时，是相当不方便的。

以后将会看到，对于系统的综合校正及设计，采用微分方程这一种数学模型将会遇到更大的困难。

目前在经典控制理论中广泛使用的分析设计方法——频率法和根轨迹法，不是直接求解微分方程，而是采用与微分方程有关的另一种数学模型——传递函数，间接地分析系统结构参数对响应的影响。

所以传递函数是一个极其重要的基本概念。

一、传递函数的概念及定义在[例2-7]中，曾建立了RC 网络微分方程，并用拉氏变换法对微分方程进行了求解。

其微分方程（2-44）为)()(t u t u dtdu RC r c c =+ 假定初始值0)0(=c u ，对微分方程进行拉氏变换，则有)()()1(s U s U RCs r c =+网络输出的拉氏变换式为)(11)(s U RCs s U r c += （2-48）这是一个以s 为变量的代数方程，方程右端是两部分的乘积；一部分是)(s U r ，这是外作用（输入量）的拉氏变换式，随)(t u r 的形式而改变；另一部分是11+RCs ，完全由网络的结构参数确定。

将上式（2-48）改写成如下形式 11)()(+=RCs s U s U r c 令11)(+=RCs s G ，则输出的拉氏变换式可写成 )()()(s U s G s U r c =可见，如果)(s U r 给定，则输出)(s U c 的特性完全由)(s G 决定。

)(s G 反映了系统（网络）自身的动态本质。

这很显然，因为)(s G 是由微分方程经拉氏变换得到的，而拉氏变换又是一种线性变换，只是将变量从实数t 域变换（映射）到复数s 域，所得结果不会改变原方程所反映的系统本质，对照)(s G 与原微分方程（2-44）的形式，也可看出二者的联系。

第六章 传递函数对于线性定常系统，传递函数是常用的一种数学模型，它是在拉氏变换的基础上建立的。

用传递函数描述系统可以免去求解微分方程的麻烦，间接地分析系统结构及参数与系统性能的关系，并且可以根据传递函数在复平面上的形状直接判断系统的动态性能，找出改善系统品质的方法。

因此，传递函数是经典控制理论的基础，是一个极其重要的基本概念。

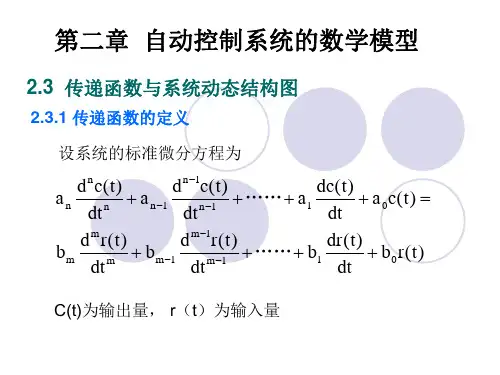
第一节 传递函数的定义一、传递函数的定义1、定义对于线性定常系统，在零初始条件下，系统输出量的拉氏变换与输入量的拉()()C s R s ==零初始条件输出信号的拉氏变换传递函数输入信号的拉氏变换2、推导设线性定常系统的微分方程的一般形式为1011110111()()()()()()()()n n n n nn m m m m mm d d d a c t a c t a c t a c t dtdtdtd d d b r t b r t b r t b r t dtdtdt------++⋅⋅⋅++=++⋅⋅⋅++◆ 式中c(t)是系统输出量，r(t)是系统输入量，r(t)、c(t)及其各阶导数在t=0时的值均为零，即零初始条件。

◆a ， 1a ，…，na 及b ， 1b ，…，mb 均为系统结构参数所决定的实常数。

对上式中各项分别求拉氏变换，并令C(s)＝L[c(t)]，R(s)=L[r(t)]，可得s 的代数方程为：11011011[]()[]()nn mm n n m m a s a sa s a C sb sb sb s b R s ----++⋅⋅⋅++=++⋅⋅⋅++于是，由定义得到系统的传递函数为：10111011()()()()()m m m m nn n nb s b sb s b C s M s G s R s a s a sa s a N s ----++⋅⋅⋅++===++⋅⋅⋅++其中，1011()m m m m M s b s b s b s b --=++⋅⋅⋅++ 1011()n n n n N s a s a s a s a --=++⋅⋅⋅++ N(s)=0称为系统的特征方程，其根称为系统特征根。

传递函数的概念传递函数是指零初始条件下线性系统响应（即输出）量的拉普拉斯变换（或z变换）与激励（即输入）量的拉普拉斯变换之比。

记作G（s）=Y（s）/U（s），其中Y（s）、U（s)分别为输出量和输入量的拉普拉斯变换。

传递函数是描述线性系统动态特性的基本数学工具之一，经典控制理论的主要研究方法——频率响应法和根轨迹法——都是建立在传递函数的基础之上。

传递函数是研究经典控制理论的主要工具之一。

基本释义把具有线性特性的对象的输入与输出间的关系，用一个函数（输出波形的拉普拉斯变换与输入波形的拉普拉斯变换之比）来表示的，称为传递函数。

原是控制工程学的用语，在生理学上往往用来表述心脏、呼吸器官、瞳孔等的特性。

系统的传递函数与描述其运动规律的微分方程是对应的。

可根据组成系统各单元的传递函数和它们之间的联结关系导出整体系统的传递函数，并用它分析系统的动态特性、稳定性，或根据给定要求综合控制系统，设计满意的控制器。

以传递函数为工具分析和综合控制系统的方法称为频域法。

它不但是经典控制理论的基础，而且在以时域方法为基础的现代控制理论发展过程中，也不断发展形成了多变量频域控制理论，成为研究多变量控制系统的有力工具。

传递函数中的复变量s在实部为零、虚部为角频率时就是频率响应。

传递函数也是《积分变换》里的概念。

对复参数s，函数f(t)*e^(-st)在（-∞，+∞）的积分，称为函数f(t)的（双边）拉普拉斯变换，简称拉氏变换（如果是在[0,+∞)内积分，则称为单边拉普拉斯变换，记作F(s)，这是个复变函数。

设一个系统的输入函数为x(t），输出函数为y(t)，则y(t)的拉氏变换Y(s)与x(t)的拉氏变换X(s)的商：W(s)=Y(s)/X(s)称为这个系统的传递函数。

传递函数是由系统的本质特性确定的，与输入量无关。

知道传递函数以后，就可以由输入量求输出量，或者根据需要的输出量确定输入量了。

传递函数的概念在自动控制理论里有重要应用。

传递函数的定义,零点,极点,特征方程【引言】在探讨传递函数的定义、零点、极点和特征方程之前，我们首先要了解传递函数的基本概念。

传递函数是描述线性时不变系统输入与输出之间关系的一种数学函数。

它是控制工程中最为常用的理论工具之一，对于分析和设计控制系统具有重要意义。

通过对传递函数的分析，我们可以全面了解系统的动态特性，从而帮助我们实现恰当的控制和优化。

【传递函数的定义】传递函数是描述线性时不变系统输入与输出之间关系的函数。

在控制工程中，一般使用 Laplace 变换来表示传递函数。

传递函数可以用来描述系统对输入信号的响应情况，其数学表达式通常具有分子和分母的形式，形如 H(s)=Y(s)/X(s)，其中 H(s) 为传递函数，Y(s) 为系统的输出信号的 Laplace 变换，X(s) 为系统的输入信号的 Laplace 变换。

通过传递函数，我们可以了解系统对各种输入信号的响应情况，从而为控制系统的设计和分析提供依据。

【零点和极点】传递函数的分子和分母多项式的根分别称为传递函数的零点和极点。

零点和极点决定了传递函数的动态特性，对于系统的稳定性和动态响应具有重要影响。

零点是使传递函数等于零的值，其位置可以直接影响系统的传递特性。

当传递函数的零点位于频域图中的某一点时，系统对该频率的输入信号会受到抑制；当零点位于实轴上时，系统会产生共振现象，从而导致系统的不稳定性。

极点是使传递函数的分母多项式等于零的值，其位置决定了系统的稳定性和动态响应。

当极点全部位于左半平面时，系统为稳定系统；当存在极点位于右半平面时，系统为不稳定系统；若存在虚轴上的极点，则会影响系统的频率响应特性。

【特征方程】特征方程可以由传递函数的分母多项式推导得出，是描述系统的稳定性及动态响应的重要方程之一。

特征方程的根即为传递函数的极点，通过解特征方程可以得到系统的固有频率和阻尼比，从而帮助我们全面了解系统的动态特性。

【个人观点】对于控制工程领域的从业者来说，深入理解传递函数的定义、零点、极点和特征方程对于系统分析和控制设计至关重要。