电路基本理论课后答案(哈工大版)第10章

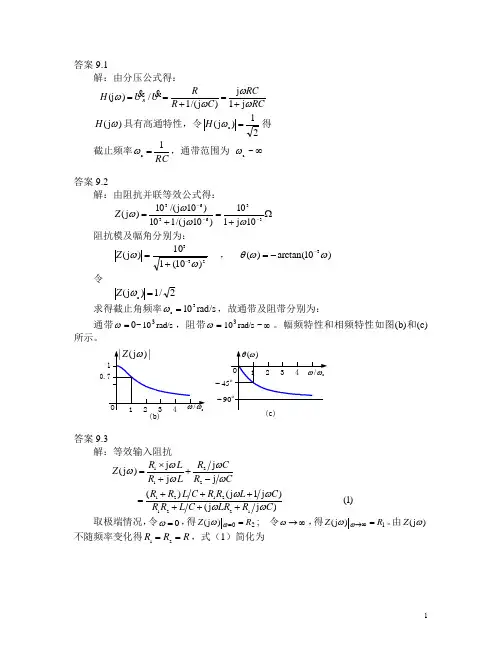
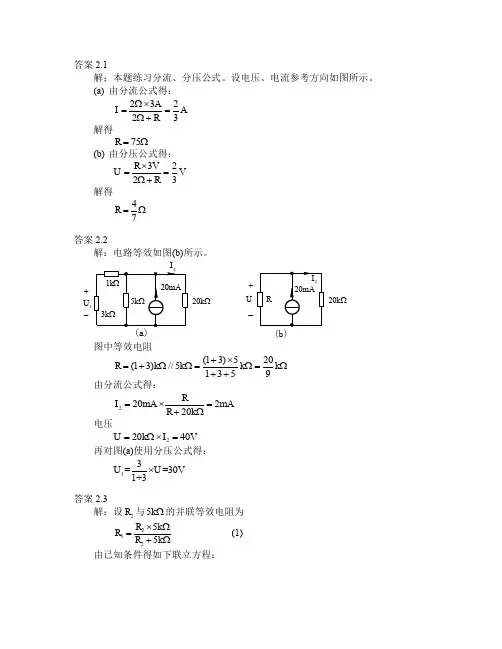
答案9.1解：由分压公式得：U U H R/)(j =ωRCRC C R R ωωωj 1j )j /(1+=+= )j (ωH 具有高通特性，令21)j (c =ωH 得截止频率RC1c =ω，通带范围为∞~c ω答案9.2解：由阻抗并联等效公式得：Ω+=+=---33636310j 110)10j /(110)10j /(10)j (ωωωωZ 阻抗模及幅角分别为：233)10(110)j (ωω-+=Z ， )10arctan()(3ωωθ--= 令2/1)j (c =ωZ求得截止角频率rad/s 103c =ω，故通带及阻带分别为：通带=ω0~rad/s 103，阻带=ωrad/s 103~∞。

幅频特性和相频特性如图(b)和(c)所示。

(b)--答案9.3解：等效输入阻抗)1()j j ()j 1j ()(j j j j )j (122121212211C R LR C L R R C L R R C L R R CR CR L R L R Z ωωωωωωωωω++++++=-++⨯=取极端情况，令0=ω，得20)j (R Z ==ωω; 令∞→ω，得1)j (R Z =∞→ωω。

由)j (ωZ 不随频率变化得R R R ==21，式（1）简化为)j 1j ()j 1j (2)j 1j ()j 1j (2)j (22C L RC L R C L R CL RC L R C L R C L R C L R Z ωωωωωωωωω+++++=+++++= 由)j (ωZ 为实数得：CL R R C L R R C L =+=2,2 故当C L R R ==21时端口电流与端口电压的波形相似，此时C L Z =)j (ω。

答案9.4解： RC 并联的等效阻抗RCRC R C R Z RC ωωωj 1j /1j /+=+=RC RCZ L Z U U H +==ωωj /)j (12 RL LC RC L R R /j 11)j 1(j 2ωωωω+-=++= 幅频特性222)/()1(1)j (R L LC H ωωω+-=当0→ω时，1)j (=ωH ；当∞→ω时，0)j (=ωH所以它具有低通特性。

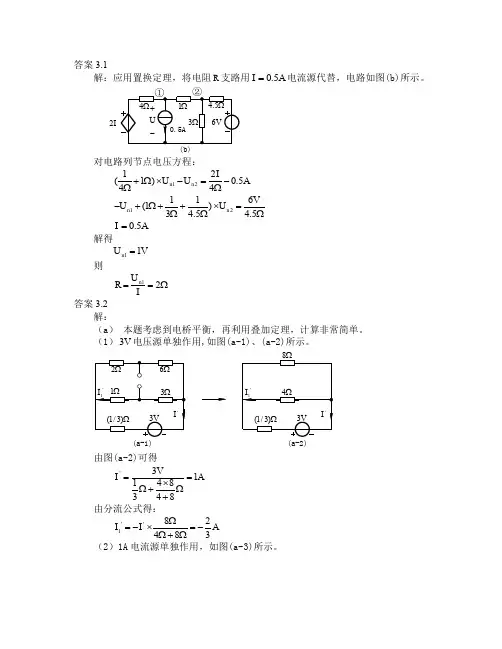
答案2.1解：本题练习分流、分压公式。

设电压、电流参考方向如图所示。

(a) 由分流公式得：23A 2A 23I R Ω⨯==Ω+解得75R =Ω(b) 由分压公式得：3V 2V 23R U R ⨯==Ω+解得47R =Ω答案2.2解：电路等效如图(b)所示。

20k Ω1U +-20k Ω(b)+_U图中等效电阻(13)520(13)k //5k k k 1359R +⨯=+ΩΩ=Ω=Ω++由分流公式得：220mA 2mA 20k RI R =⨯=+Ω电压220k 40V U I =Ω⨯= 再对图(a)使用分压公式得：13==30V 1+3U U ⨯答案2.3解：设2R 与5k Ω的并联等效电阻为2325k 5k R R R ⨯Ω=+Ω(1) 由已知条件得如下联立方程：32113130.05(2) 40k (3)eqR U UR R R R R ⎧==⎪+⎨⎪=+=Ω⎩由方程(2)、(3)解得138k R =Ω 32k R =Ω 再将3R 代入(1)式得210k 3R =Ω答案2.4解：由并联电路分流公式，得1820mA 8mA (128)I Ω=⨯=+Ω2620mA 12mA (46)I Ω=⨯=+Ω由节点①的KCL 得128mA 12mA 4mA I I I =-=-=-答案2.5解：首先将电路化简成图(b)。

图 题2.5120Ω(a)图中1(140100)240R =+Ω=Ω2(200160)120270360(200160)120R ⎡⎤+⨯=+Ω=Ω⎢⎥++⎣⎦ 由并联电路分流公式得211210A 6A R I R R =⨯=+及21104A I I =-= 再由图(a)得321201A 360120I I =⨯=+由KVL 得，3131200100400V U U U I I =-=-=-答案2.6xRx(a-1)图2.6解：（a ）设R 和r 为1级，则图题2.6(a)为2级再加x R 。

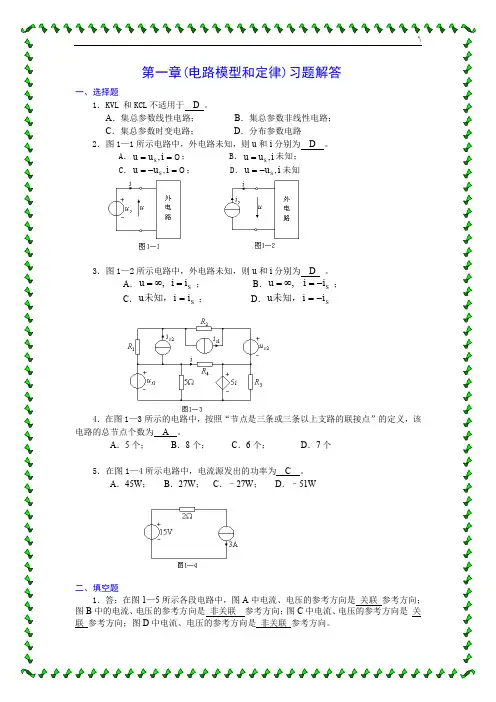
第一章(电路模型和定律)习题解答一、选择题1．KVL 和KCL 不适用于 D 。

A ．集总参数线性电路；B ．集总参数非线性电路；C ．集总参数时变电路；D ．分布参数电路2．图1—1所示电路中，外电路未知，则u 和i 分别为 D 。

A ．0==i u uS ,； B ．i u u S ,=未知；C ．0=-=i u uS ,； D ．i u u S ,-=未知3．图1—2所示电路中，外电路未知，则u 和i 分别为 D 。

A ．S i i u =∞=, ；B ．S i i u -=∞=, ；C ．S i i u =未知， ； D ．S i i u -=未知，4．在图1—3所示的电路中，按照“节点是三条或三条以上支路的联接点”的定义，该电路的总节点个数为 A 。

A ．5个；B ．8个；C ．6个；D ．7个5．在图1—4所示电路中，电流源发出的功率为 C 。

A ．45W ；B ．27W ；C ．–27W ；D ．–51W二、填空题1．答：在图1—5所示各段电路中，图A 中电流、电压的参考方向是 关联 参考方向；图B 中的电流、电压的参考方向是 非关联 参考方向；图C 中电流、电压的参考方向是 关联 参考方向；图D 中电流、电压的参考方向是 非关联 参考方向。

2．答：图1—6所示电路中的u 和i 对元件A 而言是 非关联 参考方向；对元件B 而言是 关联 参考方向。

3．答：在图1—7所示的四段电路中，A 、B 中的电压和电流为关联参考方向，C 、D中的电压和电流为非关联参考方向。

4．答：电路如图1—8所示。

如果10=R Ω，则10=U V ，9-=I A ；如果1=R Ω，则 10=U V ，0=I A 。

5．答：在图1—9 (a)所示的电路中，当10=R Ω时，=2u 50V ，=2i 5A ；当5=R Ω时，=2u 50V , =2i 10A 。

在图1—9 (b)所示的电路中，当R =10Ω时，2002=u V ,202=i A ；当5=R Ω时，1002=u V, 202=i A 。

答案10.1解：0<t 时，电容处于开路，故V 20k 2m A 10)0(=Ω⨯=-C u 由换路定律得：V 20)0()0(==-+C C u u换路后一瞬间，两电阻为串联，总电压为)0(+C u 。

所以m A 5k )22()0()0(1=Ω+=++C u i再由节点①的KCL 方程得：m A 5m A )510()0(m A 10)0(1=-=-=++i i C答案10.2解：0<t 时电容处于开路，电感处于短路，Ω3电阻与Ω6电阻相并联，所以A 3)363685(V45)0(=Ω+⨯++=-i ，A 2)0(366)0(=⨯+=--i i L V 24)0(8)0(=⨯=--i u C 由换路定律得：V 24)0()0(==-+C C u u ，A 2)0()0(==-+L L i i 由KVL 得开关电压：V 8V )2824()0(8)0()0(-=⨯+-=⨯+-=+++L C i u u 答案10.3解：0<t 时电容处于开路，0=i ，受控源源电压04=i ，所以V 6.0V 5.1)69(6)0()0()0(1=⨯Ω+Ω===--+u u u C C0>t 时，求等效电阻的电路如图(b)所示。

等效电阻Ω=++-==5)36(4i ii i i u R时间常数s 1.0i ==C R τ0>t 后电路为零输入响应，故电容电压为：V e 6.0e )0()(10/t t C C u t u --+==τΩ6电阻电压为：V e 72.0)d d (66)(101t Ctu Ci t u -=-⨯Ω-=⨯Ω-=)0(>t答案10.4解：0<t 时电感处于短路，故A 3A 9363)0(=⨯+=-L i ，由换路定律得： A 3)0()0(==-+L L i i求等效电阻的电路如图(b)所示。

(b)等效电阻Ω=+⨯+=836366i R ，时间常数s 5.0/i ==R L τ 0>t 后电路为零输入响应，故电感电流为A e 3e )0()(2/t t L L i t i --+==τ)0(≥t 电感电压V e 24d d )(21t L tiL t u --==)0(>tΩ3电阻电流为A e 23632133t L u i u i --=Ω+⨯Ω=Ω=Ω3电阻消耗的能量为：W 3]e 25.0[1212304040233=-==Ω=∞-∞-∞Ω⎰⎰t t dt e dt i W答案10.5解：由换路定律得0)0()0(==-+L L i i ，达到稳态时电感处于短路，故A 54/20)(==∞L i求等效电阻的电路如图(b)所示。

186第10章 二端口网络网络按其引出端子的数目可分为二端网络、三端网络及四端网络等，如果一个二端网络满足从一个端子流入的电流等于另一个端子上流出的电流时，就可称为一端口网络，如果电路中有两个一端口网络时就构成了一个二端口网络。

本章是把二端口网络当作一个整体，不研究其内部电路的工作状态，只研究端口电流、电压之间的关系，即端口的外特性。

联系这些关系的是一些参数。

这些参数只取决于网络本身的元件参数和各元件之间连接的结构形式。

一旦求出表征这个二端口网络的参数，就可以确定二端口网络各端口之间电流、电压的关系，进而对二端口网络的传输特性进行分析。

本章主要解决的问题是找出表征二端口网络的参数及由这些参数联系着的端口电流、电压方程，并在此基础上分析双口网络的电路。

本章教学要求理解二端口网络的概念，掌握二端口网络的特点，熟悉二端口网络的方程及参数，能较为熟练地计算参数，理解二端口网络等效的概念掌握其等效计算的方法，理解二端口网络的输入电阻、输出电阻及特性阻抗的定义及计算方法。

通过实验环节进一步加深理解二端口网络的基本概念和基本理论，掌握直流二端口网络传输参数的测量技术。

10.1 二端口网络的一般概念学习目标：熟悉二端口网络的判定，了解无源、有源、线性、非线性二端口网络在组成上的不同点。

在对直流电路的分析过程中，我们通过戴维南定理讲述了具有两个引线端的电路的分析方法，这种具有两个引线端的电路称为一端口网络，如图10.1（a ）所示。

一个一端口网络，不论其内部电路简单或复杂，就其外特性来说，可以用一个具有一定内阻的电源进行置换，以便在分析某个局部电路工作关系时，使分析过程得到简化。

当一个电路有四个外引线端子，如图10.1（b ）所示，其中左、右两对端子都满足：从一个引线端流入电路的电流与另一个引线端流出电路的电流相等的条件，这样组成的电路可称为二端口网络（或称为双口网络）。

（a ）一端口网络 （b ）二端口网络图10.1 端口网络2U ＋_ _187当一个二端口网络的端口处电流与电压满足线性关系时，则该二端口网络称为线性二端口网络。

答案10.1解：0<t 时，电容处于开路，故V 20k 2m A 10)0(=Ω⨯=-C u由换路定律得：V 20)0()0(==-+C C u u换路后一瞬间，两电阻为串联，总电压为)0(+C u 。

所以m A 5k )22()0()0(1=Ω+=++C u i再由节点①的KCL 方程得：m A 5m A )510()0(m A 10)0(1=-=-=++i i C答案10.2解：0<t 时电容处于开路，电感处于短路，Ω3电阻与Ω6电阻相并联，所以A 3)363685(V45)0(=Ω+⨯++=-i ，A 2)0(366)0(=⨯+=--i i L V 24)0(8)0(=⨯=--i u C 由换路定律得：V 24)0()0(==-+C C u u ，A 2)0()0(==-+L L i i 由KVL 得开关电压：V 8V )2824()0(8)0()0(-=⨯+-=⨯+-=+++L C i u u 答案10.3解：0<t 时电容处于开路，0=i ，受控源源电压04=i ，所以V 6.0V 5.1)69(6)0()0()0(1=⨯Ω+Ω===--+u u u C C0>t 时，求等效电阻的电路如图(b)所示。

等效电阻Ω=++-==5)36(4i ii i i u R时间常数s 1.0i ==C R τ0>t 后电路为零输入响应，故电容电压为：V e 6.0e )0()(10/t t C C u t u --+==τΩ6电阻电压为：V e 72.0)d d (66)(101t Ctu Ci t u -=-⨯Ω-=⨯Ω-=)0(>t答案10.4解：0<t 时电感处于短路，故A 3A 9363)0(=⨯+=-L i ，由换路定律得： A 3)0()0(==-+L L i i求等效电阻的电路如图(b)所示。

(b)等效电阻Ω=+⨯+=836366i R ，时间常数s 5.0/i ==R L τ 0>t 后电路为零输入响应，故电感电流为A e 3e )0()(2/t t L L i t i --+==τ)0(≥t 电感电压V e 24d d )(21t L tiL t u --==)0(>tΩ3电阻电流为A e 23632133t L u i u i --=Ω+⨯Ω=Ω=Ω3电阻消耗的能量为：W 3]e 25.0[1212304040233=-==Ω=∞-∞-∞Ω⎰⎰t t dt e dt i W答案10.5解：由换路定律得0)0()0(==-+L L i i ，达到稳态时电感处于短路，故A 54/20)(==∞L i求等效电阻的电路如图(b)所示。

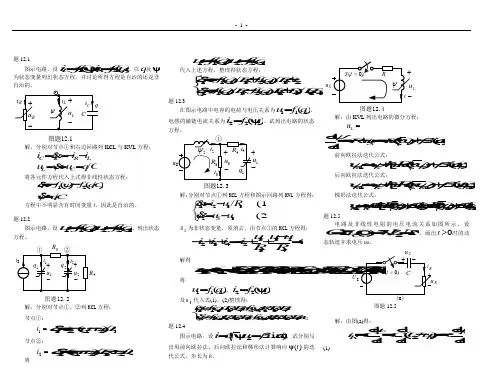
题12.1图示电路，设)(),(21R R L u f i f i ==ψ。

以q 及ψ为状态变量列出状态方程，并讨论所得方程是自治的还是非自治的。

图题12.1解：分别对节点①和右边回路列KCL 与KVL 方程：C q u u i i q i CL L R C C /===--==ψ将各元件方程代入上式得非线性状态方程：Cq C q f f q /)/()(21=--=ψψ方程中不明显含有时间变量t ，因此是自治的。

题12.2图示电路，设)(),(222111q f u q f u ==，列出状态方程。

4R R 图题12.2解：分别对节点①、②列KCL 方程： 节点①：=1i 321S 1/)(R u u i q --= 节点②：=2i 423212//)(R u R u u q --= 将)(),(222111q f u q f u == 代入上述方程，整理得状态方程：⎩⎨⎧+-=++-=)/())((/)(/)(/)(4343223112S3223111R R R R q f R q f q i R q f R q f q 题12.3在图示电路中电容的电荷与电压关系为)(111q f u =，电感的磁链电流关系为)(222ψf i =。

试列出电路的状态方程。

1u u 图题12.3解：分别对节点①列KCL 方程和图示回路列KVL 方程得：⎩⎨⎧-=-=(2) (1) /323321u u R u i q S ψ3u 为非状态变量，须消去。

由节点①的KCL 方程得：0413332432=-++-=++-R u u R u i i i i 解得()([)/()(224114332413f R q f R R R i R u u +=++=将)(111q f u =、)(222ψf i = 及3u 代入式(1)、(2)整理得：⎩⎨⎧++-+-=+++-=S u R R R R f R R R q f R R R f R R q f q )/()()/()()/()()/()(4343224331124332243111ψψψ 题12.4图示电路，设)sin(,S 3t u a i ωβ==ψ，试分别写出用前向欧拉法、后向欧拉法和梯形法计算响应)(t ψ的迭代公式，步长为h 。

第一章习题图示元件当时间t<2s时电流为2A，从a流向b；当t>2s时为3A，从b流向a。

根据图示参考方向，写出电流的数学表达式。

图示元件电压u=(5-9e-t/t)V，t>0。

分别求出t=0 和t→¥时电压u的代数值及其真实方向。

图题图题图示电路。

设元件A消耗功率为10W，求；设元件B消耗功率为-10W,求；设元件C发出功率为-10W，求。

图题求图示电路电流。

若只求，能否一步求得图示电路，已知部分电流值和部分电压值。

(1) 试求其余未知电流。

若少已知一个电流，能否求出全部未知电流(2) 试求其余未知电压u14、u15、u52、u53。

若少已知一个电压，能否求出全部未知电压图示电路，已知,,,。

求各元件消耗的功率。

图示电路，已知，。

求(a)、(b)两电路各电源发出的功率和电阻吸收的功率。

求图示电路电压。

求图示电路两个独立电源各自发出的功率。

求网络N吸收的功率和电流源发出的功率。

求图示电路两个独立电源各自发出的功率。

求图示电路两个受控源各自发出的功率。

图示电路，已知电流源发出的功率是12W，求r的值。

求图示电路受控源和独立源各自发出的功率。

图示电路为独立源、受控源和电阻组成的一端口。

试求出其端口特性，即关系。

讨论图示电路中开关S开闭对电路中各元件的电压、电流和功率的影响，加深对独立源特性的理解。

第二章习题图(a)电路，若使电流A,，求电阻；图(b)电路，若使电压U=(2/3)V，求电阻R。

求图示电路的电压及电流。

图示电路中要求，等效电阻。

求和的值。

求图示电路的电流I。

求图示电路的电压U。

求图示电路的等效电阻。

求图示电路的最简等效电源。

图题利用等效变换求图示电路的电流I。

(a) (b)图题求图示电路的等效电阻R。

求图示电路的电流和。

列写图示电路的支路电流方程。

图题图示电路，分别按图(a)、(b)规定的回路列出支路电流方程。

图题用回路电流法求图示电路的电流I。

用回路电流法求图示电路的电流I。

第一章习题图示元件当时间t<2s时电流为2A，从a流向b；当t>2s时为3A，从b流向a。

根据图示参考方向，写出电流的数学表达式。

图示元件电压u=(5-9e-t/t)V，t>0。

分别求出t=0 和t→¥时电压u的代数值及其真实方向。

图题图题图示电路。

设元件A消耗功率为10W，求；设元件B消耗功率为-10W,求；设元件C 发出功率为-10W，求。

图题求图示电路电流。

若只求，能否一步求得？图示电路，已知部分电流值和部分电压值。

(1) 试求其余未知电流。

若少已知一个电流，能否求出全部未知电流？(2) 试求其余未知电压u14、u15、u52、u53。

若少已知一个电压，能否求出全部未知电压？图示电路，已知,,,。

求各元件消耗的功率。

图示电路，已知，。

求(a)、(b)两电路各电源发出的功率和电阻吸收的功率。

求图示电路电压。

求图示电路两个独立电源各自发出的功率。

求网络N吸收的功率和电流源发出的功率。

求图示电路两个独立电源各自发出的功率。

求图示电路两个受控源各自发出的功率。

图示电路，已知电流源发出的功率是12W，求r的值。

求图示电路受控源和独立源各自发出的功率。

图示电路为独立源、受控源和电阻组成的一端口。

试求出其端口特性，即关系。

讨论图示电路中开关S开闭对电路中各元件的电压、电流和功率的影响，加深对独立源特性的理解。

第二章习题图(a)电路，若使电流A,，求电阻；图(b)电路，若使电压U=(2/3)V，求电阻R。

求图示电路的电压及电流。

图示电路中要求，等效电阻。

求和的值。

求图示电路的电流I。

求图示电路的电压U。

求图示电路的等效电阻。

求图示电路的最简等效电源。

图题利用等效变换求图示电路的电流I。

(a) (b)图题求图示电路的等效电阻R。

求图示电路的电流和。

列写图示电路的支路电流方程。

图题图示电路，分别按图(a)、(b)规定的回路列出支路电流方程。

图题用回路电流法求图示电路的电流I。

用回路电流法求图示电路的电流I。

第6章 逻辑代数基础6.2 授课的几点建议6.2.1 基本逻辑关系的描述基本逻辑关系有“与”、“或”、“非”三种，在本教材中采用文字叙述和常开触点、常闭触点的串、并联等形式来加以描述。

还有一种描述逻辑关系的图，称为文氏图（V enn diagram ）。

图6.1(a)圆圈内是A ，圆圈外是A ；图6.1(b)圆圈A 与圆圈B 相交的部分是A 、B 的与逻辑，即AB ；图6.1(c)圆圈A 与圆圈B 所有的部分是A 、B 的或逻辑，即A +B 。

与逻辑AB 也称为A 与B 的交集（intersection ）；或逻辑A +B 也称为A 和B 的并集（union ）。

(a) 单变量的文氏图 (b) 与逻辑的文氏图 (c) 图6.1 文氏图6.2.2 正逻辑和负逻辑的关系正逻辑是将双值逻辑的高电平H 定义为“1”，代表有信号；低电平L 定义为“0”，代表无信号。

负逻辑是将双值逻辑的高电平H 定义为“0”，代表无信号；低电平L 定义为“1”，代表有信号。

正逻辑和负逻辑对信号有无的定义正好相反，就好象“左”、“右”的规定一样，设正逻辑符合现在习惯的规定，而负逻辑正好反过来，把现在是“左”，定义为“右”，把现在是“右”，定义为“左”。

关于正、负逻辑的真值表，以两个变量为例，见表6.1。

表6.1由表6.1可以看出，对正逻辑的约定，表中相当是与逻辑；对负逻辑约定，则相当是或逻辑。

所以正逻辑的“与”相当负逻辑的“或”；正逻辑的“或”相当负逻辑的“与”。

正与和负或只是形式上的不同，不改变问题的实质。

6.2.3 形式定理本书介绍了17个形式定理，分成五类。

需要说明的是，许多书上对这些形式定理有各自的名称，可能是翻译上的缘故，有一些不太贴切，为此，将形式定理分成5种形式表述，更便于记忆。

所以称为形式定理，是因为这些定理在逻辑关系的形式上虽然不同，但实质上是相等的。

形式定理主要用于逻辑式的化简，或者在形式上对逻辑式进行变换，它有以下五种类型：1．变量与常量之间的关系；2．变量自身之间的关系；3．与或型的逻辑关系；4．或与型的逻辑关系；5．求反的逻辑关系——摩根（Morgan ）定理。