哈工大电路理论基础课后习题答案9

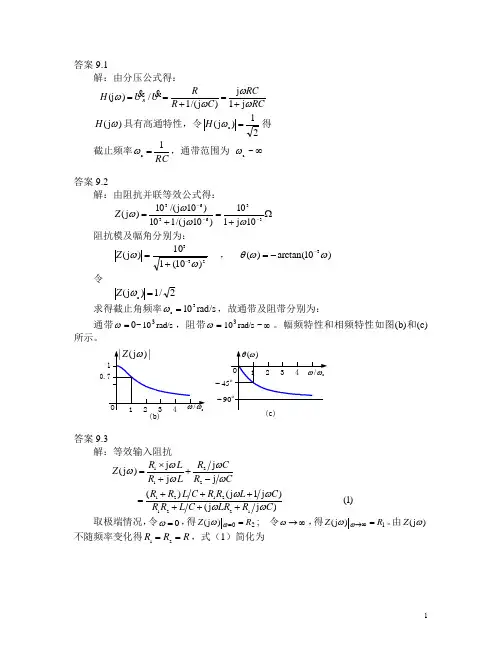
答案9.1解：由分压公式得：U U H R/)(j =ωRCRC C R R ωωωj 1j )j /(1+=+= )j (ωH 具有高通特性，令21)j (c =ωH 得截止频率RC1c =ω，通带范围为∞~c ω答案9.2解：由阻抗并联等效公式得：Ω+=+=---33636310j 110)10j /(110)10j /(10)j (ωωωωZ 阻抗模及幅角分别为：233)10(110)j (ωω-+=Z ， )10arctan()(3ωωθ--= 令2/1)j (c =ωZ求得截止角频率rad/s 103c =ω，故通带及阻带分别为：通带=ω0~rad/s 103，阻带=ωrad/s 103~∞。

幅频特性和相频特性如图(b)和(c)所示。

(b)--答案9.3解：等效输入阻抗)1()j j ()j 1j ()(j j j j )j (122121212211C R LR C L R R C L R R C L R R CR CR L R L R Z ωωωωωωωωω++++++=-++⨯=取极端情况，令0=ω，得20)j (R Z ==ωω; 令∞→ω，得1)j (R Z =∞→ωω。

由)j (ωZ 不随频率变化得R R R ==21，式（1）简化为)j 1j ()j 1j (2)j 1j ()j 1j (2)j (22C L RC L R C L R CL RC L R C L R C L R C L R Z ωωωωωωωωω+++++=+++++= 由)j (ωZ 为实数得：CL R R C L R R C L =+=2,2 故当C L R R ==21时端口电流与端口电压的波形相似，此时C L Z =)j (ω。

答案9.4解： RC 并联的等效阻抗RCRC R C R Z RC ωωωj 1j /1j /+=+=RC RCZ L Z U U H +==ωωj /)j (12 RL LC RC L R R /j 11)j 1(j 2ωωωω+-=++= 幅频特性222)/()1(1)j (R L LC H ωωω+-=当0→ω时，1)j (=ωH ；当∞→ω时，0)j (=ωH所以它具有低通特性。

第9章 线性动态电路暂态过程的复频域分析9.1根据定义求()()f t t t ε=和()e ()at f t t t ε-=的象函数。

解：(1)2020001e 1d e 1e d e )()(-s s t s stt t t s F stst stst =-=+-==∞-∞-∞-∞----⎰⎰ε (2)20)(20)(00)(1e)(1d e 1e d e )(e )(-ααααεααα+=+-=+++-==∞+-∞+-∞-∞-----⎰⎰s s ts s t t t t s F ts t s st st t9.2 求下列函数的原函数。

(a)6512)(2+++=s s s s F ， (b) )2)(1(795)(23+++++=s s s s s s F ， (c) 623)(2++=s s s F 。

解：(a) 6512)(2+++=s s s s F 3221+++=s A s A 3|31221-=++=-=s s s A ， 3|31221-=++=-=s s s A所以 t t s s t f 321e 5e 3}3523{)(---+-=+++-=L(b))2)(1(795)(23+++++=s s s s s s F 212)2)(1(3221+++++=+++++=s A s A s s s s s 2|2311=++=-=s s s A 1|1321-=++=-=s s s A 所以 t t t t s s s L t f 21e e 2)(2)(}21122{)(----++'=+-++++=δδ(c)623)(2++=s s s F 22)5()1(5)5/3(++⨯=s ， 查表得)5sin(e 53)(t t f t -= 9.3求图示电路的等效运算阻抗。

图题9.3解：由运算电路(略)求得端口等效运算阻抗为：11262241)3/(142)]3/(14[21)(22i ++++=++++=s s ss s s s s s Z ， 112611430)(22++++=s s s s s Z i 9.4 图示电路，已知2S e ()t u t ε-=V ，求零状态响应u 。

第6章 逻辑代数基础6.2 授课的几点建议6.2.1 基本逻辑关系的描述基本逻辑关系有“与”、“或”、“非”三种，在本教材中采用文字叙述和常开触点、常闭触点的串、并联等形式来加以描述。

还有一种描述逻辑关系的图，称为文氏图（V enn diagram ）。

图6.1(a)圆圈内是A ，圆圈外是A ；图6.1(b)圆圈A 与圆圈B 相交的部分是A 、B 的与逻辑，即AB ；图6.1(c)圆圈A 与圆圈B 所有的部分是A 、B 的或逻辑，即A +B 。

与逻辑AB 也称为A 与B 的交集（intersection ）；或逻辑A +B 也称为A 和B 的并集（union ）。

(a) 单变量的文氏图 (b) 与逻辑的文氏图 (c) 图6.1 文氏图6.2.2 正逻辑和负逻辑的关系正逻辑是将双值逻辑的高电平H 定义为“1”，代表有信号；低电平L 定义为“0”，代表无信号。

负逻辑是将双值逻辑的高电平H 定义为“0”，代表无信号；低电平L 定义为“1”，代表有信号。

正逻辑和负逻辑对信号有无的定义正好相反，就好象“左”、“右”的规定一样，设正逻辑符合现在习惯的规定，而负逻辑正好反过来，把现在是“左”，定义为“右”，把现在是“右”，定义为“左”。

关于正、负逻辑的真值表，以两个变量为例，见表6.1。

表6.1由表6.1可以看出，对正逻辑的约定，表中相当是与逻辑；对负逻辑约定，则相当是或逻辑。

所以正逻辑的“与”相当负逻辑的“或”；正逻辑的“或”相当负逻辑的“与”。

正与和负或只是形式上的不同，不改变问题的实质。

6.2.3 形式定理本书介绍了17个形式定理，分成五类。

需要说明的是，许多书上对这些形式定理有各自的名称，可能是翻译上的缘故，有一些不太贴切，为此，将形式定理分成5种形式表述，更便于记忆。

所以称为形式定理，是因为这些定理在逻辑关系的形式上虽然不同，但实质上是相等的。

形式定理主要用于逻辑式的化简，或者在形式上对逻辑式进行变换，它有以下五种类型：1．变量与常量之间的关系；2．变量自身之间的关系；3．与或型的逻辑关系；4．或与型的逻辑关系；5．求反的逻辑关系——摩根（Morgan ）定理。

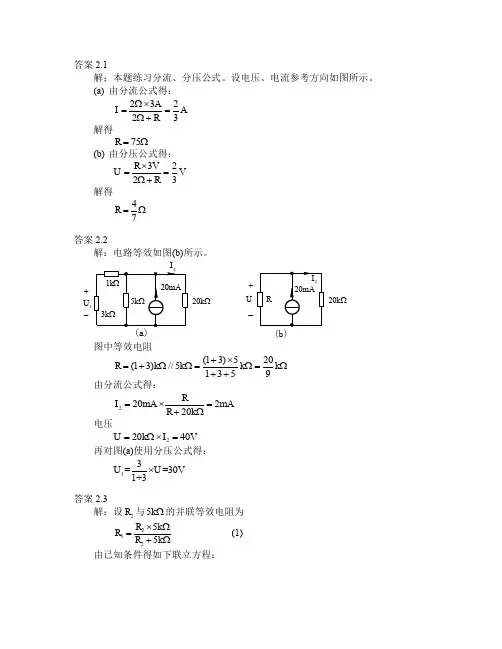
答案2.1解：本题练习分流、分压公式。

设电压、电流参考方向如图所示。

(a) 由分流公式得：23A 2A 23I R Ω⨯==Ω+解得75R =Ω(b) 由分压公式得：3V 2V 23R U R ⨯==Ω+解得47R =Ω答案2.2解：电路等效如图(b)所示。

20k Ω1U +-20k Ω(b)+_U图中等效电阻(13)520(13)k //5k k k 1359R +⨯=+ΩΩ=Ω=Ω++由分流公式得：220mA 2mA 20k RI R =⨯=+Ω电压220k 40V U I =Ω⨯= 再对图(a)使用分压公式得：13==30V 1+3U U ⨯答案2.3解：设2R 与5k Ω的并联等效电阻为2325k 5k R R R ⨯Ω=+Ω(1) 由已知条件得如下联立方程：32113130.05(2) 40k (3)eqR U UR R R R R ⎧==⎪+⎨⎪=+=Ω⎩由方程(2)、(3)解得138k R =Ω 32k R =Ω 再将3R 代入(1)式得210k 3R =Ω答案2.4解：由并联电路分流公式，得1820mA 8mA (128)I Ω=⨯=+Ω2620mA 12mA (46)I Ω=⨯=+Ω由节点①的KCL 得128mA 12mA 4mA I I I =-=-=-答案2.5解：首先将电路化简成图(b)。

图 题2.5120Ω(a)图中1(140100)240R =+Ω=Ω2(200160)120270360(200160)120R ⎡⎤+⨯=+Ω=Ω⎢⎥++⎣⎦ 由并联电路分流公式得211210A 6A R I R R =⨯=+及21104A I I =-= 再由图(a)得321201A 360120I I =⨯=+由KVL 得，3131200100400V U U U I I =-=-=-答案2.6xRx(a-1)图2.6解：（a ）设R 和r 为1级，则图题2.6(a)为2级再加x R 。

第一章(电路模型和定律)习题解答一、选择题1．KVL 和KCL 不适用于 D 。

A ．集总参数线性电路；B ．集总参数非线性电路；C ．集总参数时变电路；D ．分布参数电路2．图1—1所示电路中，外电路未知，则u 和i 分别为 D 。

A ．0==i u uS ,； B ．i u u S ,=未知；C ．0=-=i u uS ,； D ．i u u S ,-=未知3．图1—2所示电路中，外电路未知，则u 和i 分别为 D 。

A ．S i i u =∞=, ；B ．S i i u -=∞=, ；C ．S i i u =未知， ； D ．S i i u -=未知，4．在图1—3所示的电路中，按照“节点是三条或三条以上支路的联接点”的定义，该电路的总节点个数为 A 。

A ．5个；B ．8个；C ．6个；D ．7个5．在图1—4所示电路中，电流源发出的功率为 C 。

A ．45W ；B ．27W ；C ．–27W ；D ．–51W二、填空题1．答：在图1—5所示各段电路中，图A 中电流、电压的参考方向是 关联 参考方向；图B 中的电流、电压的参考方向是 非关联 参考方向；图C 中电流、电压的参考方向是 关联 参考方向；图D 中电流、电压的参考方向是 非关联 参考方向。

2．答：图1—6所示电路中的u 和i 对元件A 而言是 非关联 参考方向；对元件B 而言是 关联 参考方向。

3．答：在图1—7所示的四段电路中，A 、B 中的电压和电流为关联参考方向，C 、D中的电压和电流为非关联参考方向。

4．答：电路如图1—8所示。

如果10=R Ω，则10=U V ，9-=I A ；如果1=R Ω，则 10=U V ，0=I A 。

5．答：在图1—9 (a)所示的电路中，当10=R Ω时，=2u 50V ，=2i 5A ；当5=R Ω时，=2u 50V , =2i 10A 。

在图1—9 (b)所示的电路中，当R =10Ω时，2002=u V ,202=i A ；当5=R Ω时，1002=u V, 202=i A 。

答案10.1解：0<t 时，电容处于开路，故V 20k 2m A 10)0(=Ω⨯=-C u 由换路定律得：V 20)0()0(==-+C C u u换路后一瞬间，两电阻为串联，总电压为)0(+C u 。

所以m A 5k )22()0()0(1=Ω+=++C u i再由节点①的KCL 方程得：m A 5m A )510()0(m A 10)0(1=-=-=++i i C答案10.2解：0<t 时电容处于开路，电感处于短路，Ω3电阻与Ω6电阻相并联，所以A 3)363685(V45)0(=Ω+⨯++=-i ，A 2)0(366)0(=⨯+=--i i L V 24)0(8)0(=⨯=--i u C 由换路定律得：V 24)0()0(==-+C C u u ，A 2)0()0(==-+L L i i 由KVL 得开关电压：V 8V )2824()0(8)0()0(-=⨯+-=⨯+-=+++L C i u u 答案10.3解：0<t 时电容处于开路，0=i ，受控源源电压04=i ，所以V 6.0V 5.1)69(6)0()0()0(1=⨯Ω+Ω===--+u u u C C0>t 时，求等效电阻的电路如图(b)所示。

等效电阻Ω=++-==5)36(4i ii i i u R时间常数s 1.0i ==C R τ0>t 后电路为零输入响应，故电容电压为：V e 6.0e )0()(10/t t C C u t u --+==τΩ6电阻电压为：V e 72.0)d d (66)(101t Ctu Ci t u -=-⨯Ω-=⨯Ω-=)0(>t答案10.4解：0<t 时电感处于短路，故A 3A 9363)0(=⨯+=-L i ，由换路定律得： A 3)0()0(==-+L L i i求等效电阻的电路如图(b)所示。

(b)等效电阻Ω=+⨯+=836366i R ，时间常数s 5.0/i ==R L τ 0>t 后电路为零输入响应，故电感电流为A e 3e )0()(2/t t L L i t i --+==τ)0(≥t 电感电压V e 24d d )(21t L tiL t u --==)0(>tΩ3电阻电流为A e 23632133t L u i u i --=Ω+⨯Ω=Ω=Ω3电阻消耗的能量为：W 3]e 25.0[1212304040233=-==Ω=∞-∞-∞Ω⎰⎰t t dt e dt i W答案10.5解：由换路定律得0)0()0(==-+L L i i ，达到稳态时电感处于短路，故A 54/20)(==∞L i求等效电阻的电路如图(b)所示。

第九章 三相电路（部分习题参考答案）9.1 A m cos 2u U t ω=，，C m cos(2120)u U t ω=−oB m cos(2240)u U t ω=−o9.2 相电压为198V ，相电流为6.10A 9.3 220VAXU &BYUU &AYU &9.4440VU &U &AX&ACU &9.5 (1)ϕ2=120°，ϕ3= −120°；(2) A'B'45A I =o&，B'C'165A I =o&，C'A'75A I =−o&；(3) A 15A I =o&，B 135A I =o&，C105A I =−o& 9.6 (1) ，，； A'N'2053.13V U =∠−o &B'N'20173.13V U =∠−o &C'N'2066.87V U =∠o & (2) ，， AB 34.623.13V U =∠−o &BC 34.6143.13V U =∠−o &CA34.696.87V U =∠o &9.7 ， ； A 15.8337.7A I =∠−o &A N202.80.96V U ′′=∠o & ， ； B 15.83157.7A I =∠−o &B N202.8119.04V U ′′=∠−o &C 15.8382.3A I =∠o &， C N202.8120.96V U ′′=∠o &9.8 ，，； A 28.1739.8A I =∠−o &B 28.17159.8A I =∠−o &C28.1780.2A I =∠o &A B 16.269.8A I ′′=∠−o &，，； B C 16.26129.8A I ′′=∠−o &C A 16.26110.2A I ′′=∠o &A B312.328.86A U′′=∠o &，， B C312.391.14A U ′′=∠−o &C A312.3148.86A U ′′=∠o &9.9110V9.10 (a) 电流表读数为0， (b) 电流表读数为220A 9.11 l I =9.12 1()R C L += 9.13 电流表A 1的读数为0.591A ，电流表A 2的读数为0.318A ， 电流表A 3的读数为0.318A ，电流表A 0的读数为0.364A9.14 (1)，(2)A B ''4cos15 3.86A I I ==≈o A '2A I =，B 'I =9.15 ，电源连接方式改变不会影响结果。

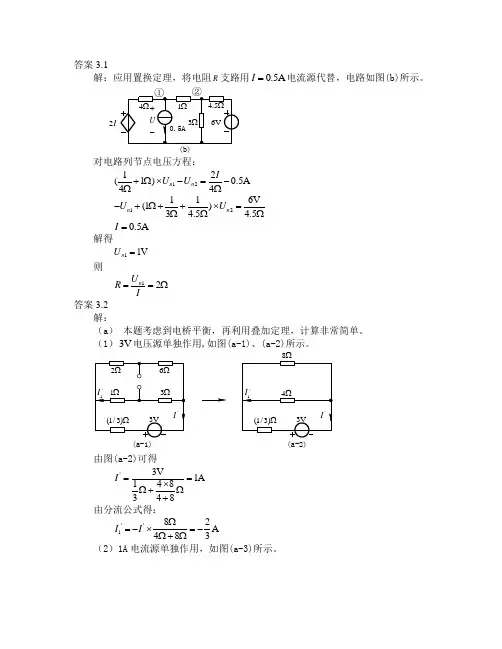
答案3.1解：应用置换定理，将电阻R 支路用0.5A I =电流源代替，电路如图(b)所示。

I2对电路列节点电压方程：1212(1)0.5A 44n n I U U +Ω⨯-=-ΩΩ12116V(1)3 4.5 4.5n n U U -+Ω++⨯=ΩΩΩ0.5A I = 解得11V n U = 则12n UR I==Ω答案3.2解：（a ）本题考虑到电桥平衡，再利用叠加定理，计算非常简单。

（1）3V 电压源单独作用,如图(a-1)、(a-2)所示。

(a-1)(a-2)由图(a-2)可得'3V1A 148348I ==⨯Ω+Ω+由分流公式得：''182A 483I I Ω=-⨯=-Ω+Ω（2）1A 电流源单独作用，如图(a-3)所示。

(a-3)考虑到电桥平衡，"0I =，在由分流公式得："1131A A 134I =-⨯=-+（3）叠加：'"1A I I I =+='"11117/12A I I I =+=-2111 2.007W P I Ω=⨯=（b ）（1）4V 电压源单独作用，如图(b-1)所示。

'2I '(b-1)由图(b-1)可得，'24V 2V (2+2)U Ω⨯==Ω'136A I U =-=-''21'5A I I I =+=-（2）2A 电流源单独作用，如图(b-2)所示。

(b-2)''222A=2V 22U ⨯=Ω⨯+ "''2311A 2I I =⨯= 对节点②列KCL 方程得，"""1132A 4A I U I +==对节点③列KCL 方程得，"""230I I U ++=解得"5A I =（3）叠加'"1116A 4A=10A I I I =+=---'"5A 5A=10A I I I =+=---2111100W P I Ω=⨯Ω= 答案3.3解：利用叠加定理，含源电阻网络中的电源分为一组，其作用为'I ，如图(b)所示。

电路理论基础习题答案第一章1-1. (a)、(b)吸收10W ；(c)、(d)发出10W. 1-2. –1A; –10V; –1A; – 4mW.1-3. –0.5A; –6V; –15e –t V; 1.75cos2t A; 3Ω; 1.8cos 22t W.1-4. u =104 i ; u = -104 i ; u =2000i ; u = -104 i ; 1-5.1-6. 0.1A. 1-7.1-8. 2F; 4C; 0; 4J. 1-9. 9.6V,0.192W, 1.152mJ; 16V , 0, 3.2mJ.1-10. 1– e -106t A , t >0 取s .1-11. 3H, 6(1– t )2 J; 3mH, 6(1–1000 t ) 2 mJ;1-12. 0.4F, 0 .1-13. 供12W; 吸40W;吸2W; (2V)供26W, (5A)吸10W. 1-14. –40V , –1mA; –50V, –1mA; 50V , 1mA. 1-15. 0.5A,1W; 2A,4W; –1A, –2W; 1A,2W. 1-16. 10V ,50W;50V ,250W;–3V ,–15W;2V ,10W. 1-17. (a)2V;R 耗4/3W;U S : –2/3W, I S : 2W; (b) –3V; R 耗3W; U S : –2W, I S :5W; (c)2V ,–3V; R 耗4W;3W;U S :2W, I S :5W; 1-18. 24V , 发72W; 3A, 吸15W;24V 电压源; 3A ↓电流源或5/3Ω电阻. 1-19. 0,U S /R L ,U S ;U S /R 1 ,U S /R 1 , –U S R f /R 1 . 1-20. 6A, 4A, 2A, 1A, 4A; 8V, –10V , 18V . 1-21. K 打开：(a)0, 0, 0; (b)10V , 0, 10V; (c)10V,10V ,0; K 闭合: (a)10V ,4V ,6V; (b)4V ,4V ,0; (c)4V,0,4V; 1-22. 2V; 7V; 3.25V; 2V. 1-23. 10Ω.1-24. 14V .1-25. –2.333V , 1.333A; 0.4V , 0.8A.1-26. 12V , 2A, –48W; –6V , 3A, –54W . ※第二章2-1. 2.5Ω; 1.6R ; 8/3Ω; 0.5R ; 4Ω; 1.448Ω; . R /8; 1.5Ω; 1.269Ω; 40Ω; 14Ω. 2-2. 11.11Ω; 8Ω; 12.5Ω. 2-3. 1.618Ω.2-4. 400V;363.6V;I A =.5A, 电流表及滑线电阻损坏. 2-6. 5k Ω. 2-7. 0.75Ω.2-8. 10/3A,1.2Ω;–5V ,3Ω; 8V ,4Ω; 0.5A,30/11Ω. 2-9. 1A,2Ω; 5V,2Ω; 2A; 2A; 2A,6Ω. 2-10. –75mA; –0.5A.2-11. 6Ω; 7.5Ω; 0; 2.1Ω. 2-12. 4Ω; 1.5Ω; 2k Ω. 2-13. 5.333A; 4.286A. 2-14. (a) –1 A ↓; (b) –2 A ↓, 吸20W. 2-16. 3A. 2-17. 7.33V . 2-18. 86.76W. 2-19. 1V , 4W. 2-20. 64W.2-21. 15A, 11A, 17A. 2-23. 7V , 3A; 8V ,1A. 2-24. 4V , 2.5V, 2V. 2-26. 60V . 2-27. 4.5V. 2-28. –18V .2-29. 原构成无解的矛盾方程组; (改后)4V ,10V . 2-30. 3.33 k , 50 k . 2-31. R 3 (R 1 +R 2 ) i S /R 1 .2-32. 可证明 I L =－u S /R 3 . 2-33. –2 ; 4 .2-34. (u S1 + u S2 + u S3 )/3 . ※第三章3-1. –1+9=8V; 6+9=15V; sin t +0.2 e – t V. 3-2. 155V . 3-3. 190mA.i A0 s 1 12 3 1-e -t t 0 t ms i mA 410 0 t ms p mW 4 100 2 25i , A 0.4 .75 t 0 .25 1.25 ms -0.4 (d) u , V 80 0 10-20 t , ms(f ) u , V 1000 10 t , ms (e)p (W) 100 1 2 t (s) -103-4. 1.8倍.3-5. 左供52W, 右供78W. 3-6. 1; 1A; 0.75A.3-7. 3A; 1.33mA; 1.5mA; 2/3A; 2A. 3-8. 20V , –75.38V.3-9. –1A; 2A; –17.3mA. 3-10. 5V , 20; –2V, 4. 3-12. 4.6. 3-13. 2V; 0.5A. 3-14. 10V , 5k .3-15. 4/3, 75W; 4/3, 4.69W. 3-16. 1, 2.25W. 3-18. 50. 3-19. 0.2A. 3-20. 1A. 3-21. 1.6V . 3-22. 4A; –2A.3-23. 23.6V; 5A,10V . 3-24. 52V . ※第四章4-1. 141.1V , 100V , 50Hz, 0.02s,0o , –120o ; 120 o.4-2. 7.07/0 o A, 1/–45 o A, 18.75/–40.9 oA. 4-3. 3mU , 7.75mA .4-4. 10/53.13o A, 10/126.87o A, 10/–126.87oA,10/–53.13oA ；各瞬时表达式略。

第一章习题图示元件当时间t<2s时电流为2A，从a流向b；当t>2s时为3A，从b流向a。

根据图示参考方向，写出电流的数学表达式。

图示元件电压u=(5-9e-t/t)V，t>0。

分别求出t=0 和t→¥时电压u的代数值及其真实方向。

图题图题图示电路。

设元件A消耗功率为10W，求；设元件B消耗功率为-10W,求；设元件C发出功率为-10W，求。

图题求图示电路电流。

若只求，能否一步求得图示电路，已知部分电流值和部分电压值。

(1) 试求其余未知电流。

若少已知一个电流，能否求出全部未知电流(2) 试求其余未知电压u14、u15、u52、u53。

若少已知一个电压，能否求出全部未知电压图示电路，已知,,,。

求各元件消耗的功率。

图示电路，已知，。

求(a)、(b)两电路各电源发出的功率和电阻吸收的功率。

求图示电路电压。

求图示电路两个独立电源各自发出的功率。

求网络N吸收的功率和电流源发出的功率。

求图示电路两个独立电源各自发出的功率。

求图示电路两个受控源各自发出的功率。

图示电路，已知电流源发出的功率是12W，求r的值。

求图示电路受控源和独立源各自发出的功率。

图示电路为独立源、受控源和电阻组成的一端口。

试求出其端口特性，即关系。

讨论图示电路中开关S开闭对电路中各元件的电压、电流和功率的影响，加深对独立源特性的理解。

第二章习题图(a)电路，若使电流A,，求电阻；图(b)电路，若使电压U=(2/3)V，求电阻R。

求图示电路的电压及电流。

图示电路中要求，等效电阻。

求和的值。

求图示电路的电流I。

求图示电路的电压U。

求图示电路的等效电阻。

求图示电路的最简等效电源。

图题利用等效变换求图示电路的电流I。

(a) (b)图题求图示电路的等效电阻R。

求图示电路的电流和。

列写图示电路的支路电流方程。

图题图示电路，分别按图(a)、(b)规定的回路列出支路电流方程。

图题用回路电流法求图示电路的电流I。

用回路电流法求图示电路的电流I。

答案3.1解：应用置换定理，将电阻R 支路用0.5A I =电流源代替，电路如图电流源代替，电路如图(b)(b)(b)所示。

所示。

所示。

I2W 4-+UW1W 5.4V6W 3(b)0.5A ①②对电路列节点电压方程：对电路列节点电压方程：1212(1)0.5A 44n n I U U +W ´-=-W W12116V (1)3 4.5 4.5n n U U -+W ++´=W W W0.5A I = 解得解得11V n U = 则12n U R I==W 答案3.2解：解：（a ）本题考虑到电桥平衡，再利用叠加定理，计算非常简单。

（1）3V 电压源单独作用电压源单独作用,,如图如图(a-1)(a-1)(a-1)、、(a-2)(a-2)所示。

所示。

所示。

W 2W 6W 1W3W)3/1(V3'I '1I 8W4WW)3/1(V3'I '1I (a-1)(a-2)由图由图(a-2)(a-2)(a-2)可得可得可得'3V 1A 148348I ==´W +W + 由分流公式得：由分流公式得：''182A 483I IW =-´=-W +W （2）1A 电流源单独作用，如图电流源单独作用，如图(a-3)(a-3)(a-3)所示。

所示。

所示。

(a-3)W 2W 6W 1W3W)3/1("I "1IA1考虑到电桥平衡，考虑到电桥平衡， "0I =， 在由分流公式得：在由分流公式得： "1131A A 134I =-´=-+ （3）叠加：）叠加：'"1A I I I =+='"11117/12A I I I =+=-2111 2.007WP I W =´=（b ）（1）4V 电压源单独作用，如图电压源单独作用，如图(b-1)(b-1)(b-1)所示。

第一章习题图示元件当时间t<2s时电流为2A，从a流向b；当t>2s时为3A，从b流向a。

根据图示参考方向，写出电流的数学表达式。

图示元件电压u=(5-9e-t/t)V，t>0。

分别求出t=0 和t→¥时电压u的代数值及其真实方向。

图题图题图示电路。

设元件A消耗功率为10W，求；设元件B消耗功率为-10W,求；设元件C 发出功率为-10W，求。

图题求图示电路电流。

若只求，能否一步求得？图示电路，已知部分电流值和部分电压值。

(1) 试求其余未知电流。

若少已知一个电流，能否求出全部未知电流？(2) 试求其余未知电压u14、u15、u52、u53。

若少已知一个电压，能否求出全部未知电压？图示电路，已知,,,。

求各元件消耗的功率。

图示电路，已知，。

求(a)、(b)两电路各电源发出的功率和电阻吸收的功率。

求图示电路电压。

求图示电路两个独立电源各自发出的功率。

求网络N吸收的功率和电流源发出的功率。

求图示电路两个独立电源各自发出的功率。

求图示电路两个受控源各自发出的功率。

图示电路，已知电流源发出的功率是12W，求r的值。

求图示电路受控源和独立源各自发出的功率。

图示电路为独立源、受控源和电阻组成的一端口。

试求出其端口特性，即关系。

讨论图示电路中开关S开闭对电路中各元件的电压、电流和功率的影响，加深对独立源特性的理解。

第二章习题图(a)电路，若使电流A,，求电阻；图(b)电路，若使电压U=(2/3)V，求电阻R。

求图示电路的电压及电流。

图示电路中要求，等效电阻。

求和的值。

求图示电路的电流I。

求图示电路的电压U。

求图示电路的等效电阻。

求图示电路的最简等效电源。

图题利用等效变换求图示电路的电流I。

(a) (b)图题求图示电路的等效电阻R。

求图示电路的电流和。

列写图示电路的支路电流方程。

图题图示电路，分别按图(a)、(b)规定的回路列出支路电流方程。

图题用回路电流法求图示电路的电流I。

用回路电流法求图示电路的电流I。

电路理论基础课后答案(哈工大陈希有)第11章题11.1 根据定义求和的象函数。

解： (1)(2)题11.2设求的象函数。

解：由拉氏变换的微分、线性和积分性质得：题11.3设(t 为纯数)。

分别求对应象函数、、，验证卷积定理。

解：设 , 则与的卷积为)()(t t t f ε=)(e )(t t t f atε-=2020001e 1e 1e e )()(-ss dt s s t dt t t s F stst st st=-=+-==∞-∞-∞-∞----⎰⎰ε20)(20)(00)(1e )(1e 1e e )(e )(-ααααεααα+=+-=+++-==∞+-∞+-∞-∞-----⎰⎰s s dt s s t dt t t s F t s t s st st t ξξετd f c t bf tt f a t f f t A t f t t )()(d )(d )(,0)0(),()e 1()(011121/1⎰-++==-=--)(2t f )(2s F )/1(//1)(1τττ+=+-=s s A s A s A s F )/1(/)()()/(]/)([)()]0()([)(22111112ττ+++=++=++-=-s s A c bs as s F s c b as s s F c s bF f s sF a s F )()()(,e 2)(,e 5)(215221t f t f t f t f t f tt *===--)(1s F )(2s F )(s F 25)}({)(11+==s t f s F L 52)}({)(22+==s t f L s F )5)(2(10)()(21++=s s s F s F )(1t f )(2t f对上式取拉氏变换得：由此验证。

题11.4求下列函数的原函数。

(a) (b)(c)解：(a)， 所以(b)所以)e e (310]e 31[e 10e e 10e 2e 5)(*)(520350350)(5221tt t tt ttt d d t f t f --------=⨯==⨯=⎰⎰ξξξξξξ)5)(2(10)5121(310)}(*)({21++=+-+=s s s s t f t f L )()()}(*)({2121s F s F t f t f =L 6512)(2+++=s s s s F)2)(1(795)(23+++++=s s s s s s F 623)(2++=s s s F 6512)(2+++=s s s s F 3221+++=s A s A 3|31221-=++=-=s s s A 3|31221-=++=-=s s s A tt s s t f 321e 5e 3}3523{)(---+-=+++-=L )2)(1(795)(23+++++=s s s s s s F 212)2)(1(3221+++++=+++++=s A s A s s s s s 2|2311=++=-=s s s A 1|1321-=++=-=s s s A tt t t s s s L t f 21e e 2)(2)(}21122{)(----++'=+-++++=δδ(c)查表得题11.5分别求图示(a)、(b)电路的等效运算阻抗或等效运算导纳。