下载文档原格式
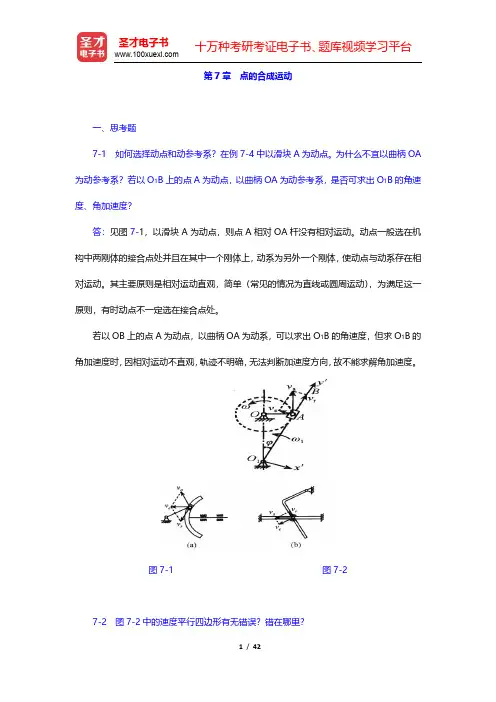
习 题7-1 如图7-26所示，光点M 沿y 轴作谐振动，其运动方程为：x = 0，)cos(θω+=t A y ，式中，A 、ω、θ均为常数。
如将点M 投影到感光记录纸上，此纸以等速v e 向左运动，试求点在记录纸上的轨迹。
图7-26t v x e =')cos()cos(eθωθω+'=+=='x v A t A y y7-2 用车刀切削工件的端面，车刀刀尖M 的运动方程为 t b x ωsin =，其中b 、ω为常数，工件以等角速度ω逆时针方向转动，如图7-27所示。
试求车刀在工件端面上切出的痕迹。
图7-27t b t y t x x ωωωsin sin cos ='-'= 0cos sin ='+'=t y t x y ωω 解得)2sin(2cos sin sin tan cos sin t b t t b t t t t b x ωωωωωωω==+=' ]1)2[cos(2sin tan 2-=-='-='t bt b t x y ωωω4)2()(222b b y x =+'+'7-3 河的两岸相互平行，如图7-28所示。
设各处河水流速均匀且不随时间改变。
一船由点A 朝与岸垂直的方向等速驶出，经过10 min 到达对岸，这时船到达点B 的下游120 m 处的点C 。
为使船A 能垂直到达对岸的点B ，船应逆流并保持与直线AB 成某一角度的方向航行。
在此情况下，船经12.5 min 到达对岸。
试求河宽L 、船相对于水的相对速度v r 和水的流速v 的大小。
图7-28m/s 2.0600120==v 600r L v =船A 能垂直到达对岸的点B750a L v = 2a22r v v v += 2222.0)750()600(+=L L m 200)7501()6001(2.022=-=L m/s 31r =v7-4 半径R = 60mm 的半圆管BC 绕定轴OO 1按规律)5(t t -=ϕ转动，点在管内运动，相对于管子的运动方程为2π10t BM =(弧长的单位为mm)，如图7-29所示。
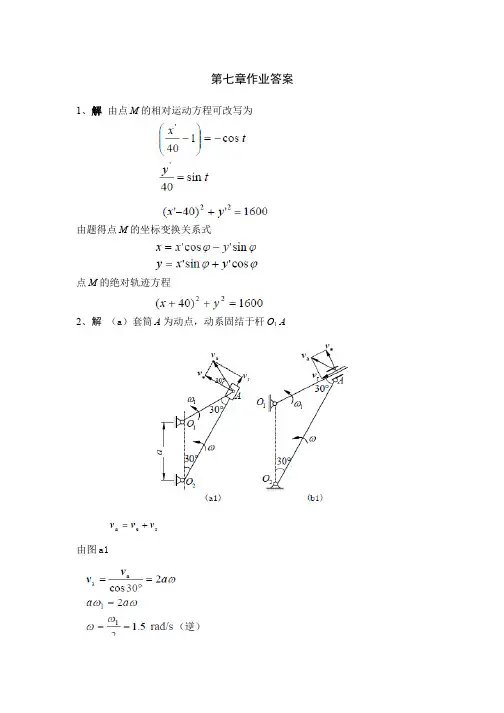
第七章作业答案1、解 由点M 的相对运动方程可改写为
由题得点M 的坐标变换关系式
点M 的绝对轨迹方程
2、解 （a）套筒A 为动点，动系固结于杆O1 A
由图a1
（b）套筒A 为动点，动系固结于杆O2 A，速度分析如图b1 所示。
3、解 ① 活动销子M 为动点，动系固结于轮O
② 活动销子M 为动点，动系固结于杆OA
速度分析如图b 所示
4、解 速度分析，如图b所示
加速度分析，如图c所示
5、解 点A 为动点，动系固结于小车，加速度分析如图b 所示。
由题意得t = 1 s时，各量为
分别向轴x ， y 方向投影得
6、解 小环M 为动点，动系固结于曲杆OBC，速度分析如图b 所示。
加速度分析如图c 所示。
第7章 点的合成运动一、是非题（正确的在括号内打“√”、错误的打“×”）1．点的速度和加速度合成定理建立了两个不同物体上两点之间的速度和加速度之间的 关系。
( √ ) 2．根据速度合成定理，动点的绝对速度一定大于其相对速度。
( × )3．应用速度合成定理，在选取动点和动系时，若动点是某刚体上的一点，则动系不可以固结在这个刚体上。
( √ )4．从地球上观察到的太阳轨迹与同时在月球上观察到的轨迹相同。
( × ) 5．在合成运动中，当牵连运动为转动时，科氏加速度一定不为零。
( × ) 6．科氏加速度是由于牵连运动改变了相对速度的方向而产生的加速度。
( √ ) 7．在图中，动点M 以常速度r v 相对圆盘在圆盘直径上运动，圆盘以匀角速度ω绕定轴O 转动，则无论动点运动到圆盘上的什么位置，其科氏加速度都相等。
( √ )二、填空题1．已知r 234=++v i j k ，e 63=-ωi k ，则k =a 18 i ＋ -60 j ＋ 36 k 。
2．在图中，两个机构的斜杆绕O 2的角速度均为2ω，O 1O 2的距离为l ，斜杆与竖直方向的夹角为θ，则图(a)中直杆的角速度=1ωθθωcos sin 2，图(b)中直杆的角速度=1ω2ω。
图 图3．科氏加速度为零的条件有：动参考系作平动、0=r v 和r e v ω//。
4．绝对运动和相对运动是指动点分别相对于定系和动系的运动，而牵连运动是指牵连点相对于定系的运动。
牵连点是指某瞬时动系上和动点相重合的点，相应的牵连速度和加速度是指牵连点相对于定系的速度和加速度。
5．如图所示的系统，以''Ax y 为动参考系，Ax'总在水平轴上运动，AB l =。
则点B 的相对轨迹是圆周，若kt ϕ= (k 为常量)，点B 的相对速度为lk ，相对加速度为2lk 。
图6．当点的绝对运动轨迹和相对运动轨迹都是曲线时，牵连运动是直线平动时的加速度合成定理表达式是a e r =+a a a ；牵连运动是曲线平动时的加速度合成定理表达式是 a e r =+a a a ；牵连运动是转动时的加速度合成定理表达式是a e r k =++a a a a 。
第七章点的合成运动习题解析［习题7-1］汽车A以V i 40km/h沿直线道路行驶，汽车B以V2 4O.._2km/h沿另一叉道行驶。
求在B车上观察到的A车的速度。
解：动点：A车。
动系：固连于B车的坐标系。
静系：固连地面的坐标系。
绝对运动：动点A相对于地面的运动。
相对运动：动点A相对于B车的运动。
牵连运动：在动系中，动点与动系的重合点，即牵连点相对于静系（地面）的运动。
当A、E两车相遇时，即它们之间的距离趋近于0时，A、E相重合，E车相对于地面的速度就是牵连速度。
V e V2。
由速度合成定理得：V V e V r。
用作图法求得：v r V AB 40km/ h （f）故，E车上的人观察到A车的速度为V r V AB［习题7-2］由西向东流的河，相对于水流的划速为1m/s。
问：（1）若划速保持与河岸垂直，船在北岸的何处靠岸？渡河时间需多久？（2）若欲使船在北岸上正对出发点处靠岸，划船时应取什么方向？渡河时间需多久？解：（1）动点：船。
动系：固连在流水上。
静系：固连在岸上。
绝对运动：岸上的人看到的船的运动。
相对运动：船上的有看到的船的运动。
牵连运动：与船相重合的水体的运动。
绝对速度：未知待求，如图所示的V。
相对速度：V r1m/s，方向如图所示。
牵连速度：V e 0.5m/s，方向如图所示。
由速度合成定理得：V V e V r 40km/h，方向如图所示。
宽1000m,流速为0.5m/s ,小船自南岸某点出发渡至北岸，设小船V rv .. V V -： 0.52 121.118(m/s)arcta n 土V e1 arcta n —— 0.5AC10001000500( m),即，船将在北岸下流5 0 0tan 2n 处靠岸。
如图所示，A 为出渡河所花的时间：t 11000m1000(s) 16 分 40 秒1m/ s发点，E 为靠岸点。
(2)• V e . 0.5 arcs in arcs inv r 1 v . v ； v ； 12 0.52即船头对准方向为北偏西 300 渡河所花的时间： t 2 1000 m 1155( s) 19 分 15秒0.866m/ s 300 0.866(m/s) ［习题7-3］播种机以匀速率 w 1m/s 直线前进。
种子脱离输种管时具有相对于输种管的速度 v ； 2m/s 。
求此时种子相对于地面的速度，及落至地面上的位置与离开输种管时的位置之间 水平距离。
解： 动点：种子。
动系：固连于输种管的坐标系。
静系：固连于地面的坐标系。
绝对速度：种子相对于地面的速度，未知待求。
相对速度：v r v 2 2m/ s 牵连速度：v e v 1 1m/s v v e 5 v 1222 2 1 2cos120° 2.65(m/s)63.435°2.65sin (60°) si n120°60° arcsin ——19.07°2.6540.930即v 与V i 之间的夹角为 40.930。
种子走过的水平距离为：s v x t vcos tvsin t 0.252.65sin40.930t 0.5 9.8t 24.9t 2 1.736t 0.25: 21.736 pi.7364 4.9 ( 0.25) 2 4.9s 2.65 cos 40.930 0.110.22(m)［习题7-4］砂石料从传送带A 落到另一传送带E 的绝对速度为 v 1 4m/ s ，其方向与铅直线成300角。
设传送带E 与水平面成 150角，其速度为V 2 2m/s ，求此时砂石料对于传送带E 的相对速度。
又当传送带E 的速度多大时，砂石料的相对速度才能与 B 带垂直。
解: 动点：砂石料。
动系：固连于传送带E 的坐标系。
静系：固连于地面的坐标系。
绝对速度：砂石料相对于地面的速度，v v 1 4m/s 。
相对速度：砂石料相对于传送带E 的速度，待求。
牵连速度：传送带E 相对于地面的速度：v e v 2 2m/s v a v e v rv r 22 42 2 2 4cos750 3.98(m/s)V y t 2gt1.7362.8139.80.11(s) 0.464(s)(不合舍去)当v r V B时，传送带E的速度为：v B v a sin15°4sin15° 1.04(m/s)［习题7-5］三角形凸轮沿水平方向运动，其斜边与水平线成置在斜面上，另一端E在气缸内滑动，如某瞬时凸轮以速度角。
杆AE的A端搁V向右运动，求活塞E的速度。
解：动点：A。
动系：固连于凸轮上的坐标系。
静系：固连于地面的坐标系。
绝对速度：A相对于地面的速度，待求。
相对速度：A相对于凸轮的速度。
牵连速度：凸轮相对于地面的速度。
V a V e V rv A vta n因为杆AE作上下平动，故活塞E的速度为:V a V AV e Vv B V A vta n［习题7-6］图示一曲柄滑道机构，长OA r的曲柄，以匀角速度绕O轴转动。
装在水平杆CE上的滑槽DE与水平线成600角。
求当曲柄与水平线的夹角分别为00、300、600时, 杆EC的速度。
解：动点：A。
动系：固连于CEDE 上的坐标系。
动系平动， V A V CBDE V BC静系：固连于地面的坐标系。
绝对速度：A 相对于地面的速度。
相对速度：A 相对于DE 的速度。
牵连速度：CEDE 相对于地面的速度。
V a V e V r V a rVBC r sin( 300)sin 1200sin(0 30 ) sin 1200负号表示此时速度方向与图示方向相反，即向左。
解： 动点：Co动系：固连于OC 杆上的坐标系。
静系：固连于地面的坐标系。
V BCsin (180°1200 90°)sin 120°V BCsin( 300) sin 1200..3 r3V BC 1 300sin (300 300)sin 1200 此时往复运动改变方向。
V BC | 60°sin (600 300) 0sin 12023 r[习题7-7] 摇杆OC 带动齿条AE 上下移动, 齿条又带动直径为10 0 mm 的齿轮绕O 1轴摆动。
在图所示瞬时，OC 之角速度3 0 = 0 . 5 ad/s ，求这时齿轮的角速度。
V BC 1绝对速度：C 相对于地面的速度。
相对速度：C 相对于OC 杆的速度。
牵连速度：OC 杆相对于地面的速度。
即齿轮的角速度为 1 5.33rad / s［习题7-8 ］摇杆滑道机构的曲柄OA 长 I , OAXOO - AB 2I ，求该瞬时EC 杆的速度。
解： 动点：A 。
动系：固连于O 1D 杆上的坐标系。
静系：固连于地面的坐标系。
绝对速度：A 相对于地面的速度， v a I 0。
相对速度：A 相对于 O i D 杆的速度。
V e OC 0.40.5 0.231(m/s)cos30V a V e V rV a V e0.2 0.267(m/s)cos30°2c c°cos 30V a V AB r 10.2/0.750.267/r 10.2/0.75 5.33(rad / s)1 0.05以匀角速度3。
绕O 轴转动。
已知在图所示位置牵连速度：OQ 杆相对于地面的速度。
V a V e VV eV a sin 300 丄I 02V e O 1A O] D2 02lO 1D10O 1D1 04动点: Bo动系：固连于O j D杆上的坐标系。
静系：固连于地面的坐标系。
绝对速度：E相对于地面的速度。
相对速度：E相对于O1D杆的速度。
牵连速度：O j D杆相对于地面的速度。
V a V e V rV-O1B O i D411 l1 0 4V a V e l 0 1.1551 0cos3000.866BC乍平动，故v BC v a 1.15510[习题7-9] —外形为半圆弧的凸轮A,半径r = 3 0 0 mm，沿水平方向向右作匀加速运动，2其加速度a A= 8 0 0 mm/s 。
凸轮推动直杆EC沿铅直导槽上下运动。
设在图所示瞬时,V A=6 0 0mm/s，求杆EC的速度及加速度。
解：动点：E。
动系：固连于凸轮A上的坐标系。
静系：固连于地面的坐标系。
绝对速度：E相对于地面的速度。
相对速度：E相对于凸轮的速度。
牵连速度：E相对于凸轮的速度。
V a V e V r凸轮在水平面上作平动，EC在铅垂方向上作平动。
V e V ABV BC V B V a V e COt30°V A cot30°600 3 1039.23(mm/s)V r - 0 2V e 2 600 1200(mm/s)sin 30nx a a a e a r a e a r a r上式在x轴上的投影为:a a cos60°a e cos300n ar2a r3a e2 V ra a 1.732r2(1200)800 2 -30028214.4(mm/s )，负号表示方向向下。
[习题7-10]铰接四边形机构中的O 1A = O 2E=100mm,O 1O2 = AE，杆O 1A以等角速度w=2r ad/s绕O i轴转动。
AE杆上有一套筒C, 此筒与CD杆相铰接，机构各部件都在同一铅直面内。
求当0 = 60 °时0。
杆的速度和加速度。
解：动点：c。
动系：固连于AE杆上的坐标系。
静系：固连于地面的坐标系。
绝对速度: C相对于地面的速度。
相对速度: C相对于AE杆的速度。
牵连速度: AE杆相对于地面的速度。
V a V e V rV e v A O1A 100 2 200(mm/s)V a 0v e cos60 200 0.5 100(mm/s) ea a a e a ra e a Aa e100(mm / s)a e na e2VO1AO1A 2100 22400(mm/s2)a a 0a e sin 60 400 0.866 346.4(mm/s2)a CD a C a a 346.4(mm/s)［习题7-11］具有圆弧形滑道的曲柄滑道机构，用来使滑道CD获得间歇往复运动。
若已知曲柄OA 作匀速转动，其转速为w = 4nrad/s ，又R = OA=100mm ，求当曲柄与水平 轴成角0 = 30°时滑道CD 的速度及加速度。
解: 动点：A 。
动系：固连于滑道CD 上的坐标系。
静系：固连于地面的坐标系。
绝对速度：A 相对于地面的速度。
相对速度：A 相对于滑道CD 的速度。
牵连速度：滑道CD 相对于地面的速度。
V a V e V r加速度在 方向的投影：a a cos60° a e cos30° a ；15.775 0.5 a e 0.866 15.775 2a e 27.32(m/s )2a CD a e 27.32(m/s )［习题7-12］销钉M 可同时在槽AB,CD 内滑动。
