下载文档原格式
8-4 点的加速度合成定理三种加速度(相对于三种运动,瞬时量)绝对加速度动点相对静系运动的加速度相对加速度动点相对动系运动的加速度牵连加速度牵连点的加速度8-4点的加速度合成定理a a r a e a动点--M 点定系--OXYZ动系--O ˊXˊYˊZˊ牵连点—动系O ˊXˊYˊZˊ上M 点M O r r r ''=+r x i y j z k '''''''=++为常矢量，，其中考虑到考虑到则M a O dr v r x i y j z k x i y j z k dt '''''''''''''==++++++eO O edv dv a a dt dt ''===r rr dv dv a dt dt==点的加速度合成定理—当牵连运动为平动时，动点在某瞬时的绝对加速度等于它在该瞬时的牵连加速度与相对加速度的矢量和。
2222222222o M a d r d r d x d y d z a i j k dt dt dt dt dt '''''''==+++a e r a a a =+上式中每一个矢量都有大小和方向两个要素，因此上式总共包含有12个要素，其中若仅有两个要素是未知的，则此矢量式可解。
由于加速度包括沿轨迹切线方向的切向加速度和沿主法线方向的法向加速度两个分量，所以在最一般的情况下练习1凸轮在水平面上向右作减速运动，如图所示。
设凸轮半v a径为R，图示瞬时的速度和加速度分别为和。
求杆AB在图示位置时的加速度。
解：取动点和动系动点：顶杆AB上的A点动系：固结凸轮上的参考系绝对运动：铅垂方向直线运动相对运动：半圆周运动牵连运动：水平直线平移8该瞬时杆AB 的速度方向向上练习1—速度分析绝对速度：大小未知，方向沿杆AB 向上牵连速度：，方向水平向右相对速度：大小未知，方向沿凸轮圆周的切线根据速度合成定理ϕϕsin sin e r vv v ==a v e v r v e v v =练习1—加速度分析绝对加速度：大小未知，方向沿直线AB 牵连加速度：，沿水平方向相对加速度法向分量：，沿着，指向半圆板圆心相对加速度切向分量：大小未知，垂直于，假设指向右下a a e a e a a OA OA O。
理论力学点的速度合成定理建立动点的绝对速度，相对速度和牵连速度之间的关系。
MM ' 绝对 绝对 M 1M ' 相对 M 1M ' 相对MM ' MM 1M 1M 't → t + t AB →A'B'M → M'成M →M →M∆t ，∆t →0 的 ，limM M '=limM M +limM M ∆t →0∆t →0∆t →0∆t∆t∆tv a =v e +v r即在任 瞬 动点的绝对速度等于其牵连速度与相对速度的矢量和，这就是点的速度合成定理。
v a —动点的绝对速度v r —动点的相对速度 v e —动点的牵连速度，是动系 点(牵连点)的速度动系 ，动系 点速度 相等; 动系 动 ，v e 是 瞬 动系 与动点相 合点的速度。
r M =r O '+r 'rr '=x 'i '+y 'j '+z 'k '(r M'r M =r M 'v r= d r '=d x 'i '+d y 'j '+d t d t d t v v r i ' j ' k 'e v =d r M '=d rO '+x 'd i '+y 'd j '+z d t d t d t d t a =v e +v r=d r O '+x 'd i '+y 'd j '+z 'd k '+d x 'i '+d y 'j '+d z 'k 'd t d t d t d t d t d t d t =d r M d tv v eM' x' y' z'v a点的速度合成定理是瞬 矢量 ，共包括大小‚方向 六个元素，已知任意四个元素，就能求出其他 个。
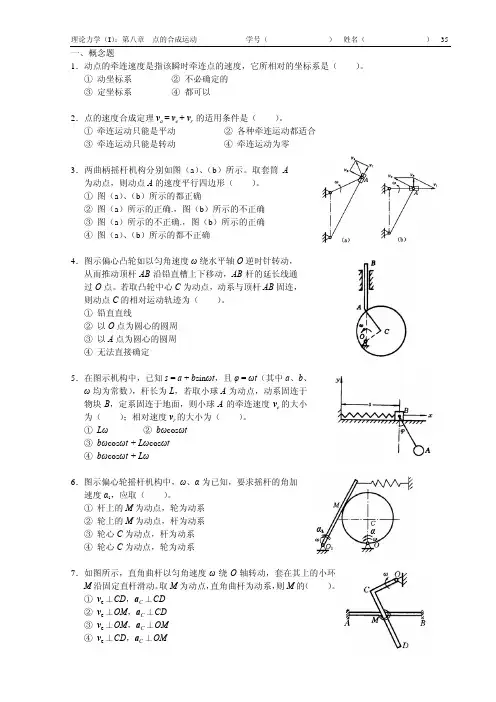
一、概念题1．动点的牵连速度是指该瞬时牵连点的速度，它所相对的坐标系是（ ）。
① 动坐标系 ② 不必确定的③ 定坐标系 ④ 都可以2．点的速度合成定理v a = v e + v r 的适用条件是（ ）。
① 牵连运动只能是平动 ② 各种牵连运动都适合③ 牵连运动只能是转动 ④ 牵连运动为零3．两曲柄摇杆机构分别如图（a ）、（b ）所示。
取套筒A为动点，则动点A 的速度平行四边形（ ）。
① 图（a ）、（b ）所示的都正确② 图（a ）所示的正确.，图（b ）所示的不正确③ 图（a ）所示的不正确.，图（b ）所示的正确④ 图（a ）、（b ）所示的都不正确4．图示偏心凸轮如以匀角速度ω绕水平轴O 逆时针转动，从而推动顶杆AB 沿铅直槽上下移动，AB 杆的延长线通过O 点。
若取凸轮中心C 为动点，动系与顶杆AB 固连，则动点C 的相对运动轨迹为（ ）。
① 铅直直线② 以O 点为圆心的圆周③ 以A 点为圆心的圆周④ 无法直接确定5．在图示机构中，已知s = a + b sin ωt ，且φ = ωt （其中a 、b 、ω均为常数），杆长为L ，若取小球A 为动点，动系固连于物块B ，定系固连于地面，则小球A 的牵连速度v e 的大小为（ ）；相对速度v r 的大小为（ ）。
① L ω ② b ωcos ωt③ b ωcos ωt + L ωcos ωt④ b ωcos ωt + L ω6．图示偏心轮摇杆机构中，ω、α为已知，要求摇杆的角加速度α1，应取（ ）。
① 杆上的M 为动点，轮为动系② 轮上的M 为动点，杆为动系 ③ 轮心C 为动点，杆为动系④ 轮心C 为动点，轮为动系7．如图所示，直角曲杆以匀角速度ω绕O 轴转动，套在其上的小环M 沿固定直杆滑动。
取M 为动点，直角曲杆为动系，则M 的（ ）。
① v e ⊥CD ，a C ⊥CD② v e ⊥OM ，a C ⊥CD③ v e ⊥OM ，a C ⊥OMα α18．平行四边形机构如图。
点的合成运动中动点＼动系的选取原则和方法摘要系统阐述点的合成运动中动点、动系的四条选取原则及各类问题中动点和动系的选取方法,并列举实例加以分析说明。
关键词合成运动;动点;动系;选择点的合成运动是理论力学的运动学部分的重点,同时也是难点,对初学的大学生和部分青年教师来讲,都是不太容易理解和掌握的。
在合成运动理论中,首先要选定一个动点,它可以是抽象为点的刚体,也可以是运动刚体上的某一确定点。
然后选定两个坐标系:定系和动系,通常把固结在地球上的坐标系选为定系,固结在其他相对于地球运动的参考体上的坐标系选为动系。
最后再分析三种运动:绝对运动、相对运动和牵连运动。
这其中,选取合适的动点、动系最为关键,它是解题技巧中最重要的,也是难以确定的。
动点、动系选择得合适,三种运动分析就很简单,速度分析和加速度分析也就顺理成章。
选取动点、动系一般应遵循如下四条原则:1)动点与动系不能选在同一物体上。
动点相对于动系是运动的,若选在同一物体上,就没有相对运动。
2)动系固结在相对于定系运动的物体上。
3)动点的相对运动轨迹要清楚,容易判断,从而便于确定相对速度和相对加速度的方位。
4)动点在运动过程中必须是系统中同一个确定的点。
它可以是抽象为点的刚体,也可以是运动刚体上的某一确定点。
下面针对几种不同问题,归纳出动点、动系的选取方法,并列举实例加以分析说明。
学生只要记住这些机构的特点和相应的动点、动系的选择方法,并针对具体题目应用即可。
1两物体之间通过小圆环相互连接可选小圆环为动点,动系固结在其中一运动物体上。
图1 图2如图1所示的运动机构中,小环M套在直杆OA与直角曲杆OBC上。
选小环M为动点,动系固结在绕O轴转动的直角曲杆OBC上,注意动系不能选在OA 杆上,因为OA杆相对地面不动。
则绝对运动为沿OA的直线运动,相对运动为沿BC的直线运动,牵连运动为杆OBC的定轴转动。
速度分析如图所示。
2运动机构中的不同情况一杆状构件(甲)的一端始终与另一物体(乙)的轮廓相接触。
