理论力学：第6章 点的合成运动

8-4 点的加速度合成定理三种加速度(相对于三种运动,瞬时量)绝对加速度动点相对静系运动的加速度相对加速度动点相对动系运动的加速度牵连加速度牵连点的加速度8-4点的加速度合成定理a a r a e a动点--M 点定系--OXYZ动系--O ˊXˊYˊZˊ牵连点—动系O ˊXˊYˊZˊ上M 点M O r r r ''=+r x i y j z k '''''''=++为常矢量，，其中考虑到考虑到则M a O dr v r x i y j z k x i y j z k dt '''''''''''''==++++++eO O edv dv a a dt dt ''===r rr dv dv a dt dt==点的加速度合成定理—当牵连运动为平动时，动点在某瞬时的绝对加速度等于它在该瞬时的牵连加速度与相对加速度的矢量和。

2222222222o M a d r d r d x d y d z a i j k dt dt dt dt dt '''''''==+++a e r a a a =+上式中每一个矢量都有大小和方向两个要素，因此上式总共包含有12个要素，其中若仅有两个要素是未知的，则此矢量式可解。

由于加速度包括沿轨迹切线方向的切向加速度和沿主法线方向的法向加速度两个分量，所以在最一般的情况下练习1凸轮在水平面上向右作减速运动，如图所示。

设凸轮半v a径为R，图示瞬时的速度和加速度分别为和。

求杆AB在图示位置时的加速度。

解：取动点和动系动点：顶杆AB上的A点动系：固结凸轮上的参考系绝对运动：铅垂方向直线运动相对运动：半圆周运动牵连运动：水平直线平移8该瞬时杆AB 的速度方向向上练习1—速度分析绝对速度：大小未知，方向沿杆AB 向上牵连速度：，方向水平向右相对速度：大小未知，方向沿凸轮圆周的切线根据速度合成定理ϕϕsin sin e r vv v ==a v e v r v e v v =练习1—加速度分析绝对加速度：大小未知，方向沿直线AB 牵连加速度：，沿水平方向相对加速度法向分量：，沿着，指向半圆板圆心相对加速度切向分量：大小未知，垂直于，假设指向右下a a e a e a a OA OA O。

论点的复合运动中动点、动系的选择原则和方法1引言理论力学是机械、土木类专业的专业基础课。

包括静力学、运动学和动力学三大部分。

运动学是从几何角度研究物体运动轨迹、运动方程、速度和加速度，而不考虑引起物体运动的物理原因。

其中点的合成运动是运动学的重点内容。

此部分内容题目多样，解题方法灵活，并且具有趣味性，完成一道题目时很有成就感。

当然也是让学生感到没有思路、无从下手的部分，普遍反映难度较大，也是测验、考核过程中丢分比较多的部分，问题的关键是无法正确的选取动点和动系。

本文从典型例题出发，介绍了点的合成运动中动点和动系的选取原则，可以帮助学生理清思路，提高点的合成运动的解题能力。

2点的合成运动概述在日常生活中，会经常遇到这样的情况。

当我们站在不同的参考物上，观察同一个物体的运动，发现物体所呈现的运动形式是不一样的。

举个最常见的例子，如图1。

人站在一辆沿直线匀速行驶的公共汽车上，以地面为参考物，观察人的运动，人在作匀速直线运动。

而以公共汽车为参考物，则人静止的。

可见，人的运动形式依选取的参考物不同而不同。

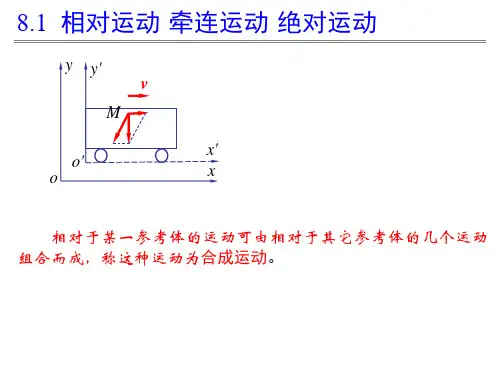
再引申一个例子，如图2。

沿直线轨道滚动的车轮，研究其轮缘上任意一点M的运动。

对于地面来说，点M的轨迹是旋轮线，而对于车厢来说，点M的轨迹则是一个圆。

车轮上的点M是沿旋轮线运动，是一种比较复杂复杂的运动形式，但是以车厢作为参考体，则点M相对于车厢的运动是简单的定轴转动，车厢相对于地面的运动是简单的平移。

轮缘上一点M的运动就可以看成为两个简单运动的合成，即点M相对于车厢作圆周运动，同时车厢相对地面作平移。

于是得到了合成运动的定义，即相对于某一参考体的运动可由相对于其他参考体的几个运动组合而成，称这种运动为合成运动。

3一点二系三运动研究点的合成运动，确定一个动点，选择定参考系和动参考系两个坐标系，分析动点的绝对运动、相对运动和牵连运动是首要任务。

3.1两个参考坐标系研究点的合成运动，总要涉及两个参考坐标系。

（1）定参考系建立在固定参考物上的坐标系，简称定系。

速度基点法和点的合成运动求速度法的比较
关于理论力学，用点的合成定理求加速度和用基点法求点的加速度的区别
关于理论力学，用点的合成定理求加速度和用基点法求点的加速度的区别我能不能认为，合成定理（可能存在科氏加速度）适用于2个刚体系统，而基点法只适用于一个刚体计算加速度？
对于刚体的平动,在同一个刚体上的就要用基点法,如果有套筒在一个转动的杆上相对运动这类情况,能够比较明显的判断出相对运动,绝对运动,牵连运动这三种运动,那就是用点的运动合成,多做一些题就可以分清楚了.
理论力学中点的合成理论与基点法求速度是一个方法吗
方法很相似：
速度：都有绝对速度v、相对速度vr、牵连速度ve物理量
加速度：都有绝对加速度a、相对加速度ar、牵连加速度ae物理量
不同的是：
前者动系、动点分别在两个物体上；
基点法求速度是对做刚体平面运动的物体而言的，动系、动点在同一个物体上。

求速度不仅可用基点法，还可用速度瞬心法和速度投影法。

求加速度基本都用基点f法。

2014级理论力学期末考试试题题库理论力学试题第一章物系受力分析画图题1、2、3、4、5、第二章平面汇交力系计算题1、2、3、4、5、6、7、第三章平面任意力系计算题2、4、5、7、8、第四章空间力系计算题1、2、3、4、5、6、第五章静力学综合填空题1、作用在刚体上某点的力，可以沿着其作用线移动到刚体上任意一点，并不改变它对刚体的作用效果。

2、光滑面约束反力方向沿接触面公法线指向被约束物体。

3、光滑铰链、中间铰链有1个方向无法确定的约束反力,通常简化为方向确定的 2 个反力。

4、只受两个力作用而处于平衡的刚体，叫二力构件,反力方向沿二力作用点连线。

5、约束力的方向与该约束所能阻碍的位移方向相反 .6、柔软绳索约束反力方向沿绳索 ,指向背离被约束物体.7、在平面只要保持力偶矩和转动方向不变，可以同时改变力偶中力的大小和力臂的长短，则力偶对刚体的作用效果不变。

8、力偶的两个力在任一坐标轴上投影的代数和等于零，它对平面的任一点的矩等于力偶矩，力偶矩与矩心的位置无关。

9、同一平面的两个力偶,只要力偶矩相等,则两力偶彼此等效.10、平面汇交力系可简化为一合力 ,其大小和方向等于各个力的矢量和,作用线通过汇交点.11、平面汇交力系是指力作用线在同一平面 ,且汇交与一点的力系.12、空间平行力系共有 3 个独立的平衡方程.13、空间力偶对刚体的作用效果决定于力偶矩大小、力偶作用面方位、力偶的转向三个因素。

14、空间任意力系有 6 个独立的平衡方程.15、空间汇交力系的合力等于各分力的矢量和,合力的作用线通过汇交点 . 第五章静力学综合摩擦填空题1、当作用在物体上的全部主动力的合力作用线与接触面法线间的夹角小于摩擦角时，不论该合力大小如何，物体总是处于平衡状态，这种现象称为自锁现象.2、答案：50N3、答案：φm/24、静摩擦力Fs的方向与接触面间相对滑动趋势的方向相反，其值满足__0<=F S<=F MAX摩擦现象分为滑动摩擦和__滚动摩阻__两类。

§6.2 平面运动刚体上点的速度1 基点法任何平面图形的运动都可视为随同基点的平移和绕基点转动的合成运动。

随着平面图形运动的分解与合成，图形上任一点的运动也相应地分解与合成。

应用点的合成运动的方法，便可求出图形上任一点的速度。

如图6-6所示，设某一瞬时图形上A 点的速度v A ，图形的角速度为ω。

若选A 点为基点，则根据点的速度合成定理，图形上任一点B 的绝对速度为v (6.2.1) r e v v +=B 由于牵连运动为动坐标系随同基点的平移，故牵连速度v e =v A 。

相对运动为图形绕基点A 的转动，即图形上各点以基点A 为中心作圆周运动，故相对速度为以AB 为半径绕A 点作圆周运动时的速度，记为v BA ，其大小为v BA =AB ⋅ω，方向垂直于AB ，指向与图形的转动方向一致。

B 点的速度可表示为v (6.2.2) BA A B v v +=即平面图形内任一点的速度，等于基点速度与该点绕基点转动速度的矢量和。

基于该结论计算平面图形内任一点速度的方法称为基点法。

例6.2-1图图6-6 平面运动刚体上点的速度的合成在应用时，应该注意到式(6.2.2)是一个矢量表达式，各矢量均有大小和方向两个要素，式中共有六个要素。

由于相对速度的方向总是已知的，它垂直于线段AB 。

因此还应知道另外三个要素，方可求解剩余的两个要素。

特别是若已知或求得平面图形角速度，以点A 为基点，用式(6.2.2)可求出图形上任意点的速度。

此外，应用式(6.2.2)作速度平行四边形时，必须注意应为速度平行四边形的对角线。

BA v B v 例6.2-1：曲柄滑块机构如图所示。

曲柄OA =20cm ，绕O 轴以等角速度ω0=10rad/s 转动，连杆AB =100cm 。

当曲柄与连杆相互垂直并与水平线间各成α=45°和β=45°时，求滑块B 的速度和AB 杆的角速度。

解：曲柄OA 作定轴转动，连杆AB 作平面运动，滑块B 作平移。

理论力学重难点及相应题解(总11页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除运动学部分：一、点的运动学重点难点分析1．重点：点的运动的基本概念（速度与加速度，切向加速度和法向加速度的物理意义等）；选择坐标系，建立运动方程，求速度、加速度。

求点的运动轨迹。

2．难点：运动方程的建立。

解题指导：1．第一类问题（求导）：建立运动方程然后求导。

若已知点的运动轨迹，且方程易于写出时，一般用自然法，否则用直角坐标法。

根据点的运动性质选取相应的坐标系，对于自然法要确定坐标原点和正向。

不管用哪种方法，注意将点置于一般位置，而不能置于特殊位置。

根据运动条件和几何关系把点的坐标表示为与时间有关的几何参数的函数，即可得点的运动方程。

2．第二类问题（积分）：由加速度和初始条件求运动方程，即积分并确定积分常数。

二、刚体的简单运动重点难点分析：1．重点：刚体平移、定轴转动基本概念；刚体运动方程，刚体上任一点的速度和加速度。

2．难点：曲线平移。

解题指导：首先正确判断刚体运动的性质。

其后的分析与点的运动分析一样分两类问题进行。

建立刚体运动方程时，应将刚体置于一般位置。

三、点的合成运动（重要）重点难点分析：1．重点：动点和动系的选择；三种运动的分析。

速度合成与加速度合成定理的运用。

2．难点：动点和动系的选择。

解题指导：1．动点的选择、动系的确定和三种运动的分析常常是同时进行的，不可能按顺序完全分开。

2．常见的运动学问题中动点和动系的选择大致可分以下五类：（1）两个（或多个）不坟大小的物体独立运动，（如飞机、海上的船舶等）对该类问题，可根据情况任选一个物体为动点，而将动系建立在另一个物体上。

由于不考虑物体的大小，因此动系（刚体）与物体（点）只在一个点上连接，可视为铰接，建立的是平移动坐标系。

（2）一个小物体（点）相对一个大物体（刚体）运动，此时选小物体为动点，动系建立在大物体上。