第八章 渐进法及超静定力的影响线.

第八章力法本章主要内容1）超静定结构的超静定次数2）力法的解题思路和力法典型方程（显然力法方程中所有的系数和自由项都是指静定基本结构的位移，可以由上一章的求位移方法求出（图乘或积分））3）力法的解题步骤以及用于求解超静定梁刚架桁架组合结构（排架）4）力法的对称性利用问题，对称结构的有关概念四点结论5）超静定结构的位移计算和最后内力图的校核6）§8-1超静定结构概述一、静力解答特征：静定结构：由平衡条件求出支反力及内力；超静定结构的静力特征是具有多余力，仅由静力平衡条件无法求出它的全部（有时部分可求）反力及内力，须借助位移条件（补充方程，解答的唯一性定理）。

二、几何组成特征：（结合例题说明）静定结构：无多余联系的几何不变体超静定结构：去掉其某一个或某几个联系（内或外），仍然可以是一个几何不变体系，如桁架。

即：超静定结构的组成特征是其具有多余联系，多余联系可以是外部的，也可能是内部的，去掉后不改变几何不变性。

多余联系（约束）：并不是没有用的，在结构作用或调整结构的内力、位移时需要的，减小弯矩及位移，便于应力分布均匀。

多余求知力：多余联系中产生的力称为三、超静定结构的类型（五种）超静定梁、超静定刚刚架、超静定桁架、超静定拱、超静定组合结构四、超静定结构的解法综合考虑三个方面的条件：1、平衡条件：即结构的整体及任何一部分的受力状态都应满足平衡方程；2、几何条件：也称变形条件、位移条件、协调条件、相容条件等。

即结构的变形必须符合支承约束条件（边界条件）和各部分之间的变形连续条件。

3、物理条件：即变形或位移与内力之间的物理关系。

精确方法：力法（柔度法）：以多余未知力为基本未知量位移法（刚度法）：以位移为基本未知量。

力法与位移法的联合应用：力法与位移法的混合使用：混合法近似方法：力矩分配法、矩阵位移法、分层总和法、D值法、反弯点法等本章主要讲力法。

五、力法的解题思路（结合例子）把不会算的超静定结构通过会算的基本结构来计算。

第八章渐进法和力矩分配法超静定结构的计算方法: 力法(六)、位移法（七）力法计算步骤1、选取基本体系2、列力法方程3、计算系数及自由项4、解方程5、作内力图位移法计算步骤1、设基本未知量2、列杆端弯矩方程3、列位移法方程4、解方程5、求杆端弯矩6、做内力图为避免解力法和位移法方程，引入一种近似的计算方法，这种方法是位移法的延伸，在计算过程中进行力矩的分配与传递。

渐近法有力矩分配法、无剪力分配法等，它们都是位移法的变体，其共同的特点是避免了组成和解算典型方程，也不需要计算结点位移，而是以逐次渐近的方法来计算杆端弯矩，计算结果的精度随计算轮次的增加而提高，最后收敛于精确解。

力矩分配法适用于连续梁和无结点线位移的刚架；无剪力分配法适用于刚架中除杆端无相对线位移的杆件外，其余杆件都是剪力静定杆件的情况，它是力矩分配法的一种特殊的形式。

对于一般有结点线位移的刚架，可用力矩分配法和位移法联合求解。

§8.1 力矩分配法的基本概念力矩分配法：理论基础：位移法；计算对象：杆端弯矩；计算方法：逐渐逼近的方法；适用范围：连续梁和无侧移刚架。

基本概念转动刚度S分配系数μ传递系数 C力矩分配法中符号规定力矩分配法的理论基础是位移法，故力矩分配法中对杆端转角、弯矩及固端弯矩的正负号规定与位移法相同，即都假设对杆端顺时针旋转为正号、对结点或附加刚臂逆时针旋转为正号。

一、转动刚度S：表示杆端对转动的抵抗能力。

在数值等于使杆端产生单位转角时需要施加的力矩。

转动刚度SAB 与杆的线刚度i （材料的性质、横截面的形状和尺寸、杆长）及远端支承有关，而与近端支承无关。

二、分配系数设A 点有力矩M ，求M AB 、M AC 和M AD如用位移法求解：A AB A AB AB S i M θθ==4A AC A AC AC S i M θθ==A AD A AD AD S i M θθ==30=∑AM A AD AC ABS S SM θ)(++=∑=++=AAD AC AB A SMS S S M θ所以有M SS M AABAB ∑=M S S M AAC AC ∑= M S S M AAD AD ∑=M M Aj Aj ⋅=μ ∑=AAjAj SS μ 1=∑μ三、传递系数=远端弯矩/近端弯矩M AB = 4 i ABθAM BA = 2 i ABθA在结点上的外力矩按各杆分配系数分配给各杆近端截面，各杆远端弯矩分别等于各杆近端弯矩乘以传递系数。

第8章渐近法及其他算法简述8.1 复习笔记本章介绍了几种属于位移法类型的渐近方法。

这些渐近方法的基础是力矩分配法，在力矩分配法的基础上，衍生出了适用于不同结构类型的子方法，如无剪力分配法、分层计算法、反弯点法。

渐近法舍弃了一部分精度，但以此换来了更高的效率。

一、力矩分配法的基本概念（见表8-1-1）1．转动刚度、分配系数、传递系数表8-1-1 力矩分配法的基本概念2．基本运算环节（单结点转动的力矩分配）（见表8-1-2）表8-1-2 单结点转动的力矩分配图8-1-1图8-1-2二、多结点的力矩分配（见表8-1-3）表8-1-3 多结点的力矩分配图8-1-3三、无剪力分配法（表8-1-4）表8-1-4 无剪力分配法图8-1-4四、近似法（见表8-1-5）表8-1-5 近似法图8-1-5 分层法五、超静定结构各类解法的比较和合理选用（见表8-1-6）表8-1-6 超静定结构各类解法的比较和合理选用8.2 课后习题详解8-1 试用力矩分配法计算图8-2-1所示结构，并作M图。

图8-2-1解：（a）求固端弯矩M AB F＝－F P l/8＝－20kN·m，M BA F＝F P l/8＝20kN·m求分配系数μBA＝EI/（EI＋EI/2）＝1/（1＋1/2）＝0.667，μBC＝（EI/2）/（EI＋EI/2）＝（1/2）/（1＋1/2）＝0.333放松B点进行力矩分配（B点的集中力偶应该与固端弯矩一起分配），分配过程如图8-2-2所示，并作出M图如图8-2-2所示。

图8-2-2（b）考虑去掉悬臂部分CD，去掉后在C点施加大小为10kN·m的顺时针力偶矩。

求固端弯矩（注意，C点的附加力偶传递到B点的作用不能忽略）M BC F′＝－3F P l/16＝－18kN·m（集中力引起）M BC F″＝1/2×10kN·m＝5kN·m（附加力偶引起）M BC F＝M BC F′＋M BC F″＝－13kN·m，M CB F＝10kN·m。

第8章 影响线及其应用小结一、影响线的概念当一个方向不变的单位集中荷载(P=1)在结构上移动时，表示结构某指定处的某一量值(支反力、剪力、轴力、弯矩、位移等)变化规律的图形，称为该量值的影响线。

要注意它和内力图的区别。

内力图是表示在固定荷载作用下，各截面内力分布规律的图形。

由于单位移动荷载(P=1)是无量纲的，因此，某量值影响线纵标的量纲=该量值的量纲/力的量纲。

例如，反力、剪力、轴力影响线纵标无量纲，弯矩和线位移影响线纵标的量纲分别为[长度]和[长度]／［力］)。

影响线的正负号规定如下：反力以向上为正，轴力以拉力为正，剪力以使隔离体有顺时针转动趋势为正，弯矩使梁下边纤维受拉为正；与上述情形相反则为负。

正影响线纵标绘在基线上方，负的绘在下方，并标注“+”、“—”号。

二、影响线的作法1．用静力法或机动法作静定结构的影响线 (1)静力法静力法是指用静力计算方法求某量值的影响线方程，然后再根据方程绘出图形。

其步骤如下：1)选取坐标原点，将P=1放在任意位置，以变量x 表示P=1作用点的位置； 2)取隔离体，建立平衡方程，求出某量值与x 之间的函数关系，即影响线方程； 3)根据影响线方程绘出图形，即影响线。

(2)机动法机动法是利用虚功原理作影响线。

作某量值Z 的影响线时，要撤去与量值Z 相应的约束，形成一个机构。

令机构沿S 正向产生单位虚位移1Z δ=，则荷载作用点的竖向位移图()p x δ即为量值Z 的影响线。

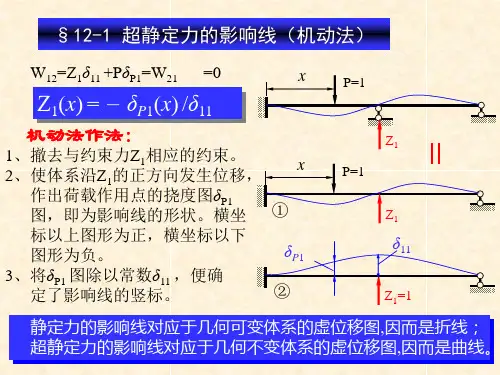
由虚功原理可得 ()()p Z x x δ=2．超静定力的影响线超静定力的影响线可用力法或位移法，力矩分配法直接求出，这也属于静力法。

另一种方法是利用超静定影响线与挠度图的比例关系作出影响线的大致形状，这相当于机动法。

超静定力影响线属于一般了解的内容。

三、影响线的应用1．利用影响线求各种荷载作用下的影响(1)集中荷载作用设集中荷载组P 1，P 2，…P n 作用点处某量值Z 的影响线纵标为y l ，y 2，…y n 则由之产生的总影响量为iiZ P y =∑(2)分布荷载作用当变化规律为已知的分布荷载q(x)作用于某确定位置时，由之产生的影响量为()()b aZ q x y x dx=⎰，式中，y 为影响线的纵标，积分的上、下限视q(x)的分布范围而定。

第八章渐进法及超铮定力的影响线（判断题）1、对只有一个刚结点的单结点结构，用力矩分配法计算的结果是精确解。

（）2、在多结点力矩分配过程中可以同时放松所有互不相邻的结点。

（）3、用力矩分配法对结构计算时，若计算过程中有错误，结果也能满足平衡条件，因此计算结果是否正确无法判别。

（）4、对图示结构的杆端B,其远端为固定端A,则其转动刚度S BA=4L（）4A B5、图（a）和（b）图所示单跨梁的A端转动刚度相同（）⑷（b）h~~-~⅛~■~rfI -- -- 1I ------ L-- 16、在图示连续梁中，杆端B的分配弯矩MBA=〃BA（-M B）。

（）8、图示结构各杆的长度和弯曲刚度相同，因此杆端弯矩MA*Mκ=Mιo=〃力。

（）9、力矩分配法不能计算有线位移的结构，但若结构中支座C有已知沉降Ac,则仍可用力矩分配法进行内力计算（如图）。

（）10、力矩分配法仅适用于解无线位移未知量的结构。

（）11、在力矩分配法中，同一刚性结点处各杆端的力矩分配系数之和等于1。

（）12、力矩分配法是一种逐次修正的方法。

（）13、图示结构中，若已知分配系数ABA=3/4,〃BA=1/4及力偶荷载Λ∕=60kN∙m则杆端弯矩M BA二-45kN∙m,M BC=T5kN∙m°（）14、图示结构的固端弯矩MABF=-6kN∙m.（15、图a和图b两个梁仅左端支座不一样，使它们左端产生相同转角所需施加的力矩是相等的。

（）16、力矩分配法中的分配系数、传递系数与外来因素（荷教、温度变化等）有关。

（）17、力矩分配法中的传递系数等于传递弯矩与分配弯矩之比，它与外因无关。

（）18、力矩分配法经过一个循环计算后，分配过程中的不平衡力矩（约束力矩）是传递弯矩的代数和。

（）19、图示刚架可利用力矩分配法求解。

（）20、力矩分配法计算荷教作用问题时，结点最初的不平衡力矩（约束力矩）仅是交于结点各杆端固端弯矩的代数和。

（）21、图示杆A8与CO的E/,/相等，但A端的转动刚度SAB大于C端的转动刚度SCD。