当前位置：文档之家 › 分波阵面干涉

分波阵面干涉

  • 格式：ppt
  • 大小：441.50 KB
  • 文档页数：9

下载文档原格式

  / 9

合集下载

分波面法双光束干涉

分波面法双光束干涉

求 (1) d =1.0 mm 和 d =10 mm两种情况下，相邻明条纹间距分 别为多大？(2) 若相邻条纹的最小分辨距离为 0.065 mm， 能分清干涉条纹的双缝间距 d 最大是多少？
解 (1) 明纹间距分别为
x D 600 5.893104 0.35mm
d
1.0
x D 600 5.893104 0.035mm
x D
d
一系列平行的 明暗相间条纹
(2) 已知 d , D 及Δx,可测 ；
(3) Δx 正比于 和 D ，反比于 d ；
(4) 当用白光作为光源时，在零级白色中央条纹两边对称地 排列着几条彩色条纹。
5
2021/3/11
红光入射的杨氏双缝干涉照片
白光入射的杨氏双缝干涉照片
6
2021/3/11
您能判断0级 条纹在哪吗？
§19.2 分波面法双光束干涉 一、杨氏实验 二、其他类似装置
干涉主要包含以下几个主要问题
•实验装置；
•确定相干光束，求出光程差(相位差)；
•分析干涉花样，给出强度分布； •应用及其他。
杨(T.Young)在1801 年首先发现光的干涉
现象，并首次测量了
1
2021/3/11
光波的波长。
一、 分波阵面法（杨氏实验)
1. 实验装置 ( 点源 分波面 相遇)
s1
S
s2
2. 强度分布 步骤
2
2021/3/11
明条纹位置
明条纹位置
明条纹位置
确定相干光束 计算光程差 根据相长、相消条件确定坐标
•理论分析
r12
D2
y2
(x
d )2 2
S2 •
r22

双棱镜干涉

双棱镜干涉

双棱镜干涉菲涅耳双棱镜实验是一种分波阵面的干涉实验，实验装置简单，但设计思想巧妙。

它通过测量毫米量级的长度，可以推算出小于微米量级的光波波长。

1881年菲涅耳用双棱镜实验和双面镜实验再次证明了光的波动性质，为波动光学奠定了坚实的基础 一、实验目的1. 观察双棱镜产生的双光束干涉现象，进一步理解产生干涉的条件；2. 学会用双棱镜测定光波波长。

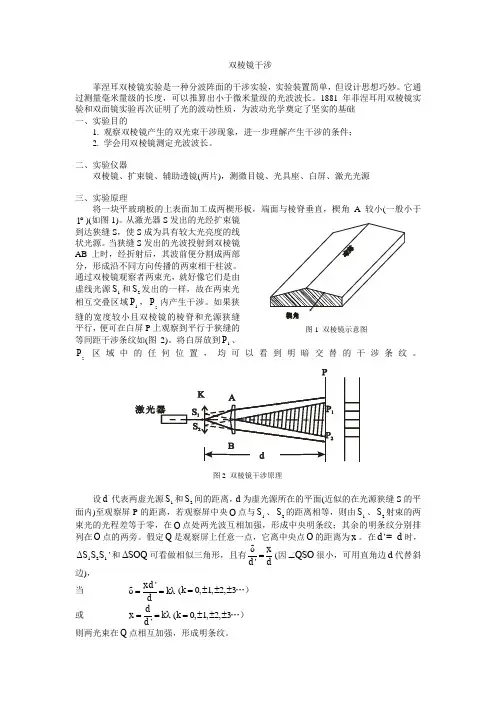
二、实验仪器双棱镜、扩束镜、辅助透镜(两片)，测微目镜、光具座、白屏、激光光源三、实验原理将一块平玻璃板的上表面加工成两楔形板，端面与棱脊垂直，楔角A 较小(一般小于1︒)(如图1)。

从激光器S 发出的光经扩束镜到达狭缝S ，使S 成为具有较大光亮度的线状光源。

当狭缝S 发出的光波投射到双棱镜AB 上时，经折射后，其波前便分割成两部分，形成沿不同方向传播的两束相干柱波。

通过双棱镜观察者两束光，就好像它们是由虚线光源1S 和2S 发出的一样，故在两束光相互交叠区域1P ，2P 内产生干涉。

如果狭缝的宽度较小且双棱镜的棱脊和光源狭缝平行，便可在白屏P 上观察到平行于狭缝的等间距干涉条纹如(图2)。

将白屏放到1P 、2P 区域中的任何位置，均可以看到明暗交替的干涉条纹。

设'd 代表两虚光源1S 和2S 间的距离，d 为虚光源所在的平面(近似的在光源狭缝S 的平面内)至观察屏P 的距离，若观察屏中央O 点与1S 、2S 的距离相等，则由1S 、2S 射束的两束光的光程差等于零，在O 点处两光波互相加强，形成中央明条纹；其余的明条纹分别排列在O 点的两旁。

假定Q 是观察屏上任意一点，它离中央点O 的距离为x 。

在'd d =时，121Δ'S S S 和ΔSOQ 可看做相似三角形，且有δ'xd d=(因QSO ∠很小，可用直角边d 代替斜边)，当 'δλx d k d ==(0,1,2,3k =±±±…）或 λ'dx k d ==(0,1,2,3k =±±±…）则两光束在Q 点相互加强，形成明条纹。

大学物理光的干涉详解

大学物理光的干涉详解

•
E1
完全一样（传播方向，频率， 相位，振动方向）
6
2. 光的单色性
例:普通单色光
: 10-2 10 0 Å 激光 ：10-8 10-5 Å 可见光 103Å
7
3. 光的相干性
相干光：满足相干条件的几束光
相干条件：振动方向相同，频率相同,有恒定的相位差
相干光相遇时合成光的振动：
nd
k 0,1, 2L
19
注意：① k 等于几，代表第几级明纹。 ② 零级明纹(中央明纹)由光程差=0决定。
暗纹 (2k 1) , k 1，2, 3L
2
k级暗纹位置: x (2k 1) D
nd
k 1，2, 3
注意：k=1第一级暗纹, k=2第二级暗纹…. 无零级暗纹
Imin
-4 -2 0 2 4
-4 -2 0 2 4
衬比度差 (V < 1)
衬比度好 (V = 1)
▲ 决定衬比度的因素：
振幅比，光源的单色性，光源的宽度
干涉条纹可反映光的全部信息（强度，相位）。 15
8. 半波损失：
当光从光疏媒质（折射率较小）入射到光密媒质（折 射率较大）再反射回光疏媒质时，在反射点，反射光损失 半个波长。 （作光程差计算时，在原有光程差的基础上加或减半波长）
干涉结果
明纹： 2k k
2
k 0,1, 2
36
① n1 n n2 ， n1 n n2
2e
n2

n12
sin2
i


2

k
k 1, 2, 3
注意：此处k等于几，代表第几级明纹，这

物理光学-第三章 光的干涉3.19

物理光学-第三章 光的干涉3.19
行等距直条纹。
5、干涉条纹的反衬度： 当两束光波满足获得稳定干涉的条件时有：
2 E 1 E 2 E 1 0 E 2 0 c o s k 2 k 1 r 2 0 1 0
干涉场强度为：
I r I 1 r I 2 r 2 I 1 I 2 c o s k 2 k 1 r 2 0 1 0
在三维干涉场中放置一个二维
y
的观察屏Π，Π上将出现强度
变化的干涉图形，这实际上是
极值强度面与观察平面的交线，
r
因此所谓的干涉图形又称为干
涉条纹。
O
z
P(r) Δk P0 Π
x
等强度面是按余弦规律变化的平行等距平面，Π平面上的干涉
条纹是一组平行等距的直线性条纹，条纹的方向及空间频率与
观察屏Π的方向有关
令Δ=L2-L1 ，称为P点对S1和S2的光程差
P点相对于光源点S1和S2的位相差： k 0 L 1 L 2 2 01 0
注意：
I1(P)和I2(P)分别是S1和S2单独在P点产生的强度 由于初始位相差是常量， 两光波在P点的位相位差取决于Δ
3、干涉场的分析 (1)、等强度面与等光程差面
y f
Π1垂直于f，该平面上|f1|=0，
Π4
Π2
Π1
干涉条纹为无限宽条纹
Π2平行于f，有|f2|=2 sin(θ/2)/λ，
α x
干涉条纹为平行等距直条纹；
Π3 二维观察屏的干涉条纹
Π3平行于x轴，该平面|f3|=2sin(θ/2)cosα/λ，干涉条纹为平行等 距直条纹；
Π4平行于y轴，该平面|f4|=2 sin(θ/2)sinα/ λ，干涉条纹也是平
将干涉强度的极大值和干涉强度的极小值代入，得到两束平 面波干涉的条纹反衬度公式：

第十一章波动光学(1)—光程差分波面干涉

第十一章波动光学(1)—光程差分波面干涉

长波无线电波
红外线 760nm 短波无线电波
紫外线 400nm X射线
可见光

射线
波长 m 10 8
10 4
10 0
10 4
10 8
10 12
10 16
无线电波 3 10 4 m ~ 0 . 1cm 5 红外线 6 10 nm ~ 760nm 可见光 760 nm ~ 400 nm
求 此云母片的厚度是多少？
解 设云母片厚度为d。无云母片时，零级亮纹在屏上P点，
到达P点的两束光的光程差为零。加上云母片后，到达P 点的两光束的光程差为
(n 1)d
当 P 点为第七级明纹位置时
7
d 7 n 1 7 550 10 1.58 1
6
P
d
6.6 10 mm
第十一章 波动光学
11-1 11-2 光的相干性 光程 分波面干涉
11-3
分振幅干涉
11-4 光的衍射 4-0 第四章教学基本要求 11-5 衍射光栅 4-0 第四章教学基本要求 11-6 光的偏振 4-0 第四章教学基本要求
* 光学发展简史
十七世纪以前 几何光学

十七世纪后半叶
微粒说(牛顿) 机械波动说(惠更斯)
假定 1 0
2 0，则：

2 r2
n2
2

2 r1
s1
*
r1
n1
n1
P
s 2*
r2
n2


( n 2 r2 n 1 r1 )

2 r2
n2

2 r1
n1

2

光的干涉(复习课讲稿)

光的干涉(复习课讲稿)

例、在双缝干涉实验中，在屏幕上P点处是明条纹， 若将缝S2遮盖住，并在S1、S2连线的垂直平分面处 放置一反射镜M，如图所示，则【 】 （A）P点处仍然是明纹； （B）P点处为暗纹； （C）不能确定P点处是明纹还是暗纹； （D）无干涉条纹。 S1 S S2 M
P
例、在杨氏双缝干涉实验中，两条缝的宽度原来是 相等的，若将其中一条缝的宽度略变窄，则【 】 （A）干涉条纹的间距变宽； （B）干涉条纹的间距变窄； （C）干涉条纹的间距不变，但原来极小处的强度不 再等于零； （D）不再发生干涉现象。 例、用白光进行双缝实验，若用纯红色的滤光片遮盖 一条缝，用纯蓝色的滤光片遮盖另一条缝，则【 】 （A）产生红色和蓝色两套干涉条纹； （B）条纹的宽度发生变化； （C）干涉条纹的亮度发生变化； （D）不产生干涉条纹。
课堂练习、波长为的平行单色光以角斜入射到缝间 距为d的双缝上，若双缝到屏的距离为D（D>>d）， 求： (1)条纹与正入射相比有何变化？（2）若欲使零 级明纹恢复到屏幕的O点处，应在哪个狭缝放置厚度 为多少的折射率为n的透明介质薄片。

S1 S2
P
O
第三讲 薄膜干涉
利用薄膜上、下两个表面对入射光的反射和 折射，可在反射方向(或透射方向)获得相干光束。 一、薄膜干涉 扩展光源照射下的薄膜干涉
1 2 n1>n2>n3 无附加光程差
n1<n2<n3 无附加光程差
n1 n2 n1>n2<n3 附加光程差/2 n1<n2>n3 附加光程差/2
n3
例、在真空中波长为的单色光，在折射率为n的透明 介质中从A沿某路径传播到B，若A、B两点的相位差 为3，则此路径AB的光程为：【 】 （Ａ）1.5 ； （B）3 ； （C）1.5 /n；（D）3 /n

11-2杨氏双缝干涉实验 劳埃德镜

11-2杨氏双缝干涉实验 劳埃德镜
’
第 十一章 光学9Fra bibliotek4.* 强度及强度分布
I1 ≈ I 2 = I 0 (Q r1 ~ r2 )
S1
S
r1
θ
p
r2
d
S2
θ
x o
δ ≈ d sin θ
I p = I1 + I2 + 2 I1I2 cos ∆ϕ
0 0 0
d’ d << d '
∆φ = 2I + 2 I cos ∆φ = 4 I cos 2
第 十一章 光学
14
物理学
第五版
1111-2 杨氏双缝干涉实验 劳埃德镜
已知 d = 0.2 mm d ’ = 1 m 求 (1) ∆x14 = 7.5 mm λ = ? ) (2) λ = 600 nm ∆ x ’ = ? ) d’ 解 (1) xk = ± kλ , k = 0 , 1, 2,L ) d ’ d ∆x14 = x4 − x1 = (k 4 − k1 )λ d d ∆x14 λ= = 500 nm d ' (k 4 − k1 ) ’ 1d ’ λ = 1.5 mm (2) ∆x = ) 2d
洛埃镜的光程差
N
第 十一章 光学
18
物理学
第五版
1111-2 杨氏双缝干涉实验 劳埃德镜
例2 如图 离湖面 h = 0.5 m处有一电磁波接 收器位于 C ，当一射电星从地平面渐渐升 起时， 起时， 接收器断续地检测到一系列极大 值 . 已知射电星所发射的电磁波的波长为 求第一次测到极大值时， 20.0 cm,求第一次测到极大值时，射电星 的方位与湖面所成角度. 2
∆x ∝ λ
白光入射时， 级明纹中心为白色 白光入射时，0级明纹中心为白色 可用来定0级位置 级位置） （可用来定 级位置）

双棱镜干涉

双棱镜干涉

双棱镜干涉实验目的(1) 观察双棱镜干涉现象,测量钠光的波长。

(2) 学习和巩固光路的同轴调整。

实验方法原理双棱镜干涉实验与双缝实验、双面镜实验等一样，都为光的波动学说的建立起过决定性作用，同时也是测量光波 波长的一种简单的实验方法。

双棱镜干涉是光的分波阵面干涉现象，由 S 发出的单色光经双棱镜折射后分成两列，相当 于从两个虚光源 S 1和 S 2射出的两束相干光。

这两束光在重叠区域内产生干涉，在该区域内放置的测微目镜中可以观察 到干涉条纹。

根据光的干涉理论能够得出相邻两明（暗）条纹间的距离为 ∆x = d Dλ ，即可有λ =d ∆x 其中 d 为两 D个虚光源的距离，用共轭法来测，即 d = ；离距的镜目微实验步骤(1) 仪器调节 ① 粗调d 1d 2；D 为虚光源到接收屏之间的距离，在该实验中我们测的是狭缝到测 。

量测镜目微∆测 x 由，小很将缝的位置放好，调至坚直，根据缝的位置来调节其他元件的左右和高低位置，使各元件中心大致等高。

② 细调根据透镜成像规律用共轭法进行调节。

使得狭缝到测微目镜的距离大于透镜的四倍焦距，这样通过移动透镜能够在 测微目镜处找到两次成像。

首先将双棱镜拿掉，此时狭缝为物，将放大像缩小像中心调至等高，然后使测微目镜能够接收到两次成像，最后放入双棱镜，调双棱镜的左右位置，使得两虚光源成像亮度相同，则细调完成。

各元件中心基本达到同轴。

(2) 观察调节干涉条纹调出清晰的干涉条纹。

视场不可太亮，缝不可太宽，同时双棱镜棱脊与狭缝应严格平行。

取下透镜，为方便调节可先将测微目镜移至近处，待调出清晰的干涉条纹后再将测微目镜移到满足大于透镜四倍焦距的位置。

(3) 随着 D 的增加观察干涉条纹的变化规律。

(4) 测量① 测量条纹间距 ∆x② 用共轭法测量两虚光源 S 1和 S 2的距离 d③测量狭缝到测微目镜叉丝的距离 D 数据处理测∆x数据记录条纹位置次数起始位置 a 终了位置a′被测条纹数mm|a-a′|∆x1 2 3 4 5 6 8.0953.5548.0303.5508.1843.5933.5758.0353.5738.1003.6808.0801010101010104.5204.4814.4574.5504.5044.4870.45200.44810.44570.45500.45040.4487x= 0.44998mm测 d 数据记录mm次数放大像间距 d1a1a1′缩小像间距d2|a1-a1′|a2a2′|a2-a2′|1 2 3 4 5 6 7.5605.7717.5385.7557.5205.7355.7747.5615.7667.5495.7537.5151.7861.7901.7721.7941.7671.7807.3576.9337.3816.9107.3556.9516.9657.3606.9687.3306.9407.3600.4100.4280.4130.4200.4150.409d1= 1.7915mm；d2= 0.4158mm测 D 数据记录mm狭缝位置 b1(1) ∆x的不确定度测微目镜差丝位置b′660∆D=|b-b′|659u A( ) = 0.001329mm；( ) 2 2 u B( ) = 仪3 = 0.005770mm；u u A( x) + u x0.005921mm。

13分波面双光束干涉(精)

13分波面双光束干涉(精)
4
所以，普通光源的光波特点： 1º 原子振动时随机的发出“有限长的波列” 2º 各波列之间没有恒定的位相关系，即：每个波列的初位相 各不相同。 3º 自然光:E矢量振动方向包含与传播方向垂直的一切可能的 振动方向。
两个独立的光源不可能成为一对相干光源
原因：原子发光是随机的，间歇性的，两列光波的振 动方向不可能一致，位相差不可能恒定。 两束光 不相干！
暗纹
d
光程差： r r2 r1 d sin 相位差：
程差条件

位置条件 暗纹
y (2 j 1)
r0 2d
(j 0,1,2)
13
条纹间距:
r0 y yk 1 yk d
y y P r1 ·y r2 0 r0

d
r

y0
y I
14
15
条纹分布区域在光线相遇的阴影区内。
28
3、洛埃镜
▲
实验装置
S1
① ①
M
P
y
P
②
d
S2
②
L
o
r0
最小
最大
最小
29
条纹特点 在光线相遇的阴影区内，干涉花样为与狭缝光源平 行、等间距、明暗相间条纹。 把屏幕 P 移到和镜面相接触的位置P ，s1 和s 2 到接 触点 L 的路程相等，似乎接触点应出现亮纹，实验事实 是接触点是暗纹。
8
(二)、几种典型的分波面干涉实验
1、杨氏实验 杨氏实验是分波面干涉最著名的例子，分析 杨氏实验，可了解分波面干涉的一些共同特点。 ▲ 实验装置 r1 单色光入射

d
r
P y r2
0

·y

分波阵面干涉

分波阵面干涉
a
•得
ax 0.45103 1.2103
D
540 109
1.0m
1.1 杨氏双缝干涉实验
•
(2)
在S2
未被玻璃片遮盖时，光程差为
r2
r1
a D
x
中央亮条纹的中心应处于 x=0的地方。遮盖厚度为 h的玻璃片
后，透射光中没有半波损失，但是中央亮条纹的光程差变为
(r2
h
nh)
r1
h(n 1)
r2
r1
1.1 杨氏双缝干涉实验
• 例题3-2 在杨氏双缝干涉实验中，双缝间距为0.45mm， 用波长为540nm的单色光照射。
• (1) 要使光屏E上条纹间距为1.2mm，光屏应离双缝多远?
• (2) 若用折射率为1.5、厚度为9.0m的薄玻璃片遮盖狭缝 S2 ，光屏上干涉条纹将发生什么变化?
• 解: (1) 根据干涉条纹间距的表达式 x D
•
a ＝Dλ／Δx ＝1.65 ×10-4 m
1.2 半波损失
• 劳埃德镜平面镜的干涉，相当于光源S1和它在平面镜中的虚 像S2发出的两束光的干涉，与杨氏双缝干涉类似。
• 劳埃德将屏E移到与平面镜接触的N位，发现N处的屏上出 现的是暗条纹。而此处到S1和S2光程相等，似乎应该出现 亮条纹，为什么观察到的却是暗条纹呢？
大学物理
分波阵面干涉
• 1.1 杨氏双缝干涉实验 • 1.2 半波损失
1.1 杨氏双缝干涉实验
• 如果两列光波到达屏上P点的光程差 等于波长的整数倍， 两列光波到达P点时的位相相同，叠加后互相加强，P点 就出现亮条纹；
• 如果光程差 等于半波长 的 奇数倍， 两列光波到达 P点时的位相 相反，叠加后 互相减弱或抵消， 就出现暗条纹。

平行平板产生的干涉.

平行平板产生的干涉.

MgF2, n=1.38),用以增加透射，这个薄膜,就是增透膜。
反射相干光满足相消干涉 条件来减少反射：
2n2 h (2m 1)

膜
n1=1.0 n2=1.38 n3=1.50
2 (m 0, 1, 2)
hmin

4n2
n2h——光学厚度
增反膜----利用薄膜上、下表面反射光的光程差满足相长干涉 ，因此反射光因干涉而加强。 与增透膜相反,在另一些光学系统中希望光学表面具有很高 的反射率(如He–Ne激光器要求反射99%)，这时可在元件表 面多层镀膜以增强反射,这类薄膜称为增反膜或高反射膜。
透射光的干涉：
对于同一入射角的光束来说，
i
A 2
C
n1 n2 n1
D
B
e
两支透射光的光程差和两支反 射光的光程差恰好相差半个波 长，当对应某一入射角的透射 光条纹是亮纹时，反射光条纹 是暗纹。透射光的等倾条纹和 反射光的等倾条纹是互补的。
对于同一厚度的薄膜，在某一方向观察到某一波 长对应反射光相干相长，则该波长在对应方向的
D 2h n2 2 n12sin 21 2hn2
h 1.25 1.50
无反射意味着反射光出现暗纹，所以
1 D 2hn2 (m ) 2
(m=0,1,2,……)
n2=1.25(薄膜的折射率);要h最小，m =0
h

4n2
=1.2×10-7m
例题 阳光垂直照射在空气中的肥皂膜上，膜厚h=380nm, 折射率n2=1.33 ，问：肥皂膜的正面和背面各呈什么颜色？ 解 正面反射加强，有
薄膜技术的应用
在薄膜干涉中，光线一部分被反射，另一部分则透射进入介质。 反射光干涉极大时，光线大部分被反射。反射光干涉极小时， 光线大部分被透射。通过控制薄膜的厚度，可以选择使透射或

平行平板产生的干涉

平行平板产生的干涉

MgF2, n=1.38),用以增加透射，这个薄膜,就是增透膜。
反射相干光满足相消干涉 条件来减少反射：
2n 2e ( 2k 1) 2 (k 0, 1, 2)
n1=1.0
膜
n2=1.38 n3=1.50
λ emin = 4n 2
n2e ——光学厚度
2nh cos 2 2
n1 1
n2 1.38
d
2n2 d (2k 1) / 2
n3 1.5
代入k 和 n2 求得：
3 3 550 10 9 d 2.982 10 7 m 4n2 4 1.38
n1 1
n2 1.38
此膜对反射光相干相长的条件：
d
2n2 d k
代入d和n2 求得：

L d L
2 2 2

2
S
d
L
P
d L ( 1 2 1) L 2 d2 2 (1 2L 2
s
1 2
C
1 x) 1 x ..... 2
d 2 1 33 2 L
2
S
d
L
P
满足
(2k 1) / 2
s
C
故，P点为暗条纹
(3)由反射相消干涉条件为：
2n2e 2k＋1 , 2

k 0,1,2,
2k 1 e
4n2
显然k=0所产生对应的厚度最小，即
emin 550 113nm 4n2 4 1.22

例
波长为 的点光源S与屏的距离为L，一反射镜C与屏垂直放
置，直接来自光源的光线SP与镜面平行，且与从镜面反射的光线 相遇相干。设 5 107 m ，L=1m，d=4×10-3m，试讨论P点干涉结 果？屏幕上相邻明条纹的间距为多少？ [解]： S‘为虚光源，相干光视为由S 、S’ 分别发出。

2011 物理光学2-1(3)分振幅干涉

2011 物理光学2-1(3)分振幅干涉
问：若反射光干涉相消的条件中 取 j=１，膜的厚度为多少？此增 透膜在可见光范围内有没有增反？
n1 1
n2 1.38
解：因为 n1 n2 n3 ，所以反 射光经历两次半波损失。反射光干 涉相消的条件是：
h
2 3 3 550 109 代入j 和 n2 求得： h 2.982 107 m 4n2 4 1.38
j
等倾亮圆环的半径
1 rN f n0 n N 1 h
f为透镜焦距
较厚的平行平板产生的等倾干涉圆环，其半径要 比较薄的平板产生的圆环半径小。 由
rN
中 心 等倾圆环相邻条纹的间距 向 f n 外 eN rN 1 rN 2n0 h( N 1 ) 计 算 ， 第 愈向边缘(N愈大)，条纹愈密；反之，亦然。

2
图 2-11 楔形平板的干涉
对于一定的入射角光程差只依赖于反射光处的平板厚度 h， 所以，干涉条纹与楔形板的厚度一一对应。因此，这种干涉称 为等厚干涉，相应的干涉条纹称为等厚干涉条纹。
图 2-12 观察等厚干涉的系统
2.等厚干涉条纹图样 不同形状的楔形板将得到不同形状的干涉条纹。图(a)楔 形平板、(b) 柱形表面平板、(c)球形表面平板、(d)任意 形状表面平板的等厚干涉条纹。不管哪种形状的等厚干涉 条纹，相邻两亮条纹或两暗条纹间对应的光程差均相差一 个波长，所以从一个条纹过渡到另一个条纹，平板的厚度 均改变λ /（2n)。
(2) 楔形平板产生的干涉——等厚干涉
1.光程差的计算公式
扩展光源中的某点S0发出一束光 ，经楔形板两表面反射的两束光 相交于P点，产生干涉，其光程 差为
楔形平板产生干涉的原理
Δ=n(AB+BC)-n0(AP-CP)

《大学物理(上)》光的干涉

《大学物理(上)》光的干涉
★ 结论：薄透镜不会引起各相干光之间的附加光程差。
20
万物之美 科学之理
目录
第一节 光源 光波 光的相干性 第二节 光波的叠加 光程与光程差 第三节 分波阵面干涉 第四节 分振幅干涉 第五节 迈克尔逊干涉仪 第六节 迈克尔逊干涉仪
第三节 分波阵面干涉
杨氏双缝干涉实验
实验现象
s1
S
s2
明条纹位置 明条纹位置 明条纹位置
42
第四节 分振幅干涉
43
第四节 分振幅干涉
练一练 观察 n=1.33 的薄油膜的反射光，它呈波长为 500nm 的绿光， 且这时法线和视线夹角 i=45o
求 （1）膜的最小厚度
i
（2）若垂直观察，此膜呈何种颜色
d
解 （1） 绿光干涉相长
数据代入（k=1）： （2） 垂直观察
深黄色
44
第四节 分振幅干涉
P
S1
r2 d
x
2
1
0
I
S2
D
1
x
2
25
第三节 分波阵面干涉
讨论
D、d 一定时， x 或 x
若用白光照射双缝，屏上中心明纹仍为白色，两侧对称分布各级紫内红 外的彩色条纹。更高级次的彩色条纹可能会发生重叠 。
0
1
2
3
0 1 23 4
中央明纹
3
2
1
0
1
2
3
26
第三节 分波阵面干涉 洛埃镜
M
S1 •
5
第一节 光源 光波 光的相干性
光波
1、颜色与光波
光色 波长(nm)
可
红
760~622
见
光 七

分波阵面干涉

分波阵面干涉
出，放置介质片之后，零级亮纹下移。
典型例题
(2)在没有放置介质片时， S1
原来的-k级亮纹的位置
满足:
S2 d
r1 光轴
r2
r2 r1 k 0 k 0 ,1,2 ,
按题意，可得介质片厚度 d k0
n1
主要内容
1、其他分波阵面的干涉 2、薄膜等倾干涉 3、等倾干涉例题
劈尖干涉，牛顿环，迈克尔逊干涉仪
典型例题
[例2] 在杨氏双缝干涉的实验装置中，入射光的波长
为λ。若在缝S2与屏之间放置一片厚度为d、折射率 为n的透明介质片，试问：
(1) 原来的零级亮纹 将如何移动？
(2) 如果观测到零级 亮纹移到了原来
的-k级亮纹处，
求该透明介质的
厚度d。
S1 S2
d
r1 光轴 r2
二、光程
问题
光在介质中和在真空中传播相同 距离用时是否相同？
L = L2 - L1
典型例题
[例2] 在杨氏双缝干涉的实验装置中，入射光的波
长为λ。若在缝S2与屏之间放置一片厚度为d、折射 率为n的透明介质片，试问：
(1) 原来的零级亮纹 将如何移动？
(2) 如果观测到零 级亮纹移到了原
来的-k级亮纹处，
求该透明介质的
厚度d。
S1 S2
d
r1 光轴
r2
典型例题
解：用几何光学方法不难
求出，S 经上、下两个 半个透镜L1、L2分别成 像于S1与S2。
它们位于透镜右侧 40cm 处(实像)，可 看成新的光源， 与屏之间的距离
S1
40cm S2
80cm
D 160 40 40 80cm
S1与S2组成相干光源，其光线在屏幕上重叠（阴影区）处 产生干涉条纹，即可求出干涉条纹的间距

7.2 分波面法干涉

7.2 分波面法干涉

二、菲涅耳双面镜
S
光栏
W
M1
虚光源 S 1 S 、 2
S 1 S 2 平行于 WW '
d
S1
x
C
o
M2
S2
W'
d D
D
屏幕上O 点在两个虚光源连线的垂直平分线上，屏幕 上明暗条纹中心对O点的偏离 x为：
x k D d
明条纹中心的位置

D d
k 0 , 1, 2
x
2k 1 2
明纹、暗纹位置
kD a ( k 0 ,1,2 ) 明纹
x
( 2k 1)
D
2a
( k 0 ,1, 2 ) 暗纹
Guangxi university
干涉条纹图样
632.8nm的氦氖激光器产生的干涉条纹
589.3nm的钠黄光产生的干涉条纹
Guangxi university
讨论
明 纹
1.明纹位置
a k=0时： x 0 0 xk kD
O
0
I
零级明纹位 于屏幕中央，只 有一条。
Guangxi university
k=1时：
x1
明 纹
D
a
O
4
3 2 1
1 2 3 4
1级明纹有两条， 对称分布在屏幕中 央两侧。 其它各级明纹都 有两条，且对称分 布。
第二节
分波面法干涉
Guangxi university
返回
一、杨氏双缝干涉
杨氏双缝干涉实验 是最利用单一光源形 成两束相干光，从而 获得干涉现象的典型 实验。它是属于分波 阵面法干涉。
Guangxi university

大学物理-课件：17.2分波阵面法干涉

大学物理-课件：17.2分波阵面法干涉

d 2n 1 R
D RL
n,
R
L
x D
d
第二节
托马斯.杨
一、杨氏双缝干涉实验
1、实验装置及条纹形状
x
x S1
S S2
2、明暗纹条件及条纹间距
光强分布 I 2E02 r2
P x O
S2 r2 r1
D ( d )
在两个相似三角形中

x
x


d D2 x2 D
d x
D
2、明暗纹条件及条纹间距
光强分布 I 2E02 1 cos 2π
x
S1
r1
P
x
x

r2
Sd
S2 r2 r1
dx O
x
D
D ( d )
明纹


k
，
x明

k
D
d
，
k 0,1, 2
暗纹

2k 1
2
，x暗
2k 1 D
光的相位差为 ，相当于光程差
，称为 半波损失。
双棱镜实验
d 2n 1 R
D RL
n,
x D
R
d
x D
L
d
洛埃镜实验
x D
d
紧靠镜端处总是产生暗纹，说明在镜端处反射光与入射光
的相位差为 ，相当于光程差
，称为 半波损失。
双面镜实验
x D
d
双棱镜实验
x
S1
r1
P
x
x

r2
Sd S2 r2 r1

408-分波阵面干涉

408-分波阵面干涉

408分波阵面干涉1，一束波长为λ的光线，投射到一双缝上，在屏幕上形成明、暗相间的干涉条纹，那么对应于第一级暗纹的光程差为：(A)2λ(B)1/2λ(C)λ(D)λ/4[ ] 2，用单色光做双缝干涉实验，下述说法中正确的是（A）相邻干涉条纹之间的距离相等（B）中央明条纹最宽，两边明条纹宽度变窄（C）屏与缝之间的距离减小，则屏上条纹宽度变窄（D）在实验装置不变的情况下，红光的条纹间距小于蓝光的条纹间距[ ] 3，在杨氏双缝干涉实验中，正确的叙述是：(A) 增大双缝间距，干涉条纹间距也随之增大(B) 增大缝到观察屏之间的距离，干涉条纹间距增大(C) 频率较大的可见光产生的干涉条纹间距较大(D) 将整个实验装置放入水中，干涉条纹间距变大[ ] 4，用单色光垂直照射杨氏双缝时，下列说法正确的是：(A) 减小缝屏距离，干涉条纹间距不变(B) 减小双缝间距，干涉条纹间距变小(C) 减小入射光强度, 则条纹间距不变(D) 减小入射波长, 则条纹间距不变[ ] 5，在双缝干涉实验中，为使屏上的干涉条纹间距变大，可以采取的办法是：(A) 使屏靠近双缝(B) 把两个缝的宽度稍微调窄(C) 使两缝的间距变小(D) 改用波长较小的单色光源[ ] 6，双缝干涉实验中，入射光波长为λ，用玻璃纸遮住其中一缝，若玻璃纸中光程比相5.2，则屏上原0级明纹中心处同厚度的空气大λ（A）仍为明纹中心（B）变为暗纹中心（C）不是最明，也不是最暗（D）无法确定[ ] 7，用单色光做杨氏双缝实验，如现将折射率n=1.5的薄透明玻璃片盖在上侧缝上，此时中央明纹的位置将：(A ）向上平移且条纹间距不变 （B ）向下平移，且条纹间距不变 （C ）不移动，但条纹间距改变 （D ）向上平移，且间距改变[ ]8，在双缝干涉实验中，设缝是水平的，若双缝所在的平板稍微向上平移（如图），其他条件不变，则屏上的干涉条纹： （A ）向下平移，且条纹间距不变 （B ）向上平移，且条纹间距不变 （C ）不移动，但条纹间距改变 （D ）向上平移，且间距改变[ ]9，杨氏双缝干涉实验中，下列说法正确的是（k 为自然数，λ为光波波长） ①在距双缝的路程相等的点形成暗条纹 ②在距双缝的路程差为k λ的点形成亮条纹③在距双缝的路程差为k2λ的点形成亮条纹 ④在距双缝的路程差为(k+21)λ的点形成暗条纹（A ）①② （B ）②③ （C ）③④ （D ）②④[ ]10，如图所示，用波长600=λnm 的单色光做杨氏双缝实验，在光屏P 处产生第五级明纹极大，现将折射率n =1.5的薄透明玻璃片盖在其中一条缝上，此时P 处变成中央明纹极大的位置，则此玻璃片厚度为：（A ）5.0×10-4cm （B ）6.0×10-4cm （C ）7.0×10-4cm （D ）8.0×10-4cm[ ]11，在双缝干涉实验中，先后用红光和紫光在相同条件下照射同一双缝，则在屏上出现的干涉条纹中，这两种色光的两明条纹间的距离和两暗纹间距离相比较： (A) 红光都比紫光大 (B) 紫光都比红光大 (C) 红光两明纹间距离比紫光大，两暗纹间距离比紫光小 (D) 紫光两明纹间距离比红光大，两暗纹间距离比红光小[ ]SS12，在双缝干涉中，屏幕E上的P点处是明条纹，若将缝s2 Array盖住，并在s1 s2 连线的垂直平分面处放一反射镜M，如图所示，则此时：(A) P点处仍为明条纹(B) P点处为暗条纹(C) 不能确定P点处是明条纹还是暗条纹(D) 无干涉条纹[ ] 13，用单色光做杨氏双缝实验，如现将折射率n=1.5的薄透明玻璃片盖在下侧缝上，此时中央明纹的位置将：(A）向上平移且条纹间距不变（B）向下平移，且条纹间距不变（C）不移动，但条纹间距改变（D）向上平移，且间距改变[ ] 2. 判断题：1，在双缝干涉实验中，为使屏上的干涉条纹间距变大，可以采取的办法是使两缝的间距变小。

第十章 波的干涉

第十章 波的干涉

λ δ = r2 − r1 = ±(2k − 1) 2
第5页
k= 1, 2, 干涉减弱条件
其中δ为波程差
★从波程差δ=r1-r2角度考虑波的干涉：
±kλ δ = r2 − r1 =
k= 0,1, 2,
干涉加强条件
λ δ = r2 − r1 = ±(2k − 1) 2
k= 1, 2, 干涉减弱条件
光程差
波程差
δ
∆r = r2 − r 1
光程差 (两光程之差) 相位差
δ = L2 − L1 = n2 r2 − n1r1
r2 r1 t t ( ) +ϕ )20 − 2 = ∆ϕ 2π( π − − + ϕ10 T λ2 T λ1 2π2π = (ϕ 20 − ϕ10 ) − ( n2 r2 − n1r1 ) = (ϕ20 − ϕ10 ) −
x=
D ±k λ d λ D ± (2k − 1) d 2
k = 0,1,2,
明纹 暗纹
Dλ ∆x = d
k = 1, 2,
4.干涉条纹间距： 相邻两明（纹或暗纹）间的间距为：
第 15 页
3、讨论
（1）其两侧明暗条纹对称分布
x = 0 有 k = 0 —中央明条纹
（2）条纹间距
∆x 与 λ 、d 的关系
第2页
二、波的干涉(interference) 干涉现象:几列波在相遇的叠加区域内，某些点的振动始 终加强，而另有一些点的振动始终减弱。 相干条件： 1.波的振动频率相同， 2.振动方向相同， 3.振动相位相同或有恒 定的相位差。
S1
S2 能产生干涉现象的两列波叫做 相干波（coherent wave）
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

11.3.3 光的空间相干性和时间相干性
1．空间相干性 ． 具有一定宽度的面光源S 具有一定宽度的面光源 可以看成是由 无数条线光源组成的， 无数条线光源组成的，每一条线光源各自在 屏幕上形成自己的一套干涉条纹． 屏幕上形成自己的一套干涉条纹．由于各线 光源的位置不同， 光源的位置不同，它们在屏幕上的干涉条纹 之间有一定的相对位移．光源宽度越大， 之间有一定的相对位移．光源宽度越大，同 级条纹在空间的分布范围越大． 级条纹在空间的分布范围越大．当各套条纹 的最大位移等于或大于条纹间距时， 的最大位移等于或大于条纹间距时，干涉条 纹消失. 纹消失. 这种与扩展光源宽度有关的干涉性称为光 的空间相干性. 的空间相干性.
考虑第级明纹的位置． （2）考虑第级明纹的位置．由明纹条件 k = 0,1,2,L δ = r2 − r1 + ( n − 1)l = ± kλ 代入上式， 将 代入上式，可求得加媒质 片后第 k 级明纹的位置 x′为 D D ' xk = ± k λ − ( n − 1)l d d
D 未加媒质片时 xk = ± k λ d
相邻两明纹（或暗纹）中心间的距离: 相邻两明纹（或暗纹）中心间的距离: D ∆x = xk +1 − x k = λ d
11.3.2 洛埃镜实验
E′
E
光程差为
δ = r2 − r1 +
λ
2
s1 s2
k
L
因为从 s2 发出的光线都有半波损失,所以 发出的光线都有半波损失, 的附加光程差. 必须加 λ 2 的附加光程差. 平面反射镜与光屏 E ′ 的交线理论上应是 暗条纹,实验的确如此.所以说, 暗条纹,实验的确如此.所以说,洛埃镜实验验 证了半波损失理论. 证了半波损失理论.
两式相减得: 两式相减得
r22 − r12 = ( r2 − r1 )(r2 + r1 ) = 2dx
因为D >>d，所以当x <<D 因为 >> ，所以当 << 时,r1 + r2 ≈ 2 D
d δ = r2 − r1 = x D 设入射光波长为 λ
则:
± kλ 明纹中心） 干涉相长（明纹中心） λ δ = 暗纹中心） ± ( 2k + 1) 2 干涉相消（暗纹中心）
2．时间相干性 ． 因为光源总有一定的谱线宽度∆λ ，由于∆λ 范围内的每一个波长的光都会形成各自的一套 干涉条纹， 干涉条纹，且除零级以外各套条纹间都有一定 的位移， 的位移，所以它们非相干叠加的结果会使总的 干涉条纹的清晰度下降． 干涉条纹的清晰度下降．当 D D kc ( λ + ∆λ ) = ( kc + 1) λ d d λ 时,总的干涉条纹消失 kc = ∆λ
λ2 显然有： l0 = δ c = 显然有 ∆λ
可见，光源的单色性越好， 可见，光源的单色性越好，光源的谱线宽 就越小，波列的长度就越长． 度 ∆λ 就越小，波列的长度就越长．
在杨氏双缝装置中， 例1 在杨氏双缝装置中，若在下缝后放一 折射率为n，厚为L的透明媒质薄片 的透明媒质薄片， 折射率为 ，厚为 的透明媒质薄片，如图所 示． 求两相干光到达屏上任一点P的光程差 的光程差； （1）求两相干光到达屏上任一点 的光程差； 分析加媒质片前后干涉条纹的变化情况． （2）分析加媒质片前后干涉条纹的变化情况 （ ） 解： 1）加媒质 P r1 x 片后两光束到达P 片后两光束到达 s1 点的光程差 r2 d 0 δ = [(r2 − l ) + nl ] − r1 s2 L D = r2 − r1 + ( n − 1)l
k = 0,1,2,L
干涉条纹各级中心位置可表示为 D 明纹中心 ±k λ d x= D λ ± ( 2k + 1) ⋅ 暗纹中心 d 2
k = 0,1,2,L
k 为干涉条纹的级次，正负号表示各级干 为干涉条纹的级次， 涉条纹对称分布在中央明纹（ 的两侧． 涉条纹对称分布在中央明纹（ k = 0）的两侧．
λ 实现相干的最大光程差 δ c = kc (λ + ∆λ ) ≈ ∆λ
2
相干光必须来自同一个原子同一次发射 的波列，而这种波列的长度（光程） 的波列，而这种波列的长度（光程）为 l0 = cτ 0 τ 0 为波列持续的时间, l0 是两相干波的最大 为波列持续的时间, 光程差．显然，波列的长度越长， 光程差．显然，波列的长度越长，则这两个 波列在相遇点相互叠加的时间就越长， 波列在相遇点相互叠加的时间就越长，干涉 现象越明显． 现象越明显．这个性质称为时间相干性
D ∆xk = x − xk = − ( n − 1) l d
' k
d r2 − r1 = x Dቤተ መጻሕፍቲ ባይዱ
11.3 分波阵面干涉
11.3.1 杨氏双缝干涉 11.3.2 洛埃镜实验 11.3.3 光的空间相干性和时间相干性
11.3.1 杨氏双缝干涉
P
r1
s
s1 d s2
r2
x
O
D
光程差为 δ = r2 − r1 由几何关系有 d 2 d 2 2 2 2 2 r2 = D + ( x + ) r1 = D + ( x − ) 2 2