下载文档原格式
平面杆件体系的几何组成分析平面杆件体系是一种复杂的结构，它由许多杆件组成，而每一种杆件的几何组成都是关键因素，如果要正确地分析平面杆件体系的结构及其性能，就必须对其几何组成进行分析。
二、杆件的几何组成1.杆件的长度所有杆件的长度都受到几何限制，它们必须符合系统的几何特征。
对于构件来说，长度是其基本组成特征，它是决定构件在结构中执行何种功能的重要因素。
因此，在分析平面杆件体系的几何组成时，必须准确测量杆件的长度，并计算它们的变化范围等。
2.杆件的相对位置杆件的相对位置也是重要的几何特征，它决定了杆件之间的关系，也影响了杆件的功能表现。
一般来说，当分析杆件间的几何组成时，必须正确测量杆件间的间距及其尺寸比例，以确定杆件间的相对位置。
3.杆件的角度角度是杆件或构件之间的重要几何参数，它影响着构件间的连接及它们的力学性能。
因此，在研究平面杆件体系的几何组成时，也必须对不同杆件的角度进行测量，并进一步计算出各杆件之间的角度关系。
三、杆件的几何组成分析1.力学分析力学分析是研究杆件几何组成的重要方法，它可以从多个维度来研究构件的性能，并从力学角度来分析平面杆件体系的组成及其性能。
例如，可以通过力密度法对平面杆件体系的几何组成进行分析，以确定某一构件在结构中所承受的载荷情况，以及各构件之间的荷载传递情况。
2.静力学分析静力学是研究杆件几何组成的另一种重要方法。
它可以通过计算构件的力学参数，如构件的弹性模量、强度及抗剪模量等，从而确定平面构件体系的几何组成情况以及它们的力学特性。
3.拓扑分析拓扑分析是研究杆件几何组成的一种特殊方法，它旨在通过测量某一构件的几何组成参数，如构件的节点数、轴线关系、长度比例等，来确定平面杆件体系的几何组成，以及它们在结构中的作用及其性能。
四、总结平面杆件体系是一种复杂的结构，它由许多杆件组成，而杆件的几何组成则是研究平面杆件体系结构及性能的重要因素。
本文从三个方面介绍了杆件几何组成分析的方法：即力学分析、静力学分析和拓扑分析。
平面六杆机构的运动分析
1.确定机构的几何特性：首先，需要根据机构的构件和铰链的几何特
性确定机构的几何特性。
这包括确定构件的长度、铰链的位置和角度。
2.建立机构的运动方程：根据机构的几何特性，可以建立机构的运动
方程。
运动方程描述了机构各构件之间的运动关系，可以通过几何关系和
运动链法建立运动方程。
3.解决运动方程：通过求解运动方程，可以得到机构各构件的位置、
速度和加速度。
这可以通过数值方法或解析方法来完成。
4.分析机构的运动特性：根据机构的运动方程和解决的结果，可以分
析机构的运动特性。
这包括机构的平稳性、运动范围、速度和加速度的变
化等。
5.优化机构的设计：根据分析的结果，可以对机构的设计进行优化。
例如，可以调整构件的长度、角度和铰链的位置，以改善机构的运动性能。
总之，平面六杆机构的运动分析是研究和设计机械系统的重要步骤。
通过分析机构的运动特性，可以优化机构的设计，提高机械系统的性能和
效率。
因此，对平面六杆机构的运动分析有着重要的理论和实际意义。
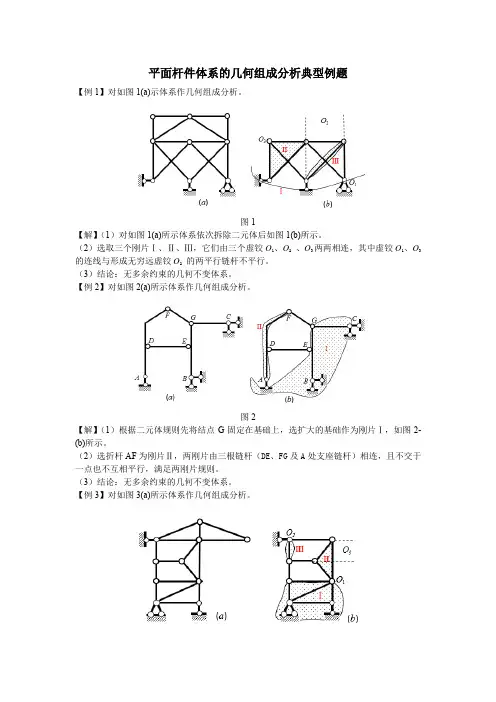
平面杆件体系的几何组成分析典型例题【例1】对如图1(a)示体系作几何组成分析。
图1【解】（1）对如图1(a)所示体系依次拆除二元体后如图1(b)所示。
（2）选取三个刚片Ⅰ、Ⅱ、Ⅲ，它们由三个虚铰O1、O2、O3两两相连，其中虚铰O1、O3的连线与形成无穷远虚铰O2的两平行链杆不平行。
（3）结论：无多余约束的几何不变体系。
【例2】对如图2(a)所示体系作几何组成分析。
图2【解】（1）根据二元体规则先将结点G固定在基础上，选扩大的基础作为刚片Ⅰ，如图2-(b)所示。
（2）选折杆AF为刚片Ⅱ，两刚片由三根链杆（DE、FG及A处支座链杆）相连，且不交于一点也不互相平行，满足两刚片规则。
（3）结论：无多余约束的几何不变体系。
【例3】对如图3(a)所示体系作几何组成分析。
图3【解】（1）对如图3(a)所示体系依次拆除二元体后如图3(b)所示。
（2）选取三个刚片Ⅰ、Ⅱ、Ⅲ，它们由三个铰O1、O2、O3两两相连，其中铰O1、O2的连线与形成无穷远虚铰O3的两平行链杆不平行。
（3）结论：无多余约束的几何不变体系。
【例4】对如图4所示体系作几何组成分析。
图4【解】对如图4(a)体系进行几何组成分析如下：（1）选取如图4(a)所示的两个刚片Ⅰ、Ⅱ，它们由三根链杆AC、EF及BD相连，且这三根链杆不交于一点也不互相平行，满足两刚片规则，因此上部体系是没有多余约束的几何不变部分。
（2）上部体系与基础间由四根支座链杆相连接。
（3）结论：有一个多余约束的几何不变体系（四根支座链杆中任一根均可看作多余约束）。
对如图4(b)体系进行几何组成分析如下：（1）先根据两刚片规则将杆123及结点7固定在基础上，再根据二元体规则依次固定结点4、5，扩大的基础刚片即刚片Ⅰ。
（2）固定结点6时，由于结点5、6、7共线，结论：几何瞬变体系。
【例5】对如图5(a)所示体系作几何组成分析。
图5【解】选取三个刚片Ⅰ、Ⅱ、Ⅲ，如图5(b)所示，它们由三个铰O1、O2、O3两两相连，其中铰O1、O2的连线与形成无穷远虚铰O3的两平行杆不平行。
07、基本知识趣谈平面体系的几何组成分析同学们学习下面内容后，一定要向老师回信（****************），说出你对本资料的看法（收获、不懂的地方、资料有错的地方），以便考核你的平时成绩和改进我的工作。
回信请注明班级和学号的后面三位数。
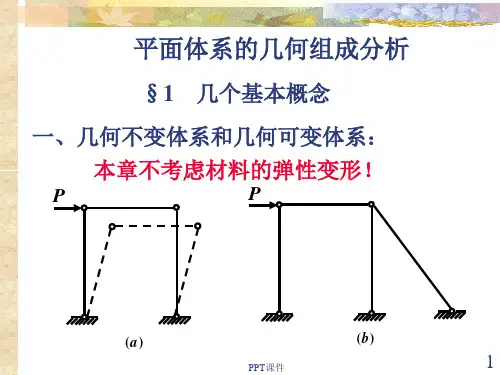
§1.问题的提出在人们眼中，每个建筑物天天都一个样，即建筑物是1能够承受一切工作荷载的、2静止在地面上的、3似乎没有任何变形的4人造物。
在土木工程中，建筑物的骨架称为“结构”，结构常常用所谓的“结构计算简图”来表述。
因此，“结构计算简图”必须首先体现人们眼中建筑物的3个“特征”。
如何在设计建筑结构计算简图时，不用计算分析，就能够判断出该图能否作为“结构的计算简图”呢？在没有判断前，这样的图只能够称之为“体系”，因为画出的体系可能不是结构的计算简图。
显然，作为建筑物骨架的“结构计算简图”，首先应该是人们眼中的建筑物雏形，即“1能够承受一切工作荷载的、2静止在地面上的、3似乎没有任何变形的”“体系”。
如果画出的体系不是这样的体系，就没有必要做进一步的设计分析计算等。
所以，在计算分析之前，判断画出的体系图是否可以作为“结构的计算简图”，是一个必不可少的重要环节之一。
这一工作，就是本章要专门研究的问题：如何判断一个画出的平面体系图，是否是人们眼中的建筑物骨架？这个工作可称为平面杆件体系的几何组成分析。
§2.几何不变体系和几何可变体系的定义1、体系物体的集合，称为体系。
2、刚体与刚片在任意荷载作用下，不计各个组成的三维物体本身变形的体系，称为刚体。
显然，该定义有2个要点：荷载任意和不计本身变形。
在任意荷载作用下，不计各个组成的、位于同一个平面的平面物体本身变形的体系，称为刚片。
显然，该定义有2个要点：荷载任意和不计本身变形。
由于只研究平面杆件体系，故后面只用刚片一词。
3、几何不变体系与几何可变体系在任意荷载作用下，不计各个组成的物体本身变形，而保持其几何形状大小和位置都不变的体系，称为“几何不变体系”。
第2章平面杆件体系的几何组成分析（知识点小结）一、几何组成分析的几个概念1、几何不变体系与几何可变体系几何不变体系是指受到任意荷载作用下，若不考虑材料的应变，其几何形状和位置均能保持不变的体系。
几何可变体系是指即使不考虑材料的应变，在微小的荷载作用下也会产生刚体位移，而不能保持原有的几何形状和位置。
几何可变体系分为几何常变体系和几何瞬变体系。
几何可变体系在很小的荷载作用下会产生位移，经微小位移后仍能继续发生刚体运动，这样的几何可变体系称为几何常变体系。
若原为几何可变体系，经微小位移后即转化为几何不变体系，这类几何可变体系为几何瞬变体系。
工程结构绝不能采用几何瞬变体系，而且也应避免采用接近于瞬变的体系。
2、自由度指体系在所受限制的许可条件下独立的运动方式，即能确定体系几何位置的彼此独立的几何坐标数目。
平面内一点的自由度为2，一个刚片的自由度为3。
3、约束（联系）约束是指指限制体系运动的各种装置。
约束包括外部约束（支座约束）和内部约束。
（1）外部约束一个活动铰支座、固定铰支座和固定支座分别相当于1、2、3个约束。
（2）内部约束一根单链杆相当于1个约束；连接m(m>2)个结点的复链杆，相当于2m-3个单链杆，即相当于2m-3个约束；一个单铰相当于2个约束；连接m(m>2)个刚片的复铰，可折合成(m-1)个单铰，即相当于2(m-1)个约束作用；一单刚结点相当于三个约束；联结m(m>2)个刚片的刚结点称为复刚结点，可折合成(m-1)个单刚结点，即相当于3(m-1)个约束。
约束从能否减少体系的自由度方面来划分，可分为必要约束和多余约束。
为保持体系几何不变所必须具有的约束称为必要约束,不能使体系的自由度数目减少的约束称为多余约束。
4、瞬铰(虚铰)两个刚片间用两个不共线链杆相联，其约束作用相当于这两根链杆交点位置处的一个铰所起的约束作用，这个铰称为虚铰或瞬铰（图2-1a）。
在几何组成分析中，尤其要注意这样特殊情况：两刚片间用两根相互平行的链杆相连，两根平行链杆所起的约束作用相当于无穷远处的瞬铰所起的约束作用，如图2-1b所示。
