常用连续型分布性质汇总及其关系
- 格式:doc
- 大小:422.12 KB
- 文档页数:7


常用连续型分布性质汇总及其关系1. 常用分布1.1 正态分布(1)若X 的密度函数和分布函数分别为()()()222222(),.,.x t xp x x F x e dt x μσμσ-----∞=-∞<<+∞=-∞<<+∞ 则称X 服从正态分布,记作()2~,,X N μσ,其中参数,0.μσ-∞<<+∞>(2)背景:一个变量若是由大量微小的、独立的随机因素的叠加结果,则此变量一定是正态变量。
测量误差就是由量具零点偏差、测量环境的影响、测量技术的影响、测量人员的心理影响等等随机因素叠加而成的,所以测量误差常认为服从正态分布。
(3)关于参数,μσ:μ是正态分布的的数学期望,即()E X μ=,称μ为正态分布的位置参数。
μ为正态分布的对称中心,在μ的左侧和()p x 下的面积为0.5;在μ的右侧和()p x 下的面积也是0.5,所以μ也是正态分布的中位数。
2σ是正态分布的方差,即2().Var X σ=σ是正态分布的标准差,σ愈小,正态分布愈集中,σ愈大,正态分布愈分散。
σ又称为是正态分布的的尺度参数。
(4)称0,1μσ==时的正态分布(0,1)N 为标准正态分布。
记U 为标准正态分布变量,()u ϕ和()u Φ为标准正态分布的密度函数和分布函数。
()u ϕ和()u φ满足:()()()();1.u u u u ϕϕ-=Φ-=-Φ(5)标准化变换:若()2~,,X N μσ则()~0,1.X U N μσ-=(6)若()2~,,X N μσ则对任意实数a 与b ,有()(),()1(),()()(),b P X b a P a X b a P a X b μσμσμμσσ-≤=Φ-<=-Φ--<≤=Φ-Φ0.6826,1,()()()0.9545,2,.0.9973, 3.k P X k k k k k μσ=⎧⎪-<=Φ-Φ-==⎨⎪=⎩(7)特征函数 22()exp{}.2t t i t σϕμ=-(标准正态分布2()exp{}2t t ϕ=-)1.2.均匀分布(1)若X 的密度函数和分布函数分别为1().0a x b P x b a else ⎧<<⎪=-⎨⎪⎩ 0,,(),.1,.x a x a F x a x b b a x b <⎧⎪-⎪=≤<⎨-⎪≥⎪⎩ 则称X 服从区间(,)a b 上的均匀分布,记作()~,.X U a b(2)背景:向区间(,)a b 随机投点,落点坐标X 一定服从均匀分布(),.U a b(3)()2(),().212b a a b E X Var X -+==(4)特征函数().()itb itae e t b a itϕ-=- 1.3. 指数分布(1)若X 的密度函数和分布函数分别为,0,()0,.x e x P x else λλ-⎧≥=⎨⎩ 1,0,().0,.x e x F x else λ-⎧-≥=⎨⎩ 则称X 服从指数分布,记作()~,X Exp λ其中参数0.λ>(2)背景:若一个元器件(或一台设备、或一个系统)遇到外来冲击时即告失败,则首次冲击到来的时间X (寿命)服从指数分布,很多产品的寿命可认为服从或者近似服从指数分布。




连续型随机变量的分布与应用连续型随机变量是概率论与数理统计中重要的研究对象之一,它与离散型随机变量相辅相成,被广泛应用于各个领域。
本文将探讨连续型随机变量的分布特性以及在实际问题中的应用。
一、连续型随机变量的定义与性质连续型随机变量是在一定范围内取任意实数值的随机变量。
与离散型随机变量不同,连续型随机变量的取值可以是实数区间内的任意一个点,且其概率密度函数可用来描述其分布特性。
1. 概率密度函数对于连续型随机变量X,其概率密度函数f(x)满足以下两个性质:(1)非负性:对于任意x,有f(x) ≥ 0;(2)归一性:∫f(x)dx = 1。
2. 分布函数连续型随机变量的分布函数F(x)定义为X ≤ x的概率,即F(x) =P(X ≤ x)。
由于连续型随机变量无论取任何具体值的概率都是0,因此F(x)可用概率密度函数进行求解。
二、常见的连续型随机变量分布在概率论与数理统计中,涉及到很多形式不同的连续型随机变量分布。
下面介绍几种常见的分布类型及其特点。
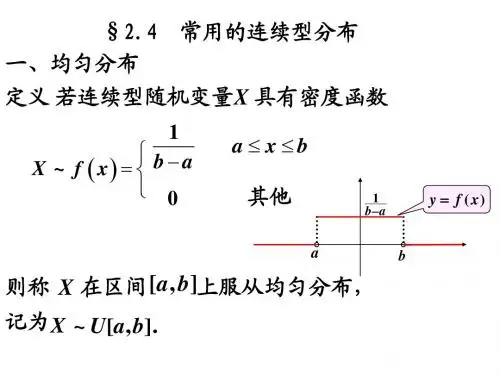
1. 均匀分布均匀分布是最简单的连续型随机变量分布之一,它在给定区间上的密度函数是常数。
均匀分布常用于模拟实验、随机抽样等场景。
2. 正态分布正态分布,又称高斯分布,是自然界中许多现象的分布模型。
它以其钟形曲线而著名,均值、方差是正态分布的两个重要参数。
正态分布在统计推断、假设检验等方面有广泛的应用。
3. 指数分布指数分布广泛应用于描述一些事件的持续时间或间隔时间,如设备寿命、电话呼叫等。
它具有无记忆性质,也就是说未来的发生与过去无关,仅与当前时刻有关。
4. 泊松分布泊松分布适用于描述单位时间(或单位面积、单位长度等)内某事件发生的次数的概率分布。
泊松分布常用于描述到达某一地点的车辆数、电话呼叫数等。
5. 威布尔分布威布尔分布常用于描述产品寿命或可靠性的分布。
它是指数分布的一般形式,通过加入形状参数来调整分布的形态。
三、连续型随机变量在实际问题中的应用1. 风险分析连续型随机变量在风险分析中有着广泛的应用。


连续型分布函数连续型分布函数是概率论和数理统计中的一个重要概念,它描述了一个随机变量取某个值以下的概率。
在实际问题中,我们经常需要对连续型随机变量进行概率分析和统计推断。
本文将介绍连续型分布函数的定义、性质和常见的几种连续型分布函数。
一、连续型分布函数的定义连续型分布函数是指一个随机变量的取值范围是实数集,并且每一个实数都对应一个概率。
它可以表示为F(x),表示随机变量取值小于等于x的概率,即P(X≤x)。
1. F(x)是一个非递减的函数,即对于任意的a≤b,有F(a)≤F(b);2. F(x)的取值范围是[0,1],即0≤F(x)≤1;3. 当x趋于负无穷时,F(x)趋于0;当x趋于正无穷时,F(x)趋于1;4. F(x)是右连续的,即对于任意的x,有F(x+)=F(x);5. F(x)的变化是分段的,即在每个区间上是一个线性函数。
三、常见的连续型分布函数1. 均匀分布函数(Uniform Distribution Function)均匀分布函数是指随机变量在一定区间上的取值是等可能的,即每个取值的概率相等。
它的分布函数为:F(x) = (x-a)/(b-a),其中a为区间下限,b为区间上限。
2. 正态分布函数(Normal Distribution Function)正态分布函数是指随机变量满足正态分布的情况,也称为高斯分布。
它的分布函数没有解析表达式,通常用标准正态分布函数进行近似计算。
3. 指数分布函数(Exponential Distribution Function)指数分布函数是指随机变量满足指数分布的情况,它描述了事件发生的时间间隔。
它的分布函数为:F(x) = 1 - e^(-λx),其中λ为事件发生的速率参数。
4. 伽玛分布函数(Gamma Distribution Function)伽玛分布函数是指随机变量满足伽玛分布的情况,它常用于描述等待时间或寿命分布。
它的分布函数没有解析表达式,通常使用伽玛函数进行计算。

连续型随机变量的分布函数引言连续随机变量是概率论中的重要概念之一,其取值范围是一段连续的实数区间。
与离散型随机变量不同,连续型随机变量的分布函数是一个实函数,描述了随机变量取值小于等于某一实数的概率。
本文将介绍连续型随机变量的分布函数的定义、性质以及常见的连续分布函数。
一、连续型随机变量的分布函数定义在概率论中,对于一维连续型随机变量X,其分布函数F(x)定义为:F(x) = P(X ≤ x)其中P为概率函数,表示X取值小于等于x的概率。
分布函数F(x)具有以下性质:1.F(x)是自变量x的单调不减函数;2.F(x)的取值范围是[0,1],即0≤F(x)≤1;3.当x→负无穷时,F(x)→0;当x→正无穷时,F(x)→1。
二、连续型随机变量的概率密度函数对于连续型随机变量X,其概率密度函数f(x)是分布函数F(x)的导数,即:f(x) = dF(x)/dx概率密度函数描述了连续型随机变量在不同取值下的概率密度。
概率密度函数具有以下性质:1.f(x)是非负函数,即对于所有x,有f(x)≥0;2.连续型随机变量所有可能取值的概率密度函数在取值范围上的积分等于1,即∫f(x)dx = 1。
通过概率密度函数可以计算出在某个区间内连续型随机变量的取值概率,即概率密度函数在该区间上的积分。
三、常见的连续分布函数1. 均匀分布(Uniform Distribution)均匀分布是一种简单的连续型随机变量分布,其概率密度函数在一个区间内全等于常数,即:f(x) = 1/(b-a),a≤x≤b,否则 f(x) = 0其中a和b是区间的上下界。
均匀分布的分布函数是线性的,在区间[a,b]内为0,在区间左侧小于a时为0,在区间右侧大于b时为1。
均匀分布的期望值为(a+b)/2,方差为(b-a)²/12。
2. 正态分布(Normal Distribution)正态分布是最具代表性的连续型随机变量分布之一,也称为高斯分布。
常用的连续概率分布如下:(1)正态分布。
其特点是密度函数以均值为中心对称分布,这是一种最常用的概率分布,其均值为,方差为,用表示。
当,时,称为标准正态分布,用N(0,1)表示。
正态分布适用于描述一般经济变量的概率分布,如销售量、售价、产品成本等。
(2)三角型分布。
其特点是密度数是由最大值、最可能值和最小值构成的对称的或不对称的三角型。
适用描述工期、投资等不对称分布的输入变量,也可用于描述产量、成本等对称分布的变量。
(3)β分布。
其特点是密度函数为在最大值两边不对称分布,适用于描述工期等不对称分布的变量。
(4)经验分布。
其密度函数并不适合于某些标准的概率函数,要根据统计资料及主观经验估计的非标准概率分布,它适合于项目评价中的所有各种变量。
(5)指数分布。
指数分布可以用来表示独立随机事件发生的时间间隔,比如旅客进机场的时间间隔、无线电元器件寿命等等。
指数分布的一个重要特征是无记忆性(Memoryless Property,又称遗失记忆性)。
阅读(354)| 评论(0)。
常用连续型分布性质汇总及其关系1. 常用分布 1.1 正态分布(1)若X 的密度函数和分布函数分别为()()()22222(),.,.x t xp x x F x edt x μσμσ-----∞=-∞<<+∞=-∞<<+∞则称X 服从正态分布,记作()2~,,X N μσ,其中参数,0.μσ-∞<<+∞> (2)背景:一个变量若是由大量微小的、独立的随机因素的叠加结果,则此变量一定是正态变量。
测量误差就是由量具零点偏差、测量环境的影响、测量技术的影响、测量人员的心理影响等等随机因素叠加而成的,所以测量误差常认为服从正态分布。
(3)关于参数,μσ:μ是正态分布的的数学期望,即()E X μ=,称μ为正态分布的位置参数。
μ为正态分布的对称中心,在μ的左侧和()p x 下的面积为0.5;在μ的右侧和()p x 下的面积也是0.5,所以μ也是正态分布的中位数。
2σ是正态分布的方差,即2().Var X σ=σ是正态分布的标准差,σ愈小,正态分布愈集中,σ愈大,正态分布愈分散。
σ又称为是正态分布的的尺度参数。
(4)称0,1μσ==时的正态分布(0,1)N 为标准正态分布。
记U 为标准正态分布变量,()u ϕ和()u Φ为标准正态分布的密度函数和分布函数。
()u ϕ和()u φ满足:()()()();1.u u u u ϕϕ-=Φ-=-Φ(5)标准化变换: 若()2~,,X N μσ则()~0,1.X U N μσ-=(6)若()2~,,X N μσ则对任意实数a 与b ,有()(),()1(),()()(),b P X b a P a X b a P a X b μσμσμμσσ-≤=Φ-<=-Φ--<≤=Φ-Φ0.6826,1,()()()0.9545,2,.0.9973, 3.k P X k k k k k μσ=⎧⎪-<=Φ-Φ-==⎨⎪=⎩(7)特征函数 22()exp{}.2t t i t σϕμ=-(标准正态分布2()exp{}2t t ϕ=-)1.2.均匀分布(1)若X 的密度函数和分布函数分别为1().0a xb P x b aelse⎧<<⎪=-⎨⎪⎩ 0,,(),.1,.x a x a F x a x b b a x b <⎧⎪-⎪=≤<⎨-⎪≥⎪⎩ 则称X 服从区间(,)a b 上的均匀分布,记作()~,.X U a b(2)背景:向区间(,)a b 随机投点,落点坐标X 一定服从均匀分布(),.U a b(3)()2(),().212b a a bE X Var X -+==(4)特征函数().()itb itae e t b a itϕ-=-1.3. 指数分布(1)若X 的密度函数和分布函数分别为,0,()0,.x e x P x else λλ-⎧≥=⎨⎩ 1,0,().0,.x e x F x else λ-⎧-≥=⎨⎩ 则称X 服从指数分布,记作()~,X Exp λ其中参数0.λ>(2)背景:若一个元器件(或一台设备、或一个系统)遇到外来冲击时即告失败,则首次冲击到来的时间X (寿命)服从指数分布,很多产品的寿命可认为服从或者近似服从指数分布。
(3)211(),().E X Var X λλ==(4)指数分布的无记忆性:若()~,X Exp λ则对任意0,0,s t >>有(|)().P X s t X s P X t >+>=>(5)特征函数1()1.it t ϕλ-⎛⎫=- ⎪⎝⎭1.4 伽玛分布(1)伽玛函数 称10()x x e dx αα+∞--Γ=⎰为伽玛函数,其中参数0.α>伽玛分布具有如下性质:(a )(1)1;Γ= (b) 1()2Γ= (c) (1)();αααΓ+=Γ(d) (1)()!n n n n Γ+=Γ=(n 为自然数)。
(2)伽玛分布 若X 的密度函数为1,0,().()0xx e x p x else ααλλα--⎧≥⎪=Γ⎨⎪⎩则称X 服从伽玛分布,记作~(,),X Ga αλ其中0.α>为形状参数,0λ>为尺度参数。
(3)背景:若一个元器件(或一台设备、或一个系统)能抵挡一些外来冲击,但遇到第k 次冲击时即告失败,则第k 次冲击来到的时间X (寿命)服从形状参数为k 的伽玛分布~(,).X Ga k λ(4)2(),().E X Var X ααλλ==(5)特征函数()1.it t αϕλ-⎛⎫=- ⎪⎝⎭1.5 贝塔分布(1)贝塔函数 称1110(,)(1)b a B a b x x dx --=-⎰为贝塔函数,其中参数0,a >0.b >贝塔函数具有如下性质: (a )(),(,);B a b B b a = (b) ()()(),.()a b B a b a b ΓΓ=Γ+(2) 贝塔分布 若X 的密度函数为11()(1),01,()()().0a b a b x x x b p x else α--Γ+⎧-<<⎪ΓΓ=⎨⎪⎩则称X 服从贝塔分布,记作~(,),X Be a b 其中0,a >0.b >都是形状参数。
(3)背景 很多比率,如产品的不合格率、机器的维修率、某商品的市场占有率、射击的命中率等都是在区间(0,1)上取值的随机变量,贝塔分布(,)Be a b 可供描述这些随机变量之用。
(4)()2(),.()(1)a ab E X D X a b a b a b ==++++ (5)特征函数0()()()().()()()(1)jj a b a j it t a b a b j j ϕ+∞=Γ+Γ+=ΓΓΓ++Γ+∑ 1.6 Z 分布(1)若X 的密度函数为()1()()0.()()1a a ba b x P x x a b x -+Γ+=≥ΓΓ+则称X 服从Z 分布,记作~(,),Z Z a b 其中0,a >0.b >都是形状参数。
(2)2(1)(),1,(), 2.1(1)(2)aa ab E X b Var X b b b b +-=>=>--- (3)若~(,),X Z a b 则1~(,).X Z b a2. 分布之间的关系2.1 由标准正态分布构造2χ-分布设1,...n x x 和1,...n y y 是来自标准正态分布的两个相互独立的样本, (1)221ni i x χ==∑ 服从自由度为n 的卡方分布,记为22~()n χχ。
其分布密度为12221()(0).()22n y n p y y e y n --=>Γ(2 ) 期望方差分别为()()222.E n Var n χχ==(3)特征函数为2()(12).n t it ϕ-=-2.2 由标准正态分布和卡方分布构造t 分布 (1)t =服从自由度为n 的t 分布,记为~().t t n 其分布密度为12212()(1)().()2n n y p y y n n +-+⎛⎫Γ ⎪⎝⎭=+-∞<<+∞ (2)期望方差分别()()0(1)(2).2nE t n Var t n n =>=>- (3)特征函数2.3 由两个卡方分布构造F 分布(1)()221221/()m n y y m F x x n+=++ 服从第一自由度为m ,第二自由度n 为的F分布,记为~(,).F F m n 其分布密度为21222()(1)().()()22m m m nm n m m n p y yy y m n n+--+⎛⎫⎛⎫Γ ⎪⎪⎝⎭⎝⎭=-+-∞<<+∞ΓΓ(2)期望方差分别()()222(2)(2)(4).2(2)(4)nn mn E F n V a rF nn m n n+-=>=>---(3)特征函数为(4)若~(,),F F m n 则1~(,).F F n m (5)若~(),t t n 则2~(1,).t F n 2.4 伽玛分布,贝塔分布及其特例(1)1α=时的伽玛分布就是指数分布,即(1,)().Ga Exp λλ=(2)2,12n αλ==时的伽玛分布为自由度为n 的2χ分布,即21(,)().22n Ga n χ= (3)1a b ==时的贝塔分布就是区间(0,1)上的均匀分布,即(1,1)(0,1).Be U = (4)12,,n x x x 独立同分布于()0,1U ,(1)(2)(),,n x x x 为其顺序统计量,则有()~(,1),1,2,.k x Be k n k k n -+=特别地,(1)~(1,),~(,1).n x B e n x B en()()~(,1),1,2,.k s x x Be k s n k s k s n ---++>= 特别地()(1)~(1,2).n x x Be n --(5)若随机变量~(,),X Ga αλ则当0k >时,有~(,).Y kX Ga k αλ=特别地,()22~(,12)2.X Ga λαχα=即任一伽玛分布可转化为2χ分布。
(6)若~(,)X Be a b ,则1~(,).X Be b a -(7)若1122~(,),~(,)X Ga X Ga αλαλ且12,X X 与相互独立,则1212~(,);X X Ga ααλ++11212~(,).X Be X X αα+ (8)Z 分布与贝塔分布,F 分布的关系 若~(,),X Be a b 则(1)~(,);Y X X Z a b =- 若~(,),X Z a b 则(1)~(,).Y X X Be a b =+ 若12~(2,2),X Z n n 则2121~(,).n Y X F n n n =。