连续型随机变量常见的几种分布

1.均匀分布 密度分布函数 ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<<-=其他,0,1)(b x a a b x f2.指数分布 密度分布函数 ⎭⎬⎫⎩⎨⎧>=-其他,00,)(x e x f x λλ 3.伽玛分布 密度分布函数 ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤>Γ=--0,00,)()(1x x e x x f x ααααλ4.正态分布 密度分布函数 222)(21)(σμπσ--=x e x f5.对数正态分布 密度分布函数 ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧>=--e l s e x e x x f x ,00,21)(222)(l n σμπσ6.贝塔分布 密度分布函数 ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<<-ΓΓ+Γ=--e l s e x x x r r r r x f r r ,010,)1()()()()(112121217.爱尔兰分布 密度分布函数 ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤>-=--0,00,)!1()(1x x e x r x f x r r λλ8.拉普拉斯分布 密度分布函数 ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=--λμλx e x f 21)(%泊松分布概率密度作图：x=0:20;y1=poisspdf(x,2.5);y2=poisspdf(x,5);y3=poisspdf(x,10);hold onplot(x,y1,':r*')plot(x,y2,':b*')plot(x,y3,':g*')hold offtitle('Poisson 分布')正态分布标准差意义的图示mu=3; sigma=0.5;x=mu+sigma*[-3:-1,1:3];yf=normcdf(x,mu,sigma);P=[yf(4)-yf(3),yf(5)-yf(2),yf(6)-yf(1)];xd=1:0.1:5;yd=normpdf(xd,mu,sigma);%for k=1:3xx{k}=x(4-k):sigma/10:x(3+k);yy{k}=normpdf(xx{k},mu,sigma);endsubplot(1,3,1),plot(xd,yd,'b');hold onfill([x(3),xx{1},x(4)],[0,yy{1},0],'g')text(mu-0.5*sigma,0.3,num2str(P(1))),hold offsubplot(1,3,2),plot(xd,yd,'b');hold onfill([x(2),xx{2},x(5)],[0,yy{2},0],'g')text(mu-0.5*sigma,0.3,num2str(P(2))),hold offsubplot(1,3,3),plot(xd,yd,'b');hold onfill([x(1),xx{3},x(6)],[0,yy{3},0],'g')text(mu-0.5*sigma,0.3,num2str(P(3))),hold offv=4;xi=0.9;x_xi=chi2inv(xi,v);x=0:0.1:15;yd_c=chi2pdf(x,v);%。

概率论连续型随机变量概率论是数学的一个分支，主要研究随机现象的概率规律和统计规律。

在概率论中，随机变量是一种可以随机取不同值的变量。

连续型随机变量是指取值范围为连续的变量，其概率分布函数可以用密度函数来描述。

连续型随机变量的概率密度函数（Probability Density Function，简称PDF）是描述随机变量取值概率的函数。

对于一个连续型随机变量X，其概率密度函数f(x)满足以下两个条件：1）f(x)≥0，对于所有的x；2）∫f(x)dx=1，即概率密度函数在整个取值范围上的积分等于1。

概率密度函数的性质决定了连续型随机变量的一些特点。

首先，连续型随机变量的概率是通过对其概率密度函数进行积分得到的。

例如，对于一个连续型随机变量X，其取值在[a,b]之间的概率可以表示为P(a≤X≤b)=∫f(x)dx。

其次，连续型随机变量的概率密度函数可以用来计算随机变量落在某个区间的概率。

例如，对于一个连续型随机变量X，可以计算P(X≥a)=∫f(x)dx。

对于连续型随机变量，我们也可以计算其期望值和方差。

连续型随机变量X的期望值E(X)表示随机变量的平均取值，可以通过对X乘以其概率密度函数f(x)后积分得到。

方差Var(X)表示随机变量取值的离散程度，可以通过计算E((X-E(X))^2)得到。

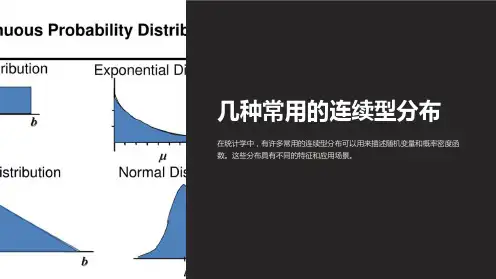
连续型随机变量常见的概率分布有正态分布、指数分布、均匀分布等。

其中，正态分布是最重要的连续型概率分布之一。

正态分布的概率密度函数是一个钟形曲线，其均值和标准差决定了曲线的位置和形状。

正态分布在自然界和社会科学中都有广泛的应用，如身高、体重、考试成绩等。

指数分布是描述事件发生时间间隔的概率分布。

指数分布的概率密度函数是单峰递减的曲线，其形状由参数λ决定。

指数分布在可靠性工程、排队论、风险分析等领域有广泛应用。

均匀分布是描述随机变量在一个区间内取值的概率分布。

均匀分布的概率密度函数是一个常数，区间内所有取值的概率相等。

连续型概率分布连续型概率分布是概率论中的一个重要概念，用于描述连续随机变量的可能取值范围及其对应的概率。

与离散型概率分布相比，连续型概率分布在数轴上的每一个点都有概率密度函数与之对应，而不是直接给出某个点的概率。

本文将介绍几种常见的连续型概率分布，包括均匀分布、正态分布和指数分布。

一、均匀分布均匀分布是一种简单而常见的连续型概率分布，它假设随机变量在一定的范围内取值的概率是相同的。

在数学上，均匀分布的概率密度函数为：f(x) = 1 / (b - a)，a ≤ x ≤ b其中，a和b分别表示均匀分布的下界和上界。

图表上，均匀分布的概率密度函数在[a, b]区间内的取值是一个常数，且在[a, b]之外为0。

这意味着在[a, b]区间内的任意一个子区间上，概率密度的积分就是该子区间的长度除以[a, b]之间的总长度。

二、正态分布正态分布是统计学中最重要的连续型概率分布之一，也被称为高斯分布。

正态分布在自然界和社会科学中的广泛应用使得它成为了研究的重点。

正态分布的概率密度函数可以写作：f(x) = 1 / (σ * √(2π)) * exp(-(x - μ)² / (2σ²))其中，μ是均值，σ是标准差。

正态分布的概率密度函数呈钟形曲线，其峰值位于μ处，标准差决定了曲线的形状。

正态分布具有许多重要的特性，如68-95-99.7法则，即大约68%的概率密度位于一个标准差范围内，95%位于两个标准差范围内，99.7%位于三个标准差范围内。

三、指数分布指数分布是描述连续随机事件发生的时间间隔的概率分布。

例如，某个服务台上的顾客到达时间间隔、两次地震发生的间隔等，都可以用指数分布来描述。

指数分布的概率密度函数可以写作：f(x) = λ * exp(-λx)，x ≥ 0其中，λ是分布的参数，表示单位时间内事件发生的平均次数。

指数分布的概率密度函数在区间[0, +∞)上递减，且总面积等于1。

指数分布还有一个重要的特性是无记忆性，即已经等待了一段时间后，再等待一段时间的概率与一开始等待这段时间的概率是相等的。

连续型分布函数连续型分布函数是概率论和数理统计中的一个重要概念，它描述了一个随机变量取某个值以下的概率。

在实际问题中，我们经常需要对连续型随机变量进行概率分析和统计推断。

本文将介绍连续型分布函数的定义、性质和常见的几种连续型分布函数。

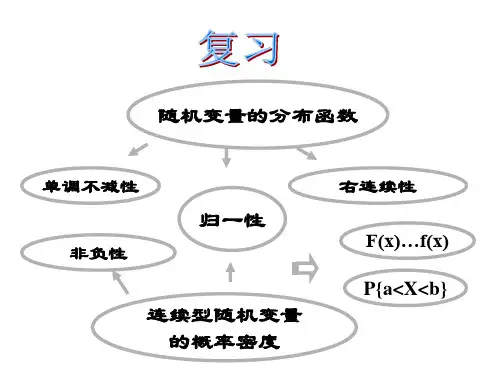
一、连续型分布函数的定义连续型分布函数是指一个随机变量的取值范围是实数集，并且每一个实数都对应一个概率。

它可以表示为F(x)，表示随机变量取值小于等于x的概率，即P(X≤x)。

1. F(x)是一个非递减的函数，即对于任意的a≤b，有F(a)≤F(b)；2. F(x)的取值范围是[0,1]，即0≤F(x)≤1；3. 当x趋于负无穷时，F(x)趋于0；当x趋于正无穷时，F(x)趋于1；4. F(x)是右连续的，即对于任意的x，有F(x+)=F(x)；5. F(x)的变化是分段的，即在每个区间上是一个线性函数。

三、常见的连续型分布函数1. 均匀分布函数（Uniform Distribution Function）均匀分布函数是指随机变量在一定区间上的取值是等可能的，即每个取值的概率相等。

它的分布函数为：F(x) = (x-a)/(b-a)，其中a为区间下限，b为区间上限。

2. 正态分布函数（Normal Distribution Function）正态分布函数是指随机变量满足正态分布的情况，也称为高斯分布。

它的分布函数没有解析表达式，通常用标准正态分布函数进行近似计算。

3. 指数分布函数（Exponential Distribution Function）指数分布函数是指随机变量满足指数分布的情况，它描述了事件发生的时间间隔。

它的分布函数为：F(x) = 1 - e^(-λx)，其中λ为事件发生的速率参数。

4. 伽玛分布函数（Gamma Distribution Function）伽玛分布函数是指随机变量满足伽玛分布的情况，它常用于描述等待时间或寿命分布。

它的分布函数没有解析表达式，通常使用伽玛函数进行计算。

第七讲连续型随机变量（续）及随机变量的函数的分布3. 三种重要的连续型随机变量 （1）均匀分布设连续型随机变量X 具有概率密度)5.4(,,0,,1)(⎪⎩⎪⎨⎧<<-=其它b x a ab x f则称X 在区间(a,b)上服从均匀分布, 记为X~U(a,b).X 的分布函数为)6.4(.,1,,,,0)(⎪⎪⎩⎪⎪⎨⎧≥<≤--<=b x b x a a b a x a x x F（2）指数分布设连续型随机变量X 的概率密度为)7.4(,,0,0,e1)(/⎪⎩⎪⎨⎧>=-其它x x f x θθ其中θ>0为常数, 则称X 服从参数为θ的指数分布.容易得到X 的分布函数为第二章 随机变量及其分布§4 连续型随机变量及其概率密度=2)8.4(.,0,0,1)(/⎩⎨⎧>-=-其它x e x F x θ如X 服从指数分布, 则任给s,t>0, 有 P{X>s+t | X > s}=P{X > t} (4.9)事实上}.{e ee)(1)(1}{}{}{)}(){(}|{//)(t X P s F t s F s X P t s X P s X P s X t s X P s X t s X P t s t s >===-+-=>+>=>>⋂+>=>+>--+-θθθ性质(4.9)称为无记忆性.指数分布在可靠性理论和排队论中有广泛的运用. （3）正态分布设连续型随机变量X 的概率密度为)10.4(,,e21)(222)(∞<<-∞=--x x f x σμσπ其中μ,σ(σ>0)为常数, 则称X 服从参数为μ,σ的正态分布或高斯(Gauss)分布, 记为X~N(μ,2σ).显然f(x)≥0, 下面来证明1d )(=⎰+∞∞-x x f令t x =-σμ/)(, 得到dx edx et x 22)(2222121-∞+∞---∞+∞-⎰⎰=πσπσμf (x )的图形:1.5.1d 21d 21)11.4(π2d d e,,d d ,d e22)(20222/)(22/2222222======⎰⎰⎰⎰⎰⎰⎰∞∞--∞∞---∞-+∞∞-+∞∞-+-∞∞--x ex e r r I u t e I t I t x r u tt πσπθσμπ于是得转换为极坐标则有记f(x)具有的性质:（1）.曲线关于x=μ对称. 这表明对于任意h>0有P{μ-h<X ≤μ}=P{μ<X ≤μ+h}. （2）.当x=μ时取到最大值.π21)(σμ=f x 离μ越远, f(x)的值越小. 这表明对于同样长度的区间, 当区间离μ越远, X 落在这个区间上的概率越小。

连续型随机变量的分布函数引言连续随机变量是概率论中的重要概念之一，其取值范围是一段连续的实数区间。

与离散型随机变量不同，连续型随机变量的分布函数是一个实函数，描述了随机变量取值小于等于某一实数的概率。

本文将介绍连续型随机变量的分布函数的定义、性质以及常见的连续分布函数。

一、连续型随机变量的分布函数定义在概率论中，对于一维连续型随机变量X，其分布函数F(x)定义为：F(x) = P(X ≤ x)其中P为概率函数，表示X取值小于等于x的概率。

分布函数F(x)具有以下性质：1.F(x)是自变量x的单调不减函数；2.F(x)的取值范围是[0,1]，即0≤F(x)≤1；3.当x→负无穷时，F(x)→0；当x→正无穷时，F(x)→1。

二、连续型随机变量的概率密度函数对于连续型随机变量X，其概率密度函数f(x)是分布函数F(x)的导数，即：f(x) = dF(x)/dx概率密度函数描述了连续型随机变量在不同取值下的概率密度。

概率密度函数具有以下性质：1.f(x)是非负函数，即对于所有x，有f(x)≥0；2.连续型随机变量所有可能取值的概率密度函数在取值范围上的积分等于1，即∫f(x)dx = 1。

通过概率密度函数可以计算出在某个区间内连续型随机变量的取值概率，即概率密度函数在该区间上的积分。

三、常见的连续分布函数1. 均匀分布（Uniform Distribution）均匀分布是一种简单的连续型随机变量分布，其概率密度函数在一个区间内全等于常数，即：f(x) = 1/(b-a)，a≤x≤b，否则 f(x) = 0其中a和b是区间的上下界。

均匀分布的分布函数是线性的，在区间[a,b]内为0，在区间左侧小于a时为0，在区间右侧大于b时为1。

均匀分布的期望值为(a+b)/2，方差为(b-a)²/12。

2. 正态分布（Normal Distribution）正态分布是最具代表性的连续型随机变量分布之一，也称为高斯分布。