12级高二数学零诊复习讲义2.3练习及答案

2011—2013届成都高中毕业班摸底试题分类解析（二）考点七：离子浓度大小的比较1、（2009、零诊）下列说法不正确．．．的是（）A．100 ℃时，纯水中c（H +）＝1 ×10－6mol · L－1, pH 小于7 ，此时纯水显酸性B．pH＝12 的烧碱和氢氧化钡溶液，二者物质的量浓度之比为2 : 1C．pH ＝的盐酸与pH ＝5 的硫酸等体积混合，pH ＝3 . 3D．0 . 1 mol · L－1 CH3COOH 溶液中，c ( CH3COOH ) ＞c（CH3COO一）2、（2009、零诊）已知某温度下，K w＝l×10－13。

A 为酸溶液，其pH ＝a；B 为碱溶液，其pH ＝b 。

（l）若A 为强酸，B 为强碱，且a + b ＝13 ，两者等体积混合后，溶液的pH ＝_________________；若此时溶液中阳离子浓度大于阴离子浓度，其原因可能是（用文字表述）___________________________________________________________ （2）若A 的化学式为HR, B的化学式为MOH ，且a + b ==3 。

若两者等体积混合后溶液显碱性，则其原因可能是_________________________________________，此混合后的溶液中，微粒浓度大小关系一定正确的是_______________填序号）。

① c（MOH ）> c ( M + ) > c ( R一)> c ( H + ) > c ( OH一)② c ( HR ) > c ( M + ) > c ( R一)> c ( OH一)> c ( H + )③ c（M +）> c ( R一)> c ( H + ) > c ( OH一)④ c ( M + ) > c ( R一)> c ( OH一)＞c（H +）⑤ c ( M + ) + c ( H + ) == c ( R 一)+ c ( OH一)⑥ c ( MOH ) == c (H +)一c（OH一）3．（2010、零诊）物质的量浓度各为0.1 mol·L－CH3COOH 和CH3COONa溶液等体积混合后，溶液呈酸性。

高中数学学习材料马鸣风萧萧*整理制作成都七中2012届高二“零诊”复习讲义 2.4 数列通项公式与求和第二讲 数列与不等式 2.4 数列通项公式与求和姓名________________ 班级______ 【知识网络】一、数列的通项的求法：1、公式法：①等差数列通项公式；②等比数列通项公式；2、已知n S （即12()n a a a f n +++=）求n a ，用作差法：{11,(1),(2)n n n S n a S S n -==-≥；3、已知12()n a a a f n =求n a ，用作商法：(1),(1)(),(2)(1)n f n f n a n f n =⎧⎪=⎨≥⎪-⎩；4、若1()n n a a f n +-=求n a 用累加法：11221()()()n n n n n a a a a a a a ---=-+-++-1a +(2)n ≥；5、已知1()n n a f n a +=求n a ，用累乘法：121121n n n n n a a aa a a a a ---=⋅⋅⋅⋅(2)n ≥；6、已知递推关系求n a ，用构造法（构造等差、等比数列）．⑴形如1n n a ka b -=+、1nn n a ka b -=+（,k b 为常数）的递推数列都可以用待定系数法转化为公比为k 的等比数列后，再求n a ； ⑵形如11n n n a a ka b--=+的递推数列都可以用倒数法求通项．二、数列求和的常用方法：1、公式法：①等差数列求和公式；②等比数列求和公式，特别声明：运用等比数列求和公式，务必检查其公比与1的关系，必要时需分类讨论； ③常用公式：1123(1)2n n n ++++=+，222112(1)(21)6n n n n +++=++，33332(1)123[]2n n n +++++=. 2、分组求和法：在直接运用公式法求和有困难时，常将“和式”中“同类项”先合并在一起，再运用公式法求和； 3、倒序相加法：若和式中到首尾距离相等的两项和有其共性或数列的通项与组合数相关联，则常可考虑选用倒序相加法，发挥其共性的作用求和（这也是等差数列前n 和公式推导方法）； 4、错位相减法：如果数列的通项是由一个等差数列的通项与一个等比数列的通项相乘构成，那么常选用错位相减法（这也是等比数列前n 和公式的推导方法）；5、裂项相消法：如果数列的通项可“分裂成两项差”的形式，且相邻项分裂后相关联，那么常选用裂项相消法求和.常用裂项形式有：①111(1)1n n n n =-++； ②1111()()n n k k n n k=-++； ③2211111()1211k k k k <=---+，211111111(1)(1)1k k k k k k k k k -=<<=-++--； ④1111[](1)(2)2(1)(1)(2)n n n n n n n =-+++++ ； ⑤11(1)!!(1)!n n n n =-++； ⑥2122(1)2(1)11n n n n n n n n n +-=<<=--+++-. 6、并项求和法：一个数列的前n 项和中，可两两结合求解，则称之为并项求和，形如()()1nn a f n =-类型可采用两项合并求解．【典型例题】考点1 已知递推公式求通项公式例1 ⑴已知111,32n n a a a -==+，则n a =____________．⑵已知111,32nn n a a a -==+，则n a =____________．⑶已知1111,31n n n a a a a --==+，则n a =____________．⑷已知数列满足11a =，11n n n n a a a a ---=，则n a =____________．考点2 公式法求和例2 ⑴等比数列{}n a 的前n 项和21n n S =-，则2232221n a a a a ++++ ＝____________；⑵计算机是将信息转换成二进制数进行处理的．二进制即“逢2进1”，如2)1101(表示二进制数，将它转换成十进制形式是13212021210123=⨯+⨯+⨯+⨯，那么将二进制120052)11111(个转换成十进制数是_____________；考点3 分组法求和例 3 已知数列{}n a 的通项公式为231nn a n =+-，则数列{}n a 的前n 项和n S =___________；考点4 倒序相加法求和例4 求和01235(21)n n n n n C C C n C +++++=_________________；考点5 错位相减法求和例5 已知数列{}n a 的前n 项和为n S ，()111,21n n a a S n N *+==+∈，等差数列{}n b 中，()0n b n N *>∈，且12315b b b ++=，又112233,,a b a b a b +++成等比数列．⑴求数列{}{},n n a b 的通项公式； ⑵求数列{}n n a b ⋅的前n 项和n T ．考点6 裂项相消法求和例6 已知数列{}n a 的各项均是正数，前n 项和为n S ，且满足()21n n p S p a -=-，其中p为正常数，且1p ≠．⑴求数列{}n a 的通项公式； ⑵设()12log n p nb n N a *=∈-，求数列{}1n n b b +的n 项和n T ； ⑶判断是否存在正整数M ，使得n M >时，1473278n a a a a a ->恒成立，若存在，求出相应的M 的最小值；若不存在，说明理由．考点7 并项求和法求和例7 求22222210099989721n S =-+-++-=_____________．【课时作业】1、已知数列{}n a 为等比数列，n S 是是它的前n 项和,若2312a a a ⋅=，且4a 与27a 的等差中项为54，则5S =( ) A ．35 B ．33 C ．3l D ．29 2、已知数列{}n a 是公差不为零的等差数列，且134,,a a a 成等比数列，n S 为数列{}n a 的前n 项和，则35S S =_______________. 3、已知数列{}n a 满足1133,2,n n a a a n +=-=则na n的最小值为__________. 4、已知数列{}n a 满足()()11,log 12,,n n a a n n n N *==+≥∈定义：使乘积12k a a a ⋅⋅⋅为正整数的()k k N *∈叫做和谐数，则在区间[]1,2011内所有的和谐数的和为___________. 5、已知数列{a n }满足a 1＝0，a 2＝2，且对任意m 、n ∈N *都有 a 2m －1＋a 2n －1＝2a m ＋n －1＋2(m －n )2. （Ⅰ）求a 3，a 5；（Ⅱ）设b n ＝a 2n ＋1－a 2n －1(n ∈N *)，证明：{b n }是等差数列；（Ⅲ）设c n ＝(a n+1－a n )q n －1(q ≠0，n ∈N *)，求数列{c n }的前n 项和S n .讲义答案。

高二数学课后练习题及答案高二数学课后练习题及答案选修2-2 1.1 第3课时导数的几何意义一、选择题1.如果曲线y=f(x)在点(x0，f(x0))处的切线方程为x+2y-3=0，那么()A.f(x0)0B.f(x0)0C.f(x0)=0D.f(x0)不存在[答案] B[解析] 切线x+2y-3=0的斜率k=-12，即f(x0)=-120.故应选B.2.曲线y=12x2-2在点1，-32处切线的倾斜角为()A.1B.4C.544[答案] B[解析] ∵y=limx0 [12(x+x)2-2]-(12x2-2)x=limx0 (x+12x)=x切线的斜率k=y|x=1=1.切线的倾斜角为4，故应选B.3.在曲线y=x2上切线的倾斜角为4的点是()A.(0,0)B.(2,4)C.14，116D.12，14[答案] D[解析] 易求y=2x，设在点P(x0，x20)处切线的倾斜角为4，则2x0=1，x0=12，P12，14.4.曲线y=x3-3x2+1在点(1，-1)处的切线方程为()A.y=3x-4B.y=-3x+2C.y=-4x+3D.y=4x-5[答案] B[解析] y=3x2-6x，y|x=1=-3.由点斜式有y+1=-3(x-1).即y=-3x+2.5.设f(x)为可导函数，且满足limx0 f(1)-f(1-2x)2x=-1，则过曲线y=f(x)上点(1，f(1))处的切线斜率为()A.2B.-1C.1D.-2[答案] B[解析] limx0 f(1)-f(1-2x)2x=limx0 f(1-2x)-f(1)-2x=-1，即y|x=1=-1，则y=f(x)在点(1，f(1))处的切线斜率为-1，故选B.6.设f(x0)=0，则曲线y=f(x)在点(x0，f(x0))处的切线()A.不存在B.与x轴平行或重合C.与x轴垂直D.与x轴斜交[答案] B[解析] 由导数的几何意义知B正确，故应选B.7.已知曲线y=f(x)在x=5处的切线方程是y=-x+8，则f(5)及f(5)分别为()A.3,3B.3，-1C.-1,3D.-1，-1[答案] B[解析] 由题意易得：f(5)=-5+8=3，f(5)=-1，故应选B.8.曲线f(x)=x3+x-2在P点处的切线平行于直线y=4x-1，则P点的坐标为()A.(1,0)或(-1，-4)B.(0,1)C.(-1,0)D.(1,4)[答案] A[解析] ∵f(x)=x3+x-2，设xP=x0，y=3x20x+3x0(x)2+(x)3+x，yx=3x20+1+3x0(x)+(x)2，f(x0)=3x20+1，又k=4，3x20+1=4，x20=1.x0=1，故P(1,0)或(-1，-4)，故应选A.9.设点P是曲线y=x3-3x+23上的任意一点，P点处的切线倾斜角为，则的取值范围为()A.0，23B.0，56C.23D.2，56[答案] A[解析] 设P(x0，y0)，∵f(x)=limx0 (x+x)3-3(x+x)+23-x3+3x-23x=3x2-3，切线的斜率k=3x20-3，tan=3x20-3-3.0，23.故应选A.10.(2016福州高二期末)设P为曲线C：y=x2+2x+3上的点，且曲线C在点P处切线倾斜角的取值范围为[0，4]，则点P横坐标的取值范围为()A.[-1，-12]B.[-1,0]C.[0,1]D.[12，1][答案] A[解析] 考查导数的几何意义.∵y=2x+2，且切线倾斜角[0，4]，切线的斜率k满足01，即01，-1-12.二、填空题11.已知函数f(x)=x2+3，则f(x)在(2，f(2))处的切线方程为________.[答案] 4x-y-1=0[解析] ∵f(x)=x2+3，x0=2f(2)=7，y=f(2+x)-f(2)=4x+(x)2yx=4+x.limx0 yx=4.即f(2)=4.又切线过(2,7)点，所以f(x)在(2，f(2))处的切线方程为y-7=4(x-2) 即4x-y-1=0.12.若函数f(x)=x-1x，则它与x轴交点处的切线的方程为________.[答案] y=2(x-1)或y=2(x+1)[解析] 由f(x)=x-1x=0得x=1，即与x轴交点坐标为(1,0)或(-1,0).∵f(x)=limx0 (x+x)-1x+x-x+1xx=limx0 1+1x(x+x)=1+1x2.切线的斜率k=1+11=2.切线的方程为y=2(x-1)或y=2(x+1).13.曲线C在点P(x0，y0)处有切线l，则直线l与曲线C的公共点有________个.[答案] 至少一[解析] 由切线的定义，直线l与曲线在P(x0，y0)处相切，但也可能与曲线部分有公共点，故虽然相切，但直线与曲线公共点至少一个.14.曲线y=x3+3x2+6x-10的切线中，斜率最小的切线方程为________.[答案] 3x-y-11=0[解析] 设切点P(x0，y0)，则过P(x0，y0)的切线斜率为，它是x0的函数，求出其最小值.设切点为P(x0，y0)，过点P的切线斜率k= =3x20+6x0+6=3(x0+1)2+3.当x0=-1时k有最小值3，此时P的坐标为(-1，-14)，其切线方程为3x-y-11=0.三、解答题15.求曲线y=1x-x上一点P4，-74处的切线方程.[解析] y=limx0 1x+x-1x-(x+x-x)x=limx0 -xx(x+x)-xx+x+xx=limx0 -1x(x+x)-1x+x+x=-1x2-12x .y|x=4=-116-14=-516，曲线在点P4，-74处的切线方程为：y+74=-516(x-4).即5x+16y+8=0.16.已知函数f(x)=x3-3x及y=f(x)上一点P(1，-2)，过点P作直线l.(1)求使直线l和y=f(x)相切且以P为切点的'直线方程;(2)求使直线l和y=f(x)相切且切点异于点P的直线方程y=g(x).[解析] (1)y=limx0 (x+x)3-3(x+x)-3x3+3xx=3x2-3.则过点P且以P(1，-2)为切点的直线的斜率k1=f(1)=0，所求直线方程为y=-2.(2)设切点坐标为(x0，x30-3x0)，则直线l的斜率k2=f(x0)=3x20-3，直线l的方程为y-(x30-3x0)=(3x20-3)(x-x0)又直线l过点P(1，-2)，-2-(x30-3x0)=(3x20-3)(1-x0)，x30-3x0+2=(3x20-3)(x0-1)，解得x0=1(舍去)或x0=-12.故所求直线斜率k=3x20-3=-94，于是：y-(-2)=-94(x-1)，即y=-94x+14.17.求证：函数y=x+1x图象上的各点处的切线斜率小于1.[解析] y=limx0 f(x+x)-f(x)x=limx0 x+x+1x+x-x+1xx=limx0 xx(x+x)-x(x+x)xx=limx0 (x+x)x-1(x+x)x=x2-1x2=1-1x21，y=x+1x图象上的各点处的切线斜率小于1.18.已知直线l1为曲线y=x2+x-2在点(1,0)处的切线，l2为该曲线的另一条切线，且l1l2.(1)求直线l2的方程;(2)求由直线l1、l2和x轴所围成的三角形的面积.[解析] (1)y|x=1=limx0 (1+x)2+(1+x)-2-(12+1-2)x=3，所以l1的方程为：y=3(x-1)，即y=3x-3.设l2过曲线y=x2+x-2上的点B(b，b2+b-2)，y|x=b=limx0 (b+x)2+(b+x)-2-(b2+b-2)x=2b+1，所以l2的方程为：y-(b2+b-2)=(2b+1)(x-b)，即y=(2b+1)x-b2-2.因为l1l2，所以3(2b+1)=-1，所以b=-23，所以l2的方程为：y=-13x-229.(2)由y=3x-3，y=-13x-229，得x=16，y=-52，即l1与l2的交点坐标为16，-52.又l1，l2与x轴交点坐标分别为(1,0)，-223，0.所以所求三角形面积S=12-521+223=12512.【高二数学课后练习题及答案】。

零诊复习资料（仅供7班使用） 第2讲 函数的性质【知识梳理】一、单调性1.定义：设D 是函数()f x 定义域的子区间，对任意12,x x D ∈，当12x x <时： (1) 都有()()12f x f x <⇔()f x 在区间D 上是增函数； (2) 都有()()12f x f x >⇔()f x 在区间D 上是减函数.2.判定：(1) 定义法；(2) 图象法：(3) 结论法(所学初等函数的单调性) ；3. 1.(1)(2)2.（23.1.2.1. ()f x 是周期函数，T 是它的一个周期.2.性质：(1) 若T 是()f x 的一个周期, 则(),0kT k Z k ∈≠也是()f x 的周期； (2) 若T 是()f x 的一个周期，则()fx ω ()0ω≠是周期函数，且一个周期是||ωT .3. 结论：(1)若()y f x =图象有两条对称轴,()x a x b a b ==≠，则()y f x =必是周期函数，且一周期为2||T a b =-；(2)若()y f x =图象有两个对称中心(,0),(,0)()A a B b a b ≠，则()y f x =是周期函数，且一周期为2||T a b =-；(3)如果函数()y f x =的图象有一个对称中心(,0)A a 和一条对称轴()x b a b =≠，则函数()y f x =必是周期函数，且一周期为4||T a b =-；(4)若函数()f x 满足下列条件之一, 则()f x 是周期函数,且一个周期为2T a =()0a ≠：①()()f a x f x +=-；②1()()f x a f x +=；③1()()f x a f x +=-.例2．(1) 若定义在R 上的奇函数()f x 以T 为周期，则函数()f x 在区间[,]T T -上至少有5 个零点.(2)函数()f x 的定义域为R ，若()1f x +和()1f x -都是奇函数，则函数()()g x f x =，{}1,1,3,5x ∈-的值域是 {}0.(3)定义在R 上的偶函数()f x 满足(2)()f x f x +=-，且在[6,4]--上是增函数，在锐角ABC ∆中，令(sin sin )m f A B =+，(cos cos )n f A C =+，则m 和n 的大小关系为_______ m n <.(4)函数()12sinf x x π=+在区间[]2,4-上的所有零点之和等于 8 .-1（1（22．点拨：y a =与log (0,1)a y x a a =>≠互为反函数，其图象关于y x =对称。

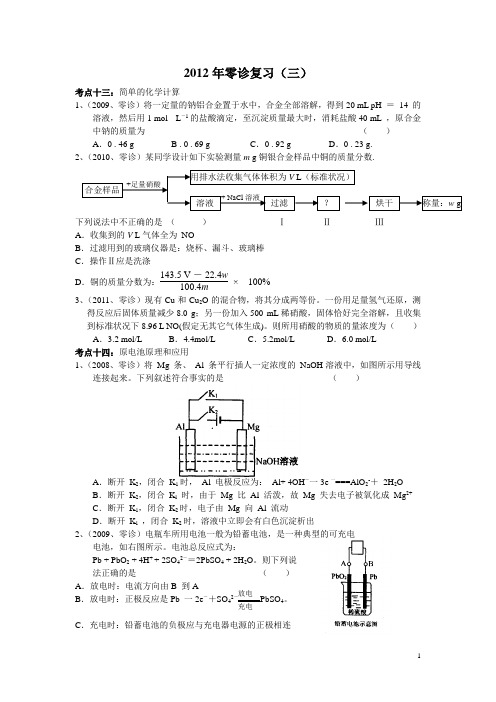
2012年零诊复习（三）考点十三：简单的化学计算1、（2009、零诊）将一定量的钠铝合金置于水中，合金全部溶解，得到20 mL pH ＝ 14 的溶液，然后用1 mol · L －1的盐酸滴定，至沉淀质量最大时，消耗盐酸40 mL ，原合金中钠的质量为 （ ）A ．0 . 46 gB . 0 . 69 gC ．0 . 92 gD ．0 . 23 g.2、（2010、零诊）某同学设计如下实验测量m g 铜银合金样品中铜的质量分数.下列说法中不正确的是 （ ）A ．收集到的V L 气体全为 NOB ．过滤用到的玻璃仪器是：烧杯、漏斗、玻璃棒C ．操作Ⅱ应是洗涤D ．铜的质量分数为：143.5 V － 22.4w 100.4m× 100% 3、（2011、零诊）现有Cu 和Cu 2O 的混合物，将其分成两等份。

一份用足量氢气还原，测得反应后固体质量减少8.0 g ；另一份加入500 mL 稀硝酸，固体恰好完全溶解，且收集到标准状况下8.96 L NO(假定无其它气体生成)。

则所用硝酸的物质的量浓度为（ ）A ．3.2 mol/LB ．4.4mol/LC ．5.2mol/LD ．6.0 mol/L考点十四：原电池原理和应用1、（2008、零诊）将 Mg 条、 Al 条平行插人一定浓度的 NaOH 溶液中，如图所示用导线连接起来。

下列叙述符合事实的是 （ ）A ．断开 K 2，闭合 K 1时， Al 电极反应为： Al+ 4OH －一3e 一===AlO 2-＋ 2H 2OB ．断开 K 2，闭合 K l 时，由于 Mg 比 Al 活泼，故 Mg 失去电子被氧化成 Mg 2+C ．断开 K 1，闭合 K 2时，电子由 Mg 向 Al 流动D ．断开 K l ，闭合 K 2时，溶液中立即会有白色沉淀析出2、（2009、零诊）电瓶车所用电池一般为铅蓄电池，是一种典型的可充电电池，如右图所示。

While <10End While开始n p <是输入p结束 输出S否12n S S =+ 1n n =+ 0,0n S ==2021年高二12月阶段测试 数学 含答案一、填空题（本大题共14小题,每小题5分,计70分） 1.命题“"xR ，sinx>0”的否定是___▲______2．复数(为虚数单位)的虚部是 ▲3.已知，若p 是q 的必要不充分条件，则的取值范围是 ▲4.执行右图语句后,打印纸上打印出的结果应是____▲______5.观察下列等式照此规律，第个等式为 ▲ 。

1=1 2+3+4=9 3+4+5+6+7=25 4+5+6+7+8+9+10=49……6．若双曲线的右焦点在抛物线的准线上，则实数的值为___▲． 7．执行右边的程序框图,若，,则输出的 ▲8．设定义在上的函数, 则不等式f (x −1)＋f (1−x 2)＜0的解集为 _ ▲____9．过抛物线的焦点的直线交抛物线于A 、B 两点，O 为坐标原点，则= ▲ . 10．命题：在上有意义，命题：函数 的定义域为．如果且为真命题，则的取值范围为 ▲ ．11. 已知函数在点处的切线为y =2x -1，则函数在点处的切线方程为 ▲ ． 12．对于函数，若存在区间，当时，的值域为(＞0），则称为倍值函数。

若是倍值函数，则实数的取值范围是 ▲ 13.已知椭圆：，点分别是椭圆的左顶点和左焦点，点 是圆上的动点.若是常数，则椭圆的离心率是 ▲14．已知函数23221()1(0)()31,()2(3)1(0)x x f x x x g x x x ⎧-+>⎪=-+=⎨⎪-++≤⎩，则方程（为正实数）的实数根最多有 ▲ 个二、解答题（本大题共6小题，计90分. 请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．）15.（文）已知.22:,0)6)(2(:,0m x m q x x p m +≤≤-≤-+> （1）若是的充分条件，求实数的取值范围； （2）若或为真命题，“且为假命题，求实数的取值范围.15.（理）如图，在棱长为3的正方体中，. ⑴求两条异面直线与所成角的余弦值； ⑵求平面与平面所成的锐二面角的余弦值.16.已知在处都取得极值． （1）求、的值；（2）若对时，恒成立，求实数的取值范围．17.张林在李明的农场附近建了一个小型工厂，由于工厂生产须占用农场的部分资源，因此李明每年向张林索赔以弥补经济损失并获得一定净收入．工厂在不赔付农场的情况下，工厂的年利润（元）与年产量（吨）满足函数关系．若工厂每生产一吨产品必须赔付农场元（以下称为赔付价格）．（1）将工厂的年利润（元）表示为年产量（吨）的函数，并求出工厂获得最大利润的年产量； （2）若农场每年受工厂生产影响的经济损失金额（元），在工厂按照获得最大利润的产量进行生产的前提下，农场要在索赔中获得最大净收入，应向张林的工厂要求赔付价格是多少？18.已知椭圆的左,右焦点分别为，其中也是抛物线的焦点，是与在第一象限的交点，且 （1）求椭圆的方程；（2）已知点是椭圆上一点，是椭圆上的两个动点，若直线的斜率与的斜率互为相反数，探求直线的斜率是否为定值？如果是，求出定值；反之，请说明理由.19.已知椭圆的离心率为，且经过点，若分别是椭圆的右顶点和上顶点，直线与AB 相交于点D ，与椭圆相交于E 、F 两点. （1）求椭圆的方程； （2）若，求的值；（3）求四边形面积的最大值．20.若函数在处的导数为，则称点为函数的驻点，若点(1,1)为函数f (x )的驻点，则称f (x )具有“1—1驻点性”.（1）设函数f (x )=，其中.①求证：函数f (x )不具有“1—1驻点性”；②求函数f (x )的单调区间.（2）已知函数g (x )=bx 3+3x 2+cx +2具有“1—1驻点性”，给定x 1，x 2 R ，x 1＜x 2，设λ为实数，且λ≠，α=x 1+λx 21+λ，β=x 2+λx 11+λ，若|g (α)g (β)|＞|g (x 1)g (x 2)|，求λ的取值范围.江苏省盐城中学高二年级第二次随堂测验数 学 试 题（xx.12）（答案）一、填空题（本大题共14小题,每小题5分,计70分）1. 2．1 3. 4. 28_．5. 2)12()23()2()1(-=-++++++n n n n n6． _-4_． 7． 8． 9． -3. 10．．11.． 12． 13. 14． 6 个二、解答题（本大题共6小题，计90分. 请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．） 15.（文）已知.22:,0)6)(2(:,0m x m q x x p m +≤≤-≤-+> （1）若是的充分条件，求实数的取值范围； （2）若或为真命题，“且为假命题，求实数的取值范围. 解：(I)∵是的充分条件，∴[-2，6]是的子集 ∴ ∴实数的取值范围是 (Ⅱ)当时，. 据题意有,与一真一假.真假时,由假真时,由.76237362≤<-<≤-⇒⎩⎨⎧≤≤->-<x x x x x 或或∴实数的取值范围为15.（理）如图，在棱长为3的正方体中，. ⑴求两条异面直线与所成角的余弦值； ⑵求平面与平面所成的锐二面角的余弦值. （1）以为原点，建立空间直角坐标系， 如图所示,则,所以111111230cos ,,3310AC D E AC D E AC D E⋅<>===-⨯即两条异面直线与所成角的余弦值为(2) ()()()13,3,0,0,3,2,3,0,1.B BE D E =-=- 设平面的一个法向量为由得，所以，则不妨取 则16.已知在处都取得极值．（1）求、的值；（2）若对时，恒成立，求实数的取值范围．解：（1）在处都取得极值，即经检验符合（2）由（1）可知，由，得的单调增区间为，由，得的单调减区间为和，当时，，而所以，即在上的最小值为，要使对时，恒成立，必须17.张林在李明的农场附近建了一个小型工厂，由于工厂生产须占用农场的部分资源，因此李明每年向张林索赔以弥补经济损失并获得一定净收入．工厂在不赔付农场的情况下，工厂的年利润（元）与年产量（吨）满足函数关系．若工厂每生产一吨产品必须赔付农场元（以下称为赔付价格）．（1）将工厂的年利润（元）表示为年产量（吨）的函数，并求出工厂获得最大利润的年产量；（2）若农场每年受工厂生产影响的经济损失金额（元），在工厂按照获得最大利润的产量进行生产的前提下，农场要在索赔中获得最大净收入，应向张林的工厂要求赔付价格是多少？解：（Ⅰ）工厂的实际年利润为：()．ss t s st t w 221000)1000(2000+--=-=，当时，取得最大值．所以工厂取得最大年利润的年产量 (吨)． （Ⅱ）设农场净收入为元，则．将代入上式，得：． 又令，得． 当时，；当时，， 所以时，取得最大值．18.已知椭圆的左,右焦点分别为，其中也是抛物线的焦点，是与在第一象限的交点，且 （1）求椭圆的方程；（2）已知点是椭圆上一点，是椭圆上的两个动点，若直线的斜率与的斜率互为相反数，直线的斜率是否为定值？如果是，求出定值；反之，请说明理由. 解：（I ）设由抛物线定义， M 点C 1上，舍去.椭圆C 1的方程为 （II ）设直线的方程为代人椭圆方程得2223(34)4(32)4()1202k x k k x k ++-+--=设 ，可得 ，故5325322)8000(1000100081000s s s s v -=⨯+-='19.在平面直角坐标系中，已知椭圆的离心率为，且经过点，若分别是椭圆的右顶点和上顶点，直线与AB相交于点D，与椭圆相交于E、F两点.（1）求椭圆的方程；（2）若，求的值；（3）求四边形面积的最大值．19.解：（1），（2）直线的方程分别为，.如图，设，其中，且满足方程，故………①由知，得；由在上知，得．所以，化简得，解得或．（32h==又，所以四边形的面积为，当且仅当即当时，上式取等号．所以的最大值为．解法二：由题设，，．设，，由①得，，故四边形的面积为，当时，上式取等号．所以的最大值为．20.若函数在处的导数为，则称点称为函数的驻点，若点(1,1)为函数f(x)的驻点，则称f(x)具有“1—1驻点性”.（1）设函数f(x)=，其中.①求证：函数f(x)不具有“1—1驻点性”；②求函数f(x)的单调区间.（2）已知函数g(x)=bx3+3x2+cx+2具有“1—1驻点性”，给定x1，x2∈R，x1＜x2，设λ为实数，且λ≠，α=x1+λx21+λ，β=x2+λx11+λ，若|g(α)g(β)|＞|g(x1)g(x2)|，求λ的取值范围.解：（Ⅰ）①=-1+1x +ax∵=-1+1+a≠0， ∴函数f (x )不具有“1—1驻点性” ②由=-x+x+a x = -(x-12)2+a+14x(ⅰ)当a+14＜0,即a ＜-14时，＜0.∴f (x )是(0,+∞)上的减函数； (ⅱ)当a+14=0,即a =-14时，显然≤0.∴f (x )是(0,+∞)上的减函数； (ⅲ)当a+14＞0，即a ＞-14时，由=0得x=12±a+14 当-14＜a ＜0时，12-a+14＞0∴x ∈(0, a+12-a+14)时，＜0;x ∈( a+12-a+14, a+12+a+14)时，＞0; x ∈( a+12+a+14, +∞)时，＜0;综上所述：当a ≤-14时，函数f (x )的单调递减区间为(0,+∞)； 当-14＜a ＜0时，函数f (x )的单调递减区间为(0, a+12-a+14)和( a+12+a+14,+∞)，函数f (x )的单调递增区间为( a+12-a+14, a+12+a+14)；（Ⅱ）由题设得：=3bx 2+6x+c,∵g (x )具有“1—1驻点性”∴且即⎩⎨⎧b+3+c+2=13b+6+c=0解得⎩⎨⎧b=-1c=-3∴=-3x 2+6x-3=-3(x-1)2≤0，故g (x )在定义域R 上单调递减. ①当λ≥0时，α=x 1+λx 21+λ≥x 1+λx 11+λ=x 1，α=x 1+λx 21+λ＜x 2+λx 21+λ=x 2，即α∈[x 1,x 2),同理β∈(x 1,x 2] 11分 由g (x )的单调性可知：g (α)，g (β)∈[ g (x 2),g (x 1)]∴|g (α)-g (β)|≤|g (x 1)-g (x 2)|与题设|g (α)-g (β)|＞|g (x 1)-g (x 2)|不符.②当-1＜λ＜0时，α=x 1+λx 21+λ＜x 1+λx 11+λ=x 1，β=x 2+λx 11+λ＞x 2+λx 21+λ=x 2即α＜x 1＜x 2＜β∴g (β)＜g (x 2)＜g (x 1)＜g (α)∴|g (α)-g (β)|＞|g (x 1)-g (x 2)|，符合题设 ③当λ＜-1时，α=x 1+λx 21+λ＞x 2+λx 21+λ=x 2, β=x 2+λx 11+λ＜x 1+λx 11+λ=x 1，即β＜x 1＜x 2＜α ∴g (α)＜g (x 2)＜g (x 1)＜g (β)∴|g (α)-g (β)|＞|g (x 1)-g (x 2)|也符合题设由此，综合①②③得所求的λ的取值范围是λ＜0且λ≠-10eM36511 8E9F 躟23031 59F7 姷s30344 7688 皈27219 6A53 橓28558 6F8E 澎%40360 9DA8 鶨$M。

成都七中高 2024 届零诊模拟考试数学试题(理科)时间: 120 分钟 满分:150 分一、单选题：共12道小题，每题5分，共60分.1.设121iz i i-=++，则z 的虚部为 A.i B.3i C.1 D.32.直线1:10l x ay +-=与直线2:10l ax y ++=平行，则a= A.0 B.1 C.-1 D.1或-13.一组数据包括47、48、51、54、55，则这组数据的标准差为B.C.10 D.504.已知函数()f x 在其定义域R 上的导函数为()f x '，当x R ∈时，()0 f x '>是“()f x 单调递增”的 A.充要条件B.既不充分也不必要条件C.必要不充分条件D.充分不必要条件5.如图所示的算法框图思路源于我国古代数学名著《九章算术》中的“更相减相术”，执行该算法框图，若输入的a 、b 分别为36、96，则输出的a=（ ）A.0B.8C.12D.246.直线2x =与抛物线2:2(0)C y px p =>交于D 、E 两点，若0OD OE ⋅=，其中O 为坐标原点，则C 的准线方程为( )A.14x =-B.12x =-C.1x =-D.2x =-7.函数lg y x =的图象经过变换10:2x xy y ϕ''⎧=⎨=+⎩后得到函数()y f x ''=的图象，则()f x =A.1lg x -+B.1lg x +C.3lg x -+D.3lg x +8.有甲、乙、丙、丁四名学生参加歌唱比赛，其中只有一位获奖，有人走访了四人，甲说：“是乙或丙获奖.”乙说：“甲、丙都未获奖.”丙说：“我获奖了.”丁说：“是乙获奖.”四位歌手的话只有两句是对的，则获奖的歌手是 A.甲 B.乙 C.丙 D.丁9.设曲线C 的参数方程为1cos 1sin x y θθ=+⎧⎨=+⎩(θ为参数，且,22πθπ⎡⎤∈⎢⎥⎣⎦)，曲线C 上动点P 到直线:143x y l +=的最短距离为A.0B.15C.25D.110.关于圆周率π，数学史上出现过很多有创意的求法，如著名的浦丰实验和查理斯实验.受其启发，可通过设计如下实验来估计π值：先请100名同学每人随机写下一组正实数对(x ，y)，且要求x ，y 均小于1；再统计x 、y 和1作为三边长能形成钝角三角形的数对(x ，y)的个数m ；最后利用统计结果估计π值.假如某次实验结果得到m=28，那么本次实验可以将π值估计为 A.227 B.4715 C.7825 D.531711.点A 、B 在以PC 为直径的球O 的表面上，且AB BC ⊥，AB=BC=2，已知球O 的表面积是12π，设直线PB 和AC 所成角的大小为α，直线PB 和平面PAC 所成角的大小为β，四面体PABC 内切球半径为r ，下列说法中正确的个数是①BC ⊥平面PAB ；②平面PAC ⊥平面ABC ； ③sin cos αβ=：④12r > A.1 B.2 C.3 D.412.函数()1sin(11)x f x e x =--在[0,)+∞上的零点个数为A.1B.2C.3D.4二、填空题:共4道小题,每题5分，共20分.13.命题“0tan x x x ∀>>，”的否定为_____________.14.函数()cos xf x x=的图象在x π=处的切线方程为_____________.15.某区为了解全区12000名高二学生的体能素质情况，在全区高二学生中随机抽取了1000名学生进行体能测试，并将这1000名的体能测试成绩整理成如下频率分布直方图.根据此频率分布直方图，这1000名学生平均成绩的估计值为____________.16. 双曲线2222:1(,0)x y H a b a b -=>其左、右焦点分别为12,F F ，倾斜角为3π的直线2PF 与双曲线H 在第一象限交于点P ，设12F PF 内切圆半径为r ，若223PF r ≥∣，则双曲线H 的离心率的取值范围为______. 三、解答题：共5道大题，共70分.17.（12分）设函数321(1)()2(1)34f f x x x x f '-=-+-(1)求()1f '-、()1f 的值； (2)求()f x 在[0,2]上的最值.18.（12分)信创产业即信息技术应用创新产业，是一条规模庞大、体系完整的产业链，是数字经济的重要抓手之一.在政府、企业等多方面的共同努力下，中国信创产业市场规模不断扩大，市场释放出前所未有的活力.下表为2018—2022年中国信创产业规模（单位：千亿元），其中2018—2022年对应的代码依次为1~5.(1)从2018—2022年中国信创产业规模中任取2个数据，求这2个数据都大于10的概率.（2）由上表数据可知，可用指数型函数模型x y a b =⋅拟合y 与x 的关系，请建立关于x 的回归方程(a ，b 的值精确到0.01)，并预测2023年中国信创产业规模能否超过20千亿元. 参考数据:其中ln i i v y =,5115i i v v ==∑参考公式：对于一组数据()11,u w ，()22,u w ，…，(),n n u w ，其回归直线ˆˆˆwu αβ=+的斜率和截距的最小二乘估计公式分别为1221ˆni ii nii u w nwunu β=-=-=-∑∑，ˆˆw u αβ=- 19.（12分）如图，三棱柱111ABC A B C -中，侧面11ACC A 为矩形，AB AC ⊥且AB=AC=2,D 为11B C 的中点，1122AA B C ==. (1)证明:1//AC 平面1A BD ;（2）求平面1AB C 与平面1AA D 所成锐二面角的余弦值20.（12分）椭圆2222:1(0)x y C a b a b+=>>上顶点为B ，左焦点为F ，中心为0.已知T 为x 轴上动点，直线BT 与椭圆C 交于另一点D ；而P 为定点，坐标为(2,3)-，直线PT 与y 轴交于点Q.当T 与F 重合时，有||||PB PT =，且2BT BP BQ =+. (1)求椭圆C 的标准方程；(2)设T 的横坐标为t ，当(0,2)t ∈时，求DTQ 面积的最大值. 21.(12分）设函数()x f x e ax =-，其中a R ∈.(1)讨论函数()f x 在[1,)+∞上的极值；(2)若函数f(x)有两零点()1212,x x x x <，且满足1211x x λλ+>+，求正实数λ的取值范围. 22.（10分）在平面直角坐标系xOy 中，以O 为极点，x 轴的正半轴为极轴，建立极坐标系，曲线C和直线l 的极坐标方程分别为2sin 2cos a ρθθ=+和sin 4x πρ⎛⎫-= ⎪⎝⎭且二者交于M ，N 两个不同点.(1)写出曲线C 和直线l 的直角坐标方程；(2)若点P 的极坐标为(2,),||||PM PN π+=a 的值.理科数学参考答案13.00x ∃>，00tan x x ≤ 14.0x y += 15.80.516.5,24⎡⎫⎪⎢⎣⎭三、解答题：共5道大题，共70分. 17.解:(1)由题设知2(1)()22f f x x x ''-=-+,取1x =-，则有(1)(1)32f f ''--=+,即(1)6f '-=: 也即3213()2(1)32f x x x x f =-+-，取1x =，则有5(1)(1)6f f =-，即5(1)12f =故(1)6f '-=,5(1)12f =.(2)由(1)知32135()23212f x x x x =-+-,2()32(1)(2)f x x x x x '=-+=--,故max 5()(1)12f x f ==,min 5()(0)12f x f ==- 18.解：(1)从2018—2022年中国信创产业规模中任取2个数据有(8.1,9.6)，（8.1,11.5)，（8.1,13.8)，（8.1,16.7)，（9.6,11.5)，（9.6,13.8），(9.6,16.7），（11.5,13.8)，（11.5,16.7)，（13.8,16.7)，共10种情况，其中这2个数据都大于10的有(11.5,13.8)，（11.5,16.7)，(13.8,16.7)，共3种情况，所以2个数据都大于10的概率310P =(2)x y a b =⋅两边同时取自然对数得()ln ln ln ln x y a b a x b =⋅=+，则v lna xlnb =+. 因为5213, 2.45,55i i x v x ====∑,所以5152221538.5253 2.45ln 0.17755535i i i ii x v xvb xx =-=--⨯⨯===-⨯-∑∑ ·1 2.450.1773 1.919lna v x nb =-=-⨯=，所以 1.9190.177v x =+ 即ln 1.9190.177y x =+，所以 1.9190.177ˆe 6.81 1.19x x y+==⨯， 即y 关于x 的回归方程为ˆ 6.81 1.19x y=⨯. 2023年的年份代码为6，把x=6代入ˆ 6.81 1.19x y =⨯, 得66.81 1.19 6.81 2.8419.3420y =⨯=⨯≈<，所以预测2023年中国信创产业规模不会超过20千亿元. 19.公众号：高中试卷君解：（1）连接1AB 与A 、B 交于点O ，连接OD111ABC A B C -为三棱柱，11ABB A ∴为平行四边形，点O 为1AB 的中点 又D 为11B C 的中点，则1//AC OD ,又OD ⊂平面1A BD ,1AC ⊂/平面11,//A BD AC ∴平面1A BD . (2)CA AB ⊥，1CA AA ⊥,AB∩1AA A =，CA ∴⊥平面11ABB A1AB ⊂面11ABB A ，1CA AB ∴⊥ 222211(22)22AB CB AC ∴=-=-=AB=2，12AB =,122BB =，∴22211AB AB BB +=，即1AB AB ⊥以A 为坐标原点，AB ，1AB ，AC 分别为x 轴，y 轴，z 轴建立空间直角坐标系，A(0,0,0)，1(2,2,0)A -,B(2,0,0),1(0,2,0)B ,1(2,2,2)C -,D(-1,2,1)1(2,2,0)AA ∴=-,1(1,0,1)A D =1AB AB ⊥,AB AC ⊥,1AB AC A ⋂=AB ∴⊥平面1AB C ，则平面1AB C 的一个法向量为1(1,0,0)n =设平面1AA D 的法向量为2(,,)n x y z =，则121200AA n A D n ⎧⋅=⎪⎨⋅=⎪⎩，即2200x y x z -+=⎧⎨+=⎩令x=1,y=1,z=-1,∴2(1,1,1)n =-,设平面1AB C 与平面1AA D 所成二面角的大小为θ1212|1cos 31n n n n θ⋅⨯∴====∴平面1AB C 与平面1AA D20.解：(1)设F(-c,0)，由2BT BP BQ =+知2(-c ）=-2+0，即c=1， 由||||PB PT=知2222(20))[2(1)]0)b--+=---+，即b =则a=2，故椭圆C 的标准方程为22143x y +=(2)直线BT 的方程为x y =,与22143x y +=联立，可得()222243120t y y t +-+-=，且0>，有223124D t y t -=+，即D y =直线PT 的方程为2x y +=-,令x=0，可得Q y =由sin sin 3DTQ Q DDTQPTBPTBS y y y y QT DT DTQ QT DT SSSPT BT BTP PT BT ⋅-⋅⋅∠⋅====-⋅⋅∠⋅即2224DTQt t St -=+，(0,2)t ∈ 而22214t tt -≤+，当2t +=2t =时取等,且()0,2t ∈ 故DTQ 面积的最大值为221.解：(1)由()x f x e ax =-知()x f x e a '=-,1）当a e ≤时，且有[1,)x ∈+∞，()0f x '≥，()f x 单增，故无极值；2）当a e >时，有(1,ln )x a ∈，()0f x '<，()f x 单减，而(ln ,)x a ∈+∞，()0f x '>，()f x 单增，故()(ln )ln f x f a a a a ==-极小值，()f x 无极大值.综上，当a e ≤时，()f x 无极值；当a e >时，()f x 极小值为ln a a -，()f x 无极大值.（2）由（1）可知当a e >时，(ln )(1ln )0f a a a =-<，1(00f =>），且x f x →+∞→+∞，（）， 由零点存在定理可知120ln x a x <<<，而题设可知12120x x e ax e ax -=-=，消去a 可得221121x x x x x e e e x -==，令211x t x =>，且21ln t x x =-，即2ln 1t t x t =-,1ln 1t x t =-， 将其代入1211x x λλ+>+，整理可令得(1)(1)()ln 01t F t t t λλ+-=->+而()22221(1)1(1)()(1)(1)t t F t t t t t λλλλ'--+=-=++,1)当1λ≥时，且(1,)t ∈+∞，有22(1)()0(1)t F t t t λ'-≥>+，()F t 单增，F(t)>F(1)=0，满足题设； 2)当0<λ<1时，且211,t λ⎛⎫∈ ⎪⎝⎭，有()0F t '<，()F t 单减，F(t)<f(l)=0，不满足题设；综上，λ的取值范围为[1,)+∞.22.解：(1)由2sin 2cos a ρθθ=+，得22sin 2cos a ρρθρθ=+，故曲线C 的直角坐标方程为2222x y y ax +=+，即222()(1)1x a y a -+-=+;由sin 4πρθ⎛⎫-= ⎪⎝⎭sin cos 2ρθρθ-=故直线l 的直角坐标方程为2y x =+.（2）点P 的直角坐标为（-2,0），在直线l 上，而直线l的标准参数方程为2x y ⎧=-+⎪⎪⎨⎪=⎪⎩(t 为参数），将其代入2222x y y ax +=+，整理可得2)440t t a -++=. 由题设知222(3)4(44)2(1)0a a a ∆=+-+=->，解得1a ≠又12t t +=，1244t t a =+当a>-1,且a≠1时，有12,0t t >，则)12123PM PN t t t t a ++=+===+ 解得a=2;当1a ≤-时，有120t t ≤，则12121PM PN t t t t ++=-===- 得a=-4.故a 的值为2或-4..。

圆锥曲线复习一．定义 1.第一定义：椭圆：12122(2)MF MF a a F F +=>（当122a F F =时，轨迹是线段．．12F F ；当122a F F <时，轨迹不存在）双曲线：12122(2)MF MF a a F F -=<（当122a F F =时，轨迹是两条射线．．．．；当122a F F >时，轨迹不存在）2.圆锥曲线统一定义：平面上到定点（焦点）的距离与到定直线（相应准线）的距离之比为常数(0)e e >的动点的轨迹.01e <<时，轨迹是椭圆；1e =时，轨迹是抛物线；1e >时，轨迹是双曲线. 二．标准方程焦点在x 轴上的标准方程 焦点在y 轴上的标准方程椭圆 22221(0)x y a b a b +=>> 22221(0)y x a b a b +=>>双曲线 22221(,0)x y a b a b -=> 22221(,0)y x a b a b-=>抛物线 )0(22>=p px y （开口向右） 22(0)x py p =>（开口向上） 22(0)y px p =->（开口向左） 22(0)x py p =->（开口向下） 三．性质椭圆22221(0)x y a b a b +=>> 双曲线22221(,0)x y a b a b-=> 抛物线)0(22>=p px y1.基本量,,(),,ca b c a b c e aa b b p cca=+==2222222,,(),,c a b c a b c e aa b b p cca=+==2222222 2p p长轴长= ；短轴长= 实轴长= ；虚轴长=2.参数方程：22221(0)cos sin x y a b a b x a y b θθ+=>>=⎧⇔⎨=⎩ 22221(,0)sec tan x y a b a bx a y b θθ-=>=⎧⇔⎨=⎩222(0)22y px p x pt y pt =>⎧=⇔⎨=⎩ 范围 [][],,,x a a y b b ∈-∈- ,x a y R ≥∈ 0,x y R ≥∈ 对称性 轴：,x y 轴；中心：()0,0 轴：,x y 轴；中心：()0,0 轴：x 轴焦点 ()()12,0,0F c F c -、 ()()12,0,0F c F c -、 ,02p F ⎛⎫⎪⎝⎭顶点()()()()1212,0,,0,0,,0,A a A a B b B b -- ()()12,0,,0A a A a - ()0,0O准线方程 2a x c =± 2a x c=± 2p x =-渐近线方程 22220b x y y x a a b=±⇔-=焦半径1020;PF a ex PF a ex =+=-1020;PF a ex PF a ex =+=- 02pPF x =+焦点弦长12()2()AB a e x x =++左 12()2()AB a e x x =++左 12AB x x p =++焦点三角形周长4l a =；面积 2tan2ABC S b θ∆=焦点弦的性质 4,221221p x x p y y =-=4.其它性质：1. 椭圆：以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切双曲线：以焦点半径PF 1为直径的圆必与以实轴为直径的圆外切.2. 以焦点弦PQ 为直径的圆必与对应准线相离（椭圆）或相交（双曲线）或相切（抛物线）. 四．参数方程：例 题 讲 解8 求圆锥曲线方程19. 与椭圆221123x y +=有相同的焦点，且经过点)2,10(双曲线方程为_______；与双曲线116922=-y x 有共同的渐近线，且过点)32,3(-的双曲线方程为_______.20. 已知双曲线中心在原点且一个焦点为)0,7(F ,直线1-=x y 与其相交于M 、N 两点，MN 中点的横坐标为32-，则此双曲线的方程是 .21. 已知椭圆的中心在坐标原点O ，焦点在坐标轴上，直线y =x +1与椭圆交于P 和Q ，且,OP OQ PQ ⊥=.22.已知抛物线22(0)y px p =>，有一内接直角三角形，直角顶点在坐标原点，一直角边所在的直线方程为2y x =，斜边长等于.9 圆锥曲线的几何性质23. 抛物线方程为20(0)Ax By AB +=≠，则其焦点坐标为 .24.抛物线284y x =-的准线方程是 ，圆心在该抛物线的顶点，且与其准线相切的圆的方程是 .25.双曲线221916y x -=的渐近线方程是 ；焦点到准线的距离为 .26. 已知21,F F 为双曲线的左、右焦点，以双曲线右支上任一点P 为圆心，1PF 为半径的圆与以2F 为圆心，2121F F 为半径的圆内切，则双曲线两条渐近线的夹角是 .27. 设12F F ，分别是椭圆22221x y a b+=（0a b >>）的左、右焦点，若在其右准线上存在,P 使线段1PF 的中垂线过点2F ，则椭圆离心率的取值范围是 .28. 设双曲线22221(0)x y a b a b-=>>的半焦距为c 原点与直线1x y a b -=上点的距离的最小值为4，则双曲线的离心率为 .10 圆锥曲线定义的应用—求焦半径与焦点弦长29. 椭圆221259x y +=的焦点为12F F 、，点M 是椭圆上不与长轴端点重合的点，则12MF F ∆的周长 为 ；若M 到焦点1F 的距离为2,N 是1MF 的中点, 则ON = ；若M 到右准线的距离 为52，则M 到左焦点的距离为 ；30. 设F 为抛物线24y x =的焦点，A B C ，，为该抛物线上三点，若FA FB FC ++=0，则____FA FB FC ++=；过点F 的直线交抛物线于1122(,)(,)A x y B x y 、，若125y y +=，则AB = .31. 过抛物线24y x =的焦点的直线依次交抛物线和圆22(1)1x y -+=于点A B CD 、、、，则________AB CD ⋅=.11 圆锥曲线定义的应用—焦点弦三角形的运算32. 椭圆221259x y +=的焦点为12F F 、，点M 是椭圆上不与长轴端点重合的点，则满足12MF MF ⊥的点M 有 个；若12MF F ∆的面积为12_____PF PF ⋅=33.椭圆14922=+y x 的焦点为21,F F ，点P 为其上的动点，则12cos F PF ∠的最小值是 ．当21PF F ∠为钝角时，点P 横坐标的取值范围是_________.34. 若椭圆221(1)x y m m +=>与双曲线221(0)x y n n-=>有相同的焦点12F F P 、，是两曲线的一个 交点，则12F PF ∆的面积是 .35. 已知P 是以 1F ,2F 为焦点的椭圆)0,0(12222>>=+b a b y ax 上的一个点,若120PF PF ⋅=，且123tan 4PF F ∠=， 则此椭圆的离心率为 .12 解析几何最值问题36. 已知椭圆22143x y +=内有一点(1,1)M -，12,F F 是椭圆的左、右焦点，设P 是椭圆上的点，则2PM PF +的最大值为 ；若P 使212PM PF +最小，则P 点坐标为 .37. 已知实数,x y 满足：222220x y x y ++--=，则2x y +的最大值是 ; 13y x ++的取值范围是 ；点(0,1)与圆上点的距离的最小值是 .38. 已知实数,x y 满足：2233x y +=,则222x y xy +-的取值范围是 .13y x ++的取值范围是 ；点(),P x y 到直线240x y --=的距离的最小值为 .39.已知1,10,220x x y x y ≥⎧⎪-+≤⎨⎪--≤⎩则23x yz -=的最大值是 ；22(1)(1)x y ++-的最大值是 ；1y x+的取值范围是 .40. 在约束条件⎪⎪⎩⎪⎪⎨⎧≤+≤+≥≥4200x y s y x y x 下，当53≤≤s 时，目标函数y x z 23+=的最大值的变化范围是（ ）A. ]15,6[B. ]15,7[C. ]8,6[D. ]8,7[41. 是否存在同时满足下列条件的双曲线，若存在，求出其方程，若不存在，说明理由. (1)渐近线方程为2020x y x y +=-=及；（2）点(5,0)A 到双曲线上动点P42. 如图，已知椭圆122-+m y m x =1(2≤m ≤5),过其左焦点且斜率为1的直线与椭圆及其准线的交点从左到右的顺序为A 、B 、C 、D ，设f (m )=||AB |－|CD || (1)求f (m )的解析式； (2)求f (m )的最值13. 直线与圆锥曲线的位置关系43. 直线)(1R k kx y ∈+=与椭圆1522=+my x 恒有公共点，则m 的取值范围是 .44. 设双曲线22221(0)x y a b a b-=>，的右焦点为F ，右准线与一条渐近线交于A ，若FA 与双曲线的左右支都相交，则离心率e 的取值范围是 .45. 过点()01，与抛物线2(0)y mx m =>只有一个公共点的直线有 条.14弦长与中点问题弦长公式 设圆锥曲线:(,)0C f x y =与直线:l y kx b =+相交于1122(,),(,)A x y B x y 两点，则弦长AB 为： 1212AB x y =-=- 注：若弦AB 过圆锥曲线的焦点F ，则可用焦半径求弦长． 中点问题解法 1）点差法2）联立方程，用韦达定理求解.46. 已知双曲线22:12y C x -=，过点()3,0A 作直线l 与C 交于P Q 、两点，若PQ 的长等于双曲线C 的实轴长的4倍，求l 的倾斜角.47. 给定双曲线2222x y -=（1）过点(2,1)B 的直线l 与所给双曲线交于12P P 、两点，求线段12PP 中点的轨迹方程；（2）过点(1,1)B 能否作直线m ，使m 与所给双曲线交于两点12Q 、Q ，且点B 是线段12Q Q 的中点？若能，求出其方程，若不能，说明理由.48. 设()()1122,,A x y B x y 、两点在抛物线22y x =上，l 是AB 的垂直平分线. （1）当且仅当12x x +取何值时，直线l 经过抛物线的焦点F ，证明你的结论； （2）当直线l 的斜率为2时，求l 在y 轴上截距的取值范围.15 求值与求取值范围49. 直线l ：1+=kx y 与双曲线C ：1222=-y x 的右支交于不同的两点A 、B 。

第一章课后习题解答新课程标准数学选修2—2 导数及其应用第一章变化率与导数3．1）练习（P6附近，原3. 时，原油温度的瞬时变化率分别为和它说明在第3 h在第3 h和5 h的速率3 ℃／h油温度大约以1 ℃／h的速度下降；在第5 h 时，原油温度大约以上升.P8）练习（说. . 并且，函数在附近比在附近增加得慢函数在附近单调递增，在附近单调递增1的思想.明：体会“以直代曲”（P9）练习函数的图象为.根据图象，估算出，说明：如果没有信息技术，教师可以将此图直接提供给学生，然后让学生根据导数.的几何意义估算两点处的导数）（P10习题 A组、在处，虽然，然而1.. 所以，企业甲比企业乙治理的效率高.说明：平均变化率的应用，体会平均变化率的内涵.、，所以，2的速度下降.附近以这说明运动员在s m／s的瞬时速度就是函数在时的导数.3、物体在第5 s，所以，.J.10 m／s，它在第5 s的动能因此，物体在第5 s时的瞬时速度为.4、设车轮转动的角度为，时间为，则由题意可知，当时，. 所以，于是.车轮转动开始后第 s时的瞬时角速度就是函数在时的导数.，所以.因此，车轮在开始转动后第 s时的瞬时角速度为.2,3,4.题是对了解导数定义及熟悉其符号表示的巩固说明：第同理可得，. 5、由图可知，函数在处切线的斜率大于零，所以函数在附近单调递增说. 单调递减，单调递减，0，附近分别单调递增，2几乎没有变化，函数在，.明：“以直代曲”思想的应用、第一个函数的图象是一条直线，其斜率是一个小于零的常数，因此，其导数的图6）所示；第二个函数的导数恒大于零，并且随着的增加，的值也在增加；象如图（1对于第三个函数，当小于零时，小于零，当大于零时，大于零，并且随着的增加，的值也在增加. 以下给出了满足上述条件的导函数图象中的一种.说明：本题意在让学生将导数与曲线的切线斜率相联系.习题 B组（P11）1、高度关于时间的导数刻画的是运动变化的快慢，即速度；速度关于时间的导数刻.画的是速度变化的快慢，根据物理知识，这个量就是加速度．、2这个过程. 说明：由给出的的信息获得的相关信息，并据此画出的图象的大致形状基于对导数内涵的了解，以及数与形之间的相互转换.）的题意可知，函数的图象在点处的切线斜率为，所以此点附近曲线呈下、由（13）（3同理可得（2）降趋势. 首先画出切线的图象，然后再画出此点附近函数的图象..下面是一种参考答案某点处函数图象的大致形状.说明：这是一个综合性问题，包含了对导数内涵、导数几何意义的了解，以及对以直代曲思想的领悟. 本题的答案不唯一.1．2导数的计算练习（P18）1、，所以，，.2、（1）；（2）；（3）；（4）；（5）；（6）.习题 A组（P18）1、，所以，.2、.3、.4、（1）；（2）；（3）；（4）；（5）；（6）.5、. 由有，解得.6、（1）；（2）.7、.8、（1）氨气的散发速度.（2），它表示氨气在第7天左右时，以克／天的速率减少.习题 B组（P19）1、（1）（2）当越来越小时，就越来越逼近函数.（3）的导数为.2、当时，. 所以函数图象与轴交于点.，所以.所以，曲线在点处的切线的方程为.2、. 所以，上午6:00时潮水的速度为m／h；上午9:00时潮水的速度为m／h；中午12:00时潮水的速度为m／h；下午6:00时潮水的速度为m／h.1．3导数在研究函数中的应用）P26（练习．）因为，所以.、（11当，即时，函数单调递增；. 当，即时，函数单调递减.（2）因为，所以当，即时，函数单调递增；. 当，即时，函数单调递减.（3）因为，所以当，即时，函数单调递增；. 当，即或时，函数单调递减.4）因为，所以（当，即或时，函数单调递增；. 当，即时，函数单调递减、2.3、因为，所以）当时，（1 .注：图象形状不唯一，即时，函数单调递增；，即时，函数单调递减.2）当时，（，即时，函数单调递增；，即时，函数单调递减.、证明：因为，所以.4当时，，因此函数在内是减函数.P29）练习（1、是函数的极值点，.其中是函数的极大值点，是函数的极小值点.（1）因为，所以2、. 令，得.当时，，单调递增；当时，，单调递减. 所以，当时，有极小值，并且极小值为.2）因为，所以（. 令，得下面分两种情况讨论：①当，即或时；②当，即时.当变化时，，变化情况如下表：3＋－00＋单调递增54单调递增单调递减54因此，当时，有极大值，并且极大值为；.当时，有极小值，并且极小值为3 （）因为，所以.令，得.下面分两种情况讨论：.①当，即时；②当，即或时．当变化时，，变化情况如下表：2－0－0＋单调递减22单调递增单调递减因此，当时，有极小值，并且极小值为；22当时，有极大值，并且极大值为. （4）因为，所以. 令，得下面分两种情况讨论：①当，即时；②当，即或时.当变化时，，变化情况如下表：1－0＋0－单调递减单调递减单调递增2因此，当时，有极小值，并且极小值为；当时，有极大值，并且极大值为2）P31练习（1（）在上，当时，有极小值，并且极小值为.又由于，..因此，函数在上的最大值是20、最小值是）在上，当时，有极大值，并且极大值为；（2当时，有极小值，并且极小值为；又由于，.. 因此，函数在上的最大值是54、最小值是（3.）在上，当时，有极大值，并且极大值为又由于， ..因此，函数在上的最大值是 22、最小值是（4）在上，函数无极值.. 因为，因此，函数在上的最大值是、最小值是.组习题 A（P31）1（）因为，所以.1、因此，函数是单调递减函数.（2）因为，.，所以，因此，函数在上是单调递增函数 .）因为，所以（ 3.因此，函数是单调递减函数 .（ 4.）因为，所以.因此，函数是单调递增函数21（）因为，所以.、当，即时，函数单调递增.当，即时，函数单调递减. .）因为，所以2（.当，即时，函数单调递增当，即时，函数单调递减.（3）因为，所以.因此，函数是单调递增函数.（4）因为，所以.当，即或时，函数单调递增.当，即时，函数单调递减.3、（1）图略. （2）加速度等于0.4、（1）在处，导函数有极大值；（2）在和处，导函数有极小值；（3）在处，函数有极大值；（4）在处，函数有极小值.5、（1）因为，所以.令，得.当时，，单调递增；当时，，单调递减.所以，时，有极小值，并且极小值为.（2）因为，所以.令，得.下面分两种情况讨论：①当，即或时；②当，即时.当变化时，，变化情况如下表：2＋－0＋0单调递增单调递减单调递增161因此，当时，有极大值，并且极大值；当时，有极小值，并且极小值为.（.3）因为，所以. 令，得下面分两种情况讨论：①当，即或时；②当，即时.当变化时，，变化情况如下表：2＋00－＋单调递增单调递增22单调递减22；因此，当时，有极大值，并且极大值为.当时，有极小值，并且极小值为（4）因为，所以.令，得.下面分两种情况讨论：①当，即或时；②当，即时.，变化情况如下表：当变化时，4－0＋0－单调递减128单调递增单调递减因此，当时，有极小值，并且极小值为；当时，有极大值，并且极大值为128.）在上，当时，函数有极小值，并且极小值为.6、（1由于，，. 所以，函数在上的最大值和最小值分别为9，；（2）在上，当时，函数有极大值，并且极大值为16.当时，函数有极小值，并且极小值为，由于，. 所以，函数在上的最大值和最小值分别为16，. （3）在上，函数在上无极值由于，，所以，函数在上的最大值和最小值分别为，.（4）当时，有极大值，并且极大值为128..由于，，所以，函数在上的最大值和最小值分别为128，. 组（P32）习题 B.1）证明：设，1、（因为，所以在内单调递减因此，，即，. 图略2）证明：设，.（因为，所以，当时，，单调递增，；当时，，单调递减，；，. 图略又. 因此，）证明：设，.（3因为，所以，当时，，单调递增，；，单调递减，当时，；. 图略综上，，.（4）证明：设，因为，，单调递增，所以，当时，；当时，，单调递减，；.. 当时，显然因此，，）可知，. 由（3. 综上，，图略若有极值，则. ）函数的图象大致是个“双峰”图象，类似“”或“”的形状1（、2．在整个定义域上有且仅有一个极大值和一个极小值，从图象上能大致估计它的单调区间.（2）因为，所以.下面分类讨论：当时，分和两种情形：①当，且时，设方程的两根分别为，且，当，即或时，函数单调递增；当，即时，函数单调递减.当，且时，此时，函数单调递增.②当，且时，设方程的两根分别为，且，当，即时，函数单调递增；当，即或时，函数单调递减.当，且时，此时，函数单调递减1．4生活中的优化问题举例习题 A组（P37）1、设两段铁丝的长度分别为，，则这两个正方形的边长分别为，，两个正方形的面积和为，.令，即，.当时，；当时，.因此，是函数的极小值点，也是最小值点.所以，当两段铁丝的长度分别是时，两个正方形的面积和最小.2、如图所示，由于在边长为的正方形铁片的四角截去四个边长为的小正方形，做成一个无盖方盒，所以无盖方盒的底面为正方形，且边长为，高为.（1）无盖方盒的容积，.（2）因为，所以.令，得（舍去），或.当时，；当时，.因此，是函数的极大值点，也是最大值点.所以，当时，无盖方盒的容积最大.3、如图，设圆柱的高为，底半径为，（第2题）则表面积由，得.因此，，.令，解得.当时，；当时，.因此，是函数的极小值点，也是最小值点. 此时，..所以，当罐高与底面直径相等时，所用材料最省.4、证明：由于，所以令，得，. 可以得到，是函数的极小值点，也是最小值点这个结果说明，用个数据的平均值表示这个物体的长度是合理的，. 这就是最小二乘法的基本原理，半圆的面积为，，则半圆的半径为m5、设矩形的底宽为m m矩形的面积为，矩形的另一边长为因此铁丝的长为，.令，得（负值舍去）.当时，；当时，.因此，是函数的极小值点，也是最小值点.m时，所用材料最省所以，当底宽为、利润等于收入减去成本，而收入等于产量乘单价.6由此可得出利润与产量的函数关系式，再用导数求最大利润.收入，利润，.求导得令，即，.；；当时，当时，因此，.是函数的极大值点，也是最大值点,所以，产量为84时，利润最大）组（P37习题 B、设每个房间每天的定价为元，1.那么宾馆利润，. 令，解得.当时，；当时，因此，是函数的极大值点，也是最大值点 .元时，宾馆利润最大. 所以，当每个房间每天的定价为3502、设销售价为元／件时，利润，..令，解得. 当时，；当时，. 当是函数的极大值点，也是最大值点. 所以，销售价为元／件时，可获得最大利润5定积分的概念1．P42）练习（.说明：进一步熟悉求曲边梯形面积的方法和步骤，体会“以直代曲”和“逼近”的思想.练习（P45）1、，.于是取极值，得说明：进一步体会“以不变代变”和“逼近”的思想.2、km.说明：进一步体会“以不变代变”和“逼近”的思想，熟悉求变速直线运动物体路.程的方法和步骤（练习P48）. 说明：进一步熟悉定积分的定义和几何意义.从几何上看，表示由曲线与直线，，所围成的曲边梯形的面积. A组（P50）习题（1）；1、（2；）（3）.说明：体会通过分割、近似替换、求和得到定积分的近似值的方法.（m）；2、距离的不足近似值为：m）. 距离的过剩近似值为：（. 用分点 3、证明：令将区间等分成个小区间，在每个小区间上任取一点作和式，从而，说明：进一步熟悉定积分的概念.，以及曲线所围成的曲边梯形的面积，即4、根据定积分的几何意义，表示由直线，四分之一单位圆的面积，因此.）.5、（1和曲线所围成的曲边梯形的面积的相反数.由于在区间上，所以定积分表示由直线，，. （2）根据定积分的性质，得由于在区间上，在区间上，所以定积分等于位于轴上方的曲边梯形面积减去位于轴.下方的曲边梯形面积3）根据定积分的性质，得（由于在区间上，在区间上，所以定积分等于位于轴上方的曲边梯形面积减去位于轴.下方的曲边梯形面积）中，由于在区间上是非正的，在区间上是非负的，如果直接利用定义3说明：在（把区间分成等份来求这个定积分，那么和式中既有正项又有负项，而且无法抵挡一可以将定积分化为，这样，在区间和区间上的3. 利用性质些项，求和会非常麻烦由此可进而得到定积分的值. 再利用定积分的定义，符号都是不变的，容易求出，，见，利用定积分的性质可以化简运算.）中，被积函数在积分区间上的函数值有正有负，通过练习进一步体会定32）（在（.积分的几何意义P50）组 B（习题1、该物体在到（单位：s）之间走过的路程大约为145 m.说明：根据定积分的几何意义，通过估算曲边梯形内包含单位正方形的个数来估计．物体走过的路程.）.2、（1）；2）过剩近似值：（m （）不足近似值：（m. （m）（3）；）分割3、（1在区间上等间隔地插入个分点，将它分成个小区间：，，，……，，其长度为记第个区间为（）.，……，上质量分别记作：把细棒在小段，，. 则细棒的质量）近似代替（2当很大，即很小时，在小区间上，可以认为线密度的值变化很小，近似地等于是，细棒在小段上质. 于一个常数，不妨认为它近似地等于任意一点处的函数值.量（））求和（3得细棒的质量 .（4）取极限，所以.. 细棒的质量．6微积分基本定理1（P55）练习24；；（4）（50； 2）；（3）（1））.0；（8 （6）；（7）（5）；说明：本题利用微积分基本定理和定积分的性质计算定积分.P55）习题 A组（（3）；）；（2）；1、（1 （4）；（5）；（6）.说明：本题利用微积分基本定理和定积分的性质计算定积分.2、.它表示位于轴上方的两个曲边梯形的面积与轴下方的曲边梯形的面积之差. 或表述为：位于轴上方的两个曲边梯形的面积（取正值）与轴下方的曲边梯形的面积（取负值）的代数和.习题 B组（P55）1、（1）原式＝；（2）原式＝；（3）原式＝.2、（1）；（2）；（3）；（4）.3、（1）.（2）由题意得 ..这是一个超越方程，为了解这个方程，我们首先估计的取值范围，根据指数函数的性质，当时，，从而因此，.因此，，. 所以，. 从而，在解方程时，可以忽略不计）.，解之得（s 因此，.组中的习题涉及到被积函数是简单的复合函数的定积分，可视学生的具体说明：B情况选做，不要求掌握.7定积分的简单应用1．P58）练习（（1）；（2）1.说明：进一步熟悉应用定积分求平面图形的面积的方法与求解过程.P59）练习（）. 、（m1.J、（）2）组（P60习题 A.（2）（1）2； 1、.2、.4s 时物体达到最大高度. 3、令，即. 解得即第.m）最大高度为（，后两物体相遇，则 4、设s.5s后相遇解之得. 即两物体）.（此时，物体离出发地的距离为 m解之得.5、由，得.）.所做的功为（J后完全停止.. 因此，火车经过10s6、（1）令，解之得.（m）2 （））组（P60习题 B）表示圆与轴所围成的上、（11半圆的面积，因此）表示圆与直线（2所围成的图形（如图所示）的面积，. 因此，2、证明：建立如图所示的平面直角坐标系，可设抛物线的方程为，则，所以.从而抛物线的方程为 .于是，抛物线拱的面积.（第题））21（.3、如图所示解方程组得曲线与曲线交点的横坐标，..于是，所求的面积为、证明：4.题）2（第复习参考题第一章P65A组（）.）2（；3）1（、1．）；（22、（1）；）. （4（3）；、.3.）. 因为红茶的温度在下降4、（1 （2）表明在3℃附近时，红茶温度约以4℃／min的速度下降. 图略.5、因为，所以.当，即时，单调递增；当，即时，单调递减.6、因为，所以.当，即时，有最小值.由，得. 又因为，所以.7、因为，所以.当，即，或时，函数可能有极值.由题意当时，函数有极大值，所以.由于＋－0＋0单调递增单调递减极小值单调递增极大值.. 此时，，所以，当时，函数有极大值.8、设当点的坐标为时，的面积最小，因为直线过点，. 所以直线的方程为，即.当时，，即点的坐标是. 因此，的面积令，即 .，不合题意舍去. 当，或时，由于2＋0－单调递增极小值单调递减所以，当，即直线的倾斜角为时，的面积最小，最小面积为2.、.9.m. 因为钢条长为m10、设底面一边的长为，另一边的长为所以，长方体容器的高为.设容器的容积为，则，.. 令，即，或. 所以，（舍去）；当时，. 当时，因此，是函数在的极大值点，也是最大值点.3 m.所以，当长方体容器的高为1 m时，容器最大，最大容器为11、设旅游团人数为时，旅行社费用为.令，即，.，. 又，. 所以，是函数的最大值点.所以，当旅游团人数为150时，可使旅行社收费最多.、设打印纸的长为cm时，可使其打印面积最大12因为打印纸的面积为，长为，所以宽为，打印面积. ，.令，即，（负值舍去），. 是函数在内唯一极值点，且为极大值，从而是最大值点. 所以，打印纸的长、宽分别约为，时，可使其打印面积最大.13、设每年养头猪时，总利润为元 . 则. 令，即，.当时，；当时，. 是函数在内唯一极值点，且为极大值点，从而是最大值点元.头猪时，可使总利润最大，最大总利润为所以，每年养300250001；（3））；（2）；114、（4）原式＝；（）原式＝. （515、略. 说明：利用函数图象的对称性、定积分的几何意义进行解释.16、.17、由，得. 解之得.所做的功为（J）第一章复习参考题B组（P66）1、（1）. 所以，细菌在与时的瞬时速度分别为0和.（2）当时，，所以细菌在增加；当时，，所以细菌在减少.2、设扇形的半径为，中心角为弧度时，扇形的面积为.因为，，所以.，.令，即，，此时为2弧度.是函数在内唯一极值点，且是极大值点，从而是最大值点.所以，扇形的半径为、中心角为2弧度时，扇形的面积最大.3、设圆锥的底面半径为，高为，体积为，那么.因此，，..令，解得容易知道，是函数的极大值点，也是最大值点.所以，当时，容积最大.把代入，得.由，得.所以，圆心角为时，容积最大.4、由于，所以.设船速为km／h时，总费用为，则，令，即，.容易知道，是函数的极小值点，也是最小值点.当时，（元／时）所以，船速约为24km／h时，总费用最少，此时每小时费用约为941元.5、设汽车以km／h行驶时，行车的总费用，令，解得（km／h）. 此时，（元）容易得到，是函数的极小值点，也是最小值点.因此，当时，行车总费用最少.所以，最经济的车速约为53km／h；如果不考虑其他费用，这次行车的总费用约是114元.6、原式＝.7、解方程组得，直线与抛物线交点的横坐标为，.抛物线与轴所围图形的面积.由题设得.又因为，所以. 于是.说明：本题也可以由面积相等直接得到，由此求出的值. 但计算较为烦琐.新课程标准数学选修2—2第二章课后习题解答第二章推理与证明2．1合情推理与演绎推理练习（P77）1、由，猜想.2、相邻两行数之间的关系是：每一行首尾的数都是1，其他的数都等于上一行中与之相邻的两个数的和.3、设和分别是四面体和的体积，则.练习（P81）.、略1．2、因为通项公式为的数列，……………………大前提若，其中是非零常数，则是等比数列；……………………………小前提又因为，则，则；……………………结论所以，通项公式为的数列是等比数列.因为这个推理的大前提是“在同一个三角形中，大边. 3、由，得到的推理是错误的.对大角”，小前提是“”，而与不在同一个三角形中）组（P83习题 A. 1、.2、.、当时，；当时，；当时，3.、（，且）4.、（，且）5 .6、如图，作∥交于因为两组对边分别平行的四边形是平行四边形，. 又因为∥，∥. 所以四边形是平行四边形 . 因为平行四边形的对边相等又因为四边形是平行四边形.所以.因为与同一条线段等长的两条线段的长度相等，6题）（第 , 所以又因为，因为等腰三角形的两底角是相等的., 所以又因为△是等腰三角形因为平行线的同位角相等所以又因为与是平行线和的同位角,因为等于同角的两个角是相等的，所以又因为，,）（P84组习题 B.，，猜想1、由，，，、略. 3.2、略直接证明与间接证明 2．2 P89）练习（、因为，所以，命题得证.1、要证，只需证，2即证，即证，.只需要，即证，这是显然成立的. 所以，命题得证，、因为 3又因为，从而，所以，命题成立.说明：进一步熟悉运用综合法、分析法证明数学命题的思考过程与特点.练习（P91）1、假设不是锐角，则. 因此.. °矛盾180这与三角形的内角和等于. 从而，一定是锐角.所以，假设不成立、假设，，成等差数列，则.2所以，化简得，从而，即，. 所以，假设不成立. 这是不可能的.从而，，，不可能成等差数列.说明：进一步熟悉运用反证法证明数学命题的思考过程与特点）（P91习题 A组.1、由于，因此方程至少有一个跟假设方程不止一个根，则至少有两个根，不妨设是它的两个不同的根，①则②①－②得因为，所以，从而，这与已知条件矛盾，故假设不成立 .、因为 2. ①展开得，即假设，则，即所以.因为，都是锐角，所以，从而，与已知矛盾.因此..，即①式变形得又因为，所以.说明：本题也可以把综合法和分析法综合使用完成证明.3、因为，所以，从而.另一方面，要证，只要证即证，即证由可得，，于是命题得证.说明：本题可以单独使用综合法或分析法进行证明，但把综合法和分析法结合使用进行证明的思路更清晰.4、因为的倒数成等差数列，所以.假设不成立，即，则是的最大内角，所以（在三角形中，大角对大边），从而 . 这与矛盾.所以，假设不成立，因此，.习题 B组（P91）1、要证，由于，所以只需要，即证.因为，所以只需要，即证.由于为一个三角形的三条边，所以上式成立. 于是原命题成立.2、由已知条件得①，②要证，只要证，只要证，由①②，得．，.所以，，于是命题得证 3、由……①，即. 得要证即证即证. 化简得，这就是①式. 所以，命题成立说明：用综合法和分析法证明命题时，经常需要把两者结合起来使用.2．3数学归纳法练习（P95）1、先证明：首项是，公差是的等差数列的通项公式是.（1）当时，左边＝，右边＝，因此，左边＝右边. 所以，当时命题成立.（2）假设当时，命题成立，即.那么，.所以，当时，命题也成立.根据（1）和（2），可知命题对任何都成立.再证明：该数列的前项和的公式是.（1）当时，左边＝，右边＝，因此，左边＝右边. 所以，当时命题成立.（2）假设当时，命题成立，即.那么，所以，当时，命题也成立.根据（1）和（2），可知命题对任何都成立.2、略.习题 A组（P96）1、（1）略.（2）证明：①当时，左边＝1，右边＝，因此，左边＝右边. 所以，当时，等式成立.②假设当时等式成立，即.那么，.所以，当时，等式也成立.根据①和②，可知等式对任何都成立.（3）略.2、，，.由此猜想：.下面我们用数学归纳法证明这个猜想.）当时，左边＝，右边＝，1（因此，左边＝右边. 所以，当时，猜想成立.（2）假设当时，猜想成立，即.那么，.所以，当时，猜想也成立.根据（1）和（2），可知猜想对任何都成立.习题 B组（P96）1、略2、证明：（1）当时，左边＝，右边＝，因此，左边＝右边. 所以，当时，等式成立.（2）假设当时，等式成立，即.那么，.所以，当时，等式也成立.根据（1）和（2），可知等式对任何都成立.第二章复习参考题A组（P98）1、图略，共有（）个圆圈.2、（）.3、因为，所以，，……猜想.4、运算的结果总等于1.5、如图，设是四面体内任意一点，连结，，，并延长交对面于，，，，则用“体积法”证明：、要证 6只需证即证①由，得.所以，命题得证. .又因为，所以，变形即得①式1）当时，左边＝，右边＝，7、证明：（.因此，左边＝右边. 所以，当时，等式成立2（）假设当时，等式成立，（第题）5.即. 那么，所以，当时，等式也成立.根据（1）和（2），可知等式对任何都成立.第二章复习参考题B组（P47）1、（1）25条线段，16部分；（2）条线段；（3）最多将圆分割成部分.下面用数学归纳法证明这个结论.①当时，结论成立.②假设当时，结论成立，即：条线段，两两相交，最多将圆分割成部分当时，其中的条线段两两相交，最多将圆分割成部分，第条线段与线段都相交，最多增加个部分，因此，条线段，两两相交，最多将圆分割成部分所以，当时，结论也成立.根据①和②，可知结论对任何都成立.2、要证因为只需证由已知条件，得，，代入上式的左端，得因此，新课程标准数学选修2—2第三章课后习题解答第三章数系的扩充与复数的引入3．1数系的扩充和复数的概念练习（P104）1、实部分别是，，，0，0，0；虚部分别是，1，0，，1，0.2、，，0，是实数；，，，，，是虚数；，，是纯虚数..、由，得3．练习（P105）1、：，：，：，：，：，：，：，：.2、略.3、略.习题 A组（P106）1、（1）由，得.（2）由，得2、（1）当，即或时，所给复数是实数.（2）当，即或时，所给复数是虚数.（3）当，即时，所给复数是纯虚数.3、（1）存在，例如，，等等.（2）存在，例如，，等等.（3）存在，只能是.4、（1）点在第一象限. （2）点在第二象限.（3）点位于原点或虚轴的下半轴上. （4）点位于实轴下方.5、（1）当，即或时，复数对应的点位于第四象限.（2）当，或，即或或时，复数对应的点位于第一、三象限.（3）当，即时，复数对应的点位于直线上.6、（1）；（2）.习题 B组（P55）1、复数对应的点位于如图所示的图形上.2、由已知，设（）.则解得所以3、因为，所以，，，，这4个点都在以原点为圆心，半径为的圆上.3．2复数代数形式的四则运算练习（P109）1、（1）5；（2）；（3）；（4）0.2、略.练习（P111）1、（1）；（2）；（3）；2、（1）；（2）；（3）5.3、（1）；（2）；（3）；（4）.习题 A组（P112）1、（1）；（2）；（3）；（4）.。

零诊复习资料（仅供7班使用） 第2讲 函数的性质【知识梳理】 一、单调性1.定义：设D 是函数()f x 定义域的子区间，对任意12,x x D ∈，当12x x <时：(1) 都有()()12f x f x <⇔()f x 在区间D 上是增函数； (2) 都有()()12f x f x >⇔()f x 在区间D 上是减函数.2.判定：(1) 定义法；(2) 图象法：(3) 结论法(所学初等函数的单调性) ；(4) 复合函数的单调性：同增异减，小心范围.3. 用定义证单调性的步骤：任取——作差——变形——定号——结论. 二、奇偶性1.定义：对函数()f x 定义域内的任意x ： (1)都有()()f x f x -=-⇔()f x 为奇函数； (2)都有()()f x f x -=⇔()f x 为偶函数.点拨：奇、偶函数的定义域关于原点对称.2.性质：(1) 奇函数()f x ⇔图象关于原点对称；若()0f 有意义，则()00f =；（2）偶函数()f x ⇔图象关于y 轴对称()()f x f x ⇔=；(3) 在关于原点对称的两个区间上：奇函数同单调；偶函数异单调. 3.用定义判奇偶性的步骤：求定义域——定()f x -与()f x 的关系——下结论.三、对称性:轴对称,中心对称.对函数()f x 的定义域内的任何一个自变量x ：1.若都有()()f a x f a x -=+，则()f x 的图象关于直线x a =对称；若都有()()f a x f b x -=+，则()f x 的图象关于直线2a bx +=对称。

2.若都有()()f a x f a x -=-+，则()f x 的图象关于点(),0a 对称；若都有()()f a x f b x -=-+，则()f x 的图象关于点,02a b +⎛⎫⎪⎝⎭对称。

若都有()()22f x f a x b +-=,则()y f x =的图象关于点(),a b 对称.四、周期性1. 定义：如果存在非零常数T ，对函数()f x 定义域内任意的x ，都有()()f x T f x +=，则称函数()f x 是周期函数，T 是它的一个周期.2.性质：(1) 若T 是()f x 的一个周期, 则(),0kT k Z k ∈≠也是()f x 的周期；(2) 若T 是()f x 的一个周期，则()f x ω ()0ω≠是周期函数，且一个周期是||ωT .3. 结论：(1)若()y f x =图象有两条对称轴,()x a x b a b ==≠，则()y f x =必是周期函数，且一周期为2||T a b =-；(2)若()y f x =图象有两个对称中心(,0),(,0)()A a B b a b ≠，则()y f x =是周期函数，且一周期为2||T a b =-；(3)如果函数()y f x =的图象有一个对称中心(,0)A a 和一条对称轴()x b a b =≠，则函数()y f x =必是周期函数，且一周期为4||T a b =-； (4)若函数()f x 满足下列条件之一, 则()f x 是周期函数,且一个周期为2T a =()0a ≠：①()()f a x f x +=-；②1()()f x a f x +=；③1()()f x a f x +=-.例2．(1) 若定义在R 上的奇函数()f x 以T 为周期，则函数()f x 在区间[,]T T -上至少有 5 个零点.(2)函数()f x 的定义域为R ，若()1f x +和()1f x -都是奇函数，则函数()()g x f x =，{}1,1,3,5x ∈-的值域是 {}0.(3)定义在R 上的偶函数()f x 满足(2)()f x f x +=-，且在[6,4]--上是增函数，在锐角ABC ∆中，令(sin sin )m f A B =+，(cos cos )n f A C =+，则m 和n 的大小关系为_______ m n <. (4)函数()12s i n 1f x x x π=+-在区间[]2,4-上的所有零点之和等于 8 .(5) 设()f x 是连续的偶函数，且在()0,+∞是单调函数，则方程()34x f x f x +⎛⎫= ⎪+⎝⎭所有根之和为 8-.第3讲 初等函数【知识梳理】1．指数与对数的运算性质： （1）指数式与对数式的互化：log (0,1,0)b a a N b N a a N =⇔=>≠>。