11.2.5 直角三角形全等判定(HL) 修订版教案-

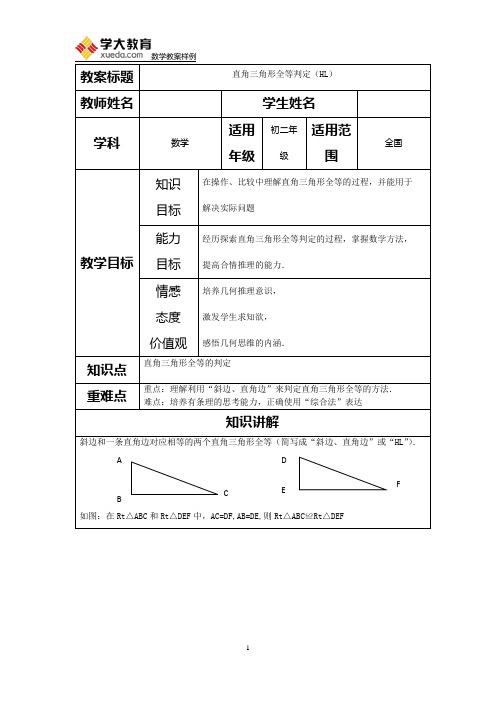
教案标题 直角三角形全等判定（HL ）教师姓名 学生姓名学科数学适用年级初二年级适用范围全国教学目标知识 目标 在操作、比较中理解直角三角形全等的过程，并能用于 解决实际问题能力目标 经历探索直角三角形全等判定的过程，掌握数学方法， 提高合情推理的能力． 情感 态度 价值观培养几何推理意识， 激发学生求知欲， 感悟几何思维的内涵．知识点 直角三角形全等的判定重难点重点：理解利用“斜边、直角边”来判定直角三角形全等的方法． 难点：培养有条理的思考能力，正确使用“综合法”表达知识讲解斜边和一条直角边对应相等的两个直角三角形全等（简写成“斜边、直角边”或“HL ”）．如图：在Rt △ABC 和Rt △DEF 中，AC=DF,AB=DE,则Rt △ABC ≌Rt △DEFA BCDEF例题讲解例1. AC ⊥BC ，BD ⊥AD ，AC=BD ，求证BC=AD ．[答案]BC=AD ． [详细答案】【思路点拨】欲证BC=•AD ，•首先应寻找和这两条线段有关的三角形，•这里有△ABD 和△BAC ，△ADO 和△BCO ，O 为DB 、AC 的交点，经过条件的分析，△ABD 和△BAC•具备全等的条件． 证明：∵AC ⊥BC ，BD ⊥BD ， ∴∠C 与∠D 都是直角．在Rt △ABC 和Rt △BAD 中，,,AB BA AC BD =⎧⎨=⎩ ∴Rt △ABC ≌Rt △BAD （HL ）． ∴BC=AD ．例2.下列说法正确的是（ ）A.面积相等的两个直角三角形全等B.周长相等的两个直角三角形全等C.斜边相等的两个直角三角形全等D.有一个锐角和斜边上的高对应相等的两个直角三角形全等 [答案] D[详细答案]周长和面积相等的两个三角形全等是错误的，斜边相等的两个三角形全等不具备全等的条件，只有D 答案具备全等的条件。

例3.有两个长度相同的滑梯，左边滑梯的高度AC•与右边滑梯水平方面的长度DF 相等，两个滑梯的倾斜角∠ABC 和∠DFE 的大小有什么关系？[答案] ∠ABC 与∠DEF 是互余的．[详细答案] 解： 在Rt △ABC 和Rt △DEF 中, ⎩⎨⎧==DFAC EFBC∴△ABC ≌△DEF ∴∠ABC=∠DEF ∵∠DEF+∠DFE=90°∴∠ABC+∠DFE=90°． ∴∠ABC 与∠DEF 是互余的．例4.AE ⊥BC ，DF ⊥BC ，E ，F 是垂足，且AE=DF ，AB=DC ，求证：∠ABC=∠DCB.[答案]∠ABC=∠DCB ．[详细答案]证明：∵AE ⊥BC ，DF ⊥BC ，∴∠AEB=∠CFD=90° 在Rt △ABE 和Rt △DCF 中， ∵AE=DF,AB=DC∴Rt △ABE ≌Rt △DCF ∴∠ABC=∠DCB ．例5. AB=CD ，AE ⊥BC ，DF ⊥BC ，垂足分别为E ，F ，CE=BF.求证：AB ∥CD ．[答案]AB ∥CD ．[详细答案]证明：CE=BF ，所以CE+EF=BF+EF ， 即BE=CF ，在Rt △AEB 和Rt △DCF 中， ,,AB CD BE CF =⎧⎨=⎩ ∴△ABE ≌△DCF ，所以∠B=∠C ， ∴AB ∥CD ．例6.在△ABC 中，∠B=∠C ，D 是BC 中点，DE ⊥AB ，DF ⊥AC ，E ，F 为垂足，求证：AD 平分∠BAC ． [答案]AD 平分∠BAC. [详细答案]证明：DF ⊥AC ，DE ⊥AB ，所以∠BED=∠CFD=90°。

直角三角形全等的判定（HL）
课型：新授课
【教学内容】直角三角形全等的判定（HL）
【学习目标】
1.知识与技能：
（1）探索并掌握直角三角形全等的判定方法“HL”；
（2）能够合理选择恰当的直角三角形判定方法来解决问题。

2.过程与方法：
经历探索直角三角形全等判定方法的过程，体会利用操作、证明、归纳获得数学结论的过程，培养学生反思的习惯和理性的思维习惯。

3.情感态度与价值观：
通过探究与交流，解决一些问题，获得成功的体验，进一步激发探究的积极性。

【学习重点】掌握判定两个直角三角形全等的特殊方法-HL。

【学习难点】灵活应用直角三角形的判定方法解决问题。

【教法学法】探究、讨论、归纳法
【教学准备】直角三角形板、两张透明纸、圆规直尺
【课时安排】1课时
【教学流程】
预习提纲
如果两个直角三角形满足斜边一条直角边分别相等，那么这两个直角三角形全等吗？
二、自主学习、合作探究（时间：10分钟）
探究：动手画一画（小组比较）
△ABC,∠C=90°，再画一个Rt△A´B´C´，使得∠
;
在收假之际老师给同学们带来了红包的祝福
达到本节课的目标；同时也来展
( )
，还需一个什么条件？
作业设计
教学反思：。

第十二章全等三角形11.2.4 直角三角形全等判定（HL）教学内容本节课主要内容是探究直角三角形的判定方法．教学目标1．知识与技能在操作、比较中理解直角三角形全等的过程，并能用于解决实际问题．2．过程与方法经历合作探索直角三角形全等判定的过程，掌握数学方法，提高合作交流,动手操作,合情推理的能力．3．情感、态度与价值观培养几何推理意识，激发学生求知欲，感悟几何思维的内涵．重、难点与关键1．重点：理解利用“斜边、直角边”来判定直角三角形全等的方法．2．难点：培养有条理的思考能力，正确使用“综合法”表达．3．关键：判定两个三角形全等时，•要注意这两个三角形中已经具有一对角相等的条件，只需找到另外两个条件即可．教具准备展台、幻灯片、直尺、圆规．教学方法采用“问题探究”的教学方法，让学生在互动交流中领会知识．教学过程一、新课导入【问题探究】问题1：如图，舞台背景的形状是两个直角三角形，工作人员想知道这两个直角三角形是否全等，但每个三角形都有一条直角边被花盆遮住无法测量.【教师活动】提出“问题探究”，组织学生讨论．（1）你能帮他想个办法吗？【学生活动】小组讨论，发表意见方法一：测量斜边和一个对应的锐角. (AAS)方法二：测量没遮住的一条直角边和一个对应的锐角. (ASA)或(AAS)（1）如果他只带了一个卷尺，能完成这个任务吗？工作人员测量了每个三角形没有被遮住的直角边和斜边，发现它们分别对应相等，于是他就肯定“两个直角三角形是全等的”.你相信他的结论吗？【教学形式】分组，合作、讨论．【探究】 任意画出一个Rt △ABC ，使∠C=90°，再画一个Rt•△A ′B ′C ′，使B ′C ′=BC ，A ′B ′=AB ，把画好的Rt △A ′B ′C ′剪下，放到Rt △ABC 上，•它们全等吗？【学生活动】画图分析，寻找规律．如下：规律：斜边和一条直角边对应相等的两个直角三角形全等（简写成“斜边、直角边”或“HL ”）．画一个Rt △A ′B ′C ′，使B ′C ′=BC,AB=AB;1．画∠MC ′N=90°。

《直角三角形全等的判定》教学设计房莎莉一、教学目标1.知识与技能(1)通过本节的教学使学生理解“HL”公理，掌握它的几何语言表达；(2)能灵活运用“HL”来判定两个直角三角形全等。

2.过程与方法(1)通过观察、实验、猜想、探索等活动，发展学生的推理能力；(2)向学生渗透“类比推理”的数学思想方法。

3.情感态度与价值观创设生活情境激发学生对数学的好奇心、求知欲，并在用数学知识解答实际问题的活动中获取成功的体验，提高学习数学的兴趣。

二、教学重难点1.重点：“斜边、直角边”的公理的证明和应用；2.难点：使用“HL”公理需要在两个直角三角形中，通过逐一证明的一组斜边和一组直角边分别相等可证两个Rt△全等，进而综合运用全等三角的性质和等式的基本性质来证明边、角相等。

三、教学流程活动流程活动内容和目的活动1 复习诊断温故知新从实例复习“SSS、SAS、ASA、AAS”和直角三角形，提出两个直角三角形是否在特殊条件下全等的问题。

活动2 探索发现合作探究已知一个直角三角形，通过画图，满足斜边和一条直角边相等的两个条件，并猜想这两个三角全等。

活动3 动手实践类比推理实验操作来证明全等，利用类比推理思想写出“HL”的几何语言。

活动4 知识延伸灵活应用反馈练习并得出推论，加深对“HL”的理解和应用活动5 总结归纳提升认识回顾梳理，从知识和能力方面总结本节课所学到的东西。

四、教与学互动设计温故知新师生行为设计意图活动1：复习诊断（1）说出三角形全等的判定方法，和它们的共同点。

（2）直角三角形ABC ，可记作？（3）复习诊断，判断对错如图，具有下列条件的Rt△ABC与Rt△A'B'C'是否全等（其中∠C＝∠C′＝教师演示课件和图片教师提出问题：（1）说出三角形全等的判定方法：答：SSS 、SAS 、ASA 、AAS（2）直角三角形ABC ，可记作并指出直角边和斜边是哪条。

答：Rt△ABC从已学的知识入手，创设问题情境，激发学生的求知欲和学习兴趣。

课题：12.2.4直角三角形全等的判定（HL）课型：新授课【教学内容】直角三角形全等的判定（HL）【学习目标】1.知识与技能：（1）探索并掌握直角三角形全等的判定方法“HL”；（2）能够合理选择恰当的直角三角形判定方法来解决问题。

2.过程与方法：经历探索直角三角形全等判定方法的过程，体会利用操作、证明、归纳获得数学结论的过程，培养学生反思的习惯和理性的思维习惯。

3.情感态度与价值观：通过探究与交流，解决一些问题，获得成功的体验，进一步激发探究的积极性。

【学习重点】掌握判定两个直角三角形全等的特殊方法-HL。

【学习难点】灵活应用直角三角形的判定方法解决问题。

【教法学法】探究、讨论、归纳法【教学准备】直角三角形板、两张透明纸、圆规直尺【课时安排】1课时【教学流程】预习提纲1.斜边与一条直角边分别相等的两个直角三角形.（简写成“”或“”）.2.如图，△ABC中，AB=AC，AD是高，则△ADB与△ADC （填“全等”或“不全等”）根据（用简写法）.3.略.4.课后练习题……（略）.课堂流程教案一、情境导入、目标引领（时间：5分钟）1、判定两个三角形全等的方法有：、、、。

2、这些方法能判定直角三角形全等吗？3、思考：对于两个直角三角形，除了直角相等外，还要添几个条件，这两个直角三角形就全等呢？我们知道直角三角形是特殊的三角形，所以可以用一般三角形全等的判定方法: SSS 、SAS、ASA、AAS。

只要添加一边一锐角或两直角边分别相等，这两个直角三角形就全等了。

4.问题：如果两个直角三角形满足斜边和一条直角边分别相等，那么这两个直角三角形全等吗？二、自主学习、合作探究（时间：10分钟）探究：动手画一画（小组比较）1．任意画出一个Rt△ABC,∠C=90°，再画一个Rt△A´B´C´，使得∠C´= 90°，B´C´=BC，A´B´= AB。

12.2.4直角三角形全等的判定(HL)教学设计一、教学目标：1.探索并理解直角三角形全等的判定方法“HL”．2.会用直角三角形全等的判定方法“HL”判定两个直角三角形全等．二、教学重、难点：重点：掌握判定两个直角三角形全等的特殊方法-HL．难点：熟练选择判定方法，判定两个直角三角形全等．三、教学准备：课件、三角尺、圆规等。

四、教学过程：复习回顾1.判定两个三角形全等方法____________________.2.如图，AB⊥BE于B，DE⊥BE于E.(1)若∠A=∠D，AB=DE.则与△DEF______(填“全等”或“不全等”)根据______(用简写法).(2)若∠A=∠D，BC=EF.则△ABC与△DEF______(填“全等”或“不全等”)根据______(用简写法).(3)若AB=DE，BC=EF.则△ABC与△DEF_______(填“全等”或“不全等”)根据______(用简写法).若AB=DE，AC=DF，此时△ABC与△DEF还会全等吗？知识精讲探究：任意画出一个Rt△ABC，使∠C=90°，再画一个Rt△A′B′C′，使得∠C′=90°，B′C′=BC，A′B′=A B.把画好的Rt△A′B′C′剪下，放到Rt△ABC上，它们全等吗？斜边和一条直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).注意：(1)“HL”定理是仅适用于Rt△的特殊方法.因此，判定两个直角三角形全等的方法除了可以使用“SSS”、“SAS”、“ASA”、“AAS”外还可以使用“HL”.(2)应用HL定理时，虽只有两个条件，但必须先有两个Rt△.书写格式为：在Rt△ABC和Rt△A′B′C′中，==AB A B BC B C′′′′∴Rt△ABC≌Rt△A′B′C′(HL)典例解析例1.如图，AC⊥BC，BD⊥AD，垂足分别为C，D，AC=B D.求证BC=AD.证明：∵AC ⊥BC ，BD ⊥AD ，∴∠C 与∠D 都是直角，在Rt △ABC 和Rt △BA D 中，BDAC BA AB ∴Rt △ABC ≌Rt △BAD (HL)，∴BC =AD.【针对练习】如图，C 是路段AB 的中点，两人从C 同时出发，以相同的速度分别沿两条直线行走，并同时到达D 、E 两地.DA ⊥AB ，EB ⊥A B.D ，E 与路段AB 的距离相等吗？为什么？解：AD =BE ，理由如下：依题意可得，AC =BC ，CD =CE .∵DA ⊥AB ，EB ⊥AB ，∴∠A =∠B =90°，在Rt △ACD 和Rt △BCE 中，BCAC CE CD ∴Rt △ACD ≌Rt △BCE (HL)，∴AD =BE.例2.如图，AC ⊥AD ，BC ⊥BD ，AC=BD ，求证：AD=BC .证明:连接D C.∵AC ⊥AD ，BC ⊥BD ，∴∠A =∠B =90°，在Rt △ADC 和Rt △BC D 中，AB BA AC BD∴Rt △ADC ≌Rt △BCD (HL)，∴AD =BC.【针对练习】已知：如图，AB ，AD DC ，AB AD ，求证：BC DC ．证明：连接AC,如下图，∵AB ⊥BC,AD ⊥DC,∴∠B =∠D =90°,在Rt △ABC 和Rt △AD C 中，AC AC AD AB∴Rt △ABC ≌Rt △ADC (HL),∴BC =BD.例3.如图，已知AD 是△ABC 的角平分线,且BD =CD ，DE 、DF 分别垂直于AB 、AC ，垂足分别为E 、F .求证BE =CF.证明:AD 平分∠BAC ，∴∠BAD =∠CAD ，∵DE 、DF 分别垂直于AB 、AC ，∴∠AED =∠AFD =90°，在△AED 和△AFD 中，AED AFD EAD FAD AD AD∴△AED ≌△AFD (AAS)，∴DE =DF ，在Rt △BDE 和Rt △CDF 中，BD CD DE DF∴Rt △BDE ≌Rt △CDF （HL ），∴BE =CF .【针对练习】已知：如图，点A 、E 、C 同一条直线上，AB ⊥BC ，AD ⊥DC ，AB ＝A D ．求证：BE ＝DE．证明：∵AB ⊥BC ，AD ⊥DC ，∴在Rt ABC 与Rt ADC 中，AB AD AC AC，∴Rt ABC ADC ≌R t （HL ），∴∠BAE ＝∠DAE ，在ABE △与ADE 中，AB AD BAE DAE AE AE，∴ABE ADE ≌（SAS ），∴BE ＝DE ．例4.如图，在△AB C 中，∠C ＝90°，AD 是∠CAB 的角平分线，DE ⊥AB 于E ，点F 在边AC 上，连接DF ．（1）求证：AC ＝AE ；（2）若DF ＝DB ，试说明∠B 与∠AFD 的数量关系；（3）在（2）的条件下，若AB ＝m ，AF ＝n ，求BE 的长（用含m ，n 的代数式表示）．（1）证明：∵∠C ＝90°，DE ⊥AB ，∴∠C ＝∠AED ＝90°，在△ACD 和△AE D 中，C AED CAD EAD AD AD，∴△ACD ≌△AED （AAS ），∴AC ＝AE ；（2）解：∠B +∠AFD ＝180°，理由如下：由（1）得：△ACD ≌△AED ，∴DC ＝DE ，在Rt △CDF 和Rt △ED B 中，DC DE DF DB，∴Rt△CDF≌Rt△EDB（HL），∴∠CFD＝∠B，∵∠CFD+∠AFD＝180°，∴∠B+∠AFD＝180°；（3）解：由（2）知，Rt△CDF≌Rt△EDB，∴CF＝BE，由（1）知AC＝AE，∵AB＝AE+BE，∴AB＝AC+BE，∵AC＝AF+CF，∴AB＝AF+2BE，∵AB＝m，AF＝n，∴BE＝12（m﹣n）．课堂小结1.本节课你有哪些收获？2.还有没解决的问题吗？【设计意图】培养学生概括的能力。

《直角三角形全等的判定》参考教案直角三角形全等的判定教学目标1、经历探究直角三角形全等条件的过程，体会利用操作、归纳获得数学结论的过程；2、把握直角三角形全等的条件，并能运用其解决一些实际问题。

3、在探究直角三角形全等条件及其运用的过程中，能够进行有条理的摸索并进行简单的推理。

教学重点运用直角三角形全等的条件解决一些实际问题。

教学难点熟练运用直角三角形全等的条件解决一些实际问题。

教学过程Ⅰ．提出问题，复习旧知1、判定两个三角形全等的方法：、、、2、如图，Rt△ABC中，直角边是、，斜边是3、如图，AB⊥BE于C，DE⊥BE于E，（1）若∠A=∠D，AB=DE，则△ABC与△DEF （填“全等”或“不全等” ）依照（用简写法）（2）若∠A=∠D，BC=EF，则△ABC与△DEF （填“全等”或“不全等” ）依照（用简写法）（3）若AB=DE，BC=EF，则△ABC与△DEF （填“全等”或“不全等” ）依照（用简写法）（4）若AB=DE，BC=EF，AC=DF则△ABC与△DEF （填“全等”或“不全等” ）依照（用简写法）Ⅱ．导入新课（一）探究练习：（动手操作）：已知线段a ，c (a<c) 和一个直角α利用尺规作一个Rt△ABC，使∠C=∠α，AB=c ，CB= a1、按步骤作图： a c①作∠MCN=∠α=90°，②在射线CM上截取线段CB=a，③以B 为圆心，C为半径画弧，交射线CN于点A，α④连结AB2、与同桌重叠比较，是否重合？3、从中你发觉了什么？斜边与一直角边对应相等的两个直角三角形全等．（ＨＬ）（二）巩固练习：1．如图，△ABC中，AB=AC，AD是高，则△ADB与△ADC （填“全等”或“不全等” ）依照（用简写法）2．如图，CE⊥AB，DF⊥AB，垂足分别为E、F，（1）若AC//DB，且AC=DB，则△ACE≌△BDF，依照（2）若AC//DB，且AE=BF，则△ACE≌△BDF，依照（3）若AE=BF，且CE=DF，则△ACE≌△BDF，依照（4）若AC=BD，AE=BF，CE=DF。

三角形全等的判定导学案（HL）人教版数学
课题：«11.2三角形全等的判定»(HL)导学案
运用说明：先生应用自习先预习课本第13、14页10分钟，然后35分钟独立做完学案。

正课由小组讨论交流10分钟，25分钟展现点评，10分钟整理落实，关于有疑问的标题教员点拨、拓展。

【学习目的】
1、了解直角三角形全等的判定方法HL，并能灵敏选择方法判定三角形全等;
2.经过独立思索、小组协作、展现质疑，体会探求数学结论的进程，开展合情推理才干;
3. 极度热情、高度责任、自动自发、享用成功。

教学重点：运用直角三角形全等的条件处置一些实践效果。

教学难点：熟练运用直角三角形全等的条件处置一些实践效果。

【学习进程】
一、自主学习
1、温习思索
(1)、判定两个三角形全等的方法：、、、
(2)、如图，Rt△ABC中，直角边是、，斜边是
(3)、如图，ABBE于B，DEBE于E，
①假定D，AB=DE，
那么△ABC与△DEF (填全等或不全等 )
依据 (用简写法)
②假定D，BC=EF，
那么△ABC与△DEF (填全等或不全等 )
依据 (用简写法)
③假定AB=DE，BC=EF，
那么△ABC与△D EF (填全等或不全等 )依据 (用简写法) ④假定AB=DE，BC=EF，AC=DF
那么△ABC与△DEF (填全等或不全等 )依据 (用简写法) 2、假设两个直角三角形满足斜边和一条直角边对应相等，这两个直角三角形全等吗?
(1)入手试一试。

：Rt△ABC。

《直角三角形全等的判定》教学设计中心发言人：DH教学目标:（1）明确两个直角三角形的全等，可以利用“边边边，边角边，角边角，角角边”来证明；但是由于直角相等，所以两个直角三角形全等的判定，只需要增加两个条件即可。

（2）探索和掌握直角三角形全等的特殊判定方法：斜边和一条直角边对应相等的两个直角三角形全等，并会用“SSS，SAS，ASA，AAS及HL”证明两个直角三角形全等。

教学重点：探索和掌握直角三角形全等的特殊判定方法：斜边和一条直角边对应相等的两个直角三角形全等，并会用“SSS，SAS，ASA，AAS及HL”证明两个直角三角形全等。

教学难点：（1）满足“边边角”分别对应相等的两个三角形不一定全等，但满足“斜边和一条直角边对应相等的两个直角三角形”符合“边边角”的条件，两个直角三角形却是全等的。

（2）要注意用HL直角三角形全等的证明格式集体备教教学过程：1、复习与回顾：（1）判定两个三角形全等的方法是，，，（2）回顾直角三角形的边、角的名称及相关性质。

2、尝试归纳两个直角三角形全等的判定方法：如图，AB⊥BE于B，D E⊥BE于E，（1）若∠A=∠D，AB=DE，则△ABC与△DEF （填“全等”或“不全等”），根据（用简写法）。

（2）若∠A=∠D，BC=EF，则△ABC与△DEF （填“全等”或“不全等”），个性补教AB CE FD根据（用简写法）。

（3）若AB=DE，BC=EF，则△ABC与△DEF （填“全等”或“不全等”），根据（用简写法）。

（4）若∠A=∠D，AC=DF则△ABC与△DEF （填“全等”或“不全等”），根据（用简写法）。

归纳：两个直角三角形全等的类型：ASA ,AAS ,SAS ,AAS (一锐角一直角边，一锐角一斜边，两直角边，共四种情形) 3、探究：一斜边一直角边对应相等，两直角三角形是否全等？（1）情景引入如图，两根长度为12米的绳子，一端系在旗杆上，另一端分别固定在地面两个木桩上，两个木桩离旗杆底部的距离相等吗？请说明你的理由。

《三角形全等的判定》第四课时（HL）教案12.2.4三角形全等的判定（4）【教学目标】：1、知识与技能：直角三角形全等的条件：“斜边、直角边”．2、过程与方法：1）．经历探究直角三角形全等条件的过程，体会一般与特殊的辩证关系．2）．掌握直角三角形全等的条件：“斜边、直角边”．3）．能运用全等三角形的条件，解决简单的推理证明问题．3、情感态度与价值观：通过画图、探究、归纳、交流使学生获得一些研究问题的经验和方法．发展实践能力和创新精神【教学情景导入】：提出问题，复习旧知1、判定两个三角形全等的方法：、、、2、如图，Rt△ABC中，直角边是、，斜边是3、如图，AB⊥BE于C，DE⊥BE于E，（1）若∠A=∠D，AB=DE，则△ABC与△DEF（填“全等”或“不全等” ）根据（用简写法）（2）若∠A=∠D，BC=EF，则△ABC与△DEF（填“全等”或“不全等” ）根据（用简写法）（3）若AB=DE，BC=EF，则△ABC与△DEF（填“全等”或“不全等” ）根据（用简写法）（4）若AB=DE，BC=EF，AC=DF则△ABC与△DEF（填“全等”或“不全等” ）根据（用简写法）创设情境，导入新课如图，舞台背景的形状是两个直角三角形，工作人员想知道这两个直角三角形是否全等，但两个三角形都有一条直角边被花盆遮住无法测量．（播放课件）（1）你能帮他想个办法吗？（2）如果他只带了一个卷尺，能完成这个任务吗？（1）[生]能有两种方法．第一种方法：用直尺量出斜边的长度，再用量角器量出其中一个锐角的大小，若它们对应相等，根据“AAS”可以证明两直角三角形是全等的．第二种方法：用直尺量出不被遮住的直角边长度，再用量角器量出其中一个锐角的大小，若它们对应相等，根据“ASA”或“AAS”，可以证明这两个直角三角形全等．可是，没有量角器，只有卷尺，那么他只能量出斜边长度和不被遮住的直角边边长，可是它们又不是“两边夹一角的关系”，所以我没法判定它们全等．[师]这位师傅量了斜边长和没遮住的直角边边长，发现它们对应相等，于是他判断这两个三角形全等．你相信吗？导入新课[生]这两个三角形都是直角三角形，也许是全等的．因为它还有直角这个特殊条件．[师]有道理．但科学是严密的，今天我们就来探究“两个直角三角形全等的条件”．做一做：已知线段AB=5cm，BC=4cm和一个直角，利用尺规做一个直角三角形，使∠C=?90°，AB作为斜边．做好后，将△ABC剪下与同伴比较，看能发现什么规律？（学生自主完成后，与同伴交流作图心得，然后由一名同学口述作图方法．老师做多媒体课件演示，激发学习兴趣）．作法：第一步：作∠MCN=90°．第二步：在射线CM 上截取CB=4cm ．第三步：以B 为圆心，5cm 为半径画弧交射线CN 于点A ．第四步：连结AB ．就可以得到所想要的Rt △ABC ．（如下图所示）将Rt △ABC 剪下，同一组的同学做的三角形叠在一起，发现这些三角形全等．可以验证，对一般的直角三角形也有这样的规律．探究结果总结：斜边和一条直角边对应相等的两个直角三角形全等（可以简写成“斜边、直角边”和“HL”）．[师]你能用几种方法说明两个直角三角形全等呢？[生]直角三角形也是三角形，一般来说，可以用“定义、SSS 、SAS 、?ASA ?、?AAS”这五种方法，但它又具有特殊性，还可以用“HL”的方法判定．[师]很好，两直角三角形中由于有直角相等的条件，所以判定两直角三角形全等只须找两个条件，但这两个条件中至少要有一个条件是一对对应边才行．【教学过程设计】：[例1]如图，AC ⊥BC ，BD ⊥AD ，AC=BD ．求证：BC=AD ．分析：BC 和AD 分别在△ABC 和△ABD 中，所以只须证明△ABC ≌△BAD ，?就可以证明BC=AD 了．证明：∵AC ⊥BC ，BD ⊥AD∴∠D=∠C=90°在Rt △ABC 和Rt △BAD 中AB AB AC BD=??=?∴Rt △ABC ≌Rt △BAD （HL ）∴BC=AD ．[例2]有两个长度相等的滑梯，左边滑梯的高AC ?与右边滑梯水平方向的长度DF 相等，两滑梯倾斜角∠ABC 和∠DFE 有什么关系？[师生共析]∠ABC 和∠DFE 分别在Rt △ABC 和Rt △DEF 中，?已知条件中这两个三角形又有一些对应的等量关系，所以可以证明这两个三角形全等得到对应角相等，显然，可以看出这两个角不相等，它们又是直角三角形中的锐角，是不是互余呢？我们试试看．证明：在Rt △ABC 和Rt △DEF 中BC EF AC DF=??=? 所以Rt △ABC ≌Rt △DEF （HL ）∴∠ABC=∠DEF又∵∠DEF+∠DFE=90°∴∠ABC+∠DFE=90°即两滑梯的倾斜角∠ABC 与∠DFE 互余．【教学反思】通过本节学习，我们有如下收获：1．直角三角形是特殊的三角形，所以不仅有一般三角形判定全等的方法，?而且还有直角三角形特殊的判定方法──“HL”．2．两个直角三角形中，由于有直角相等的条件，?所以判定两个直角三角形全等，只须找两个条件（两个条件中至少有一个条件是一对对应边相等）即可．至此，我们有六种判定三角形全等的方法：1）．全等三角形的定义2）．边边边（SSS ）3）．边角边（SAS ）4）．角边角（ASA ）5）．角角边（AAS ）6）．HL （仅用在直角三角形中）。