数电复习141502
- 格式:pdf
- 大小:7.13 MB
- 文档页数:35

数制和编码先介绍常见的十进制数,然后介绍二进制、十六进制,再介绍各进制数的相互转换,最后讲述十进制的二进制编码形式.一、十进制数:按照进位方式进行计数的制度称进位计数制.进位计数制中有两个基本要素:基数和权值.十进制数的基数是10(0~9),权值是10i(i是数字所处位置的序号)。
特点是逢10进1。
例:(567.8)10=5×102+6×101+7×100+8×10-1二、二进制数:计算机内部使用的数值符号只有两个:0和1。
外界的各种信息(数字、符号、图像)到了计算机内部都由0、1两个数字组成。
二进制数的基数是2,权值是2i,特点是逢2进1。
例:(101101。
1)2=1×25+0×24+1×23+1×22+0×21+1×20+1×2—1=32+8+4+1+0。
5=45.5三、十六进制数:二进制数的缺点是位数多,不易书写和记忆,为此我们常采取十六进制数。
十六进制数的基数是16(0~9,A~F),位权是16i。
特点是逢十六进一。
例:(2B.A)16=2×16+11×1+10/16=(43.625)104B7+84C=(D03)16四、数制转换:1.任意R进制数转换成十进制数:只需将其按权展开的多项式求和.例:(11011。
01)2=1×24+1×23+0×22+1×21+1×20+0×2—1+1×2—2=(27.25)10(FC)16=15×161+12×160=(252)102。
十进制数转换成二进制数:分为整数部分和小数部分。
整数部分采取“除基取余法”:将要转换的十进制整数除以2,取余数作为二进制整数的最低位K0,将商继续除以2,再取商的余数作为次低位K1,这样不断除,直到商为0,最后的余数作为二进制整数的最高位Kn。
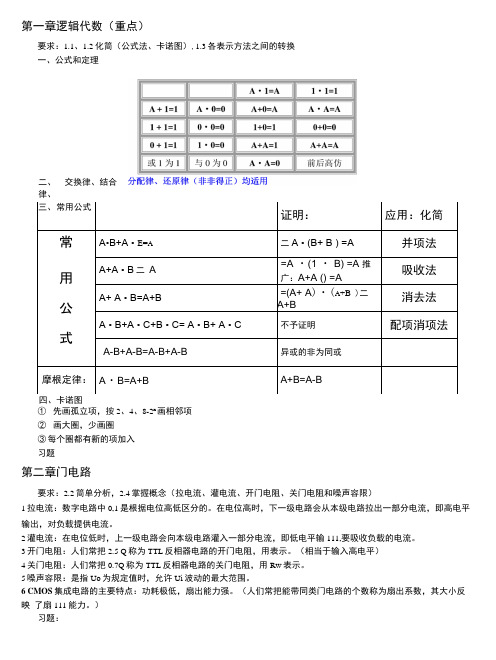
第一章逻辑代数(重点)要求:1.1、1.2化简(公式法、卡诺图),1.3各表示方法之间的转换 一、公式和定理① 先画孤立项,按2、4、8-2n 画相邻项 ② 画大圈,少画圈 ③ 每个圈都有新的项加入 习题第二章门电路要求:2.2简单分析,2.4掌握概念(拉电流、灌电流、开门电阻、关门电阻和噪声容限)1拉电流:数字电路中0,1是根据电位高低区分的。
在电位高时,下一级电路会从本级电路拉出一部分电流,即高电平输出,对负载提供电流。
2灌电流:在电位低时,上一级电路会向本级电路灌入一部分电流,即低电平输111,要吸收负载的电流。
3开门电阻:人们常把2.5 Q 称为TTL 反相器电路的开门电阻,用表示。
(相当于输入高电平) 4关门电阻:人们常把0.7Q 称为TTL 反相器电路的关门电阻,用Rw 表示。
5噪声容限:是指Uo 为规定值时,允许Ui 波动的最大范围。
6 CMOS 集成电路的主要特点:功耗极低,扇出能力强。
(人们常把能带同类门电路的个数称为扇出系数,其大小反映 了扇111能力。
)习题:证明:应用:化简 常 用 公 式A•B+A • E=A 二A • (B+ B ) =A并项法 A+A • B 二 A =A ・(1 ・ B) =A 推广:A+A () =A 吸收法 A+ A • B=A+B=(A+ A )・(A +B )二A+B消去法 A • B+A • C+B • C= A • B+ A • C不予证明 配项消项法A-B+A-B=A-B+A-B异或的非为同或摩根定律: A ・B=A+BA+B=A-B二、 交换律、结合律、三、 常用公式四、卡诺图第三章组合逻辑电路要求:3」分析和设计方法,3.2全加器各引脚功能,半加器概念,322、3.3、3.4功能表和简单拓展,不看原理, 3.5 (难点)会例题即可0 分析方法:圖辑图I-圖辑痕送式一化简-I真值表I-说明功能设计方法:逻辑抽象一匱歴一亶裹亘一化简一壓图辺半加:两个1位二进制数相加,叫做半加。


数字电路期末总复习知识点归纳详细第 1 章数字逻辑概论一、进位计数制1.十进制与二进制数的转换2.二进制数与十进制数的转换3.二进制数与16进制数的转换二、基本逻辑门电路第 2 章逻辑代数表示逻辑函数的方法,归纳起来有:真值表,函数表达式,卡诺图,逻辑图及波形图等几种。
一、逻辑代数的基本公式和常用公式1)常量与变量的关系A+0=A与A1 AA +1= 1 与A0 0A A= 1 与 A A= 02)与普通代数相运算规律a.交换律:A+B=B+AAB BAb.结合律:(A+B) +C=A+(B +C)(A B) C A (B C)c.分配律: A (B C)= A B A CA B C (A B)() A C))3)逻辑函数的特殊规律a.同一律:A +A +Ab.摩根定律: A B A B, A B A Bb.关于否定的性质A= A二、逻辑函数的基本规则代入规则在任何一个逻辑等式中,如果将等式两边同时出现某一变量A的地方,都用一个函数L表示,则等式仍然成立,这个规则称为代入规则例如: A B C A B C可令L=B C则上式变成A L A L = A L A B C三、逻辑函数的:——公式化简法公式化简法就是利用逻辑函数的基本公式和常用公式化简逻辑函数,通常,我们将逻辑函数化简为最简的与—或表达式1)合并项法:利用A + A A 1 或 A B A B A , 将二项合并为一项,合并时可消去一个变量例如:L=A BC ABC AB(C C) AB2)吸收法利用公式 A A B A,消去多余的积项,根据代入规则 A B可以是任何一个复杂的逻辑式例如化简函数L=AB AD BE解:先用摩根定理展开:AB = A B 再用吸收法L=AB AD BE= A B AD BE=(A AD) (B BE)=A(1 AD ) B(1 BE)AB3)消去法利用 A AB A B 消去多余的因子例如,化简函数L=A B AB ABE ABC解:L=AB AB ABE ABC=(AB ABE) (AB ABC)=A(B BE) A(B BC)=A(B C)( B B) A(B B)( B C)= A(B C) A(B C)= AB AC AB AC= AB AB C4)配项法利用公式 A B A C BC A B A C 将某一项乘以( A A),即乘以1,然后将其折成几项,再与其它项合并。
数字电路技术基础复习提纲1 逻辑代数基础1.1 概述1、什么是模拟信号?什么是数字信号?严格说来,自然界中存在的信号都是模拟信号,数字信号是人为的抽象出来的在时间上不连续的电信号,就是用一系列的矩形波来表示一个数字。
因此数字信号有两种,一是用模拟信号直接转换而来,用数字表示模拟信号在不同时刻的量化值;二是为控制、处理等目的人为产生的。
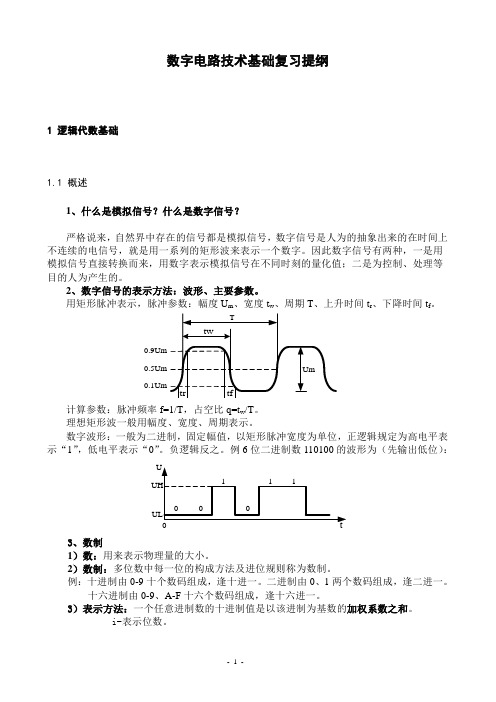
2、数字信号的表示方法:波形、主要参数。
用矩形脉冲表示,脉冲参数:幅度U m、宽度t w、周期T、上升时间t r、下降时间t f。
0.9Um0.5Um0.1Um计算参数:脉冲频率f=1/T,占空比q=t w/T。
理想矩形波一般用幅度、宽度、周期表示。
数字波形:一般为二进制,固定幅值,以矩形脉冲宽度为单位,正逻辑规定为高电平表示“1”,低电平表示“0”。
负逻辑反之。
例6位二进制数110100的波形为(先输出低位):3、数制1)数:用来表示物理量的大小。
2)数制:多位数中每一位的构成方法及进位规则称为数制。
例:十进制由0-9十个数码组成,逢十进一。
二进制由0、1两个数码组成,逢二进一。
十六进制由0-9、A-F十六个数码组成,逢十六进一。
3)表示方法:一个任意进制数的十进制值是以该进制为基数的加权系数之和。
i-表示位数。
k i -表示第i 位的系数,可以是该进制数码中的任意一个。
r i -表示第i 位的权值,r 是该进制的基数。
n-表示整数位。
m-表示小数位。
4、常用数制的转换方法 1)十-二转换、二-十转换十-二转换:求加权系数公式中各位的系数,对十进制数的整数和小数分别转换。
整数部分的权是乘2关系,转换时需除2。
小数部分的权是除2关系,转换时需乘2。
例:将25.625转换为二进制数① 整数部分:连续除2,取余数,直到商为0。
252222212631010011低位②小数部分:连续乘2,取整数,直到要求的精度为至。
20.6251.25020.50021.000110高位低位(25.625)10=(11001.101)2 二-十转换:求加权系数和。

数字电子技术基础总复习要点数字电子技术基础总复习要点一、填空题第一章1、变化规律在时间上和数量上都是离散是信号称为数字信号。
2、变化规律在时间或数值上是连续的信号称为模拟信号。
3、不同数制间的转换。
4、反码、补码的运算。
5、8421码中每一位的权是固定不变的,它属于恒权代码。
6、格雷码的最大优点就在于它相邻两个代码之间只有一位发生变化。
第二章1、逻辑代数的基本运算有与、或、非三种。
2、只有决定事物结果的全部条件同时具备时,结果才发生。
这种因果关系称为逻辑与,或称逻辑相乘。
3、在决定事物结果的诸条件中只要有任何一个满足,结果就会发生。
这种因果关系称为逻辑或,也称逻辑相加。
4、只要条件具备了,结果便不会发生;而条件不具备时,结果一定发生。
这种因果关系称为逻辑非,也称逻辑求反。
5、逻辑代数的基本运算有重叠律、互补律、结合律、分配律、反演律、还原律等。
举例说明。
6、对偶表达式的书写。
7、逻辑该函数的表示方法有:真值表、逻辑函数式、逻辑图、波形图、卡诺图、硬件描述语言等。
8、在n变量逻辑函数中,若m为包含n个因子的乘积项,而且这n个变量均以原变量或反变量的形式在m中出现一次,则称m为该组变量的最小项。
9、n变量的最小项应有2n个。
10、最小项的重要性质有:①在输入变量的任何取值下必有一个最小项,而且仅有一个最小项的值为1;②全体最小项之和为1;③任意两个最小项的乘积为0;④具有相邻性的两个最小项之和可以合并成一项并消去一对因子。
11、若两个最小项只有一个因子不同,则称这两个最小项具有相邻性。
12、逻辑函数形式之间的变换。
(与或式—与非式—或非式--与或非式等)13、化简逻辑函数常用的方法有:公式化简法、卡诺图化简法、Q-M法等。
14、公式化简法经常使用的方法有:并项法、吸收法、消项法、消因子法、配项法等。
15、卡诺图化简法的步骤有:①将函数化为最小项之和的形式;②画出表示该逻辑函数的卡诺图;③找出可以合并的最小项;④选取化简后的乘积项。
数字电路期末总复习知识点归纳详细一、简述亲爱的小伙伴们,又是一年一度的期末复习时刻来临了,这次复习的主角是数字电路知识。
让我们一起来看看哪些内容是重点,助力你的复习之旅吧!数字电路虽然听起来高大上,但其实与我们日常生活息息相关。
手机、电视、电脑等电子产品都离不开它。
因此掌握好数字电路知识,不仅对学习有帮助,还能更好地理解生活中的科技应用。
首先你得清楚数字电路的基本概念,比如什么是数字信号、什么是模拟信号。
这可是基础中的基础,得打好基础才能建起高楼大厦。
接下来是数字电路的逻辑门和逻辑代数,这些看似复杂的名词其实背后都有简单的逻辑原理,只要理解了就容易掌握。
别忘了组合逻辑和时序逻辑电路,它们是数字电路的核心部分,考试中的大题往往围绕它们展开。
此外数制与编码也不可忽视,它们在数字电路中有着举足轻重的作用。
1. 回顾本学期数字电路课程的重要性这个学期数字电路课程真是收获满满啊!时间过得飞快,转眼就要期末考试了,大家是不是觉得有必要好好复习一下呢?确实数字电路课程在电子信息技术领域可是非常关键的,这门课程就像打开了一扇神奇的大门,让我们了解了电子设备背后的秘密。
咱们学习的内容都是电子工程师必备的基础知识,对咱们未来无论是从事相关职业还是日常生活都很有帮助。
所以啊同学们,一定要重视这次的复习,为期末考试做好准备!这个段落力求简洁明了,使用口语化的表达方式,易于读者理解和接受。
同时加入了情感化的语气,增强了文章的人情味。
2. 复习目的与意义期末临近是时候开始我们的复习计划了,说到复习数字电路,可不是简单地过一遍课本,而是为了更好地掌握这门课的知识和技能,帮助大家在即将到来的期末考试中取得好成绩。
所以今天就来一起梳理下复习目的和意义,让大家明白为什么要这么认真地对待这次复习。
首先复习数字电路是为了巩固我们学过的知识,毕竟课本上的内容那么多,不可能一下子全记住。
通过复习我们可以再次梳理知识脉络,加深理解确保学过的内容都能牢牢掌握。
数电知识点总结复习数字电子技术是现代电子技术中的一个重要分支,它是指利用数字信号和数字逻辑技术进行信息的存储、处理和传输的一种技术。
数字电子技术已经深入到我们的日常生活中,无论是计算机、通信、电子设备还是家用电器,都离不开数字电子技术的支持。
因此,掌握数电知识对于电子工程师来说是非常重要的。
下面,我们就来总结一下数电知识点,帮助大家进行复习。
一、数字逻辑电路1. 布尔代数布尔代数是数字逻辑电路设计的基础。
它是一种处理逻辑关系的代数系统,其中变量的值只有“0”和“1”,运算只有“与”、“或”、“非”三种基本运算。
在数字逻辑电路设计中,可以利用布尔代数进行逻辑函数的化简和设计。
2. 逻辑门逻辑门是数字逻辑电路中最基本的电路组件,常见的逻辑门有与门、或门、非门、异或门等。
它们是按照逻辑运算的功能来设计的,可以实现逻辑运算的功能,如与门可以实现“与”运算,或门可以实现“或”运算。
3. 组合逻辑电路组合逻辑电路是由逻辑门按照一定的逻辑运算关系连接而成的电路。
在组合逻辑电路中,逻辑门的输出只取决于当前的输入信号,不受以前的输入信号和输出信号的影响。
4. 时序逻辑电路时序逻辑电路是在组合逻辑电路的基础上加入了时钟信号控制的逻辑电路。
它的输出不仅依赖于当前的输入信号,还受到时钟信号的控制,因此在时序逻辑电路中,输出信号是有记忆功能的。
5. 计数器计数器是一种能够对输入信号进行计数的时序逻辑电路。
它可以实现二进制或者十进制的计数功能,常见的计数器有同步计数器和异步计数器。
6. 寄存器寄存器是一种能够存储数据的时序逻辑电路。
它可以存储多位的二进制数据,并且能够根据控制信号对数据进行读写操作。
7. 存储器存储器是用于存储大量数据的器件,它有随机存取存储器和只读存储器两种类型。
随机存取存储器可以对数据进行读写操作,而只读存储器只能读取数据,不能进行写操作。
8. 逻辑运算器逻辑运算器是能够进行逻辑运算的电路,常见的逻辑运算器有加法器、减法器、乘法器、除法器等。
数字电路期末总复习知识点归纳详细第1章数字逻辑概论一、进位计数制1.十进制与二进制数的转换2.二进制数与十进制数的转换3.二进制数与16进制数的转换二、基本逻辑门电路第2章逻辑代数表示逻辑函数的方法,归纳起来有:真值表,函数表达式,卡诺图,逻辑图及波形图等几种。
一、逻辑代数的基本公式和常用公式1)常量与变量的关系A+0=A与A=⋅1AA+1=1与0⋅A0=A⋅=0A+=1与AA2)与普通代数相运算规律a.交换律:A+B=B+A⋅A⋅=BABb.结合律:(A+B)+C=A+(B+C)BA⋅⋅⋅C⋅=()A)(CBc.分配律:)⋅=+A⋅B(CA⋅A C⋅BA+B++)⋅=C)())(CABA3)逻辑函数的特殊规律a.同一律:A+A+Ab.摩根定律:BA+B⋅A=AB+,BA⋅=b.关于否定的性质A=A二、逻辑函数的基本规则代入规则在任何一个逻辑等式中,如果将等式两边同时出现某一变量A的地方,都用一个函数L表示,则等式仍然成立,这个规则称为代入规则例如:C⋅+⋅A⊕⊕ABCB可令L=CB⊕则上式变成L⋅=C+AA⋅L=⊕⊕A⊕BAL三、逻辑函数的:——公式化简法公式化简法就是利用逻辑函数的基本公式和常用公式化简逻辑函数,通常,我们将逻辑函数化简为最简的与—或表达式1)合并项法:利用A+1=⋅=A=⋅, 将二项合并为一项,合并时可消去一个变量B+ABA或AA例如:L=BBCA=(A+)+=ABCCACB2)吸收法利用公式A+,消去多余的积项,根据代入规则B⋅A⋅可以是任何一个复杂的逻BAA=辑式例如化简函数L=EA+AB+DB解:先用摩根定理展开:AB=BA+再用吸收法L=E+AB+ADB=E+BA++ADB=)AD++A+()(EBB=)AA+D++1(E1(B)B=BA+3)消去法利用B+消去多余的因子A+=BAA例如,化简函数L=ABCBA++A+EBAB解:L=ABCAA+++BBBEA=)BA+AB++(ABC)(BAE=)BEA+++BA)(B(BC=)BCBA++B+++B)((A(C)B)(B=)BA++C+A()(CB=ACA++B+ABCA=C+A+BBA4)配项法利用公式C⋅+=++⋅⋅将某一项乘以(AA⋅BBAAACBCA+),即乘以1,然后将其折成几项,再与其它项合并。