2010海南省中考数学试题及答案

2010-2014海南中考数学函数大题(含答案)D24．（14分）（2013•海南）如图10，二次函数的图象与x轴相交于点A（﹣3，0）、B（﹣1，0），与y轴相交于点C（0，3），点P是该图象上的动点；一次函数y=kx﹣4k（k≠0）的图象过点P 交x轴于点Q．（1）求该二次函数的解析式；（2）当点P的坐标为（﹣4，m）时，求证：∠OPC=∠AQC；（3）点M，N分别在线段AQ、CQ上，点M以每秒3个单位长度的速度从点A向点Q运动，同时，点N以每秒1个单位长度的速度从点C向点Q运动，当点M，N中有一点到达Q点时，两点同时停止运动，设运动时间为t秒．连接AN，当△AMN 的面积最大时，①求t的值；②直线PQ能否垂直平分线段MN？若能，请求出此时点P的坐标；若不能，请说明你的理由．图（1）解：设抛物线的解析式为：y=a（x+3）（x+1），∵抛物线经过点C（0，3），∴3=a×3×1，解得a=1．∴抛物线的解析式为：y=（x+3）（x+1）=x2+4x+3．（2）证明：在抛物线解析式y=x2+4x+3中，当x=﹣4时，y=3，∴P（﹣4，3）．∵P（﹣4，3），C（0，3），∴PC=4，PC∥x轴．∵一次函数y=kx﹣4k（k≠0）的图象交x轴于点Q，当y=0时，x=4，∴Q（4，0），OQ=4．∴PC=OQ，又∵PC∥x轴，∴四边形POQC是平行四边形，∴∠OPC=∠AQC．（3）解：①在Rt△COQ中，OC=3，OQ=4，由勾股定理得：CQ=5．如答图1所示，过点N作ND⊥x轴于点D，则ND∥OC，∴△QND∽△QCO，∴，即，解得：ND=3﹣t．设S=S△AMN，则：S=AM•ND=•3t•（3﹣t）=﹣（x﹣）2+．又∵AQ=7，∴点M到达终点的时间为t=，∴S=﹣（x﹣）2+（0＜t≤）．∵﹣＜0，＜，且x＜时，y随x的增大而增大，∴当t=时，△AMN的面积最大．②假设直线PQ能够垂直平分线段MN，则有QM=QN，且PQ⊥MN，PQ平分∠AQC．由QM=QN，得：7﹣3t=5﹣t，解得t=1．此时点M与点O重合，如答图2所示：设PQ与OC交于点E，由（2）可知，四边形POQC是平行四边形，∴OE=CE．∵点E到CQ的距离小于CE，∴点E到CQ的距离小于OE，而OE⊥x轴，∴PQ不是∠AQC的平分线，这与假设矛盾．∴直线PQ不能垂直平分线段MN．24．（14分）（2012•海南）如图，顶点为P（4，﹣4）的二次函数图象经过原点（0，0），点A在该图象上，OA交其对称轴l于点M，点M、N关于点P对称，连接AN、ON，（1）求该二次函数的关系式；（2）若点A在对称轴l右侧的二次函数图象上运动时，请解答下面问题：①证明：∠ANM=∠ONM；②△ANO能否为直角三角形？如果能，请求出所有符合条件的点A的坐标；如果不能，请说明理由．解：（1）∵二次函数的顶点坐标为（4，﹣4），∴设二次函数的解析式为y=a（x﹣4）2﹣4，又二次函数过（0，0），∴0=a（0﹣4）2﹣4，解得：a=，∴二次函数解析式为y=（x﹣4）2﹣4=x2﹣2x；（2）①证明：过A作AH⊥l于H，l与x轴交于点D，如图所示：设A（m，m2﹣2m），又O（0，0），∴直线AO的解析式为y=x=（m﹣2）x，则M（4，m﹣8），N（4，﹣m），H（4，m2﹣2m），∴OD=4，ND=m，HA=m﹣4，NH=ND﹣HD=m2﹣m，在Rt△OND中，tan∠ONM==，在Rt△ANH中，tan∠ANM====，∴tan∠ONM=tan∠ANM，则∠ANM=∠ONM；②△ANO能为直角三角形，理由如下：分三种情况考虑：（i）若∠ONA为直角，由①得：∠ANM=∠ONM=45°，∴△AHN为等腰直角三角形，∴HA=NH，即m﹣4=m2﹣m，整理得：m2﹣8m+16=0，即（m﹣4）2=0，解得：m=4，此时点A与点P重合，不存在A点使△ONA 为直角三角形；（ii）若∠AON为直角，根据勾股定理得：OA2+ON2=AN2，∵OA2=m2+（m2﹣2m）2，ON2=42+m2，AN2=（m ﹣4）2+（m2﹣2m+m）2，∴m2+（m2﹣2m）2+42+m2=（m﹣4）2+（m2﹣2m+m）2，整理得：m（m2﹣8m-16）=0，解得：m=0（不合题意，去掉），或m=4+4√2 ，此时A点坐标为（4+4√2，4），（iii）若∠NAO为直角，可得∠NAM=∠ODM=90°，且∠AMN=∠DMO，∴△AMN∽△DMO，又∠MAN=∠ODN=90°，且∠ANM=∠OND，∴△AMN∽△DON，∴△AMN∽△DMO∽△DON，∴=，即=，整理得：（m﹣4）2=0，解得：m=4，此时A与P重合，∠NAO不能为直角，综上，点A在对称轴l右侧的二次函数图象上运动时，可得△ANO能为直角三角形，点A的坐标为(4+4√2 ，4)②△ANO能为直角三角形.分三种情况讨论：Ⅰ）若∠ANO=90°，由①则有∠RNO=45°则RN=RO=4，即点A、M、N、P重合此时OA与ON重合，△ANO不存在，所以∠ANO不能等于90°Ⅱ）若∠AON=90°，连结OP则有OP=PN=PM，OP=∵PN=t-4 ∴=t-4 ∴t=4+∴A(4+ ，4)，即此时△ANO是直角三角形Ⅲ）若∠OAN=90°，连结AP则AP=PM=PN=t-4，由于AQ= t-4 则AP=AQ而∠AQP=90°，AP≠AQ相矛盾∴∠OAN不能等于90°综上所述，可得△ANO能为直角三角形，点A的坐标为(4+4√2 ，4)24．（14分）（2011•海南）如图，已知抛物线y=﹣x2+bx+9﹣b2（b为常数）经过坐标原点O，且与x轴交于另一点E．其顶点M在第一象限．（1）求该抛物线所对应的函数关系式；（2）设点A是该抛物线上位于x轴上方，且在其对称轴左侧的一个动点；过点A作x轴的平行线交该抛物线于另一点D，再作AB⊥x轴于点B．DE⊥x轴于点C．①当线段AB、BC的长都是整数个单位长度时，求矩形ABCD的周长；②求矩形ABCD的周长的最大值，并写出此时点A的坐标；③当矩形ABCD的周长取得最大值时，它的面积是否也同时取得最大值？请判断井说明理由．解：（1）由题意代入原点到二次函数式则9﹣b2=0，解得b=±3，由题意抛物线的对称轴大于0，，所以b=3，所以解析式为y=﹣x 2+3x ；（2）①y= -x²+3x = -(x- 3/2)² + 9/4 M(0,9/4)AB 为整数，∴AB=1,或2 当AB=1 时，BC 不是整数 故AB=2，易求得BC=2 ∴周长为 6②设B(m,0) A(m,-m²+3m) 则C(3-m,0)周长=(-m²+3m+3-2m)*2= -2m²+2m+6= -2(m-1/2)² +13/2 m=1/2时，最大值 13/2 此时A(1/2，5/4)③面积=(-m²+3m)(3-2m) m=1/2时，面积= 5/2而当m=3/5时，面积= 324/125 > 5/2 所以周长最大时面积不是最大24．（14分）（2010•海南）如图11，在平面直角坐标系中，直线3+-=x y 与x 轴、y 轴分别交于点B 、C ；抛物线cbx x y ++-=2经过B 、C 两点，并与x 轴交于另一点A ．（1）求该抛物线所对应的函数关系式； （2）设)(y x P ，是（1）所得抛物线上的一个动点，过点P 作直线x l ⊥轴于点M ，交直线BC 于点N ．① 若点P 在第一象限内．试问：线段PN 的长度是否存在最大值 ？若存在，求出它的最大值及此时x 的值；若不存在，请说明理由；② 求以BC 为底边的等腰△BPC 的面积24．（1）由于直线3+-=x y 经过B C 两点,令y =0得x =3；令x =0，得y =3∴B （3，0），C （0，3）……1分∵点B 、C 在抛物线c bx x y ++-=2上，于是得93b+c=0c=3-+⎧⎨⎩……2分 解得b=2，c=3……3分∴所求函数关系式为322++-=x xy ……4分（2）①∵点P （x ,y ）在抛物线322++-=x x y 上，且PN ⊥x 轴，∴设点P 的坐标为（x , 322++-x x） ……5分同理可设点N的坐标为（x ，3+-x ） ……6分又点P 在第一象限， ∴PN=PM-NM=（322++-x x ）-（3+-x =x x 32+=49)23(2+--x……7分∴当23=x 时， Oxy B A N CPlM图11BA CPOxylNM线段PN 的长度的最大值为49． ……8分 ②由题意知，点P 在线段BC 的垂直平分线上，又由①知，OB =OC∴BC 的中垂线同时也是∠BOC 的平分线， ∴设点P 的坐标为),(a a 又点P 在 抛 物 线 322++-=x x y 上,于是有322++-=a aa∴032=--a a……9分解得2131,213121-=+=a a……10分∴点P 的坐标为：()2131,2131++ 或 ()2131,2131-- (11)分若点P 的坐标为 ()2131,2131++ ，此时点P 在第一象限，在Rt △OMP 和Rt △BOC 中， 1132MP OM ==，OB=OC=3BOC BOCP S ∆∆-=四边形S S BPCBOP BOC =2S S ∆∆- 11=2BO PM-BO CO 22⨯⋅⋅⋅ 11139=2322+⨯⨯- 3136-若点P 的坐标为 ， 此时点 (12)()2131,2131--OxyNlMPCABPP在第三象限， 则BOCCOP BOP BPCS S S S∆∆∆∆++=111313233222-=⨯+⨯⨯ 113193222-=⨯+313392+=31362=……13分。

[中考12年]海南省2001-2012年中考数学试题分类解析专题2：代数式和因式分解一、选择题1. （2001年海南省3分）下列运算正确．．的是【】．A．x3＋x3＝2x6 B．x·x2＝x3C．（－x3）2＝－x6 D．x6÷x3＝x22. （2001年海南省3分）（a－b）2＝【】．A．a2－b2B．a2＋b2C．a2－ab＋b2D．a2－2ab＋b2【答案】D。

【考点】完全平方公式。

【分析】直接根据完全平方公式得出结论：（a－b）2＝a2－2ab＋b2。

故选D。

3. （2001年海南省3分）某商场在统计今年第一季度的销售额时发现，二月份比一月份增加10%，三月份比二月份减少10%，则三月份的销售额比一月份的销售额【】．A．增加10% B．减少10% C．不增也不减D．减少1%4. （2002年海南省3分）下列运算中正确的是【】A．x2+x2=x2 B．x•x4=x4 C．（xy）4=xy4 D．x6÷x2=x4【答案】D。

【考点】合并同类项，同底幂乘法和除法，积的乘方。

【分析】根据合并同类项，同底幂乘法和除法，积的乘方运算法则逐一计算作出判断：A 、应为x 2+x 2=2x 2，故本选项错误；B 、应为x•x 4=x 5，故本选项错误；C 、应为（xy ）4=x 4y 4，故本选项错误； D 、x 6÷x 2=x 4，故本选项正确。

故选D 。

5.（2002年海南省3分）下列因式分解中，错误的是【 】A ．()()219x 13x 13x -=+-B ．2211a a (a )42-+=-C ．()mx my m x y -+=-+D ．()()ax ay bx by x y a b --+=--6. （2003年海南省2分）下列各式中，不一定成立的是【 】A ．222a b a 2ab b +=++（）B ．222b a a 2ab b -=-+（）C ．()()22a b a b a b +-=-D ．222a b a b -=-（）【答案】D 。

海南省2010年初中毕业生学业考试数学科分析报告孙孝武（海南省教育研究培训院）邓之淮（海南省文昌中学）初中毕业生数学学业考试（以下简称为数学学业考试）是义务教育阶段数学科的终结性考试，其目的是全面、准确地评估初中毕业生达到《全日制义务教育数学课程标准（实验稿）》（以下简称为《课程标准》）所规定的数学学业水平的程度，同时又为高中阶段学校选拔招生提供重要的依据。

2010年我省共有123088名初中毕业生，其中参加中考人数121183人，缺考1905人，现根据中考的实际情况分析如下。

一、命题依据数学科考试命题以《课程标准》为基本依据，以《海南省2010年新课程初中学业考试数学科考试说明》作为指导，结合海南省2010年初中毕业生实际情况，体现考试的基础性、公平性，保证科学、有效，坚持平稳过渡，稳中有变。

数学科考试命题的指导思想是：（1）数学学业考试要有利于引导和促进数学教学全面落实《课程标准》所设立的课程目标，有利于引导改善学生的数学学习方式，提高学生数学学习的效率，有利于高中阶段学校综合、有效地评价学生的数学学习状况；（2）数学学业考试重视对双基过程和结果的评价，又要重视对学生在数学思考能力和解决问题能力方面发展状况的评价，重视对学生的数学认识水平的评价；（3）数学学业考试面向全体学生，公正、客观、全面、准确地评价学生，力求不同的学生在数学上有不同的发展，实现《课程标准》的评价理念。

二、试题点评1．试题结构我省初中毕业生学业考试数学科考试采用闭卷、笔试的方式。

考生可以带计算器及规定的作图工具进入考场。

考试时间为100分钟，满分为100分，超量满分为110分。

全省统一采用电脑阅卷。

按照教育部评价改革的要求，考试成绩采试题有选择题、填空题和解答题三大题型，分值比例约为2:1:3。

其中，“数与代数”、“空间与图形”、“统计与概率”三个知识领域分值比例约为4:4:2。

今年试题结构与去年的一致，选择题有12道，每题的分值为3分，填空题有6道，每题的分值为3分，解答题的题量不变，分值为56分。

2010海南省中考数学试题及答案海南省2010年初中毕业学业考试数学科试题一、选择题（本大题满分36分，每小题3分）1．－2的绝对值等于（ ）A ．－2B ．－ 1 2C ． 12D ．22．计算－a －a 的结果是（ ）A ．0B ．2aC ．－2aD ．a 23．在平面直角坐标系中，点P (2，3)在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 4．如图所示几何体的主视图是（ ）5．同一平面内，半径是2cm 和3cm 的两圆的圆心距为5cm ，则它们的位置关系是（ ） A ．相离 B ．相交 C ．外切 D ．内切6．若分式 1x －1有意义，则x 的取值范围是（ ）A ．x ＞1B ．x ＜1C ．xA B CDA B D A B CD O ≠1 D ．x ≠07．如图，a 、b 、c 分别表示△ABC 的三边长，则下面与△ABC 一定全等的三角形是（ ）8．方程3x －1＝0的根是（ ）A ．3B ． 1 3C ．－ 13 D ．－39．在正方形网格中，∠α的位置如图所示，则tan α的值是（ ）A ．33B ．53C ． 12D ．210．如图，在梯形ABCD 中，AD ∥BC ，AC 与BD 相交于点O ， 则下列三角形中，与△BOC 一定相似的是（ ）A ．△ABDB ．△DOAC ．△ACD D ．△ABO 11．如图，在△ABC 中，AB ＝AC ，AD ⊥BC 于点D ，B a c b 72°50aa b b b50°50°50°58°72°ABCD α的平分线交AD于点E ，则DE ＝ cm ．18．如图，将半径为4cm 的圆形纸片折叠后，圆弧恰好经过圆心O ，则折痕AB 的长度为 cm ．三、解答题（本大题满分56分）19．（每小题4分，满分8分）(1)计算：10―(― 13)×32；(2)解方程： 1x －1－1＝0．20．(8分)从相关部门获悉，2010年海南省高考报名人数共54741人，下图是报名考生分类统计图．2010年海南省高考报名考生分类条形统计图2010年海南省高考报名考生分类扇形统计图根据以上信息，解答下列问题：(1)2010年海南省高考报名人数中，理工类考生___________人；(2)请补充完整图中的条形统计图和扇形统计图(百分率精确到0.1%)；(3)假如你绘制图中扇形统计图，你认为文史类考生对应的扇形圆心角应为°(精确到1°)．21．(8分)如图，在正方形网格中，△ABC的三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题：(1)将△ABC向右平移5个单位长度，画出平移后的△A1B1C1；(2)画出△ABC关于x(3)将△ABC绕原点O后的△A3B3C3；(4)在△A1B1C1、△A2△________与△△________与△22．(8分)2010年上海世博会入园门票有11种之多，其中“指定日普通票”价格为200元一张，“指定日优惠票”价格为120元一张，某门票销售点在5月1日开幕式这一天共售出这两种门票1200张，收入216000元，该销售点这天分别售出这两种门票多少张？A E BC DF GH23．(11分)如图，四边形ABCD 和四边形AEFG 均为正方形，连接BG 与DE 相交于点H ．(1)证明：△ABG ≌△ADE ；(2)试猜想∠BHD 的度数，并说明理由； (3)将图中正方形ABCD 绕点A 逆时针旋转(0°＜∠BAE ＜180°)，设△ABE 的面积为S 1，△ADG 的面积为S 2，判断S 1与S 2的大小关系，并给予证明．24．(13分)如图，在平面直角坐标系中，直线y ＝－x＋3与x轴、y轴分别交于点B、C；抛物线y＝－x2＋bx＋c经过B、C两点，并与x轴交于另一点A．(1)求该抛物线所对应的函数关系式；(2)设P(x，y)是(1)所得抛物线上的一个动点，过点P作直线l⊥x轴于点M，交直线BC于点N．①若点P在第一象限内．在，请说明理由；②求以BC为底边的等腰△BPC的面积．海南省2010年初中毕业生学业考试数学课时题参考答案一、选择题(每小题3分，共36分)1． Ｄ ２．Ｃ ３．Ａ ４．Ａ ５．Ｃ ６．Ｃ ７．Ｂ ８．Ｂ ９．Ｄ １0．Ｂ 11．Ａ 12．Ｄ 二、填空题(每小题3分，共18分)13、14、 15、 16、 17、６ 18、34 a605a 91062.4 41三、解答题(共56分) 19．(1)原式＝10-(- )×9 ……1分 ＝10-(-3) ……2分 ＝10+3 ……3分 ＝13 ……4分 (2)两边都乘以)1(-x 得：1-)1(-x ＝0 ……1分 1-1+x ＝0 ……2分x＝2 ……3分检验：当x ＝2时入1-x ≠0，所以原方程的根是x ＝2． ……4分 20．2010年海南省高考报名考生分类条形统计图2010年海南省高考报名考生分类扇形统计图31解：(1)33510 ……3分(2)如图所示……7分(3)123 ……8分21．(1)△111C B A……2分(2)△222C BA……4分(3)△333C B A……6分(4)△222C BA、△333C B A；△111C B A、△333C B A……8分22．解法一：设该销售点这天售出“指定日普通票x张” ，“指定日优惠票”y 张，依题意得 ……1分⎩⎨⎧=+=+2160001202001200y x y x ……5分解得⎩⎨⎧==300900y x ……7分答：这天售出“指定日普通票900张” ，“指定日优惠票”300张． ……8分解法二：设该销售点这天售出“指定日普通票x 张”，则“指定日优惠票”销售了(1200-x )张，依题意得 ……1分 200x +120(1200-x )＝216000 ……5分 解得x ＝900 ∴1200-x ＝300 ……7分答：这天售出“指定日普通票”900张 ，“指定日优惠票”300张 ． ……8分 23．(1)证法一：证明：在正方形ABC D 和正方形A EFG 中 ∠G A E ＝∠BA D ＝90° ……1分 ∠G A E+∠E AB ＝∠BA D+E AB即∠G AB ＝∠E A D (2)分又A G ＝A E AB ＝A D∴△AB G ≌△A DE ……4分 证法二：证明：因为四边形ABC D 与四边形A EFG 都是正方形，所以∠G A E ＝∠BA D ＝90°，A G ＝A E ，AB ＝A D ，所以△E A D 可以看成是△G AB 逆时针旋转90°得到， 所以△AB G ≌△A DE (2)证法一：我猜想∠B HD ＝90°理由如下： ∵△AB G ≌△A DE ∴∠1＝∠2 ……5分而∠3＝∠4 ∴∠1+∠3＝∠2+∠4∵∠2+∠4＝90 ∠1+∠3＝90° ……6分 ∴∠B HD ＝90° ……7分 证法二：我猜想∠B HD ＝90°理由如下：由(1)证法(二)可知△E A D 可以看成是△G AB 逆时针旋转90°得到，B G 与DE 是一组对应边，CAB D E G F M N 图aＨ 1324所以B G ⊥DE ，即∠B HD ＝90° (3)证法一：当正方形ABC D 绕点A 逆时针旋转 0°＜∠BA E ＜180°时,S1和S2总保持相等． ……8分证明如下：由于0°＜∠BA E ＜180°因此分三种情况：①当0°＜∠BA E ＜90°时 (如图a ) 过点B 作B M ⊥直线A E 于点M ， 过点D 作DN ⊥直线A G 于点N ． ∵∠M A N ＝∠BA D ＝90° ∴∠M AB ＝∠N A D又∠A M B ＝∠A ND ＝90° AB ＝A D ∴△A M B ≌△A ND ∴B M ＝DN 又A E ＝A G ∴DN AG 21BM AE 21⋅=⋅∴21S S= ……９分②当∠BA E ＝90°时 如图b ∵A E ＝A G ∠BA E ＝∠D A G ＝90°AB ＝A D∴△AB E ≌△A DG ∴21S S = ……１０分ABC D E F G 图b③当90°＜∠BA E ＜180°时 如图c和①一样；同理可证21S S =综上所述，在(3)的条件下，总有21S S =．……11分 证法二：①当0°＜∠BA E ＜90°时，如图d 作EM ⊥AB 于点M ，作GN ⊥A D 交D A 延长线于点N ，则∠GN A ＝∠EM A ＝90°又∵四边形ABC D 与 四边形A EFG 都是正方形， ∴A G ＝A E ，AB ＝A D∴∠G A N+∠E A N ＝90°， ∠E A M+∠E A N ＝90° ∴∠G A N ＝∠E A M∴△G A N ≌△E A M (AA S )∴GN ＝EM ∵ABCDEF G 图c A B D E G F 图dＨM N C12ADG S AD GN ∆=⋅∴21S S=②③同证法一类似24．(1)由于直线3+-=x y 经过B 、C 两点, 令y ＝0得x ＝3；令x ＝0，得y ＝3 ∴B (3，0)，C (0，3) ……1分 ∵点B 、C 在抛物线cbx x y ++-=2上，于是得93b+c=0 c=3-+⎧⎨⎩ ……2分解得b ＝2，c ＝3 ……3分 ∴所求函数关系式为322++-=x x y ……4分(2)①∵点P (x,y )在抛物线322++-=x x y 上，且P N ⊥x 轴， ∴设点P 的坐标为(x , 322++-x x ) ……5分同理可设点N 的坐标为(x ，3+-x ) ……6分又点P 在第一象限， ∴P N ＝P M-NM ＝(322++-x x )-＝xx32+12ABE S AB EM ∆=⋅ADGABES S ∆∆=＝49)23(2+--x……7分 ∴当23=x 时，线段P N 的长度的最大值为49． ……8分②解法一：由题意知，点P 在线段BC 的垂直平分线上， 又由①知，O B ＝O C∴BC 的中垂线同时也是∠B O C 的平分线，∴设点P 的坐标为),(a a 又点P 在抛物线322++-=x x y 上,于是有322++-=a a a∴032=--a a……9分解得2131,213121-=+=a a ……10分∴点P 的坐标为：()2131,2131++ 或()2131,2131-- …11分若点P 的坐标为()2131,2131++ ，此时点P 在第一象限，在Rt △OM P 和Rt △B O C 中，MP OM ==O B ＝O C ＝3BOCBOCP S ∆∆-=四边形S S BPCBOP BOC=2S S ∆∆- 11=2BO PM-BO CO22⨯⋅⋅⋅19=2322⨯⨯若点P 的坐标为 ， 此时点P 在第三象限， 则BOCCOP BOP BPCS S S S∆∆∆∆++=11323322=⨯+⨯⨯193222=⨯+==……13分解法二：由题意知，点P 在线段BC 的垂直平分线上，又由①知，O B ＝O C∴BC 的中垂线同时也是∠B O C 的平分线， ∴设点P 的坐标为(),a a 又点P 在抛物线322++-=x x y 上，于是有322++-=a aa∴032=--a a……9分解得2131,213121-=+=a a ……10分 (12)()2131,2131--∴点P 的坐标为: ()2131,2131++ 或 ()2131,2131--…11分若点P 的坐标为()，此时点P 在第一象限，在Rt △OM P 和Rt △B O C 中，MP OM ==，O B ＝O C ＝3BOC BMP COMP S S ∆∆∆-+=梯形S S BPC()111222OC MP MO BM PM BO CO =+⋅+⋅-⋅ ＝＝ 点P 的坐标为()2131,2131-- ， 此时点P 在第三象限，(与解法一相同) ……13分33212131213132121312131321⨯⨯-+⋅⎪⎪⎭⎫ ⎝⎛+-++⋅⎪⎪⎭⎫ ⎝⎛++26133- (12)。

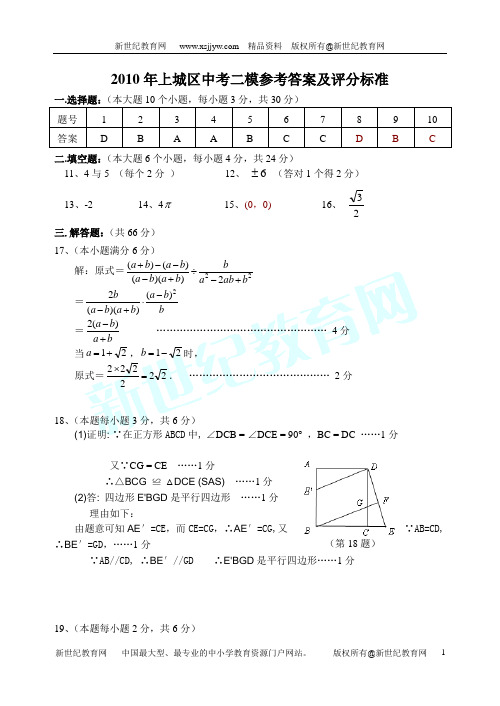
（第18题）2010年上城区中考二模参考答案及评分标准二.填空题：（本大题6个小题，每小题4分，共24分）11、4与5 （每个2分 ） 12、 6± （答对1个得2分） 13、-2 14、4π 15、(0，0) 16、 23 三.解答题：（共66分）17、（本小题满分6分）解：原式＝222))(()()(b ab a bb a b a b a b a +-÷+---+＝b b a b a b a b 2)())((2-⋅+-＝ba b a +-)(2 …………………………………………… 4分当21+=a ，21-=b 时，原式＝222222=⨯． …………………………………… 2分18、（本题每小题3分，共6分）(1)证明: ∵在正方形ABCD 中, ∠DCB = ∠DCE = 90° ，BC = DC ……1分又∵CG = CE ……1分∴△BCG ≌ △DCE (SAS) ……1分 (2)答: 四边形E'BGD 是平行四边形 ……1分 理由如下：由题意可知AE ′=CE ，而CE=CG ，∴AE ′=CG,又∵AB=CD,∴BE ′=GD ，……1分∵AB//CD, ∴BE ′//GD ∴E'BGD 是平行四边形……1分19、（本题每小题2分，共6分）解：（1）解：33630024973÷=++++(名) ……1分答:本次调查共抽测了300名学生. ……1分 （2）中位数在第三小组. ……1分∵这300个数据的中位数是从小到大排列后的第150和第151个数的平均数，而第150和第151个数位于第三小组. ∴中位数在第三小组. ……1分 （3）∵视力在4.9—5.1范围内的人有84人.84300008400300⨯=（人） ……1分 答：全市初中生视力正常的约有8400人. ……1分 20.（本题每小题4分，共8分） （1）方案正确 ……4分 (2)方案正确 ……4分21.（本题每小题4分，共8分） 解：（1）设与之间的函数关系式为……………1分∵经过（60，400）（70，300）∴ ……………1分① ② ③ ④⑤⑥ 中点中点中点中点①③②⑥④⑤解得： ……………1分∴与之间的函数关系式为 …………1分（2）P ＝（－10x ＋1000）（x －50），∴P 与x 之间的函数关系式为210150050000p x x =-+- ………2分 P ＝∴当x ＝75时，P 最大，最大利润为6250元 ……………2分22、（本小题满分10分） （1）①②③ ………3分 （2）证明①或②或③………7分23、（本小题满分10分） 解：分两种情况：(1)如图1，在Rt△BD C 中，∠B=30o在Rt△CDP 中，∠CPD=60o，DP=CD tan ∠CPD =3320在Rt△ADC 中，AD=DC=20AP=AD+DP=(20+3320)千米………5分（草图画对1分，计算正确4分） (2)如图2，同(1)可求得DP=3320，AD=20 AP=AD-DP=(20-3320)千米 ……4分（草图画对1分，计算正确3分） 故交叉口P 与加油站A 的距离为(20±3320)千米． ……1分 图1图2B24．（本题每小题4分，共12分）解：(1)OA=2，OB=4 …………………………………………1分 点C 是线段AB 的中点，OC=AC作CE ⊥x 轴于点E ．……………………………1分 ∴ OE=12OA=1，CE=12OB=2．∴ 点C 的坐标为(1，2) …………………………………2分(2)作DF ⊥x 轴于点F△OFD∽△OEC，OD OC =23，于是可求得OF=32，DF=34．∴ 点D 的坐标为(32，34) …………………………………1分 设直线AD 的解析式为y=kx+b ．把A(2，0)，D(32，34)分别代人，得⎪⎩⎪⎨⎧=+=+343202b k b k ……………1分 解得 ⎩⎨⎧=-=21b k ……………………………1分∴ 直线AD 的解析式为y=-x+2 ……………………………1分 (3)存在．(每个点得1分，共4分)Q 1(-2，2)…………1分 Q 2(2，-2) ………………………1分 Q 3(1，-1) …………1分 Q 4(2，2) ………………………1分说明：学生有不同的解题方法，只要正确，均可参照本评分标准，酌情给分．。

数学 第1页（共4页)海口市2010年初中毕业生学业模拟考试（一）数学科试题（考试时间100分钟，满分110分）特别提醒：1．选择题用2B 铅笔填涂，其余答案一律用黑色笔填写在答题卡上,写在试题卷上无效. 2. 答题前请认真阅读试题及有关说明. 3．请合理安排好答题时间.一、选择题（本大题满分36分，每小题3分）在下列各题的四个备选答案中，只有一个是正确的，请在答题卡上把你认为正确的答案的字母代号按要求．．．用2B 铅笔涂黑. 1. -6的相反数是A. -6B. 6C.61D. 61-2. 数据2500000用科学记数法表示为A. 25×105B. 2.5×105C. 2.5×106D. 2.5×1073．函数x y -=4中，自变量x 的取值范围是A. x ≠4B. x ≥4C. x ＜4D. x ≤44. 图1是由5个大小相同的小正方体摆成的立体图形，它的俯视图．．．是5．若分式211x x --的值为0，则x 的值是A ．x =1B ．x =-1C ．x =±1D ．x ≠16．若点A 在直线y =x -1上，则点A 的坐标是 A ．（-1，0）B ．（0，1）C ．（1，0）D ．（1，-1）7．在△ABC 中，∠C =90°，若sin A =53，则cot A 等于A ．B.C.D.图1正面数学 第2页（共4页)A ．34B ．43C ．35D ．548. 一组数据3，-2，1，3，0，-1的中位数和众数分别是A ．0，3B ．0.5，3C ．2，3D ．3，1 9．如图2，在4×4的正方形网格中，∠1、∠2、∠3的大小关系是A ．∠1＞∠2＞∠3B ．∠1=∠2=∠3C ．∠1＜∠2=∠3D ．∠1=∠2＞∠3 10．如图3，在△ABC 中，D 、E 分别是AB 、AC 的中点，则S △ADE :S 四边形BCED 等于A ． 1:2B ．1:3C ．1:4D ． 2:311．如图4，在⊙O 中，，直径CD ⊥AB 于E ，则∠BDC 等于A ．40°B ．50°C ．60°D ．70°12. 某超市一月份的营业额为200万元，三月份的营业额为288万元，若每月比上月增长的百分率相同，则这个增长的百分率是 A. 10%B. 15%C. 18%D. 20%二、填空题（本大题满分18分，每小题3分） 13. 计算：-3a 2-a 2= .14．不等式组⎩⎨⎧>+<-4)5(201x x 的解集是 ． 15．从长度为2，3，5，7的四条线段中随机选取三条，这三条线段能构成三角形的概率是 ．16. 如图5，矩形ABOC 的面积为6，若反比例函数xky =（x ＜0）的图象经过点A ，则该反比例函数的关系式为 .17．如图6，在梯形ABCD 中，AD ∥BC ， AB =DC ，∠A =120°，BC =2．将该梯形沿对角线BD 折叠，点A 恰好落在BC 边上的E 处，则梯形ABCD 的周长为 ．1 图223D E OABC图4 AB POC图7图5ABC E (A )D图6ABCD图3E数学 第3页（共4页)18．如图7，AB 是⊙O 的直径，AC 是弦，AB =5，∠A =30°，P 是AB 延长线上一动点，要使直线PC 与⊙O 相切，则BP 的长等于 . 三、解答题（本大题满分56分） 19.（本题满分8分，每小题4分）（1）计算: (-2)3-(2-5)+12×(-3)；（2）化简：41221122-++÷⎪⎭⎫ ⎝⎛+-x x x x . 20.（本题满分8分）一辆汽车从A 地驶往B 地，前31路段为普通公路，其余路段为高速公路．已知汽车在普通公路上行驶的速度为60km/h ，在高速公路上行驶的速度为100km/h ，汽车从A 地到B 地一共行驶了2.2h ．求汽车在普通公路和高速公路上行驶的时间各是多少？21.（本题满分8分）某校学生会准备调查本校九年级学生每天（除课间操外）课外锻炼的平均时间．（1）确定调查方式时，①甲同学说：“我到1班调查全体同学”；②乙同学说：“我到学校操场询问参加锻炼的同学”；③丙同学说：“我到九年级每个班随机调查一定数量的同学”. 以上同学说的三种调查方式中最为合理的是 （填写序号）； （2）他们采用了最为合理的调查方式收集数据，并绘制出如图8.1所示的条形统计图和如图8.2所示的扇形统计图，请将图8.1补充完整,并标出人数；（3）若该校九年级共有240名学生，则其中每天（除课间操外）课外锻炼平均时间不超过20分钟的人数为 人. (注：图8.2中相邻两虚线形成的圆心角为30°)22.（本题满分8分）如图9所示的正方形网格中，△ABC 和△A 1B 1C 1的顶点均在格点上，在所给的平面直角坐标系中解答下列问题： （1）作出△ABC 绕A 点按逆时针方向旋转90°后得到的△AB 2C 2；图940分钟20分钟图8.2人数10分钟 20分钟40分钟 基本 不参加锻炼时间图8.15 10 15 20 25 30 35 40 0数学 第4页（共4（2）△AB 2C 2与△A 1B 1C1满足什么几何变换（直接写答案），设P 2(a ,b )为△AB 2C 2边上任一点， 写出上述变换中P 2点的对应点P1的坐标； （3）经过什么样的图形变换，可以把△ABC 变换得到△A 1B 1C 1，写出简要的文字说明.23.（本题满分10分）如图10.1，在△ABC 中，AB =AC ，∠BAC =90°，D 为BC 边的中点，一等腰直角三角尺的直角顶点P 在BC 边上移动，两直角边分别与AB ，AC 交于E ，F 两点，且斜边MN ∥BC ． （1）求证：四边形PEAF 是矩形；（2）请你通过观察、测量，猜想写出线段DE 与DF 满足的数量关系及位置关系，然后证明你的结论；（3）当三角尺继续沿BC 方向平移到图10.2所示的位置时，点P 在线段BC 的延长线上，三角尺两直角边所在直线与△ABC 的两边BA ，AC 的延长线分别交于点E ，F ，请直接写出（2）中的两个结论是否仍然成立.24.（本题满分14分）如图11，已知抛物线经过点A (4,0)、B (3,2)、C (0,4)，BD ⊥y轴，垂足为D .（1）求点D 的坐标及该抛物线所对应的函数关系式；（2）点P 从点B 出发，沿折线B →D →C 以每秒1个单位的速度运动，过点P 作PE ⊥DB ，交该抛物线于E ，F 是x 轴上一动点，且tan ∠PF A=1. 设点P 的运动时间为t （秒），△PEF 的面积为S ① 求S 关于t 的函数关系式及自变量t ② 当t 为何值时，S ③ 在S 取得最大值时，判断以EF 四边形QEPF 的顶点Q 是否落在（1图11PD 图10.1数学 第5页（共4页)线上，并说明理由.海口市2010年初中毕业生学业模拟考试(一)数学科参考答案及评分标准一、B C D A B C A B D B C D 二、13. -4a 2 14. x ＞1 15.41 16．x y 6-= 17. 5 18. 2.5三、19．（1）原式=-8-(-3)+(-36 )…（2分） =-8+3-6 …（3分）=-11 …（4分）20．设汽车在普通公路上行驶了x h ，高速公路上行驶了y h ． ……………（1分）根据题意，得⎩⎨⎧=⨯=+.100260,2.2y x y x ………………………………（5分）解得 ⎩⎨⎧==2.11y x答：汽车在普通公路上行驶了1h ，高速公路上行驶了1.2h ．（8分）21．（1）③ ……………………(2分) （2）如图1所示 ……(5分) （3）220 …………………(8分)22．（1）如图2所示. 作图正确.…（2分） （2）关于点O 中心对称. P 1(-a ,-b ) …(5分)（3）答案不唯一. …(8分)如：答案1：先将△ABC 绕点A 逆时针旋转90°后， 得到的△AB 2C 2，然后再将△AB 2C 2绕点O旋转180°得到△A 1B 1C 1.（2）原式=12421222++-⋅+-+x x x x x …（2分） 2)1()2)(2(21+-+⋅++=x x x x x …（3分） 12+-=x x …（4分）图2人数 10分钟 20分钟 40分钟 基本 不参加 锻炼时间图15 10 15 20 25 30 35 40 0数学 第6页（共4答案2：先将△ABC 绕点B 顺时针旋转90°后， 再向右平移4个单位长度得到△A 1B 1C 1.答案3：先将△ABC 向右平移4个单位长度后， 再绕点B （B 1）顺时针旋转90°得到△A 1B 1C 1.23．（1）∵ AB =AC , ∠BAC=90°，△PMN 是等腰直角三角形,∴ ∠BAC =∠MPN =90°，∠N =∠C =45°， ∵ MN ∥BC ,∴ ∠FPC =∠N =45°,∴ ∠AFP =∠FPC +∠C =45°+45°=90°．∴ 四边形PEAF 是矩形. ………………………………（3分） （2）DE =DF ，DE ⊥DF . ………………………………（4分）如图3，连结AD∵ △ABC 是等腰直角三角形，D 为斜边BC 的中点，∴ AD =21BC =CD ，AD ⊥BC ，∠EAD =∠C =45°，∴ ∠ADC =90°.∵ ∠FPC =∠C =45°,∴ PF =CF ∵ 四边形PEAF 为矩形∴ PF =AE ,∴ AE =CF , ∴ △AED ≌△CFD , ∴ DE =DF ，∠ADE =∠CDF ． ………………………………（6分） ∴ ∠EDF =∠ADE +∠ADF =∠CDF +∠ADF =∠ADC =90°,∴ DE ⊥DF . ………………………………（8分） （3）（2）中的两个结论仍然成立. ………………………………（10分）(注：用其它方法求解参照以上标准给分.)24．（1）D (0,2). ………………………………（1分）依题意, 设所求抛物线的函数关系式为y =ax 2+bx +4,则 ⎩⎨⎧=++=++.2439,04416b a b a 解得⎪⎪⎩⎪⎪⎨⎧=-=3131b a ∴ 所求抛物线的函数关系式为y =-31x 2+31x +4. ………（4分）（2）① 分两种情况讨论：(Ⅰ)如图4，当0＜t ＜3时，点P 在线段BD 上运动，此时，DP =3-t .延长EG 交x 轴于点G ，则PG =2. ∵ tan ∠PF A =1，∴ FG =PG =2. D 图3数学 第7页（共4页)∴ EP =EG -PG =31-(3-t )2+31(3-t )+4-2 =-31t 2+35t . ∴ S =21EP •FG =21(t t 35312+-)×2=-31t 2+35t (0＜t ＜3). (Ⅱ) 如图5，当3≤t ＜5时，点P 在线段DC 此时，点E 与点C 重合，EP =5-t .∵ tan ∠PF A =1，∴ FO =PO =EO -EP =4-(5-t )=t -1.∴ S =21EP •FO =21(5-t )(t -1)=21-t 2+3t 25-(3≤t ＜5).…（9分）②(Ⅰ) 当0＜t ＜3时，S =t t 35312+-=1225)25(312+--t .∵ a ＜0, ∴ 当t =25时，S 最大=1225.（Ⅱ) 当3≤t ＜5时，S =21-t 2+3t 25-=21-(t -3)2+2.∵ a ＜0, ∴ 当t =3时，S 最大=2.综上所述，当t =25时，S 最大=1225. ……………………（11分）③ 如图6，当S 取得最大值时， 点P 、E 的坐标分别是(21,2)、(21,1249)，且PE =1225.∵ tan ∠PF A =1，∴ FG =PG =2,∴ FO =FG -OG =221-=23，∴ 点F (若四边形QEPF 是以EF 则Q 点坐标为(23-,1225).把x =23-代入431312++-=x x y ，得y ∵ 411≠1225,∴ 点Q 不在抛物线431312++-=x x y 上. …………………（14分）图6C D EF Q C D(注：用其它方法求解参照以上标准给分.)数学第8页（共4页)。

2010年海南省中考数学试卷参考答案与试题解析一、选择题（共12小题，每小题3分，满分36分）1．（3分）（2012•徐州）﹣2的绝对值是（）A．﹣2 B．﹣C．D．2【考点】M113 绝对值【难度】容易题【分析】计算绝对值要根据绝对值的定义,任何一个数的绝对值一定是非负数，∵﹣2＜0，∴|﹣2|=﹣（﹣2）=2．故选D．【解答】D．【点评】本题考查了绝对值的意义，任何一个数的绝对值一定是非负数，所以﹣2的绝对值是2．部分学生易混淆相反数、绝对值、倒数的意义，而错误的认为﹣2的绝对值是，而选择B．2．（3分）（2010•海南）计算﹣a﹣a的结果是（）A．0 B．2a C．﹣2a D．a2【考点】M11I 整式【难度】容易题【分析】根据合并同类项法则求解即﹣a﹣a=（﹣1﹣1）a=﹣2a，故选C．【解答】C．【点评】本题主要考查了合并同类项的法则，熟练掌握运算法则是解题的关键．注意：所含字母相同，且相同字母的指数也相同的项叫做同类项.将多项式中的同类项合并为一项，叫做合并同类项。

合并时，将系数相加，字母和字母指数不变就是合并同类项的法则3．（3分）（2010•海南）在平面直角坐标系中，点P（2，3）在（）A．第一象限 B．第二象限 C．第三象限 D．第四象限【考点】M137 不同位置的点的坐标的特征【难度】容易题【分析】点P（2，3）的横、纵坐标均为正，所以点P在第一象限，故选A．【解答】A．【点评】本题主要考查了平面直角坐标系中第二象限的点的坐标的符号特点．四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．4．（3分）（2010•海南）如图所示的几何体的主视图是（）A． B． C． D．【考点】M414 视图与投影【难度】中等题【分析】主视图是从几何体前面看所得到的图形即从前面看可得到左边有2个正方形，右边有1个正方形，所以选A．【解答】A．【点评】本题考查了三视图的知识，主视图是指从前面看所得到的图形，同时注意左视图、俯视图为分别从物体左方，上方看所得到的图形．5．（3分）（2010•海南）同一平面内，半径是2cm和3cm的两圆的圆心距为5cm，则它们的位置关系是（）A．相离 B．相交 C．外切 D．内切【考点】M34D 圆与圆的位置关系【难度】容易题【分析】由题意可得，圆心距等于两圆的半径之和，即可判断两圆的位置关系是外切．故选C【解答】C．【点评】本题主要是考查圆与圆的位置关系与数量关系间的联系．此类题为中考热点，需重点掌握．注意：圆心距用d来表示，两圆的半径分别用r,R来表示。

海南省海口市中考数学试卷及答案一、选择题(每小题3分。

共36分)在下列各题的四个备选答案中，只有一个是正确的．1．3的相反数是 ( )A ．-3B ．-31C ．3D ．31 2．计算2a-2(a+1)的结果是 ( )A ．-2B ．2C ．-1D ．13．在实数0、2 、-31、π中，无理数有 ( ) A ．1个 B ．2个 C ．3个 D ．4个4．如图，直线a 、b 被直线c 所截，且a ∥b ，若∠1=40°，则下列各式中，错误的是 ( )A ．∠2=40°B ．∠3=40°C ．∠4=40°D ．∠5=50°5．下列四个图形中，是轴对称图形的有 ( )A ．4个B ．3个C ．2个D ．1个6．如果双曲线y=xk 经过点(2，-3)，那么此双曲线也经过点 ( ) A ．(-3，-2) B ．(-3，2) C ．(2，3) D ．(-2，-3)7．如图，BC 是⊙O 的直径，A 是CB 延长线上一点，AD 切⊙O 于点D ，如果AB=2，∠A ：30'，那么AD 等于 ( )A ．2B ．3 c ．23 D ．228．下面四个图形均由六个相同的小正方形组成，其中是正方体表面展开图的是 ( )A ．B ． c ． D ．9．如果点A(m ，n)在第三象限，那么点B(0，m+n)在． ( )A ．x 轴正半轴上B ．x 轴负半轴上C ．y 轴正半轴上D ．y 轴负半轴上10．已知关于x 的方程x 2-(2m-1)x+m 2=O 有两个不相等的实数根，那么m 的最大整数值是( )A ．-2B ．-1C ．0D ．111．某天早晨，小明从家里出发，以v 1千米／时的速度前往学校，途中停留在一饮食店吃早餐，之后，又以v 2千米／时的速度向学校行进．已知V 1<V 2；那么能大致表示小明从家里到学校的时间t(小时)与路程s(千米)之间关系的图象是 ( )12．周长都是12cm 的正三角形、正方形、正六边形的面积S 3、S 4、S 6之间大小关系是 ( 。

新世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。

版权所有@新世纪教育网2010年海南省中考数学模拟试题（三）（本试题满分110分，考试时间100分钟）命题人：文昌中学 叶翠芳一、选择题（每小题给出的四个选项中，只有一个正确选项，请将正确选项的标号填入题后括号内．每小题3分，共36分）1．31-的倒数是（ B ） A.31 B.3 C.31- D.-3 2．据统计，海南省2009年财政总收入达到1580亿元，近似数1580亿精确到（ D ） A. 个位 B.十位 C. 千位 D. 亿位 3．下列计算中，结果正确的是（ D ）A.633a a a =+ B. 623a a a =⋅ C. 236a a a =÷ D. ()62342a a =-4．在函数5-=x x y 中，自变量x 的取值范围是( A )A ．5x ＞B ．5x ＜C ．5≥xD ．5≤x5．下图是由一些相同的小正方体构成的几何体的三视图，这些相同的小正方体的个数是（ B ） A.4个 B.5个 C.6个 D.7个6．某商场在“五一”期间推出购物摸奖活动，摸奖箱内有除颜色以外完全同的红色、白色与蓝色乒乓球，其中蓝色、白色乒乓球各有3个，红色乒乓球有2个，顾客摸奖时，如果摸到红色乒乓球，就中奖；否则就不中奖，那么顾客摸球一次就中奖的概率是( C ) A.21 B. 31 C. 41 D. 51 7．为了解某班学生一周的体育锻炼的时间，某综合实践活动小组对该班50名学生进行了调查，有关数据如下表：A．9小时和9小时 B. 9小时和8小时 C. 8.5小时和9小时 D.8.5小时和8小时8．为了鼓励节约用水，按以下规定收取水费：若每户每月用水量不超过20立方米，则每立方米水费2元，若每户每月用水量超过20立方米，则超过部分每立方米水费3元，设某户一个月所交水费为y （元），用水量为x （立方米），则y 与x 的函数关系用图象表示为（ A ）B C DA 主视图 左视图 俯视图新世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。

2010-2023历年高级中等学校招生全国统一考试数学卷（海南）第1卷一.参考题库(共20题)1.A，B两城相距600千米，甲、乙两车同时从A城出发驶向B城，甲车到达B城后立即返回．如图是它们离A城的距离y（千米）与行驶时间x（小时）之间的函数图象．（1）求甲车行驶过程中y与x之间的函数解析式，并写出自变量x的取值范围；（2）当它们行驶7了小时时，两车相遇，求乙车速度．2.如图，⊙O的直径CD⊥AB，∠AOC=50°，则∠CDB大小为(▲)A．25°B．30°D．50°3.如图1所示几何体的主视图是图1 A B C D4.-22的绝对值等于A．-22B．-C．D．225.如图1，Rt△ABC≌Rt△EDF，∠ACB=∠F=90°，∠A=∠E=30°．△EDF绕着边AB 的中点D旋转， DE，DF分别交线段AC于点M，K．（1）观察：①如图2、图3，当∠CDF="0°"或60°时，AM+CK_______MK(填“>”，“<”或“=”)．②如图4，当∠CDF="30°" 时，AM+CK___MK(只填“>”或“<”)．（2）猜想：如图1，当0°＜∠CDF＜60°时，AM+CK_______MK，证明你所得到的结论．（3）如果，请直接写出∠CDF的度数和的值．在梯形ABCD中，AD//BC，AC与BD相交于点O，则下列三角形中,与△BOC一定相似的是A．△ABDB．△DOAC．△ACDD．△ABO7.下列说法中正确的是(▲)A．“打开电视，正在播放《新闻联播》”是必然事件；B．某次抽奖活动中奖的概率为，说明每买100张奖券，一定有一次中奖；C．数据1，1，2，2，3的众数是3；D．想了解台州市城镇居民人均年收入水平，宜采用抽样调查．8.如图5，在△ABC中，AB=AC，AD⊥BC于点D，则下列结论不一定成立的是A．B．BD = CDC． 1 = 2D． B = C9.在反比例函数的图象的任一支上，都随的增大而增大，则的值可以是A．－1B．0C．1D．210.梯形ABCD中，AD∥BC，AB=CD=AD=2，∠B=60°，则下底BC的长是(▲) A．3B．4C．2D．2+211.同一平面内，半径分别是2cm和3cm的两圆的圆心距为5cm，则这两圆的位置关系是A．相离B．相交C．外切D．内切12.某种商品原价是120元，经两次降价后的价格是100元，求平均每次降价的百分率．设平均每次降价的百分率为，可列方程为▲．13.如图，△ABC中，∠C=90°，AC=3，点P是边BC上的动点，则AP长不可能是(▲)A．2.5B．3C．4D．514.下列立体图形中，侧面展开图是扇形的是(▲)15.一道选择题共有四个备选答案，其中只有一个是正确的，若有一位同学随意选了其中一个答案，那么他选中正确答案的概率是_________．16.类比学习：一动点沿着数轴向右平移3个单位，再向左平移2个单位，相当于向右平移1个单位．用实数加法表示为 3+（）=1．若坐标平面上的点作如下平移：沿x轴方向平移的数量为a（向右为正，向左为负，平移个单位），沿y轴方向平移的数量为b（向上为正，向下为负，平移个单位），则把有序数对{a，b}叫做这一平移的“平移量”；“平移量”{a，b}与“平移量”{c，d}的加法运算法则为．解决问题：（1）计算：{3，1}+{1，2}；{1，2}+{3，1}．（2）①动点P从坐标原点O出发，先按照“平移量”{3，1}平移到A，再按照“平移量”{1，2}平移到B；若先把动点P按照“平移量”{1，2}平移到C，再按照“平移量”{3，1}平移，最后的位置还是点B吗? 在图1中画出四边形OABC.②证明四边形OABC是平行四边形.（3）如图2，一艘船从码头O出发，先航行到湖心岛码头P（2，3），再从码头P航行到码头Q（5，5），最后回到出发点O.请用“平移量”加法算式表示它的航行过程．17.如图2，、、分别表示△ABC的三边长，则下面与△ABC一定全等的三角形是A B C D18.在平面直角坐标系中，点P（2，3）在A．第一象限B．第二象限C．第三象限D．第四象限19.反比例函数图象上有三个点，，，其中，则，，的大小关系是(▲)A．B．C．D．20.某工厂计划天生产60件产品，则平均每天生产该产品__________件．第1卷参考答案一.参考题库1.参考答案：（1）（2）（千米/小时）2.参考答案：A3.参考答案：A4.参考答案：D5.参考答案：（1）① =" " ②＞（2）略（3）6.参考答案：B解：∵AD//BC∴∠DAO=∠OCB,∠ADO=∠OBC∴△BOC∽△DOA7.参考答案：D8.参考答案：A解：∵AB=AC∴ B = C （等边对等角）BD = CD 1 =2（三线合一）只有△ABC是直角三角形时，AD = BD。